공간 데이터 베이스 - CNN(Continuous Nearest Neighbor)
CNN(Continuous Nearest Neighbor)
1. 개요
연속 최근접 이웃 쿼리는 쿼리 선분(query segment)을 따라 이동하면서 각 구간별로 가장 가까운 데이터 포인트를 찾는 문제이다. 목표는 데이터셋을 한 번만 순회하여 모든 분할 지점(split points)과 각 구간의 최근접 이웃을 찾는 것이다.
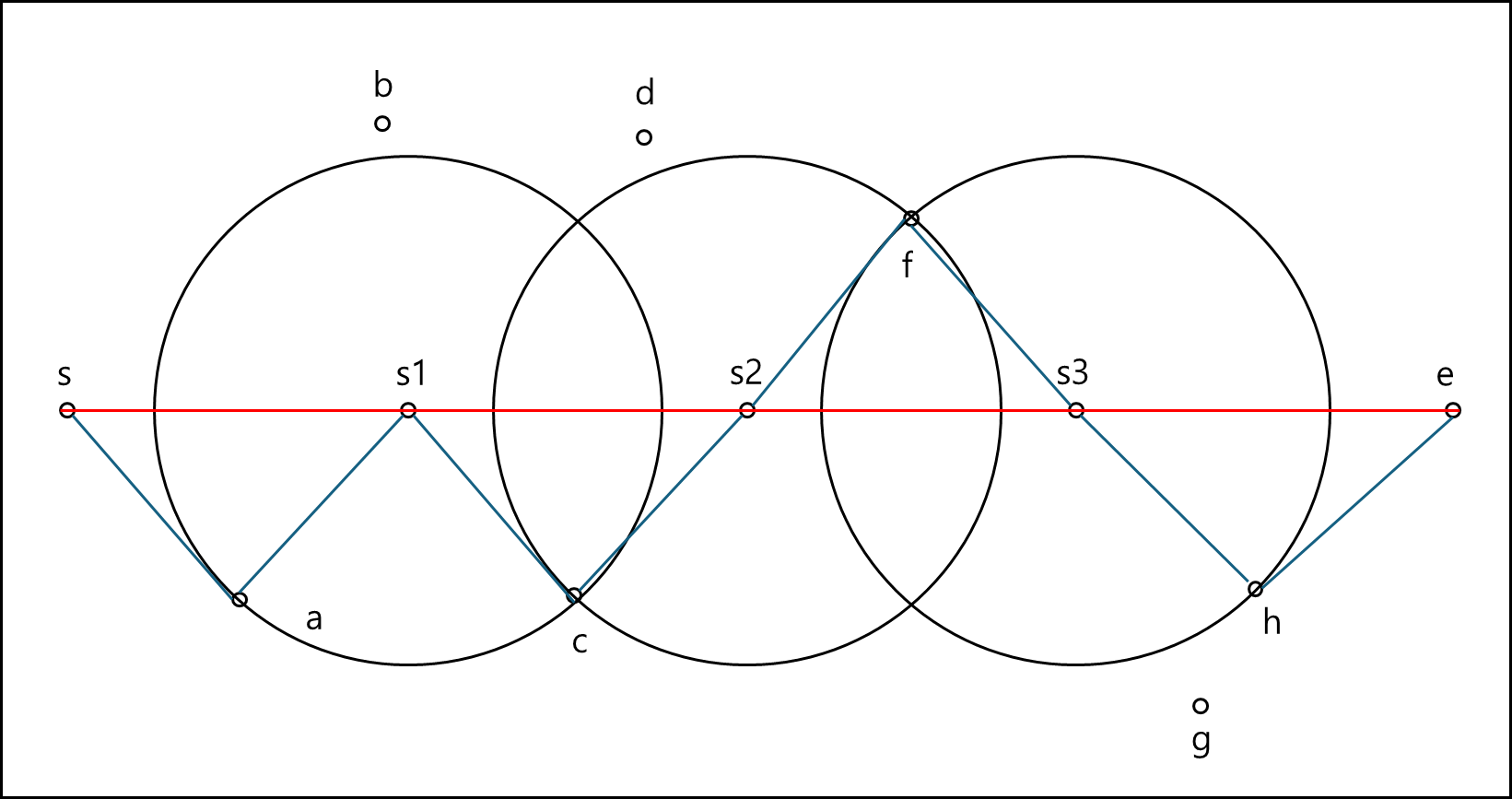
아래의 그림을 보자
s에서 e까지 이동한다고 할때 각각 a~h 에서 가장 가까운 점을 찾는 문제라고 생각하면 된다.
2. 핵심 부명제
1) Lemma 1
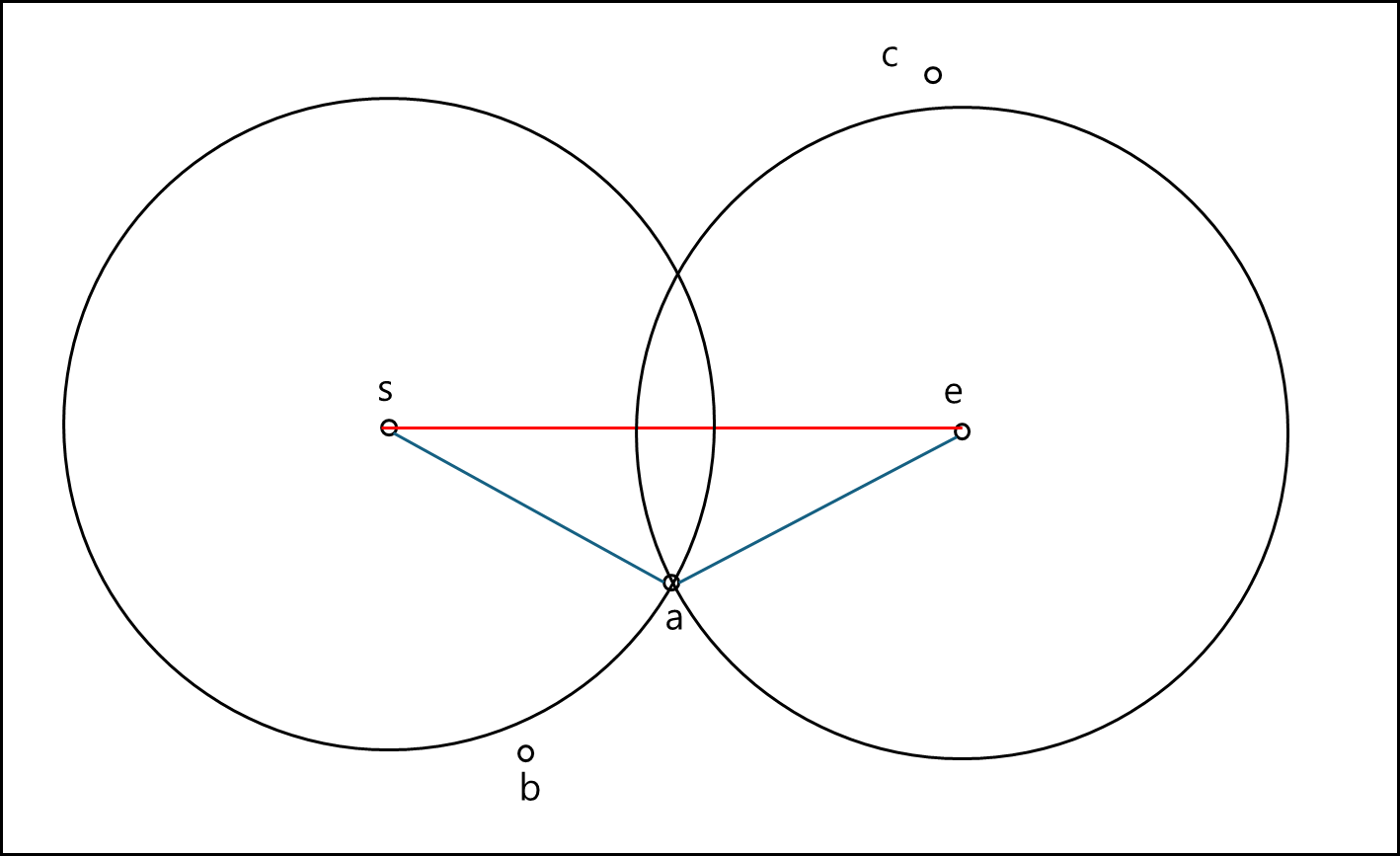
분할 리스트 SL과 새로운 데이터 포인트 p가 주어졌을 때, p가 NN인 시점을 찾기 위해 SL의 점이 하나 이상은 바뀌어야한다는 뜻이다. 간단히 보여주자면 아래의 그림과 같은 것이다.
위 그림의 경우 query line s에서 e까지있고 a,b,c가 있을 때 a가 가장 가까운 점이므로 위와 같이 a가 s부터 e까지 커버하고 s와 e는 분할점이 없다. 여기서 점 p가 아래와 같이 추가된다고 해보자.
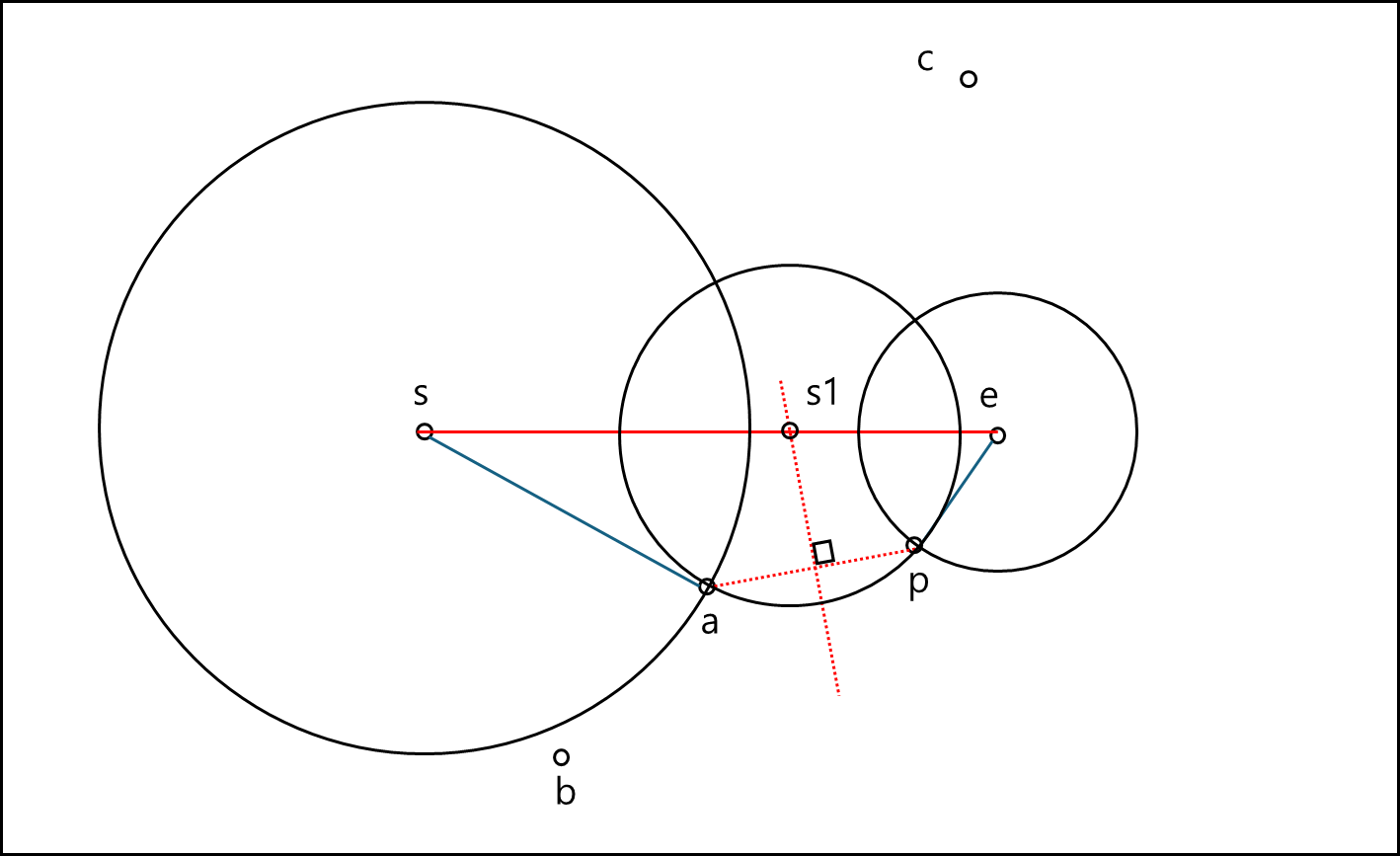
이렇게 되면 c가 커버하는 범위가 늘어나기 때문에 s1이 추가되어야한다. 이렇게 Data point가 추가되면 범위를 표현하기 위해 query line을 분할하는 점이 1개 이상 늘어나거나 위치가 변화해야한다.
2) Lemma 2 (Covering Continuity)
포인트 p가 커버하는 분할 지점들은 연속적이다. 즉, p가 분할 지점 s를 커버하지만 s₋₁이나 s₊₁을 커버하지 않는다면, p는 그 이후의 분할 지점들도 커버할 수 없다.
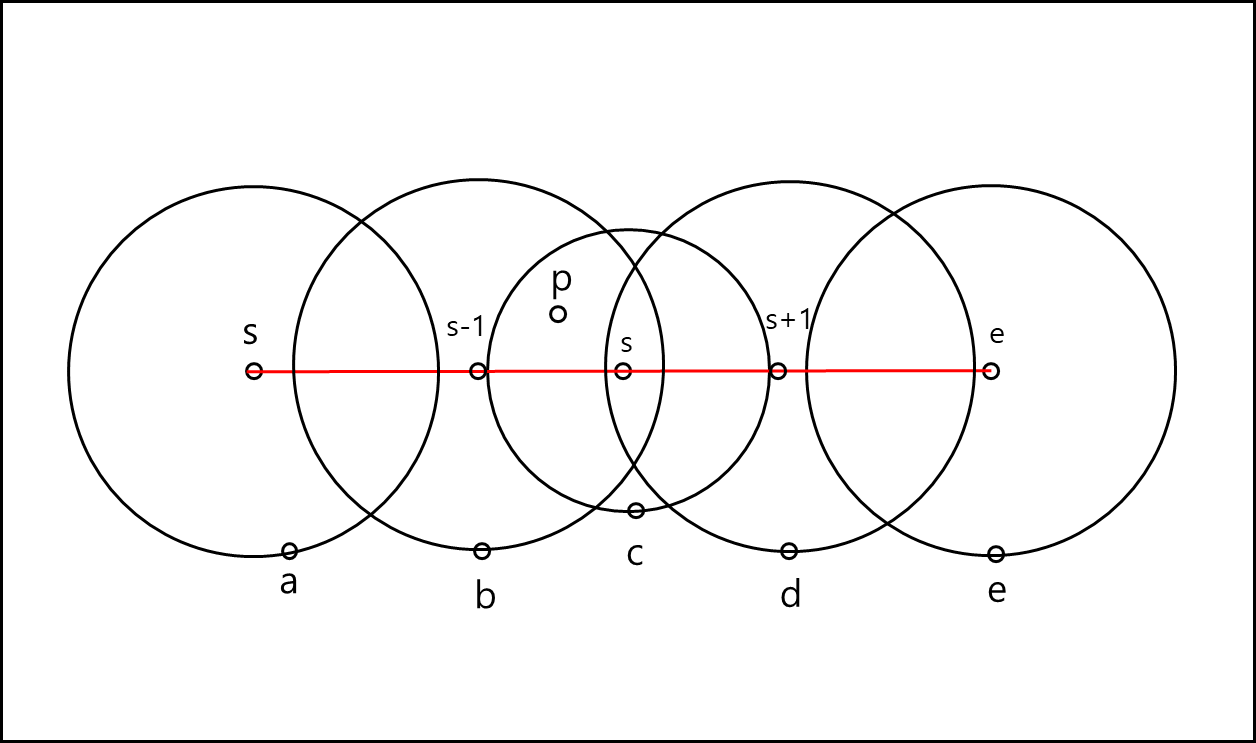
여기서 말하는 커버한다는 것은 점 p가 다른 분할 기준 점으로 그은 원안에 포함된다는 뜻이다. 아래의 그림을 보자.
어떤점 p가 있다. 이 점은 s-1과 s에 대해서 b와 c보다 가깝지만 d만큼 가깝지 못해서 s+1에는 영향을 주지 못한다. 이 말인 즉슨 s+2, s+3… 쭉 그 뒤 점과 최근접 점과의 거리로 그은 원에 포함되지 않는다.
3. Algorithm with R-trees Overview
1) Heuristic 한 방법의 가지치기
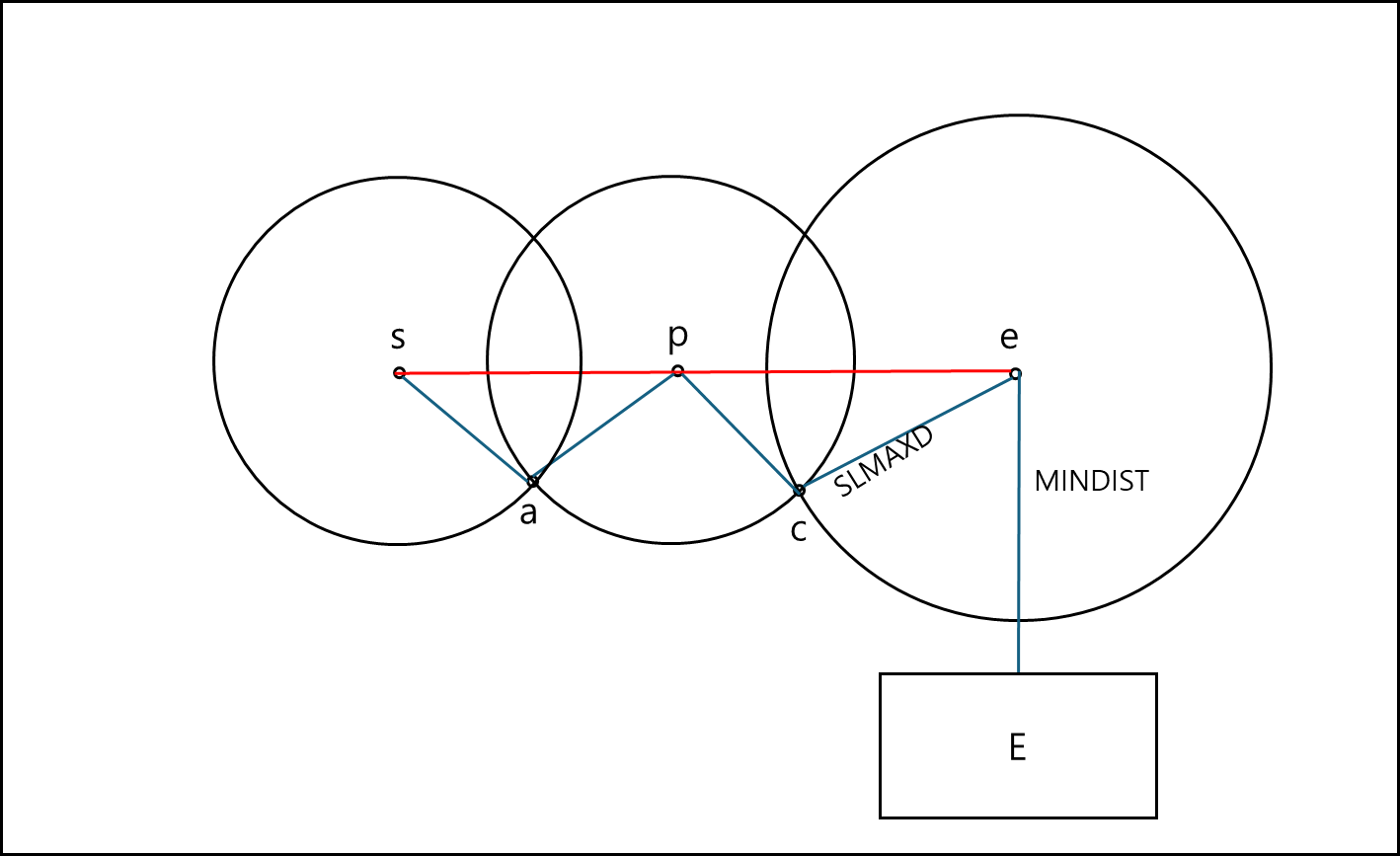
Heuristic 1
시작 점인 s와 도착점 e에 대해 그은 쿼리 선분 q에 대해서 중간 엔트리 E의 서브트리가 유효한 포인트를 포함할 수 있으려면 mindist(E,q) < SLMAXD를 만족해야 한다. 여기서 SLMAXD는 분할 지점과 그 최근접 이웃 간의 최대 거리를 말한다.
간단하게 그림으로 보여주면 아래와 같다.
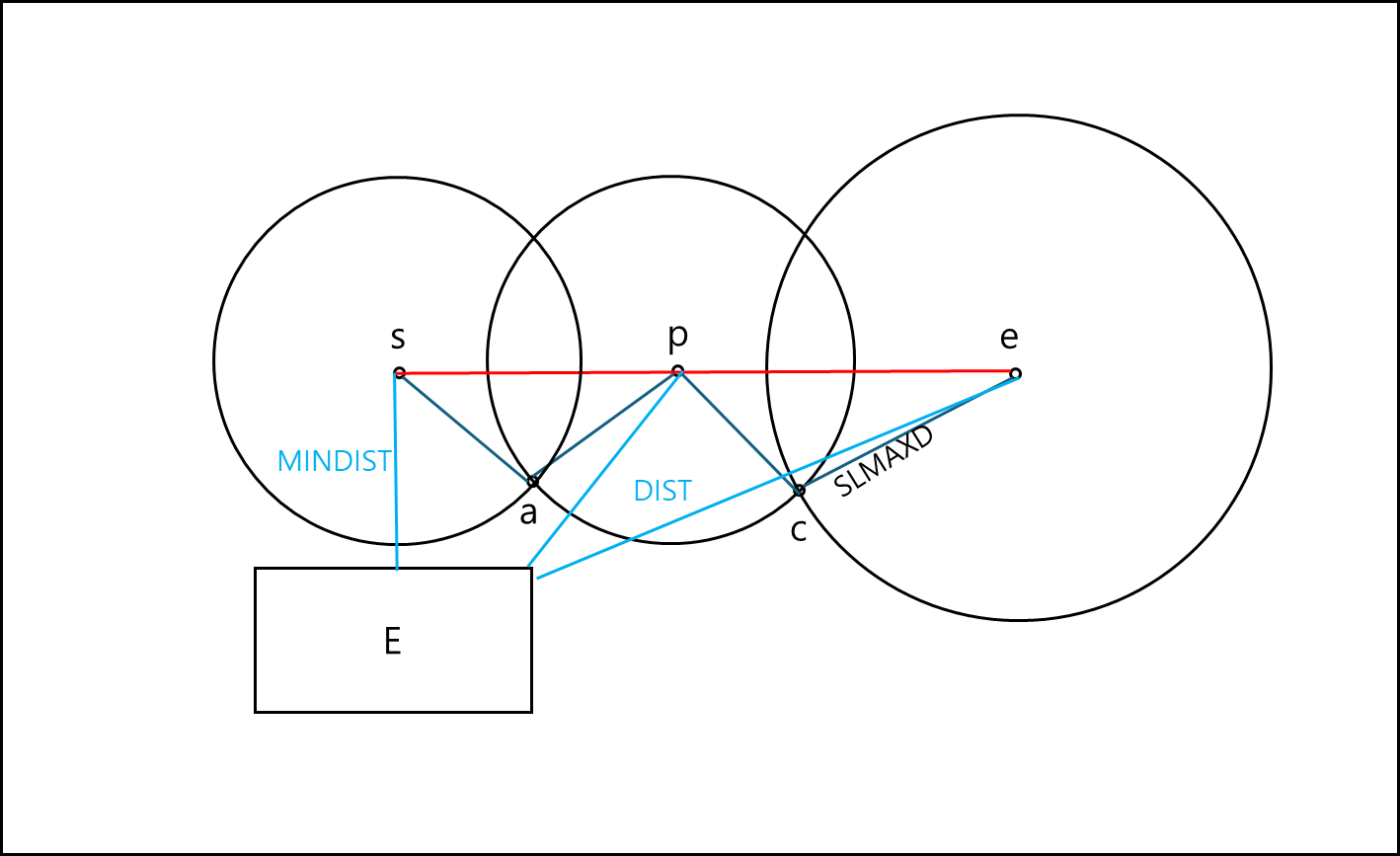
Heuristic 2
중간 엔트리 E의 서브트리를 탐색해야 하는 조건은, 분할 리스트에 dist(sᵢ, sᵢ.NN) > mindist(sᵢ, E)를 만족하는 분할 지점 sᵢ가 존재할 때이다.
기본적으로 아래와 같은 상황이다.
SLMAXD보다는 MINDIST가 짧지만 사실 어떤 가까운 점까지 그은 원 안에 포함되지 않는 것을 볼 수 있다.
이 경우 각 분할점까지의 거리를 잼으로써 실질적으로 원에 포함되는지 확인하는 것이다. 이 휴리스틱은 Heuristic 1을 통과한 경우에만 적용된다.
Heuristic 3
Heuristic 1과 2를 만족하는 엔트리들은 쿼리 선분 q까지의 최소 거리가 증가하는 순서로 접근한다.
요컨대 원에 가까운 MBR부터 search하면 이후 먼 MBR은 가지치기가 될 가능성이 높기 때문에 가까운 것 먼저하는 것이다.
2) 알고리즘
리프 엔트리(데이터 포인트) p를 만나면: 1) p가 커버하는 분할 지점들의 집합 S를 검색한다. 2) S가 비어있지 않으면 Split List를 업데이트한다. 이진 탐색을 사용하여 모든 분할 지점과 비교하는 것을 피하고 효율성을 높인다
업데이트 과정에서는 이전 최근접 이웃과 새로운 포인트 사이의 수직 이등분선과 쿼리 선분의 교점에 새로운 분할 지점을 추가하고, 기존 분할 지점들을 제거한다.
알고리즘은 기본적으로 R-tree에서 깊이 우선 탐색을 수행하며, branch-and-bound 기법으로 탐색 공간을 줄인다
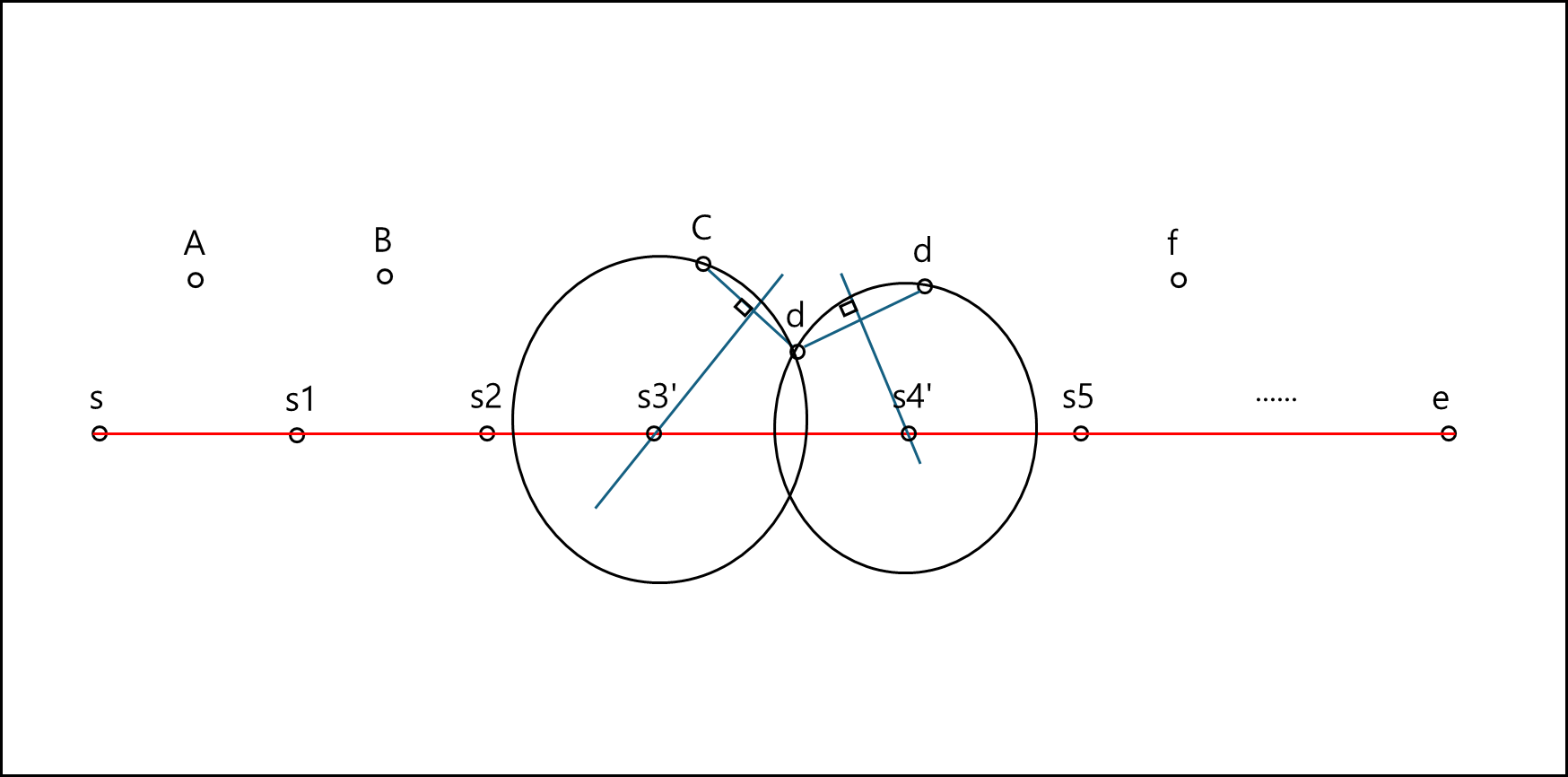
3) CNN 탐색 예시
그냥 알고리즘만 저렇게 설명해두면 이해하기 어려우니 예시를 들어 설명하겠다.
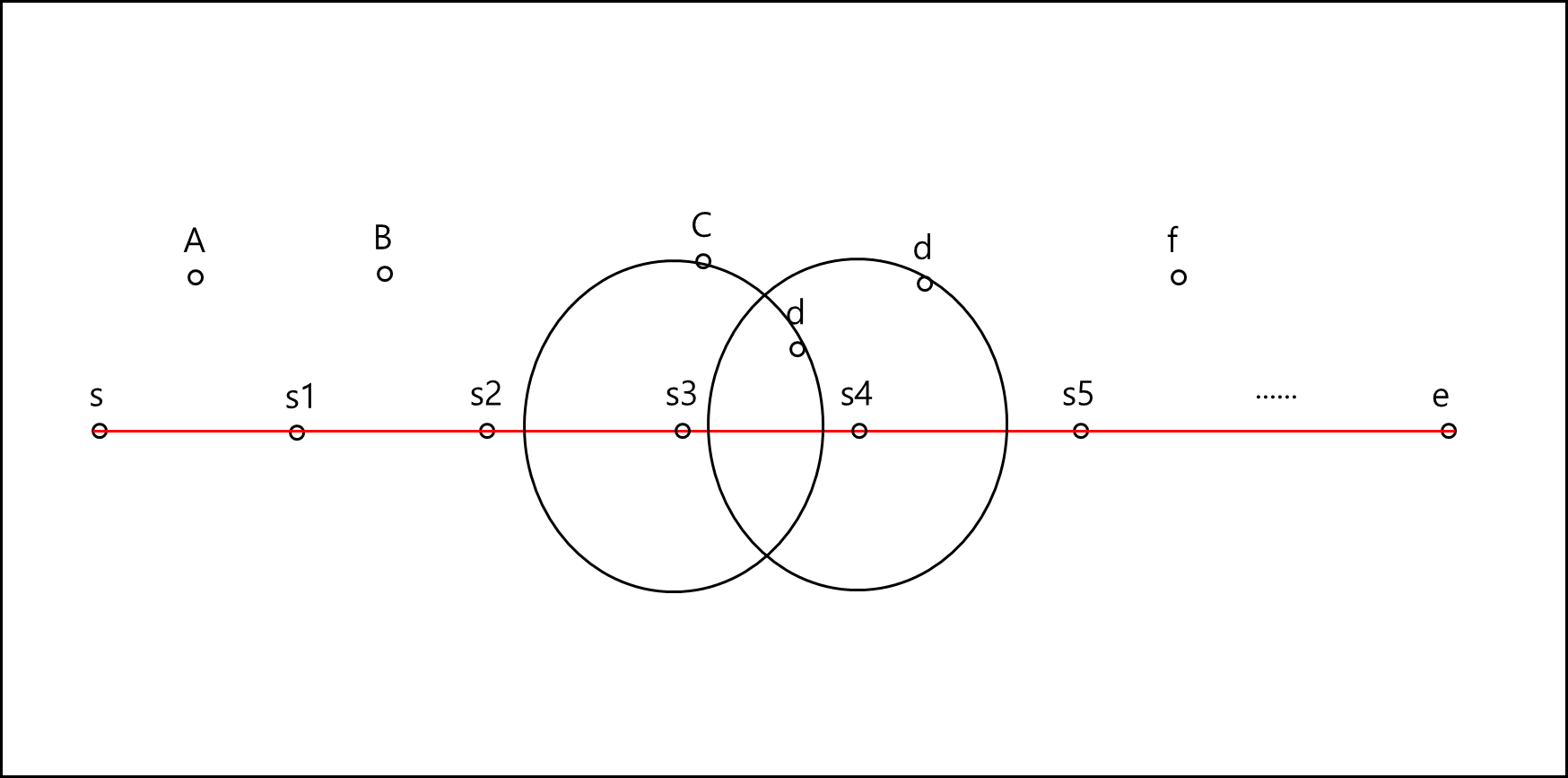
아래의 그림을 보자.
R-tree에서 DFS로 점 하나씩 찾아가면서 분할 점을 찾는 다. 이미 사전에 몇 개의 분할 점을 찾아서 S부터 S1~ E까지 있다고 해보자.
S3와 S4를 만드는 c와 d가 있었는데, p라는 점을 하나 더 찾게 되었다.
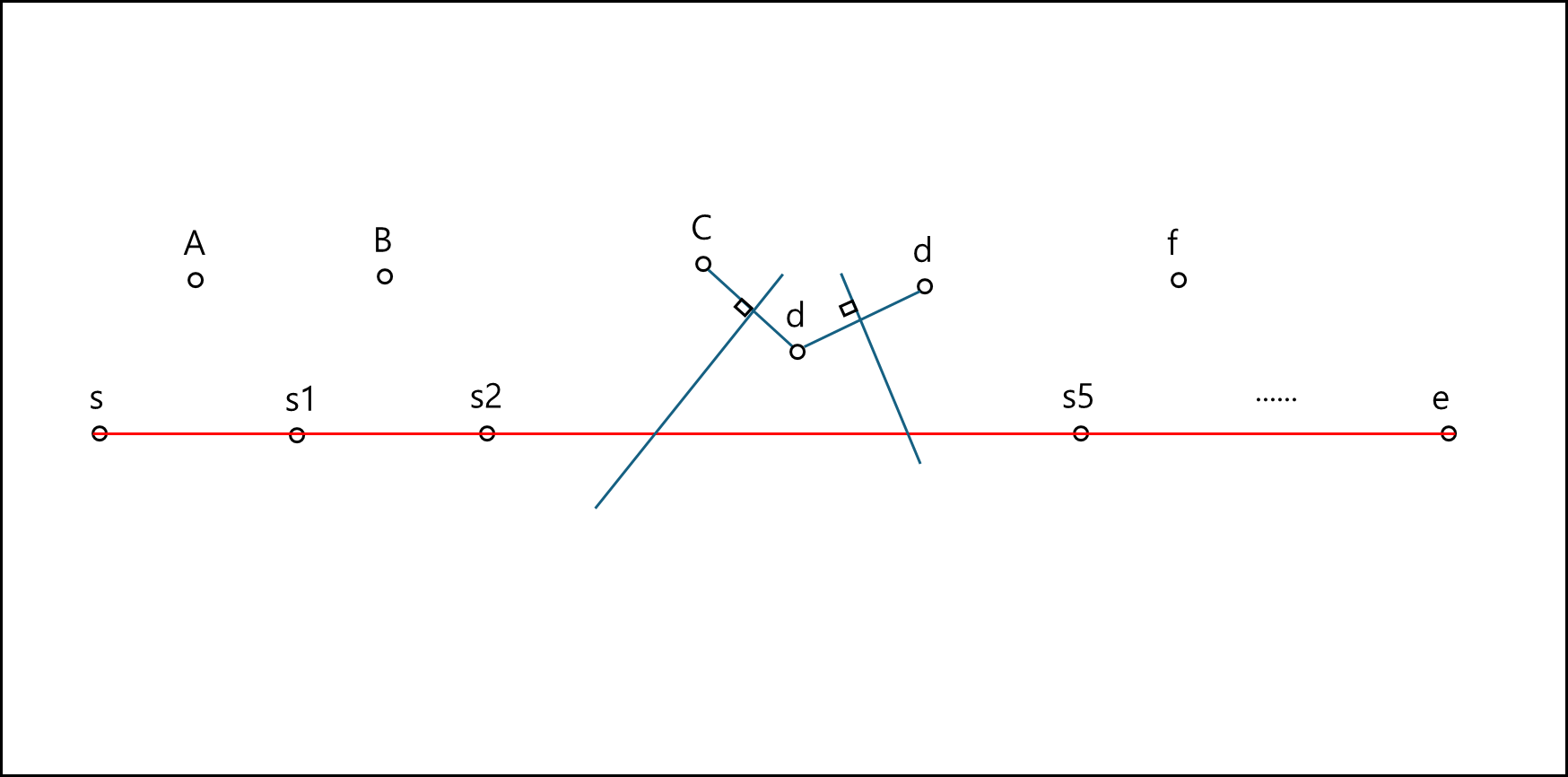
이렇게 되면 s3와 s4를 지워버리고 아래와 같이 c-p , d-p 선분을 직각 이등분하는 직선을 긋는다.
이후 이 직선을 확장했을 때 경로상에 닿는 점을 새로운 s3와 s4로 지정한다.
참고자료
- Shashi Shekhar and Sanjay Chawla, Spatial Databases: A Tour, Prentice Hall, 2003
- P. RIigaux, M. Scholl, and A. Voisard, SPATIAL DATABASES With Application to GIS, Morgan Kaufmann Publishers, 2002