Post

공간 데이터 베이스 - M-Tree

Posted Updated
By Blake Woo 15 min read

M-tree

1. 개요

앞서 포스팅했던 Space-driven 방식이나 Data-driven 방식의 경우에는 한 가지 공통점이 있다.
바로 차원의 저주에 취약하다는 점이다.
차원의 저주라는 것은 차원이 늘어나면 늘어날 수록 어떤 방식이든 간에 데이터가 넓게 퍼져버리는 것이다.
이렇게 데이터가 넓게 퍼져버리면 결론적으로 전체 Scan하는 것과 다를바 없이 성능이 떨어져버리게 된다.
이를 방지하고자 거리에 대해서 Mapping하는 방식이 있는데 이를 M-tree라고 한다.

2. 구조

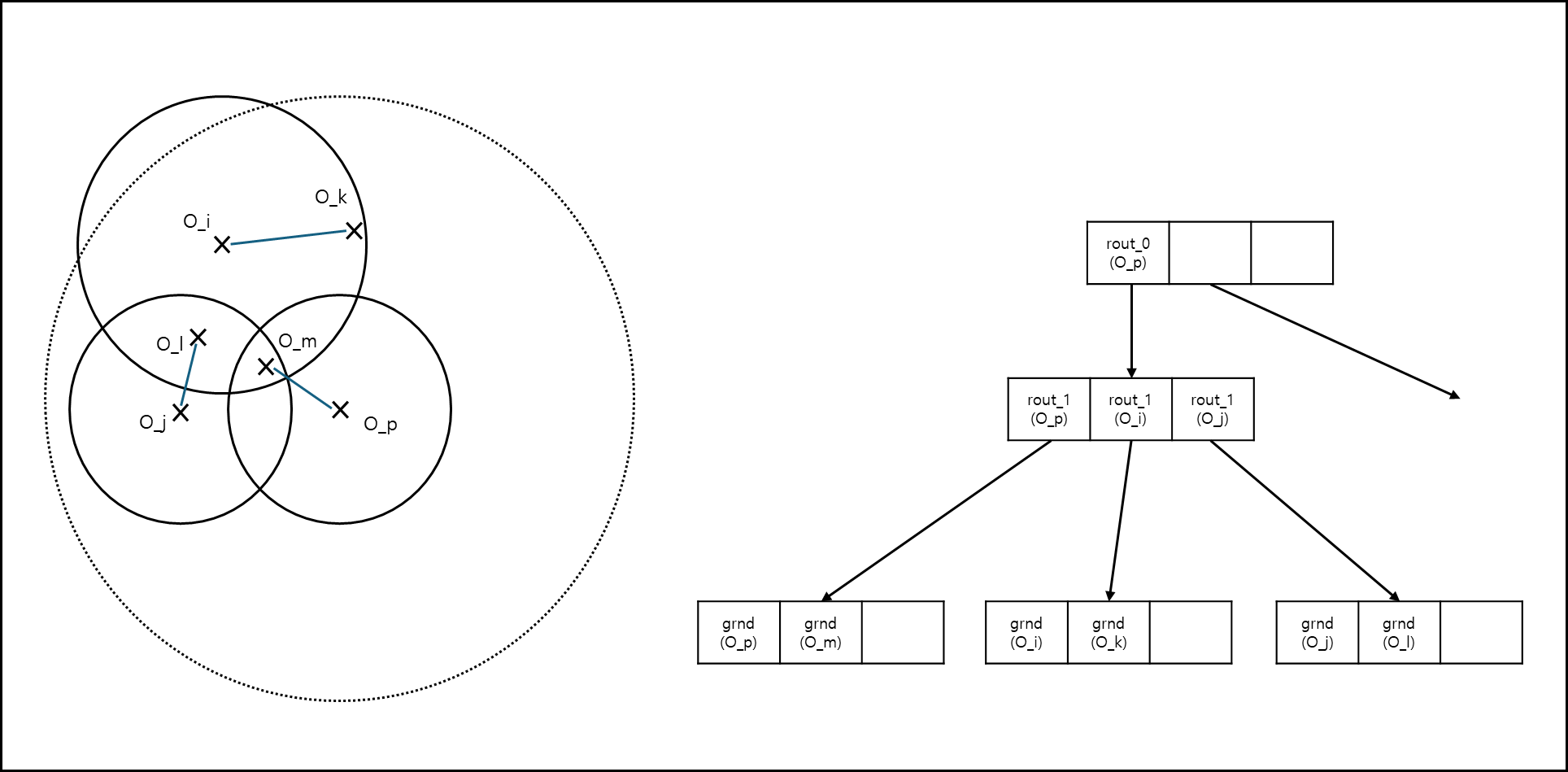
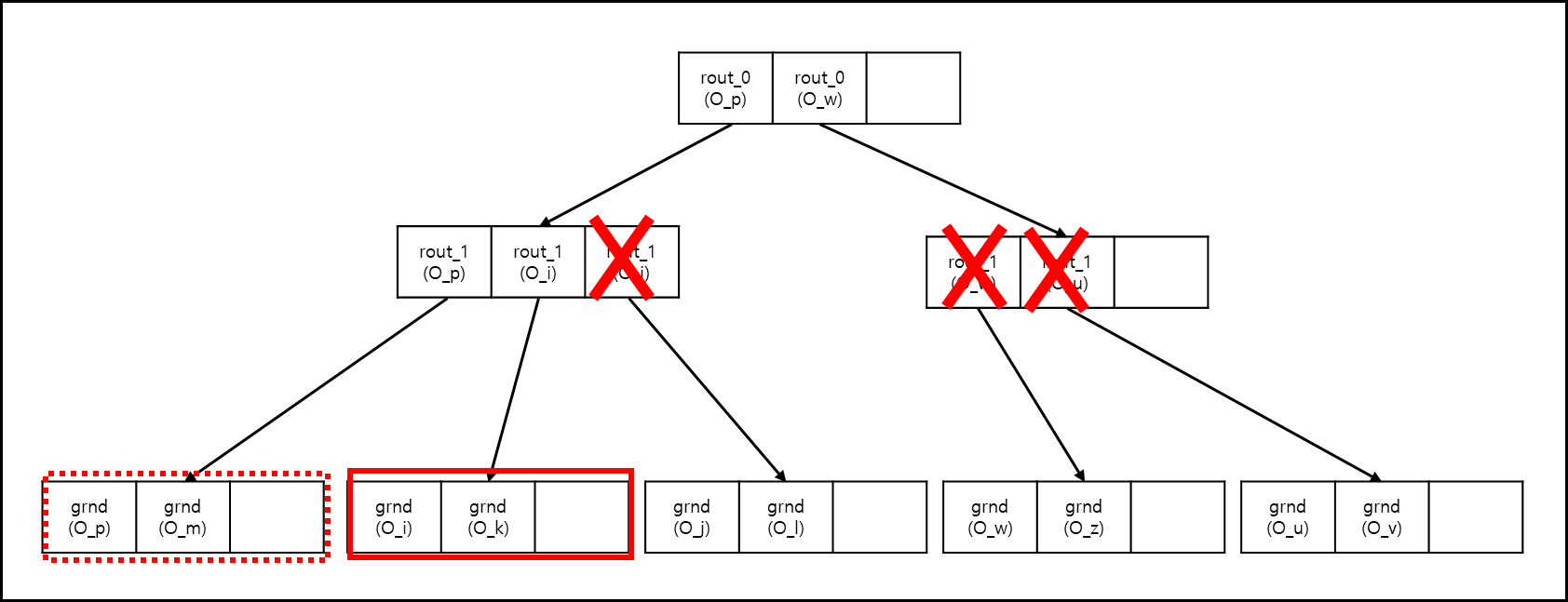
M-tree의 구조는 아래와 같다.

img.png

말 그대로 Tree의 형태를 취하고 있으며 상위 노드의 엔트리들은 원의 형태로 하위 노드를 포함하고 있는 형태를 취하고 있다.

위에서 rout과 grnd라고 표시한 두 종류의 엔트리가 있다. rout은 routing object를 말하며, grnd는 ground object를 말한다. 이는 각각 Internal node와 Leaf node가 object들을 담고 있다. 이에 대한 설명은 아래와 같다.

1) Leaf node

실제 객체의 정보를 담고 있는 node이다.

  • Object : ground object의 정보, 즉 실제 객체의 정보이다.
  • Distance of parent pivot : object의 값과 상위 Node의 Pivot과의 거리를 담고 있다.

2) Internal node

실제 객체 정보를 담고 있는 node를 찾아가기 위한 node로 각각의 엔트리는 routing을 위한 객체이다.
Node의 각각 엔트리(routing object)는 아래와 같은 정보를 담고 있다.

  • Pivot : p로 표현하며, 원의 중심부이다.
  • 반지름 : 서브트리를 담기위한 원의 반지름이며 $r^{c}$ 로 표현한다.
  • 상위 노드의 Pivot과 거리 : 상위 노드를 이루는 원과의 중심부와의 거리를 말하며 해당 node가 ROOT일 경우에는 이 값이 없다.
  • 서브트리 포인터 : 서브트리로 연결된 포인터이다.

3. Insertion

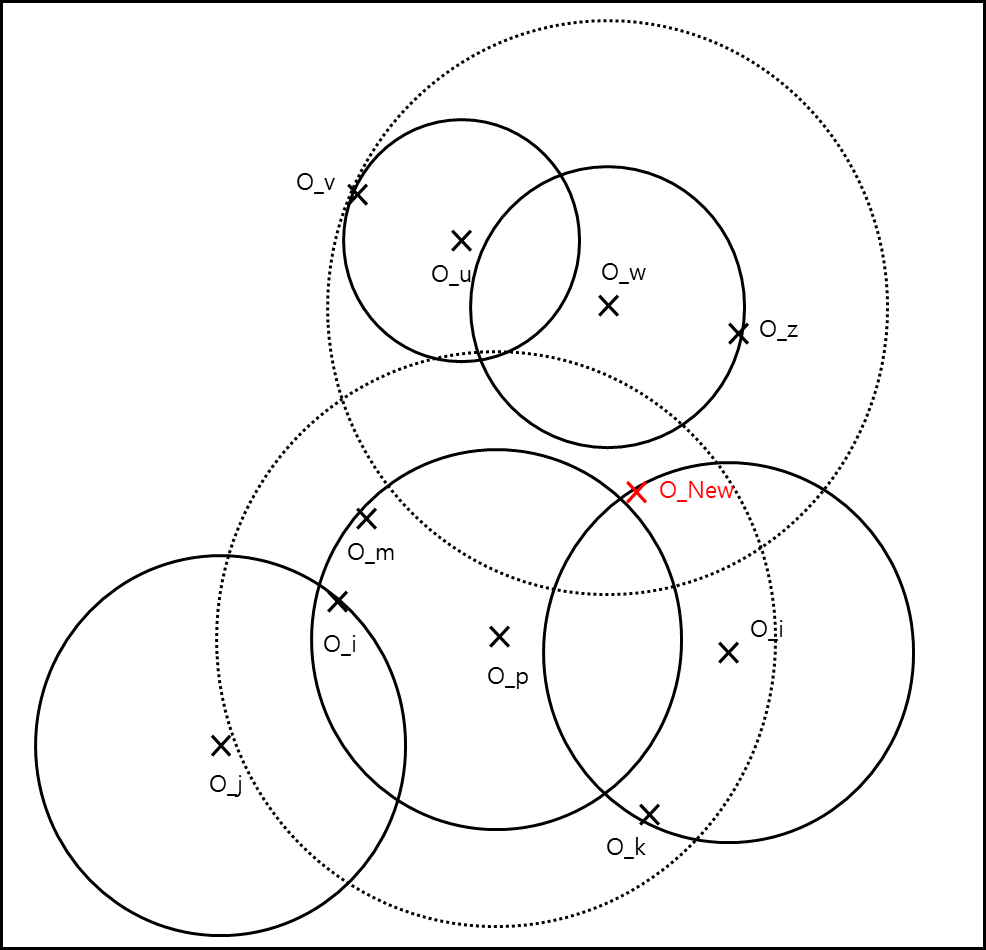
아래와 같은 생황에서 O_New 객체가 새로 추가되었다고 해보겠다.

img_1.png

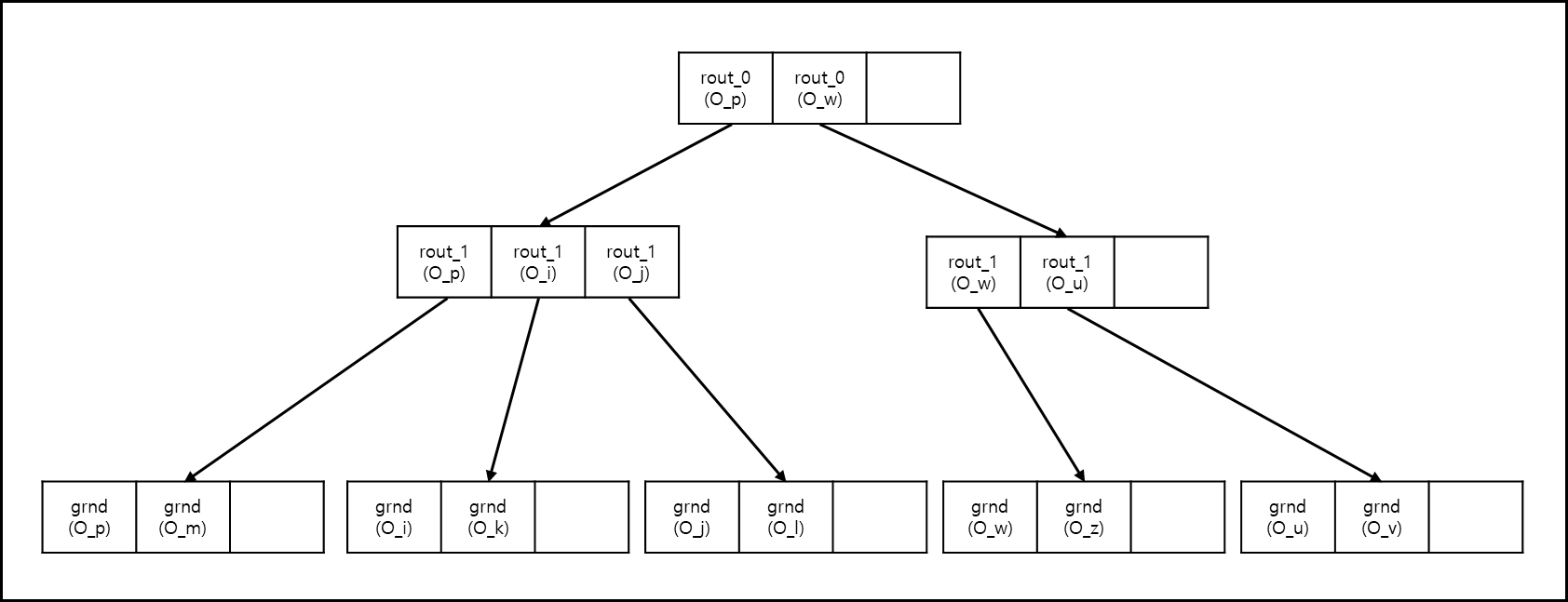
위 그림을 트리로 나타내면 아래와 같다.

img_2.png

1) Single way insertion

말 그대로 한번에 한 개의 Entry만 고려하는 방법이다.

  1. 루트 노드에 있는 O_p와 O_w와 거리를 O_New를 계산한다. O_w와의 거리가 더 짧기 때문에 해당 객체의 하위 node를 탐색한다.
  2. 하위 노드의 O_w와 O_u와의 거리를 검사한다. O_w와의 거리가 더 짧기 때문에 해당 객체의 하위 node를 본다.
  3. node를 보니 Leaf node이다. node에 남은 공간이 있다면 바로 추가하고, 없다면 Split(아래에서 서술)해서 넣는다.
  4. Entry 추가 후 routing object의 범위가 부족하다면 반지름을 늘려서 Entry를 포함하도록 한다.

img_3.png

2) Multi way insertion

한번에 다 수개의 Entry를 고려하는 방법이다.
Single way는 Pivot과의 거리만 고려했다면 Multi way는 routing object의 반지름까지 고려하여 추가할 값이 해당 범위 안에 들어오는지 고려한다.

  1. 루트 노드에 있는 rout0(O_p)와 rout0(O_w)의 원에 O_New가 포함되는지 확인한다. 둘다 포함되므로 먼저 rout0(O_p)의 하위 노드부터 탐색한다.
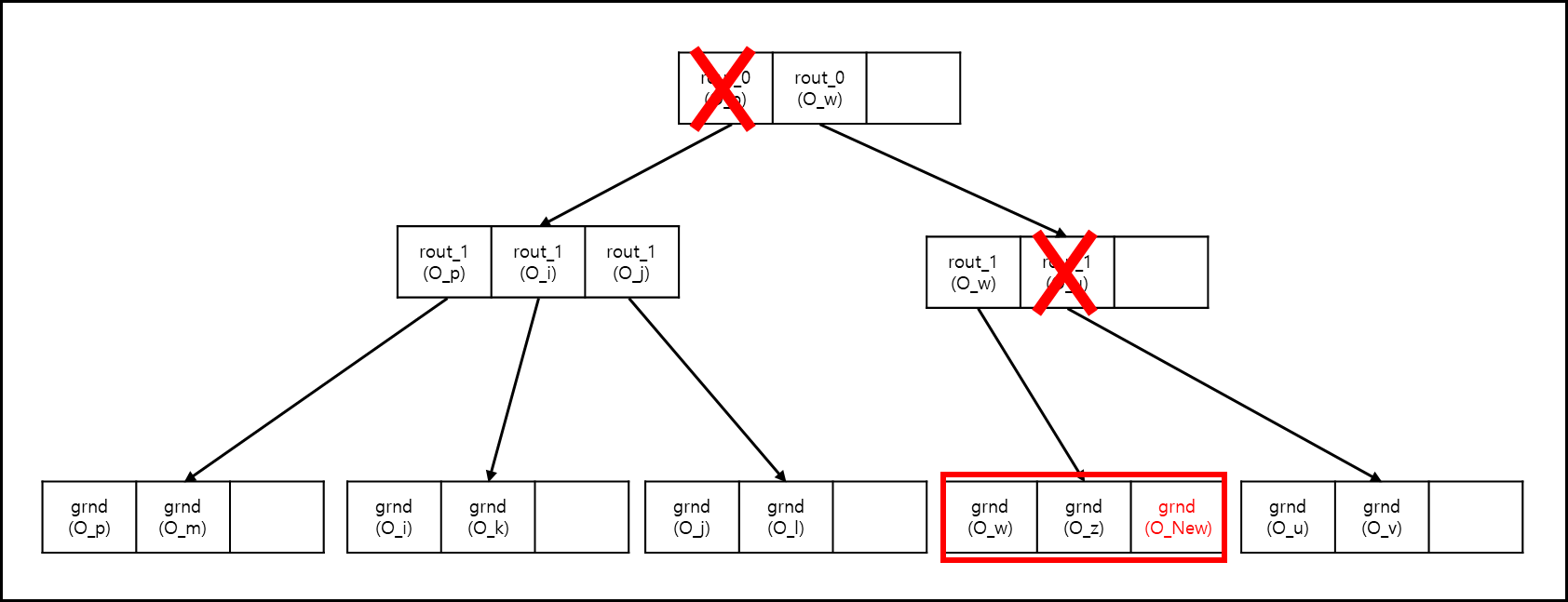
  2. rout0(O_p)의 하위 노드를 확인하여 각 엔트리의 원에 포함되는지 확인한다. rout1(O_p)와 rout1(O_i)는 포함되지만 rout1(O_j)는 포함되지 않는다. 먼저 rout1(O_p)의 하위 노드를 탐색한다.
  3. rout1(O_p)의 하위노드는 Leaf Node이므로 삽입 가능 후보군에 넣어두고 다시 부모 노드로 돌아간다.
  4. 그 다음은 rout1(O_i)의 하위 노드인데, 이 역시 Laef Node이다. 삽입 가능 후보군에 있던 Node의 Pivot과 거리를 재본다.
  5. rout1(O_i)의 Pivot이 rout1(O_p)보다 거리가 더 짧으므로 rout1(O_p)의 하위 노드는 가지치기 해버리고 rout1(O_i)만 후보로 남겨둔다.
  6. 다시 위로 올라가서 루트 노드로 가서 rout0(O_w)의 하위 노드를 검사한다. 하지만 하위 노드의 객체들의 원은 O_New를 포함하지 않으므로 가지치기된다.
  7. 후보군인 rout1(O_i)가 선택되어 해당 노드의 용량이 가득차지 않았다면 삽입하고, 가득찼다면 split(아래에서 서술)후 포함한다.

img_4.png

4. Split

용량이 꽉찬 node에 어떤 entry를 삽입하고자 할 때하는 연산이다.
기본적으로 꽉찬 node의 엔트리 중에 두 개를 Pivot으로 선택 후 남은 Entry를 각 Pivot에 분배하여 나누는 식인데 어떻게 Pivot을 선택할 것인지와 나눈 Pivot을 대상으로 어떻게 분배할 것인지 분배 후 어떻게 트리에 삽입할 것인지가 달라진다.

1) Pivot selection

크게 네 가지로 나뉜다.

  • Random : 말 그대로 무작위로 두개 뽑는다.
  • m_RAD : Pivot 1,2를 선택하되 분배 후 반지름이 최소가 되는 값으로 선정한다.
  • mM_RAD : Pivot 1,2를 pair로 선택하되 각각의 반지름을 구했을 때 큰 것들 중에 작은 것을 선택한다.
  • M_LB_DIST : Pivot 1은 부모 Pivot을 설정 후 거리가 가장 먼 객체를 Pivot 2로 선정한다.

사실상 두 개의 Pivot을 선택하는 방법은 두 가지인셈이다.

  • Confirmed : 한 개는 부모 Pivot을 쓰고 다른 한 개를 선택
  • Unconfirmed : 두 개 다 선택

2) Split Policy

두 개의 Pivot을 선택했다면 남은 엔트리를 분배해야하는데 분배 방법은 크게 두 가지 이다.

a. Unbalanced

Pivot 두 개의 거리를 구해서 절반까지의 범위에 든 것들을 각각의 Pivot에 Mapping한다.

b. Balanced

각 각의 Pivot 가장 가까운 엔트리를 하나씩 선택하여 포함한다. 각각 Pivot에 속한 엔트리 개수는 비등해지나 기본적으로 Unbalanced한 방법보다 성능이 안나온다.

Range Search는 어떤 점 O_q가 있고 그에 따른 반지름 r_q가 주어졌을 때 해당 원 안에 들어오는 점들을 찾는 것이다.
기본적으로 M-tree의 Leaf Node의 모든 Entry는 상위 노드의 Entry들의 원에 포함되는 형태이다. 이를 이용하면 쿼리와 부모 피벗과의 거리를 이용해 빠르게 가지치기를 할 수 있다. 각 엔트리들은 부모 피벗과의 거리가 모두 저장되어있기 때문이다.

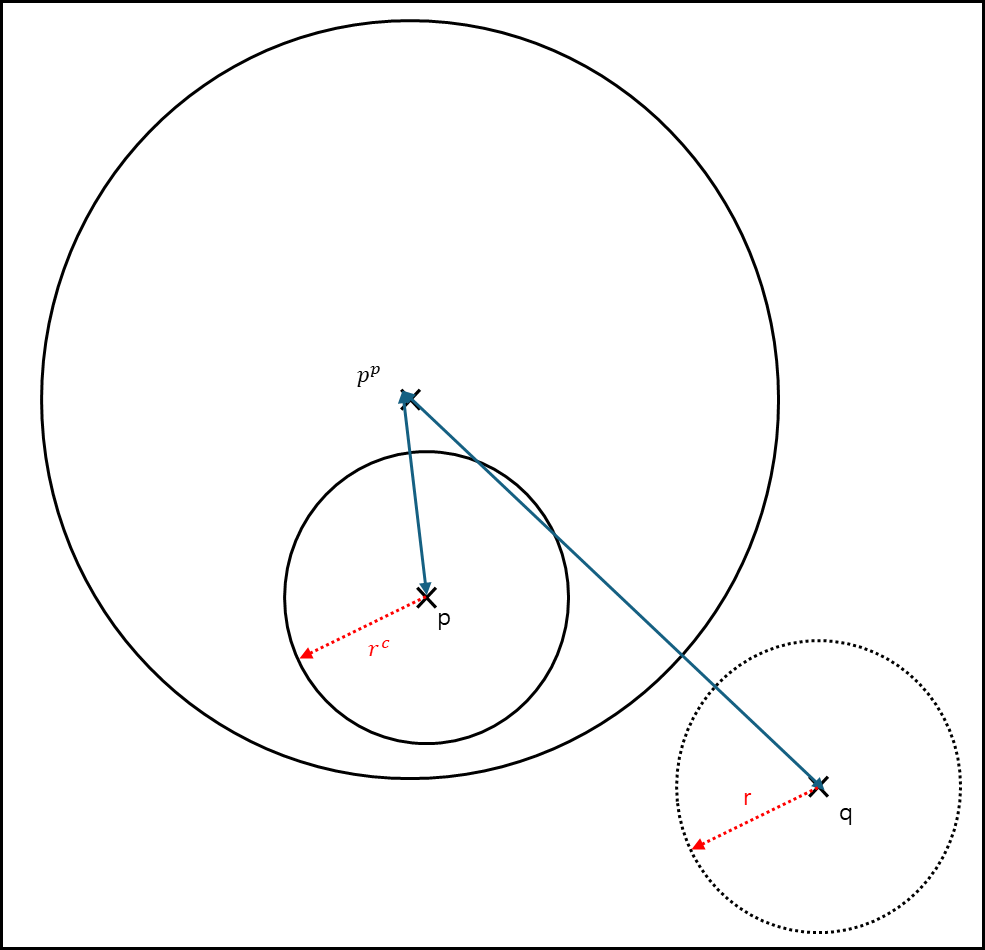
a. 가지치기

쿼리 q와 쿼리의 반지름 r에 대해서 부모 피벗 $p^{p}$ 와 검사하고자하는 점 p와 그의 반지름 $r^{c}$가 있다고 해보자.
가지치기 할 수 있는 경우는 아래와 같다.

ⓐ 부모원($p^{P}$ 와 그의 반지름) 바깥에 있을 경우

img.png

ⓑ 부모원 안에 있으나 q의 범위안에 포함되지 않는 경우

img_1.png

위 두 가지의 경우 아래의 수식으로 가지치기 할 수 있다.

\[\left| d(q,p^{p})-d(p,p^{p}) \right| - r^{c} > r\]

위 수식은 삼각부등식을 변경한 것을 응용하여 세운 식이다.
삼각부등식은 한 변의 크기는 두 변을 합한 것보다 클 수 없다를 수식으로 나타낸 것이다.
점 a,b,c가 있고 d는 두 점 사이의 거리를 구하는 함수일때, 세 점으로 삼각형을 만든다고 하면 아래의 수식을 만족한다.

\[d(a,b) \le d(b,c) + d(a,c)\]

이는 점을 바꿔도 마찬가지이다. 이를 이용하면 다음과 같은 식을 산출할 수 있다.

\[d(a,b) - d(b,c) \le d(a,c)\]

사실 상 두 거리를 빼면 다른 한 거리보다 작거나 같아야한다. 만약 두 원이 접해있다면 두 점 사이의 거리는 각각 원의 반지름을 합친 값과 같다.
따라서 첫번째 식으로 가지치기가 가능한 것이다.

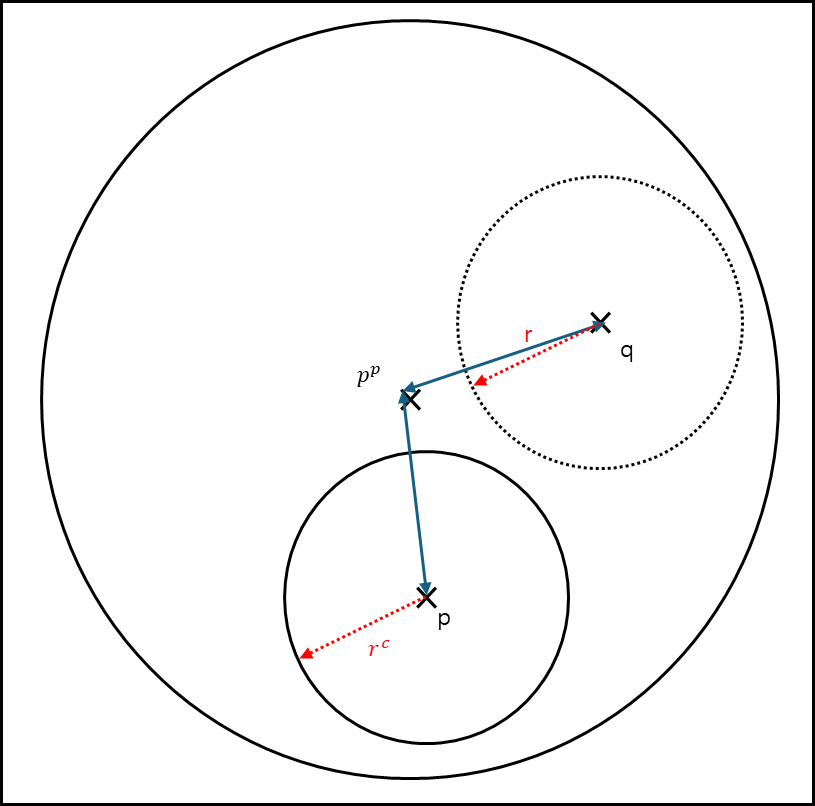
ⓒ p와 q를 거리를 구한 값에 p의 반지름을 뺐을 때 q의 반지름보다 작을 경우

위의 가지치기를 하고도 남은 것들은 q의 반지름에 드는지 직접 검사해야하며 반지름보다 멀 경우에는 q와 r로 이루어진 원 내에 포함되어있지 않으므로 당연히 가지치기를 해야한다.

b. 리프노드 검사

가지치기가 완료된 리프노드들에 Entry를 하나씩 꺼내서 해당 범위 안에 포함되는지 다 확인해봐야한다.
리프노드 안에 Entry를 o라고 하고 리프노드의 바로 상위 노드의 Pivot을 $o^{p}$ 라고하면 아래의 식에 넣어서 확인한다.

\[\left| d(q,o^{p}) - d(o,o^{p} \right| > r\]

식을 만족하는 엔트리들을 반환하면 된다.

고정된 반지름 대신에 k번째 가까운 이웃을 반지름으로 사용하여 K-NN을 구하는 방식이다.
서브트리 엔트리에 대해서 하한 $d_{min}(E)$ 를 계산해서 우선 순위 큐에 넣고 하한이 가장 작은 것부터 확장 탐색하는 방식으로 처리한다. 순서는 아래와 같다.

  1. 우선순위큐 PQ를 만든다. PQ는 두 점 사이의 거리가 작은 엔트리일 수록 앞에 온다.
  2. 후보자 큐 MQ를 만든다. Max힙으로 이루어져있으며 거리가 클수록 앞에 온다. 가장 앞의 값은 R_cur가 되며 비어있을 경우 R_cur의 값은 무한이다.
  3. PQ에 루트 엔트리들을 넣는다.
  4. PQ가 빌 때까지 아래를 수행한다.
    • PQ에서 1개 엔트리를 pop한다. 임의로 E라고 칭하겠다.
    • MQ가 K개면 반복문 종료
    • E가 내부 노드라면 그 자식 엔트리들에 대해 각각 $d(min)$을 계산하여 PQ에 넣음
    • E가 리프 노드라면 각 엔트리인 o에 대해서 아래와 같은 가지치기를 한다.
      $ \left| d(q,o^{p}) - d(o,o^{p} \right| > R_cur $ 이면 실제 계산은 pass한다.
      위 식을 성립하지 않으면 실제 $d(q,o)$ 를 계산하여 MQ에 넣는다. K개가 넘는다면 가장 먼 것을 꺼내고 K개로 유지하고 MQ에서 가장 앞에 엔트리 거리를 R_cur 값으로 선정한다.
  5. PQ가 빌때까지 반복하거나 MQ가 K개면 중단되고 종료된다.

※ 추가 업데이트 및 검증 예정이다.

참고자료

  • Shashi Shekhar and Sanjay Chawla, Spatial Databases: A Tour, Prentice Hall, 2003
  • P. RIigaux, M. Scholl, and A. Voisard, SPATIAL DATABASES With Application to GIS, Morgan Kaufmann Publishers, 2002
Database
Computer science Database Spacial Database M-Tree
This post is licensed under CC BY 4.0 by the author.