공간 데이터 베이스 - 최근접 이웃 검색(R-tree)

R-tree에서 최근접 이웃 검색

1. 개요

Vector DB에서 말하는 그 최근접 이웃이 맞다. 하지만 ANN을 다루는 것과 달리 공간 데이터 베이스에서는 진짜로 제일 가까운 값을 반환해주어야한다. 이를 위한 방법에 대해서 이번 포스팅간에 알아보겠다.

2. Depth-first Search

쿼리를 Q라고 하자. 이 Q에서 가장 가까운 점 또는 객체를 찾기 위한 가장 심플한 방법이다. DFS라고 하지만 사실 R 트리를 하나씩 Search해서 알아보는 것과 같다. 각각의 Entry들과 Q를 비교하여 가장 가까운 것을 뽑아내는 것으로 사실상 전체 검색과 다를바 없다.

3. Branch and bound

95년도 sigmod에 나온 논문으로 여기서는 각 Node별로 우선순위큐가 있다. 그리고 우선 순위는 기본적으로 MINDIST에 의해 결정되며 가지치기를 위한 MINMAXDIST가 있다. 쿼리를 Q라고 하자.

1) MINDIST

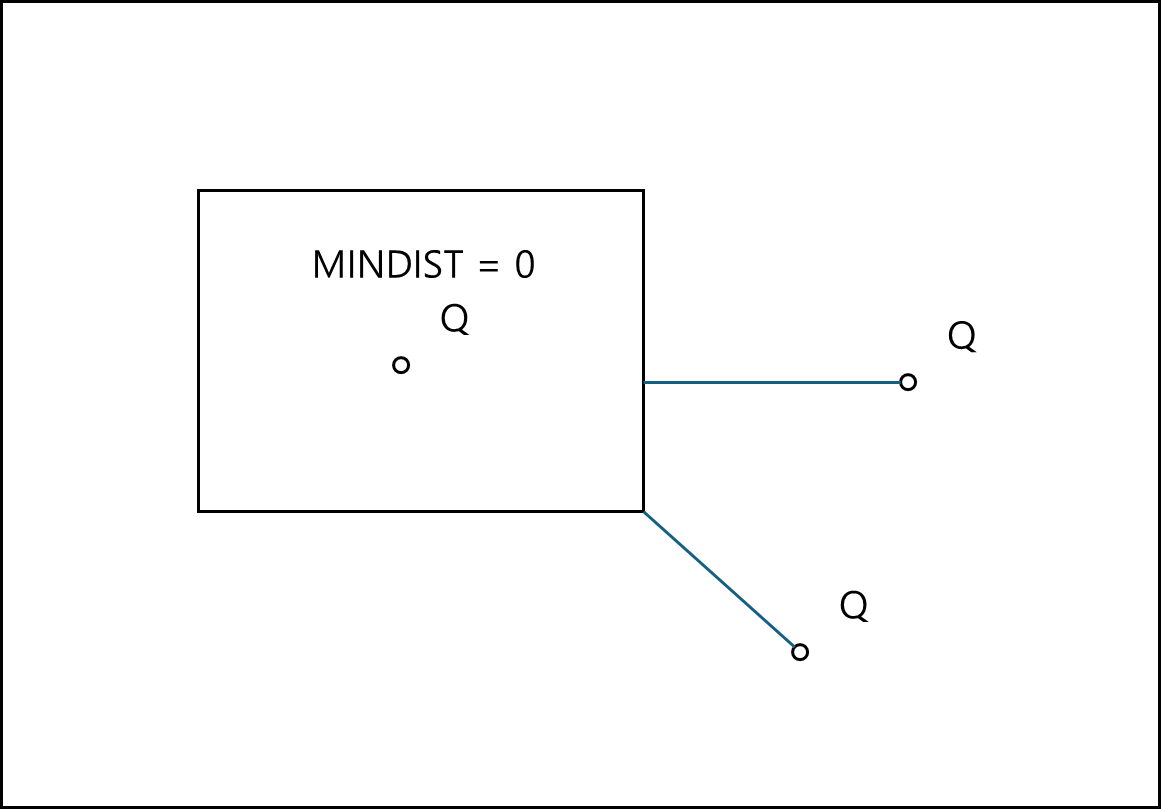
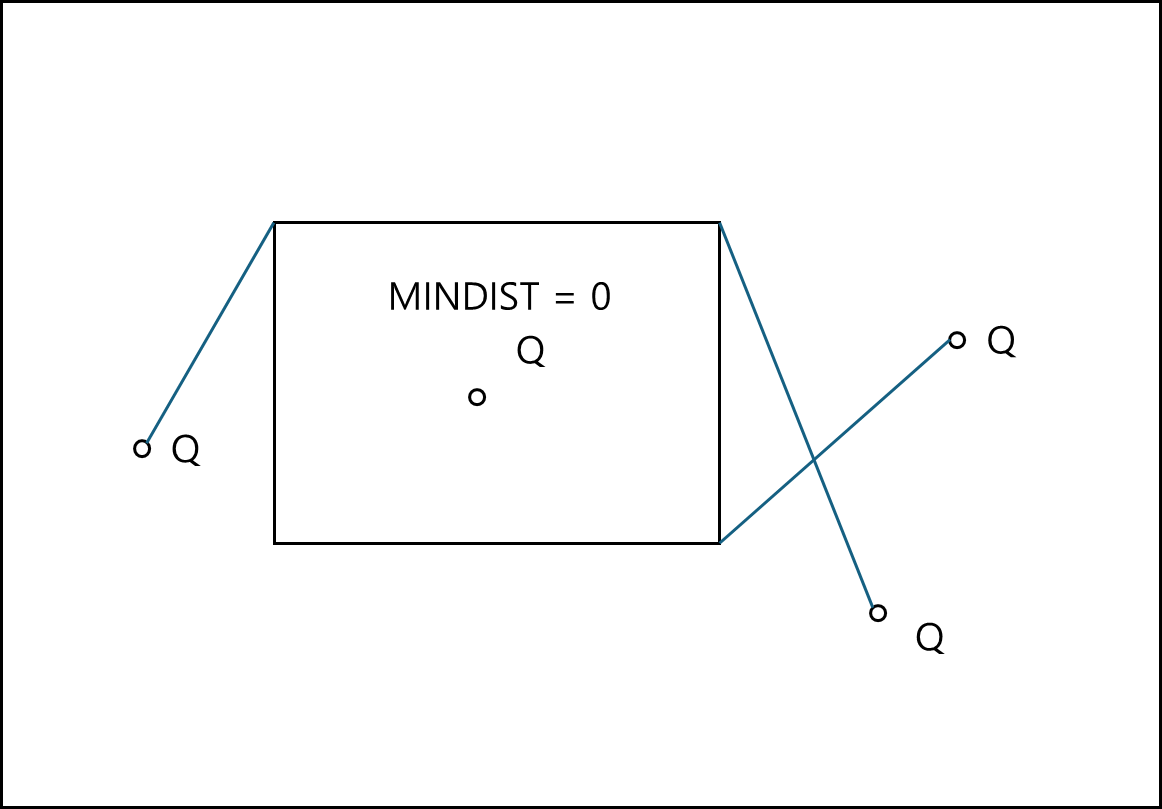
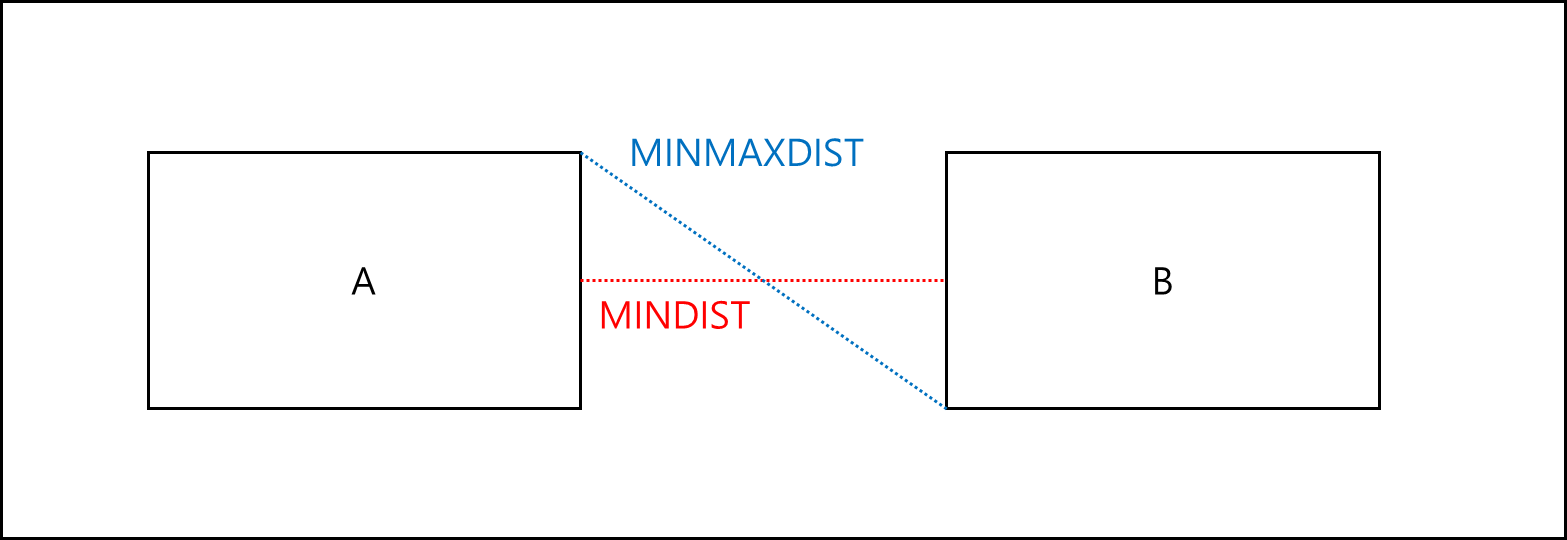
MINDIST는 Q에서 대상 MBB에서 가장 가까운 거리를 MINDIST라고 한다. Q와 대상 MBB에 가장 가까운 곳에 점을 찍고 Q와 선을 연결할때 변에 가깝다면 변에 직교하는 형태이거나, 혹은 꼭지점과 Q가 연결되는 형태이다. 모든 MBB에 대해서 MINDIST를 구했을 때 가장 작은 MINDIST보다는 긴 거리에 최근접 이웃이 있다.

2) MINMAXDIST

가장 가까운 변의 가장 먼 점까지의 거리를 말한다. 그래서 가장 가까운(MIN)변에서 먼(MAX)점과의 거리라고 MINMAXDIST이다.
이 거리가 설명하는 것은 어떤 최근접값은 모든 MBB의 MINMAXDIST중에 가장 작은 값보다 짧은 거리내에 최근접 이웃이 있다는 뜻이다.

3) Branch pruning

위와 같은 MINDIST와 MINMAXDIST를 통해 가지치기를 할 수 있다.

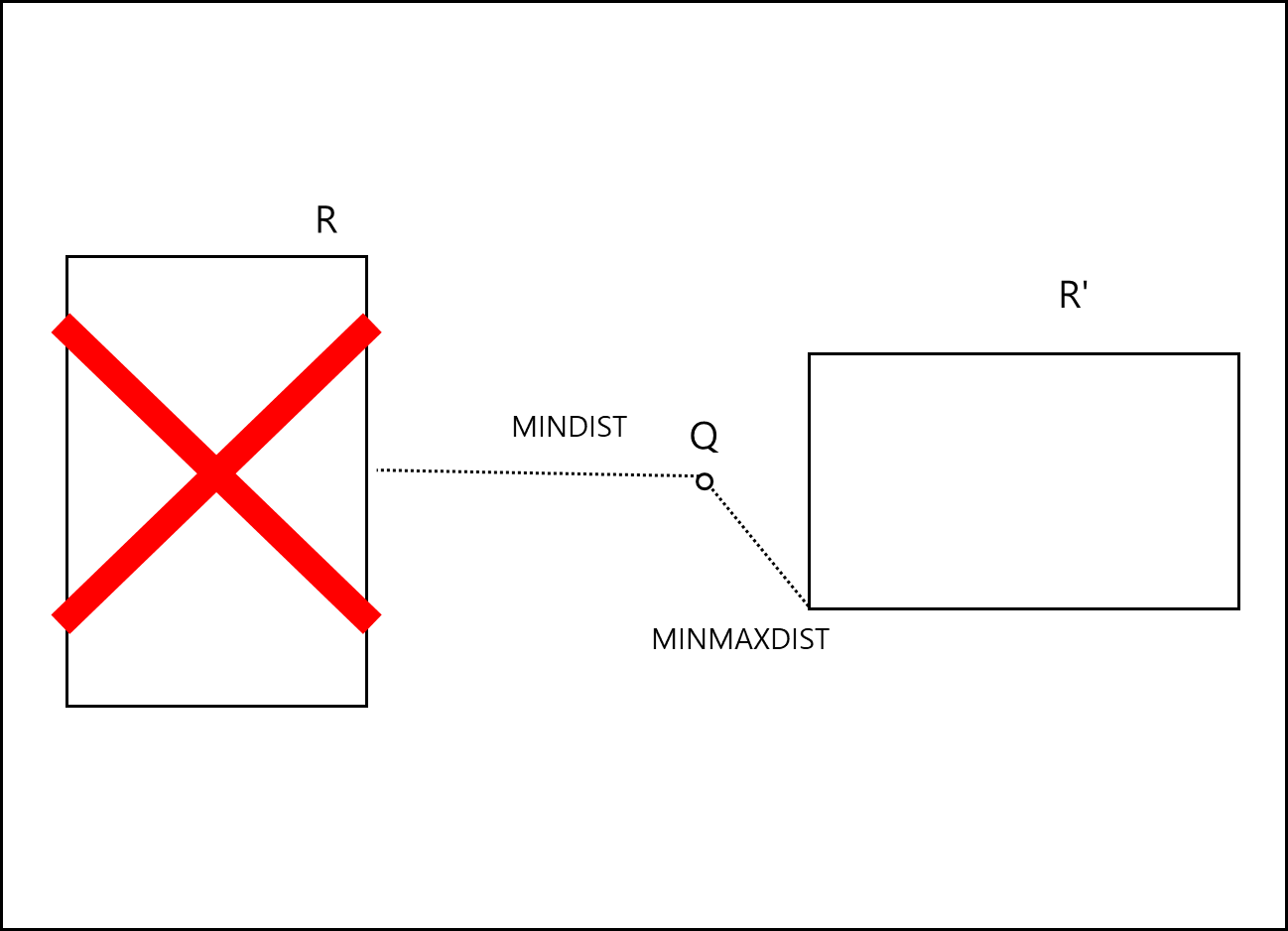
• 규칙 1. 상위 노드에서 하위 노드로 탐색시 : 어떤 MBB인 R에 대해서 MINDIST가 어떤 MBB인 R’의 MINMAXDIST보다 크다면 R에 대해서 탐색하지 않아도 된다.

  

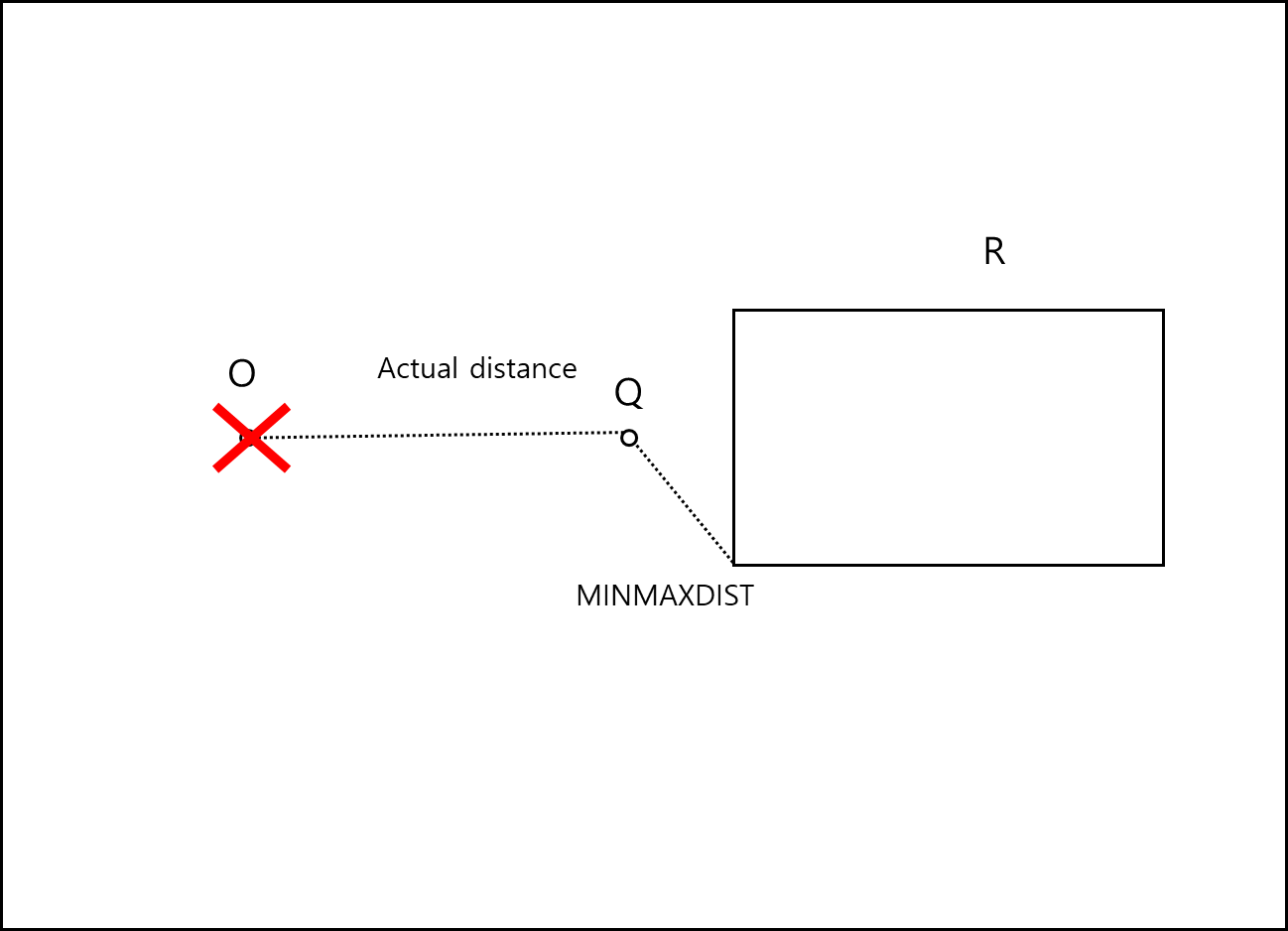
• 규칙 2. 상위 노드에서 하위 노드로 탐색시 : 어떤 MBB인 R에 대해서 실질 객체 O와의 거리가 R의 MINMAXDIST보다 크다면 객체 O는 탐색하지 않아도 된다.

  

• 규칙 3. 하위에서 상위노드로 다시 올라올시 : 어떤 MBB인 R에 대해서 실질 객체 O와의 거리가 R의 MINDIST 보다 작다면 R은 더 탐색하지 않아도 된다.

  

4) 알고리즘

위 가지치기 규칙을 기반으로 아래와 같은 알고리즘으로 탐색을 진행한다. 위에서 미리 언급했다 시피 R 트리의 각 노드는 우선순위 큐를 가지고 있으며 이를 ABL(Active Branch List)라고 한다. 여기서 우선순위 대상은 MINDIST가 작은게 가장 앞으로 와 있다.

1. 가장 가까운 거리를 갖고 있는 변수 NN를 무한으로 초기화한다.
2. 루트부터 시작하여 깊이 우선 방식으로 R 트리를 탐색한다. 각 인덱스 노드에서 모든 MBR을 정렬 기준(ordering metric)을 사용하여 정렬하고 ABL에 넣는다.
   • 각 노드는 쿼리에서 엔트리까지 MINDIST가 가장 작은 값이 앞에 오는 자체 ABL을 유지한다.
3. ABL에서 엔트리를 하나씩 꺼내서 가지치기 규칙 1과 2를 적용한 후에도 탐색 대상이라면 탐색한다.
4. ABL이 비어 있을 때까지 순서대로 MBB을 방문하여 알고리즘 3번 절차를 진행한다.
5. 리프 노드인 경우, 실제 거리를 계산하고, 지금까지 가장 가까운 이웃(NN)과 비교하고, 필요한 경우 업데이트한다.
6. 하위 노드에서 탐색을 다 하고 상위 노드로 복귀할 때 가지치기 규칙 3을 사용한다.
7. 탐색 중인 모든 ABL이 비어 있으면 변수 NN이 갖고 있는 현재 최근접을 반환한다.

5) 예시

아래의 그림을 보자.

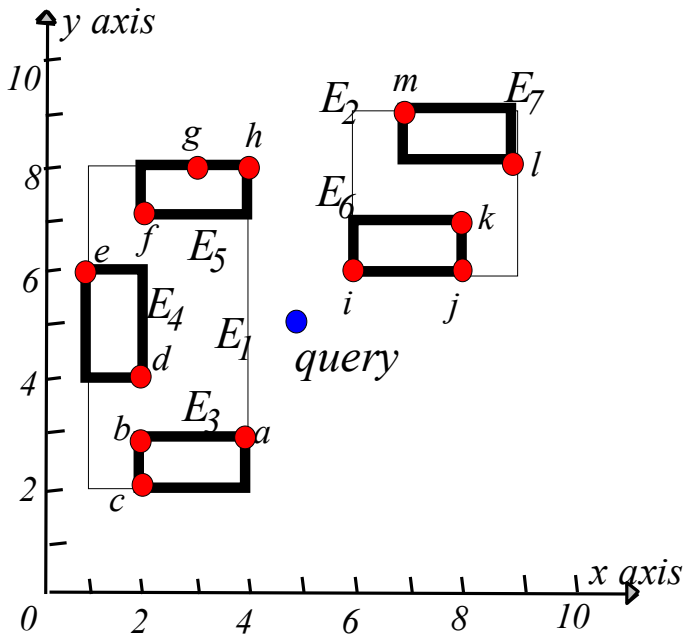
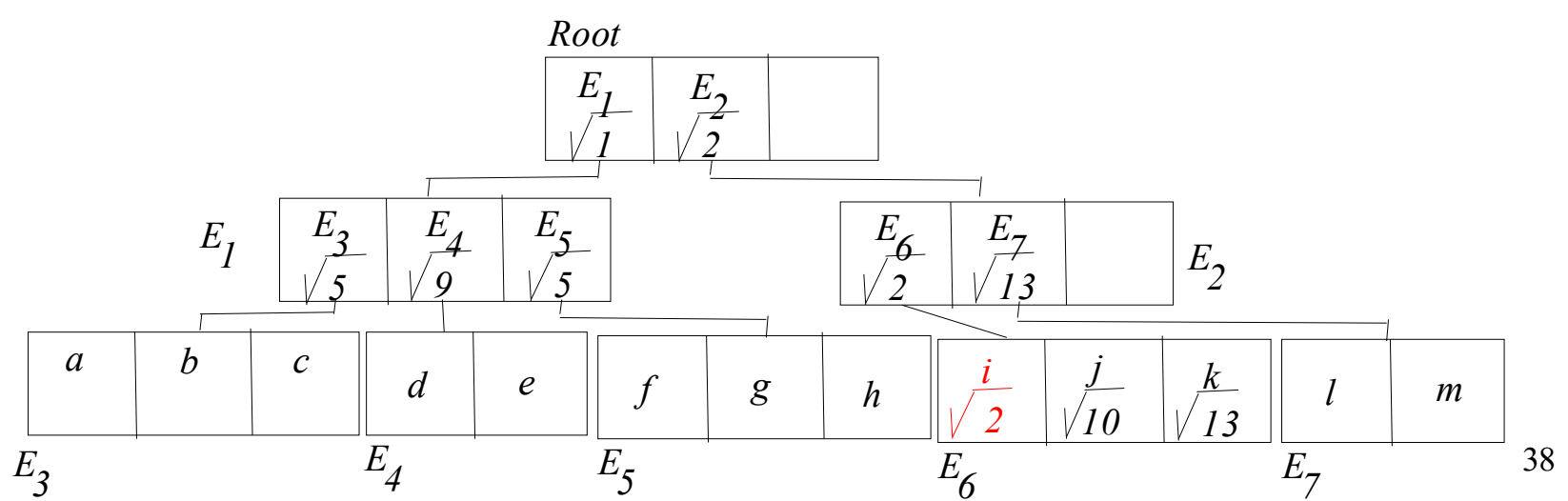
위와 같이 MBB가 구성이되어있고, 아래는 해당 모양대로 R 트리를 구성한 것이다. a~m은 실제 object 값이고, E1~E7은 해당 object를 MBB로 나눈 것들을 엔트리로 둔 것이다. N1~8은 각 트리의 노드들에 대해서 번호를 매긴 것이다.

기본적으로 DFS의 형태로 탐색을 하기 때문에 N1 노드부터 탐색한다.

1. E1은 QUERY로부터 거리가 1이고, E2는 거리가 루트 2이다. 따라서 E1부터 탐색한다.
2. E3, E4, E5가 있는데 MINDIST 거리만 보면 E3, E5가 같고, E4가 같으므로 E3, E5 ,E4 순으로 ABL에 들어간다.
3. E3에서 a,b,c가 있는데 a가 가장 가까우므로 a를 변수 NN은 a가 들어간다.
4. E5에서 d,e가 있는데 a가 더 가까우므로 a가 여전히 NN이다.
5. E4의 MINDIST는 a보다 길게 되었으므로 가지치기 된다.
6. 루트 노드로 올라가게 되고 E2를 탐색하게 된다.
7. E2는 E6, E7이 있는데 E6이 가까우므로 E6, E7순으로 ABL에 들어간다.
8. E6을 탐색하게 되고 i,j,k가 있는데 i가 가장 가깝고 a값보다 i가 더 가까우므로 NN은 i로 교체된다.
9. i의 거리가 E7의 MINDIST보다 짧으므로 가지치기된다.
10. 모든 ABL 큐가 비었으므로 NN인 i를 반환한다.

6) K-NN 확장

꼭 최근접 이웃 한개가 아닌 K개의 최근접 이웃이 필요할 수도 있다. 그렇다면 위 4)번 알고리즘을 아래와 같이 변경하면 된다.

1. 가장 작은 MINDIST 거리를 키로 하는 우선 순위 큐(NQ)를 만들고 거리가 무한인 값(실제론 자료형의 가장 큰 값)을 하나 넣어둔다.
2. 루트부터 시작하여 깊이 우선 방식으로 R 트리를 탐색한다. 각 인덱스 노드에서 모든 MBR을 정렬 기준(ordering metric)을 사용하여 정렬하고 ABL에 넣는다.
   • 각 노드는 MINDIST가 작은 값을 가진 엔트리가 가장 앞에 오는 자체 ABL을 유지한다.
3. ABL에 가지치기 규칙 1과 2를 적용한다.
4. ABL이 비어 있을 때까지 순서대로 MBR을 방문한다.
5. 리프 노드인 경우, 실제 거리를 계산하고, NQ의 루트인 지금까지 가장 가까운 이웃(NN)과 비교하고, 필요한 경우 NQ에 삽입한다.
6. 재귀에서 복귀할 때 가지치기 규칙 3을 사용한다.
7. ABL이 비어 있으면 필요한 K개 만큼 NQ에서 POP한다.

4. Best-First

1999년 Hellerstein과 Stonebraker가 제안한 방식으로 각 노드마다 ABL 큐가 있는 방식과 달리 글로벌 우선순위 큐 하나만 유지하는 방식이다.
Branch bound 방식이 DFS에 가까웠따면 Best-first 방식은 BFS에 가까운 방식이다.

1) 알고리즘

1. 글로벌 힙 H(priority queue)을 만드는데, 키는 각 엔트리(인덱스 엔트리 또는 객체)에 대한 MINDIST이다.
2. 초기화: 힙 H에 루트 엔트리(root)를 넣는다.
3. H가 비어있지 않다면 힙에서 MINDIST가 가장 작은 항목을 꺼낸다.
   • 꺼낸 항목이 인덱스 엔트리(내부 노드) 이면, 그 엔트리의 자식들(즉 자식 MBR들 또는 자식 엔트리들)을 힙에 삽입한다(각자 MINDIST 계산하여 키로 사용).
   • 꺼낸 항목이 객체(데이터 포인트) 이면, 이 객체를 최근접 이웃(NN) 으로 반환하고 알고리즘 종료.

2) 예시

3번에서 사용한 예시를 그대로 사용하도록 하겠다. 아래는 R트리이다.

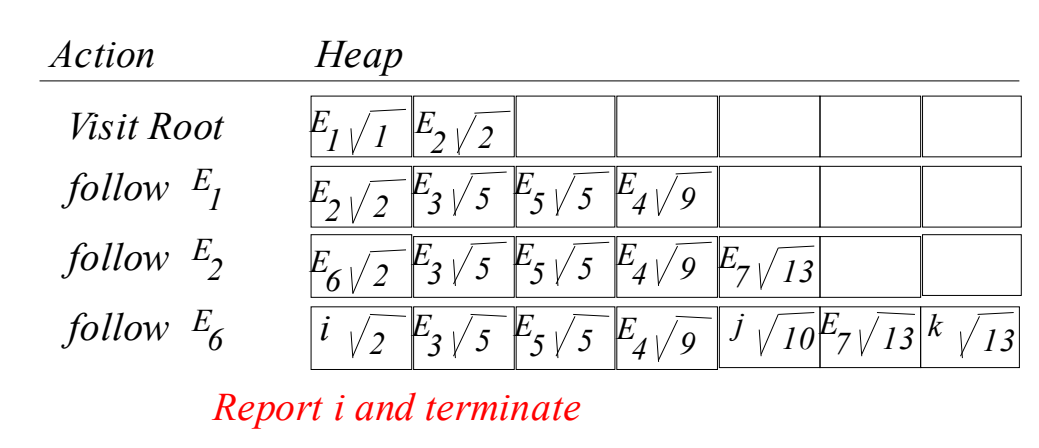
아래는 Global 우선 순위 큐의 엔트리 탐색별 전체 과정이다.

하나하나 차근차근 설명해보겠다.

1. 처음의 루트 노드를 탐색한다. E1,E2 중에 E1이 가까우므로 E1을 먼저 탐색한다.
2. Global 우선순위 큐(이하 GPQ)에서 E1을 빼고 E3, E4, E5를 GPQ에 넣고 MINDIST 거리순으로 정렬한다.
3. GBQ에서 E2가 가장 짧으므로 E2를 탐색한다. E2를 빼고 E6, E7을 GPQ에 넣고 MINDIST 순으로 정렬한다.
4. GBQ에서 E6가 가장 짧으므로 E6를 탐색하며 i,j,k object를 넣고 거리순으로 정렬한다.
5. 가장 앞에 있는게 i이므로 i를 반환하고 알고리즘을 종료한다.

3) K-NN 확장

Best-first는 K-NN 확장이 더 쉽다. K-NN 알고리즘은 아래와 같다.

1. 글로벌 힙 H(priority queue)을 만드는데, 키는 각 엔트리(인덱스 엔트리 또는 객체)에 대한 MINDIST이며 가장 작은 값을 가진 엔트리가 앞에 온다.
2. 초기화: 힙 H에 루트 엔트리(root)를 넣는다.
3. H가 비어있지 않다면 힙에서 MINDIST가 가장 작은 항목을 꺼낸다.
4. 그 항목이 인덱스 엔트리(내부 노드) 이면, 그 엔트리의 자식들(즉 자식 MBR들 또는 자식 엔트리들)을 힙에 삽입한다(각자 MINDIST 계산하여 키로 사용).
5. 그 항목이 객체(데이터 포인트) 이면, 이 객체를 최근접 이웃(NN) 중 하나로 반환한다. 이를 K개 반환할때까지 다시 반복한다.

5. Full Blown Algorithm

Full-Blown 알고리즘은 MINDIST를 기준으로 글로벌 우선순위 큐(H)를 유지하면서, 동시에 MINMAXDIST를 이용해 현재 가능한 상한(δ)을 점점 좁혀가며 MBR(엔트리)들을 적극적으로 가지치기하는 R-tree 기반의 branch-and-bound 방식이다.

1) 알고리즘

1. 글로벌 우선 순위 큐(priority queue)인 H를 만드는데, 키는 각 엔트리(인덱스 엔트리 또는 객체)에 대한 MINDIST이다.
2. 초기: H에 루트 엔트리를 삽입한다. 가장 작은 MINDIST 엔트리가 앞으로 온다.
3. δ는 현재 알고 있는 NN 거리의 상한으로 처음엔 무한대(+∞)이다.
4. H가 비어있지 않다면 힙에서 MINDIST가 최소인 항목인 e를 꺼낸다.
5. 만약 e가 객체(object)면 그 객체를 NN으로 반환하고 종료한다.
6. 그렇지 않고 e가 페이지(node)(인덱스 엔트리)면 페이지 PAGE(e) 안의 각 엔트리 se에 대해 MINDIST(q,se) ≤ δ 인 것들만 골라 H에 삽입한다.
7. 그리고 (가능하면) δ를 MINMAXDIST(q,se)로 감소시킨다(즉 δ←min(δ,MINMAXDIST(q,se)) ).
8. e가 객체가 나올때까지 반복한다.

2) K-NN 확장

이 역시 K-NN으로 확장이 된다. 몇 가지 세부사항만 달라지면 된다.

1. H에 루트 엔트리 넣고, R은 빈 구조. δ = +∞.
2. H가 비어있지 않고 (R.size < K) OR (min_MINDIST(H) ≤ δ) 인 동안 다음을 반복:
   • H에서 e = 최소 MINDIST 항목을 꺼낸다.
   • 만약 e가 리프의 객체(object)라면:
   • 정확 거리 d = dist(q, e) 계산.
   • R에 삽입:
     • 만약 R.size < K → 넣기.
     • 아니면 d < worst(R) (max-heap의 루트) 이면 루트 제거하고 넣기.
   • δ = worst(R) (R.size==K이면 k번째 거리, 아니면 +∞) - 만약 e가 인덱스 엔트리(노드/페이지)라면:
   • 페이지(e)의 각 엔트리 se에 대해 if MINDIST(q,se) ≤ δ이면 se를 H에 삽입.
   • (선택적) 삽입 시 MINMAXDIST(q,se) 값이 현재 δ보다 작으면 δ ← MINMAXDIST(q,se) (원본 알고리즘의 최적화).
3. 종료: H 비어있거나 (R.size == K && min_MINDIST(H) > δ). 반환: R의 원소들(가장 작은 거리 순으로 정렬해서 반환).

※ Branch-bound vs Best-first

Best-first는 큰 한 개의 글로벌 큐를 유지한다. 이는 글로벌 큐가 너무 커지면 메모리 문제로 인해 성능 저하를 초래한다. 반면 branch-bound 방식은 각 node별 abl을 유지하기 때문에 메모리 문제가 비교적 덜한 편이다. 물론 알고리즘 자체는 best-first가 좀 더 최적이긴 하지만 위와 같은 이유로 메모리가 제한된 모바일 같은 경우에는 branch-bound 방식을 많이 차용한다.

6. Closest Pair Query

두 개의 R 트리가 있다고 할 때 각 트리에서 한 점씩을 선택할 때 각 점 간의 거리가 가장 가까운 한 쌍을 반환하는 쿼리이다.
일단 두 개의 R트리인 A와 B의 높이가 같다고 가정하겠다. NN 쿼리 알고리즘과 기본적으로 비슷한데, 두 개의 MBB 간에 MINDIST와 MINMAXDIST는 아래와 같이 정의하겠다.

• MINDIST : MBB A에서 MBB B까지의 가장 짧은 거리
• MINMAXDIST : MBB A에서 MBB B의 각 4개의 변 중에 가장 가까운 변에서 가장 먼 점과의 거리

1) 기본적인 알고리즘

1. 작은 값이 먼저인 우선순위 큐 H에 MINDIST를 키로 A루트-B루트 쌍을 넣는다.
2. H에서 MINDIST가 가장 작은 쌍 (eR, eS)를 꺼낸다.
3. 만약 (eR, eS)가 둘 다 실제 객체(leaf) 의 쌍이면, 이 쌍이 현재 가장 가까운 쌍(=CP)이므로 반환한다.
4. 그렇지 않다면 (즉 둘 중 적어도 하나가 인덱스 엔트리라면), 해당 엔트리들을 자식 엔트리들의 모든 조합으로 확장하여 (자식a, 자식b) 쌍을 H에 삽입한다(삽입 시 그 쌍의 MINDIST로 우선순위 부여).

2) Full-blown 알고리즘

기본적인 알고리즘에서 개선하는 방식으로 이전 NN Full-blown 알고리즘을 확장한 형태이다. 현재 발견된 최소거리 $\delta$는 유지하고 자식쌍을 삽입할때 MINDIST가 $\delta$ 이하인 경우에만 삽입해 불필요한 확장을 줄인다. 여기서 $\delta$는 어떤 쌍의 MINMAXDIST값 보다 더 클 경우 $\delta$값을 해당 MINMAXDIST로 바꾼다.

7. Close Pair Query

어떤 임계값 $\alpha$ 가 주어졌을 때 R트리 A와 B의 두 점의 거리가 $\alpha$ 미만인 쌍을 모두 찾아서 반환하는 것이다.

1) 알고리즘

1. 글로벌 Stack S에 A루트-B루트 쌍을 PUSH
2. S가 빌 때까지 아래의 작업을 진행한다.
   • S에서 쌍 하나를 POP하고 해당 쌍(A,B)의 자식을 가져온다.
   • 인덱스 엔트리든 실제 값이든 대상 엔트리의 MBB가 MINDIST(MBB_a,MBB_b) < $\alpha$ 인지 체크한다. 아니라면 가지치기 해버리고, 맞다면 아래의 절차를 따른다.
   • 인덱스 엔트리면 S에 MBB_a와 MBB_b 쌍을 넣는다. (다음 루프에서 해당 값들의 자식이 검색됨)
   • 오브젝트에 대한 MBB라면 실제 오브젝트에 대한 거리를 계산 후 정답 큐에 넣는다.
3. 정답 큐를 반환한다.

참고자료

• Shashi Shekhar and Sanjay Chawla, Spatial Databases: A Tour, Prentice Hall, 2003
• P. RIigaux, M. Scholl, and A. Voisard, SPATIAL DATABASES With Application to GIS, Morgan Kaufmann Publishers, 2002