Post

공간 데이터 베이스 - RNN(Reverse nearest neighbor)

Posted Updated
By Blake Woo 15 min read

RNN(Reverse nearest neighbor)

1. 개요

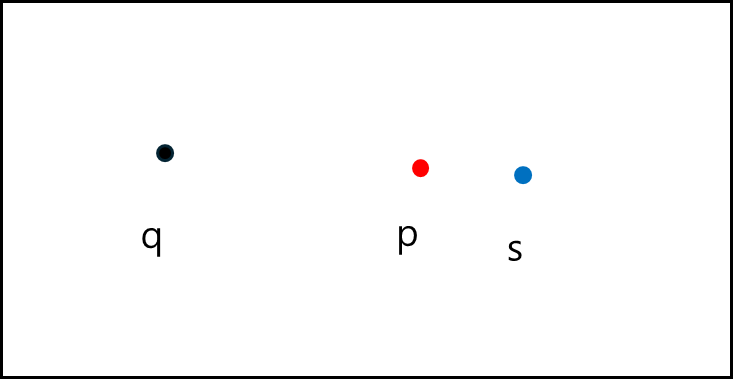
RNN은 Query q에 대해 어떤 점 p가 p의 최근접이 q인 경우 p를 q의 역최근접 이웃으로 간주하는 개념으로, 직관적으로 q가 특정 점들의 NN이 되는 집합을 찾는 문제를 말한다.

q의 가장 최근접이 p일 때 q 역시 p의 가장 최근접이 아닌가 하고 그냥 언뜻 생각하면 그렇게 생각할 수 있지만 꼭 역이 성립하지는 않는다.

img.png

위와 같은 경우에는 q의 가장 최근접 이웃은 p이지만 p의 최근접 이웃은 s이다.

2. Precomputing

1) KM00

KORN과 Muthukrishnan이 00년도에 냈다고 KM00이라고 붙은 것 같다.
이 방법을 정리하자면 굉장히 간단하다.

모든 데이터점 p에 대해 NN(p)을 사전 계산하고 이를 기반으로 p의 근방을 원(vicinity circle)으로 표현한 뒤, 모든 원의 MBR을 R-tree(RNN-tree)에 색인하여 q를 포함하는 원들의 집합을 RNN(q)로 반환한다. 두 개의 트리(RNN-tree와 데이터 R-tree)가 필요하다는 점이 구현·유지 비용으로 작용한다.

2) YL01

Congjun Yang과 King-Ip Lin이 01년도에 만들었다고 YL01이다.
KM00과 같이 별도의 RNN-tree를 유지하는 것까지는 같으나 구조가 다르다.

논문이 제안하는 RdNN-tree는 잎 노드에 각 데이터점 p의 비서티 원(중심 p, 반경 = NN(p)까지의 거리)을 저장하고, 내부 노드는 하위 원들의 최소 경계 사각형(MBR)들을 보관한다. 이렇게 하면 질의 시 점 위치 질의를 통해 q를 포함할 수 있는 원들의 후보 집합을 신속히 결정할 수 있으며, 원의 유지·갱신도 R-tree 연산으로 처리 가능하다.

3. Filter/refinement

1) SAA

a. 필터 단계

질의점 q를 중심으로 공간을 6개의 동일 각도(60°) 영역 S₁, S₂, …, S₆로 분할하고, 각 영역 Sᵢ 내에서 q에 가장 가까운 점(NN(q) in Sᵢ)을 찾아 후보 키 집합에 추가한다. 이렇게 하면 최대 6개의 후보 점이 수집되며, 사전에 모든 점의 NN을 계산·저장할 필요가 없어 KM00 대비 갱신 부담이 줄어든다.

b. 정제

각 후보 p에 대해 다음 두 조건 중 하나가 성립하는지 확인한다.

  • p ∈ RNN(q): p의 실제 최근접 이웃이 q이므로 p를 결과에 포함한다.
  • 해당 영역 Sᵢ에 RNN 없음: 영역 Sᵢ 내에 q를 최근접 이웃으로 갖는 점이 존재하지 않음을 확인하고, 해당 후보를 기각하거나 다른 후보를 결과로 확정한다.

c. 단점

영역 수가 차원에 대해 지수적으로 증가한다. 이 말은 2차원에서는 6개 영역이 충분하지만, 3차원 이상으로 확장 시 필요한 영역 개수가 급증하여 후보 탐색·비교 비용이 폭발적으로 늘어나므로 고차원 데이터에 적용하기 어렵다.

2) SFT

a. 필터

  1. 먼저 질의점 q에 대해 k-최근접 이웃(kNN)을 계산하여 q 주변의 k개의 최근접 이웃 점들을 후보(key) 집합에 추가한다.
  2. 일반적으로 이 k-NN은 R-tree와 같은 공간 인덱스를 이용해 수행하며, k값은 임의로 정해진다.

b. 정제

수집한 후보 p들끼리 서로를 거르며 일부 후보를 제거할 수 있다. 예를 들어, 해당 점이 다른 후보에 비해 q에서 멀리 떨어져 있을 경우 후보에서 제외되는 방식이다. 남은 후보에 대해, 해당 점이 정말로 RNN(q)에 포함되는지 판정해야 한다. 이를 위해 보통 불리언 범위 질의(Boolean range query)를 수행한다. 불리언 범위 질의란 후보 p에 대해, q와 p 사이의 거리가, 다른 어떤 데이터점 p′ 와 p의 거리보다 더 작은지 점검하는 것이다. 실제로는, p를 중심으로 q까지의 거리만큼의 원(또는 영역)을 그려 두고, 그 원 내부(p에서 q까지의 거리보다 더 가까운 거리에) 다른 데이터점이 있다면 p는 제외된다.

c. 장단점 및 한계

  • 불리언 범위 질의 과정에서, 처음 데이터점을 찾거나 노드 MBR 한 변 전체가 원 안에 들어오면 질의를 조기 종료할 수 있다.
  • k값이 작을 경우 실제 정답을 포함하지 못하는 경우가 발생할 수 있고, 반대로 k를 크게 잡으면 후보 수가 불필요하게 많아져 성능이 저하될 수 있다.

4. TPL

모든 데이터는 R-tree에 색인되어 있고, RNN 후보 추출 및 검증을 위해 관리되는 두 가지 집합을 정의한다(필터 후보 집합 Scnd와 정제 후보 집합)

1) 필터

R-tree의 루트에서부터 우선순위 기반(힙)으로 순차적으로 노드를 탐색한다. 각 노드 또는 포인트에 대해 TPL의 가지치기 조건(예: 반평면 또는 MBR 근사 등)을 적용하여, 불필요한 노드·포인트를 건너뛴다. 후보 포인트가 필터 집합에 추가된다.

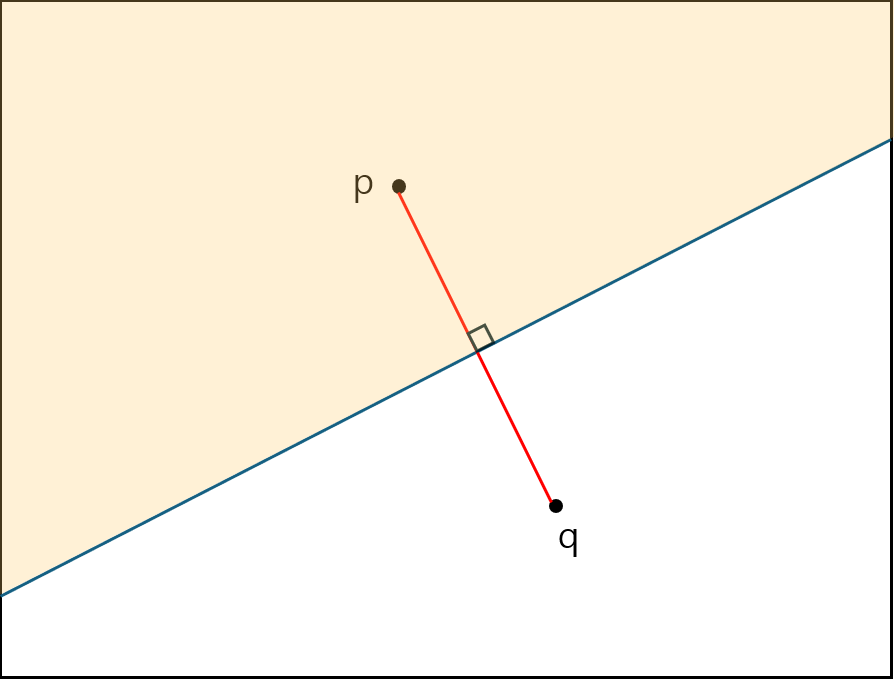
a. 반평면 가지치기

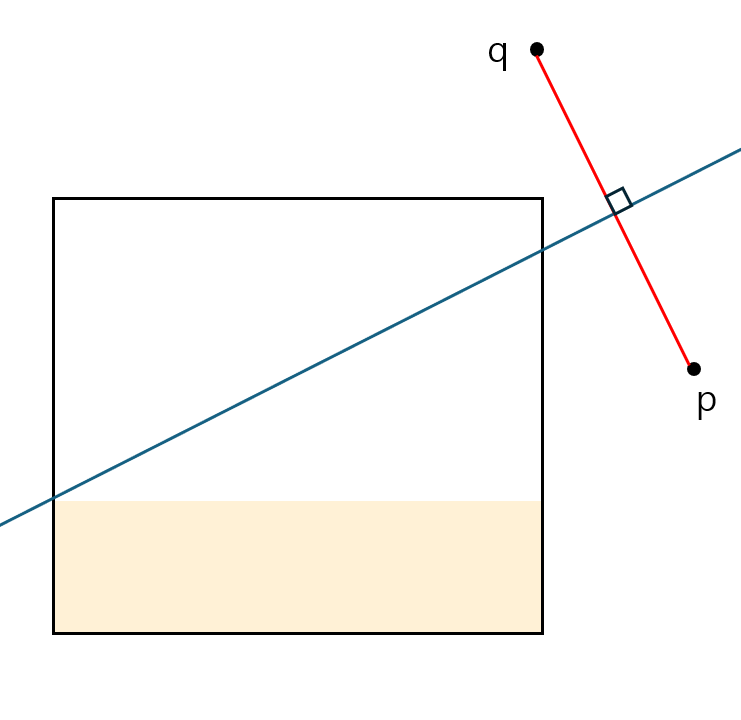
query와 어떤 점 p가 최 근접이라면 p와 그은 선분을 이등분 한 점에서 직각으로 선을 그었을 때 절반만큼의 영역에 속한 점은 q에 가까울 수 없다.

img.png

그 다음 가까운 점에서도 마찬 가지이다.

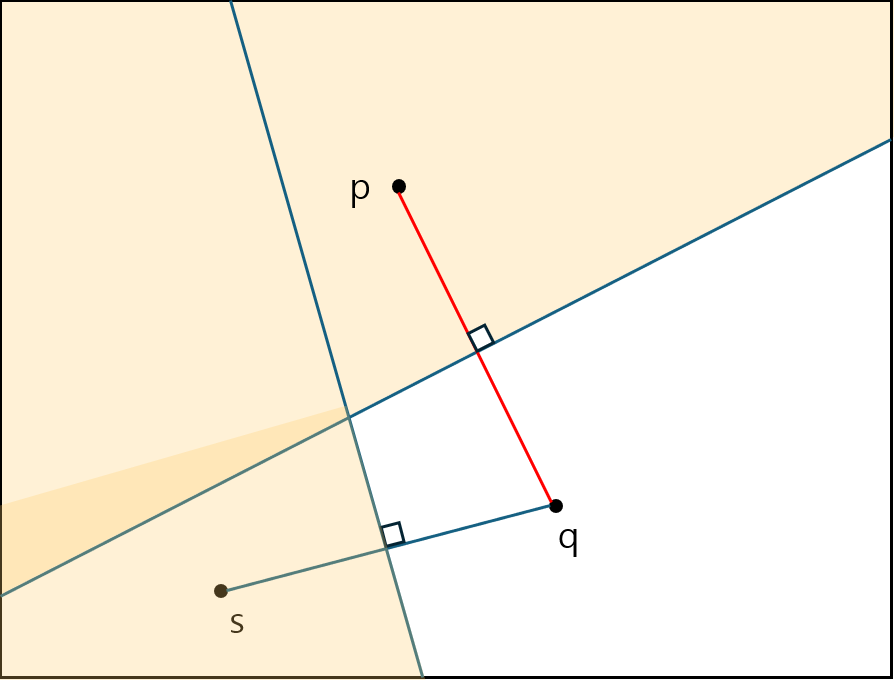
img_1.png

위와 같이 가지치기를 하는데, 만약 특정 MBR이 걸쳐있게 된다면 이 역시 아래와 같이 가지치기 된다.

img_2.png

b. MBR 근사 가지치기

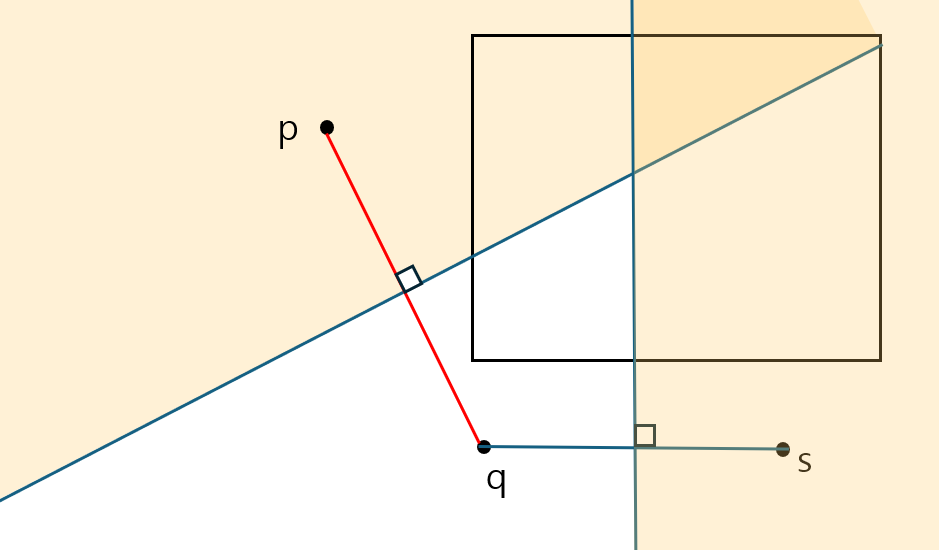
MBR 역시 특정 각도로 가지치기 될 경우에 가지치기 된 MBR을 그대로 다루는 건 매우 어렵다.
이는 다각형의 형태가 되기 때문이다. 따라서 MBR이 가지치기 된 경우 아래와 같이 근사하여 MBR을 축소하는 방법으로 가지치기를 하여 사용한다.

img_3.png

주황색 음영처리가 된 부분을 잘라내면 기존 MBR의 사각형 형태는 유지하되 가지치기 되면 안되는 부분까지 모두 포함하기 때문에 이런식으로 근사 가지치기를 한다.

2) 정제

후보 집합(Scnd)에서 실제로 역최근접이웃이 될 수 있는지를 판정하기 위해 정제 집합(Srfn)을 활용한다.
포인트 $p$가 실제로 $q$의 역최근접이웃이 되려면, $p$의 실제 최근접 이웃이 $q$여야 하며, 다른 후보나 노드에 의해 가로막히지 않아야 한다.
만약 $p$가 다른 후보 포인트들(Prfn) 중 어느 것보다 $q$에서 멀거나, 정제 노드들(Nrfn)에 의해 잠재적으로 가로막힐 가능성이 있다면, $p$는 제거된다.
$p$에 대해 모든 정제 후보가 충분히 검증되면, 실제 RNN 결과로 확정된다.
mindist(최소거리) 기준으로 추가 방문이 필요하면, 힙에서 더 노드를 꺼내 정제 단계를 반복한다.

3) 예시

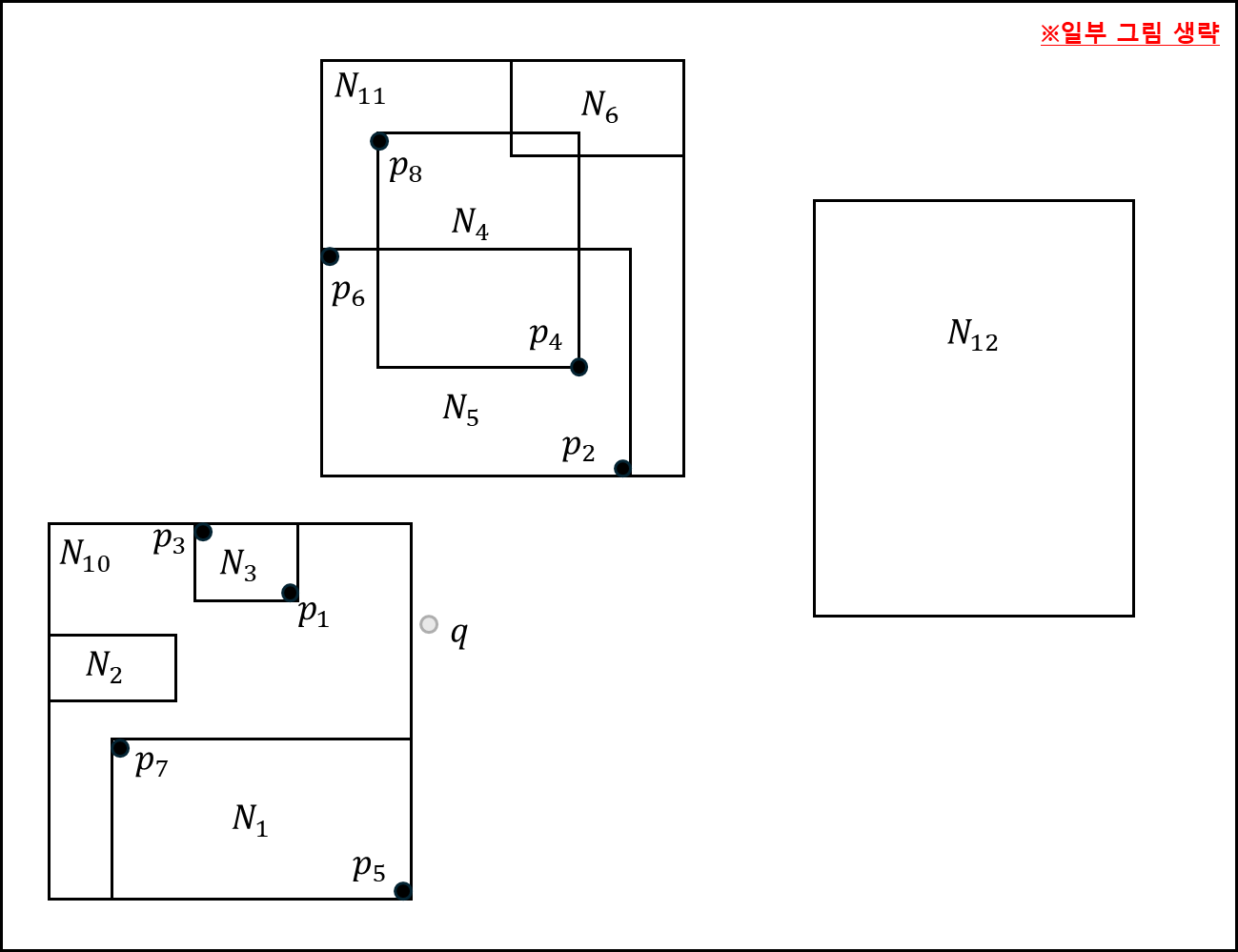
아래와 같은 공간 정보가 있다.

img.png

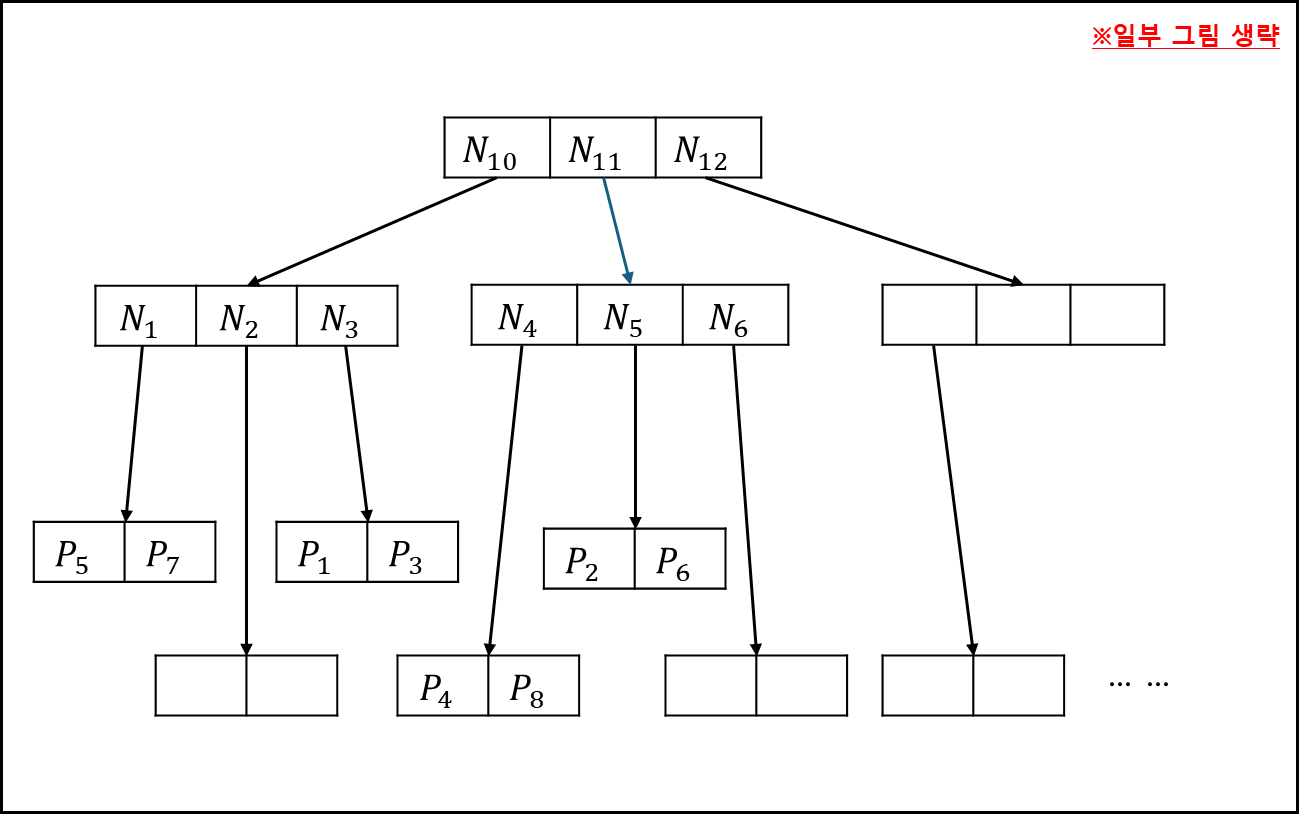
이를 R-tree로 나타내면 아래와 같다.

img_1.png

이를 탐색하는 순서를 표로 나타내면 아래와 같다.

a. Filter step

작업우선순위큐ScndSrfn
루트노드방문$N_{10},N_{11},N_{12}$
$N_{10}$ 노드 방문$N_{3},N_{11},N_{2},N_{1},N_{12}$
$N_{3}$ 노드 방문$N_{11},N_{2},N_{1},N_{12}$$p_{1}$$p_{3}$
$N_{11}$ 노드 방문$N_{5},N_{2},N_{1},N_{12}$$p_{1}$$p_{3},N_{4},N_{6}$
$N_{5}$ 노드 방문$N_{2},N_{1},N_{12}$$p_{1},p_{2}$$p_{3},N_{4},N_{6},p_{6}$
$N_{1}$ 노드 방문$N_{12}$$p_{1},p_{2},p_{5}$$p_{3},N_{4},N_{6},p_{6},N_{2},p_{7}$
$p_{1},p_{2},p_{5}$$p_{3},N_{4},N_{6},p_{6},N_{2},p_{7},N_{12}$
  1. 처음에는 루트 노드를 확인한다. N10과 N11, N12를 Mindist 기준으로 우선순위 큐에 넣는다.
  2. N10을 확인하면 안에 N1,N2,N3이 있는데 이를 우선 순위 큐에 넣는다.
  3. 가장 가까운 N3를 체크하면 점 p1과 p3가 있는데, p1이 p3보다 더 가깝다. 더 가까운 값이 나오기 전까지는 p1이 가장 가까우므로 해당 p1을 기준으로 반평면 가지치기를 한다.
    이 과정에서 p3는 가지치기가 되어 Srfn에 들어가고 Scnd에는 p1이 들어간다.
  4. N11을 확인하면 N4,N5,N6가 있다. 하지만 N4와 N6는 가지치기 반평면에 포함되므로 Srfn으로 포함되고, N5는 애매하게 걸치기 때문에 우선 순위 큐에 들어가게된다.
  5. N5를 꺼내서 확인하면 p2,p6를 볼 수 있다. p6보다 p2가 가깝고, 가지치기 반평면에 포함되어있지 않으므로 p2를 Scnd에 포함하고 Srfn에 p6를 넣는다.
  6. N2는 가지치기 반평면에 포함되므로 Srfn에 넣어버리고, N1을 확인한다. p7은 가지치기되므로 Srfn에 넣고, p5는 Scnd에 포함한다.
  7. N12는 가지치기되어 Srfn에 들어간다.

b. Refinement step

작업ScndSrfn실제 값
$p_{1},p_{2},p_{5}$$p_{3},N_{4},N_{6},p_{6},N_{2},p_{7},N_{12}$
$p_{1}$ 후보 삭제$p_{2},p_{5}$$N_{4},N_{6},N_{2},N_{12}$
$p_{5}$ 확정$p_{2}$$N_{4},N_{6},N_{2},N_{12}$$p_{5}$
$N_{2},N_{6}$ 삭제$p_{2}$$N_{4},N_{12}$$p_{5}$
$N_{4}$ 접근$p_{2}$$p_{4},p_{8},N_{4},N_{12}$$p_{5}$
$p_{2}$ 후보 삭제$N_{12}$$p_{5}$
  1. Scnd에 있는 후보군을 하나씩 체크한다. p1,p2,p5의 각각 점과 q까지의 거리를 반지름으로 하는 원을 그렸을 때 해당 원 안에 다른 점이 있다면
    해당 점은 제거한다. p1의 경우 p3가 포함되므로 후보군에서 제거한다.
  2. p5는 반경 내에 아무것도 포함되지 않으므로 실제 값이다.
  3. Srfn에 N2와 N6가 점의 반경에 포함되지 않으므로 완전 제거한다. 다른 점을 고려할때 이 MBR은 고려하지 않아도 된다.
  4. N4를 Srfn에 꺼내서 확인한다. 안에 p4와 p8가 있다. 이 값을 Srfn에 포함한다.
  5. p2의 반경에 p4가 포함되어있으므로 p2를 제거한다.
  6. 최종 RNN은 p5이다.

참고자료

  • Shashi Shekhar and Sanjay Chawla, Spatial Databases: A Tour, Prentice Hall, 2003
  • P. RIigaux, M. Scholl, and A. Voisard, SPATIAL DATABASES With Application to GIS, Morgan Kaufmann Publishers, 2002
  • Korn, Flip, and S., Muthukrishnan. “Influence sets based on reverse nearest neighbor queries.” . In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data (pp. 201–212). Association for Computing Machinery, 2000.
  • Tao, Yufei, Dimitris, Papadias, and Xiang, Lian. “Reverse kNN search in arbitrary dimensionality.” . In Proceedings of the Thirtieth International Conference on Very Large Data Bases - Volume 30 (pp. 744–755). VLDB Endowment, 2004.
Database
Computer science Database Spacial Database RNN
This post is licensed under CC BY 4.0 by the author.