공간 데이터 베이스 - Road Network

Road Network

1. 개요

이전까지 공간 데이터 베이스에 관련된 포스팅은 직선거리에 대한 내용이었다.
하지만 실제 우리가 거리와 공간에 대해서 질의할 때 얻는 답변은 실제로 우리가 가고자하는 곳에 어떤 도로나 길을 타고 갔을 때 얼마나 가야 가장 가깝게 도착할 수 있는지 등에 대한 내용이다.

2. Graph Modeling of Road Network

길에 대해서 탐색하기에 앞서, 어떤 곳으로 가는데 길 정보가 필요하기 때문에 이를 위해서는 별도로 도로를 모델링해서 탐색 정보에 포함해야한다.
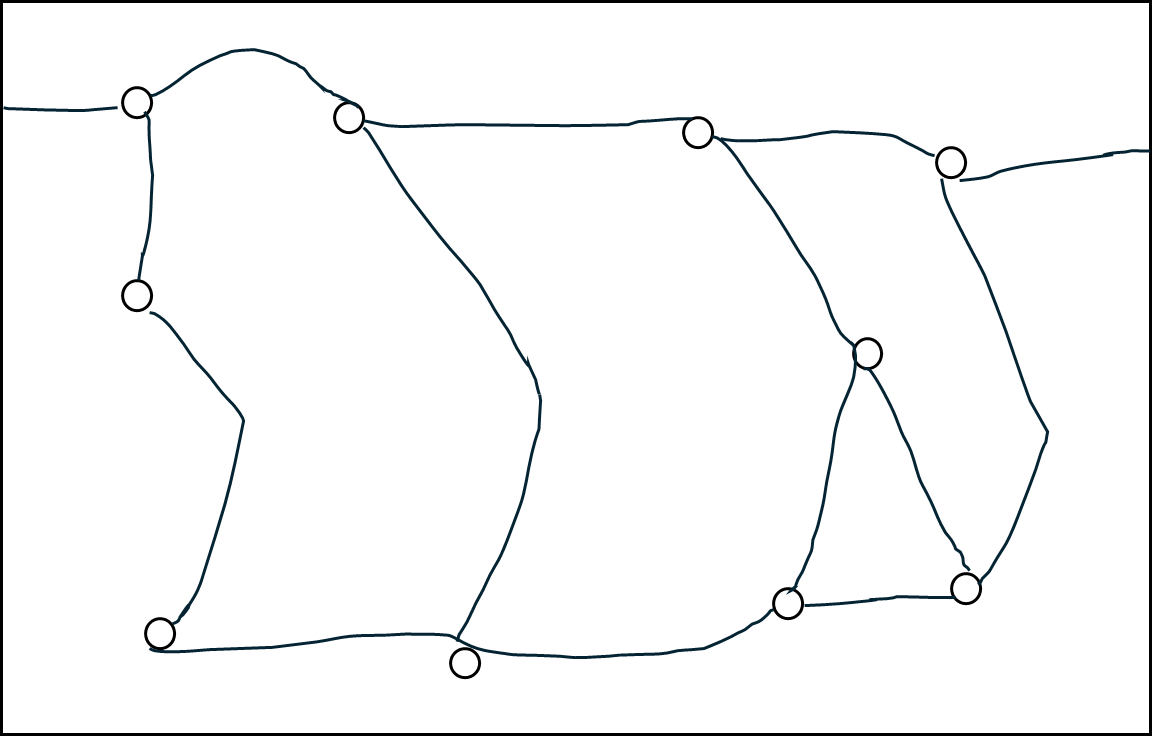
이를 Road Network라고 한다. 아래의 그림을 보자.

이렇게 생긴 지도가 있다고 해보자. 각 원은 어떤 건물이나 목적지가 될 수 있고 선은 실제 도로를 그린거라고 해보자. 하지만 이대로 쓰기는 어렵다. 좀 더 계산하기 편하게 아래와 같이 모델링 할 수 있다.

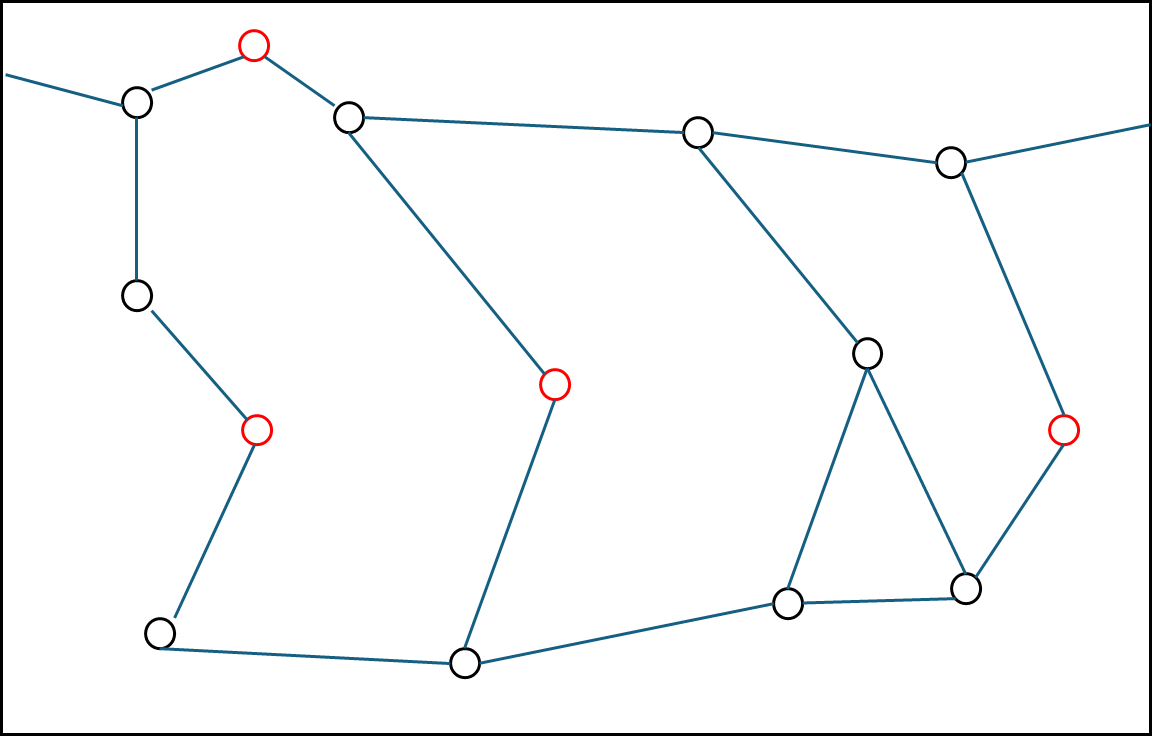
직선만으로 표현하면 거리를 재는데 용이해진다. 따라서 꺾이는 부분에는 빨간점으로 임의의 node를 선정해서 모델링했다.
위와 같이 모델링하면 사용하기 편하다. 아래는 어떻게 Road Network를 그래프로 모델링하는지에 대한 내용이다.

1. 엣지에 저장된 거리: 그래프의 단일 엣지는 실제 도로 구간 하나를 나타내고, 그 엣지의 weight로 길이(혹은 주행 시간)를 기록한다.
   예: 교차로 A–B를 잇는 도로 길이가 120 m이면 그 엣지의 $d_{N}(A,B)=120$ (또는 시간 기준 가중치).

2. 비직접 연결 노드의 거리 = 최단 경로 길이: 노드 A와 C가 직접 연결되어 있지 않다면 A→C 거리는 A→…→C 로 연결된 경로들 중 가장 짧은(또는 최소 비용) 경로 길이다. 즉 그래프 최단경로 개념(다익스트라 등)인 셈이다.

3. 비대칭성 예시: 일방통행 도로가 있으면 A→B로 갈 수 있지만 B→A는 다른 길(우회)로 가야 하므로 거리/시간이 달라진다.
   예를 들어 A→B는 100 m, 하지만 B→A는 일방통행이라 우회해 600 m라면 $d_{N}(A,B)=100\ne d_{N}(B,A)=600$ 으로 환산한다.

4. 유클리드 하한 성질(직선거리는 항상 더 작거나 같다): 실제 도로로 이동하는 거리는 직선보다 같거나 길다(도로가 직선으로 이어지지 않거나 우회가 있기 때문). 따라서 직선거리로부터 네트워크 거리의 하한을 얻을 수 있다. 이 성질이 후보 필터링(예: RER, IER)에서 핵심으로 사용된다 — “직선 거리가 반경 e를 넘으면 실제 도로로는 그보다 더 멀 것이다” 라는 안전한 배제 규칙을 만들 수 있다.

3. Nearest Neighbor Queries in Spatial Network DB

1) IER(Incremental Euclidean Restrictions)

a. 알고리즘

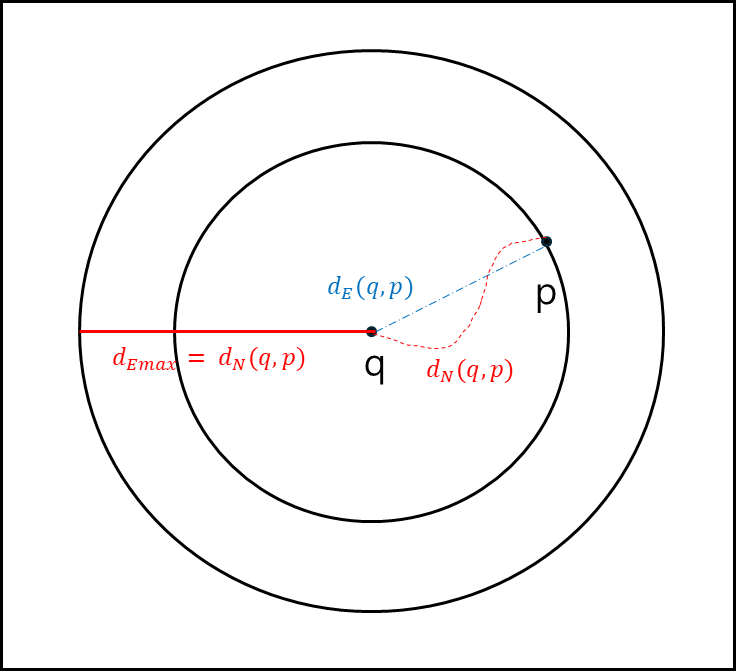
어떤 점 q에서 직선 거리로 가장 가까운 점 p가 있을 때 p에 대해 직선 거리를 $d_{e}(q,p)$, q와 p의 네트워크상의 실제 거리를 $d_{N}(q,p)$ 라고 하고 $d_{N}(q,p)$을 반지름으로 q에서 원을 그릴때 아래와 같이 된다.

이 반지름을 $d_{Emax}$라고 하며 $d_{N}(q,p)$와 같은 값이다.
어떤 점 q 로부터 Road Network 상에서 가장 가까운 노드를 찾고 싶을 때 위와 같이 접근한다.
유클리드 거리는 항상 네트워크 경로 거리의 하한이므로 유클리드 거리가 현재 최단 네트워크 거리보다 크거나 같으면 그 후보 및 그 뒤 후보들은 더 가깝지 않다.

다음은 알고리즘을 차례로 설명한 것이다.

1. q로 부터 유클리드 거리(직선거리)로 가장 가까운 점(n) 하나를 찾는다.
2. q와 n의 네트워크 거리를 구한다.( $d_{N}(q,n)$)
3. $d_{N}(q,n)$를 $d_{Emax}$ 로 설정한다.
4. 이후 다른 노드들을 탐색하는데 다른 노드를 nk라고 할때 $d_{N}(q,nk) < d_{N}(q,n)$ 이면 $d_{Emax} = d_{N}(q,nk)$ 로 세팅한다.
5. 노드를 모두 탐색했다면 $d_{Emax}$로 선정된 노드를 반환하고 알고리즘을 종료한다.

b.장점/단점

1. 유클리드 거리로 후보를 잘 걸러낼 수 있으면 효율적(짧은 후보 목록만 네트워크 거리 계산)이다.
2. 그러나 유클리드-네트워크 순서가 매우 불일치하면(유클리드 가까움이 네트워크에서 멀 수 있음) 많은 후보를 검사해야 한다.

c. K-NN 확장

위 과정을 k개 답을 찾을 때까지 반복하고, $d_{N}max$는 k번째로 큰(가장 먼) 네트워크 거리로 갱신하여 추가 후보를 배제한다

1. 모든 노드를 쿼리점 q로부터 유클리드 거리 순으로 정렬하거나 혹은 유클리드 NN을 반복 추출할 수 있는 구조(R-tree라던지)를 사용해서 K개를 뽑아서 배열에 넣는다. 이 배열을 NN_Arr이라고 하겠다.
2. NN_Arr의 후보를 하나씩 꺼내 실제 네트워크 최단경로 거리 dN를 계산하고 이를 배열 dN_Arr에 넣는다.
3. dN_Arr을 네트워크 거리가 짧은 순으로 정렬한다. 정렬된 배열에서 가장 끝에 있는 값, 실제거리로 볼때 K번째 점을 선택해서 $d_{Emax}$ 값으로 지정하고 네트워크 거리를 넣는다.
4. 유클리드 거리로 K+1번째로 가까운 점을 꺼내서 실제 네트워크 거리를 $d_{Emax}$과 비교하고, $d_{Emax}$값 보다 짧다면 k번째 점을 제거하고 k+1번째 점을 dN_Arr에 넣는다.
5. dN_Arr에서 가장 네트워크 거리가 먼 점을 $Emax$로 선정하고 실제 네트워크 거리를 $d_{Emax}$로 지정한다.
6. 뽑아낸 노드의 직선거리가 $d_{Emax}$보다 길다면 반복문을 종료한다.

2) INE(Incremental Network Expansion)

IER의 경우 간편하긴 한데, 까보면 $d_{Emax}$와 $d_{E}$ 값의 차이가 크면 그 사이를 탐색해야하는 IER의 경우에는 계산량이 늘어날 수밖에 없다.
이러한 문제로 인해 새로운 방식이 나왔다. 이 방식은 Road network상에서 조금씩 확장해가며 탐색하는 방식이다.

a. 알고리즘

설명이 좀 어려우므로 아래의 예시를 보면서 설명하겠다.

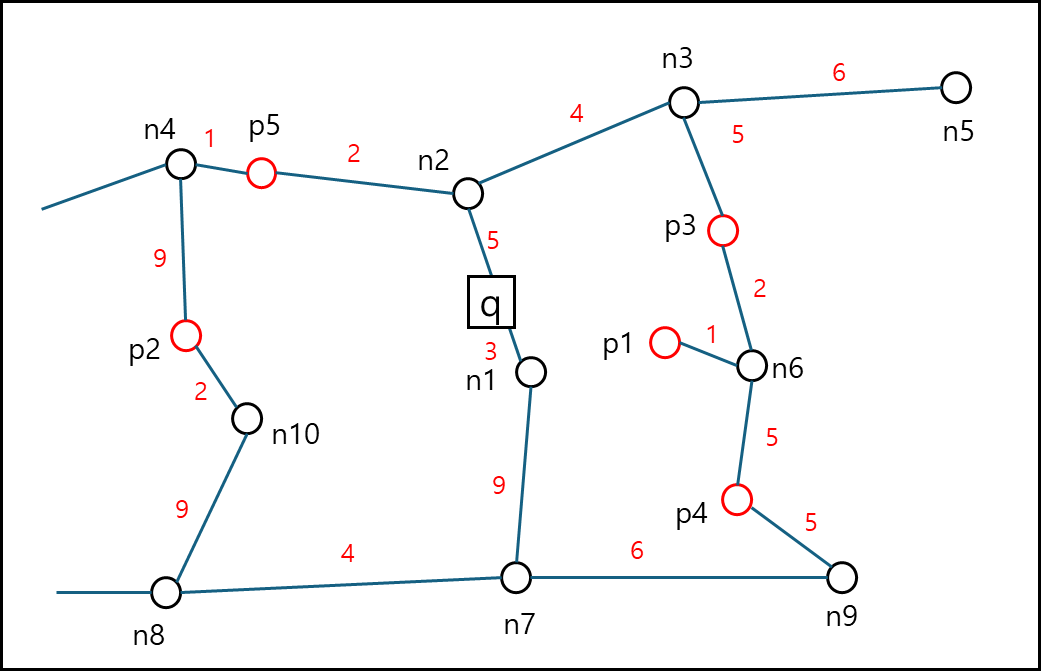
가령 어떤 위치 q에서 가장 가까운 호텔(1NN)을 찾고 싶다고 하자. 위 그래프에서 빨간 동그라미는 호텔이고 검은 동그라미는 경유지라고 하면 아래의 순서대로 찾게 된다.
우선순위 Queue 하나를 선언하되, 거리가 가까운 점이 먼저오는 Queue이다.

1. 처음에 $d_{Nmax} = $ ∞로 초기화한다.
2. q점에서 접근 가능한 점을 찾아서 Queue에 넣는다. 각 원소는 (점이름, 거리)으로 표기한다. : <(n1, 3),(n2, 5)>
3. Queue에서 하나 꺼낸다. n1에서 접근 가능한 점을 찾아서 n1까지의 거리를 더한 뒤에 Queue에 다시 넣는다. : <(n2, 5),(n7, 12)>
4. Queue에서 하나 꺼낸다. n2에서 접근 가능한 점을 찾아서 n2까지의 거리를 더한 뒤에 Queue에 다시 넣는다. : <(n4, 8),(n3, 9),(n7, 12)>
5. n4까지 가는 길에 호텔 하나(p5)가 있다. p5까지의 거리는 7로 당장 가까운 점은 p5라고 볼수 있으나 확실하지는 않다. 따라서 p5를 후보로 선정하고, $d_{Nmax} = 7$로 세팅하고 계속 진행한다.
6. Queue를 확인한다. 해당 Queue에 모든 Node까지의 거리가 $d_{Nmax} = 7$ 보다 크다. 따라서 p5를 반환하고 종료한다.

위의 경우에는 가장 가까운 것만 찾았기 때문에 첫번째 후보군에서 dmax를 선정했지만, 만약 K개를 뽑고 싶을 경우 K번째 후보가 추가되었을때 가장 긴 거리를 가진 p값으로 dmax를 지정하면 된다.

b. 장점/단점

1. 유클리드 근사에 의존하지 않으므로 유클리드-네트워크가 크게 어긋나는 상황에서 우수.
2. 그러나 네트워크 전체를 많이 탐색해야 할 수 있어 비용이 클 수 있음(특히 고밀도 네트워크에서).

4. Range Queries in SNDB

주어진 점 q를 기준으로 거리가 e 이하인 범위 내의 모든 점을 찾는 방법이다.

1) RER(Range Euclidean Restriction)

a. 알고리즘

1. 결과 집합 𝑅 ← ∅로 초기화
2. R-tree 등 공간 인덱스로부터 query인 q에서 유클리드 반경 e 안에 들어오는 모든 객체를 찾아서 집합화 한다. = S’
3. q와 연결된 점을 찾아서 edge segment를 만들고 <점,네트워크 거리>로 만든 뒤에 네트워크 거리 오름차순으로 정렬하는 큐(Q)에 넣는다.
4. Q에서 가장 네트워크 거리가 작은 원소(n) 하나를 꺼냈는데 n의 네트워크 거리가 e 보다 작고 S’가 비어있지 않다면
   • n과 인접한 한번도 방문하지 않은 점 n’를 찾아서 S’에서 원소 하나(s)를 꺼내어 nx에서 S까지 거리를 체크하고 e보다 작다면 result에 포함한 뒤 s는 S’에서 제거한다.
   • nx와 nx의 네트워크 거리를 Q에 넣는다.
5. result를 반환한다.

2) RNE(Range Network Expansion)

a. 알고리즘

1. 쿼리점 q와 네트워크 반경 e가 주어진다.
2. 네트워크 탐색을 통해 거리 e 이내에 닿는 모든 세그먼트들을 찾아 집합 QS로 만든다. QS는 쉽게 생각해서 간선들의 집합이라고 보면 된다.
3. 이제 QS에 포함된 세그먼트들 위에 있는 실제 데이터 객체들을 object R-tree를 이용해 검색한다:
   • R-tree의 각 노드 엔트리에 대해, 그 엔트리의 MBR이 QS의 어떤 세그먼트들과 연관되는지(교차하는지)를 계산해서(QS_i), QS_i가 비어 있지 않으면 그 자식 노드만 재귀적으로 탐색한다.
   • 리프 노드에서는 plane-sweep이나 유사한 방식으로 리프 내부 엔트리(객체 MBR)와 QS_i를 검사하여 실제 객체를 수집한다.
4. 중복된 객체가 있을 수 있으므로 정렬/중복 제거 후 최종 결과를 반환한다.

5. Closet-Pairs Euclidean Restriction

1) 알고리즘

입력: S(R-tree), T(R-tree), k(개수) 출력: 네트워크 거리 기준으로 가까운 k 쌍

1. 먼저 유클리드 기준으로 가장 가까운 k개 쌍을 구한다(즉 평면에서의 k-nearest pairs).
2. 각 초기 k쌍에 대해 네트워크 거리(도로상의 최단경로 거리)를 계산한다.
3. 네트워크 거리 기준으로 오름차순 정렬(가장 작은 거리부터).
4. 현재 top-k 중 가장 큰(=k번째) 네트워크 거리를 dEmax 로 설정(이 값이 갱신 임계값).
5. 아래 내용을 반복한다.
   • 다음으로 유클리드 기준에서 가까운 쌍을 하나 더 가져온다(스트리밍 방식으로 다음 유클리드 쌍을 반환).
   • 이 쌍의 네트워크 거리를 계산.
   • 새로 들어온 쌍이 현재 k번째보다 더 작으면(top-k 갱신 가능) 집어넣고 dEmax 재설정(항상 k번째의 네트워크 거리를 반영).
   • 종료조건: 다음으로 반환되는 유클리드 거리(d_E(s’,t’))가 현재 dEmax 보다 커지면 더 이상 네트워크 거리로 top-k를 교체할 수 없다. 따라서 반복을 종료한다.

참고자료

• Shashi Shekhar and Sanjay Chawla, Spatial Databases: A Tour, Prentice Hall, 2003
• P. RIigaux, M. Scholl, and A. Voisard, SPATIAL DATABASES With Application to GIS, Morgan Kaufmann Publishers, 2002