공간 데이터 베이스 - Spatial join

Posted Nov 5, 2025 Updated Nov 6, 2025

By Blake Woo 12 min read

Spatial join

1. 개요

두 공간이 겹치는 것을 어떻게 판별할 수 있을까? 이번에 포스팅할 내용은 점 혹은 객체가 서로 다른 R 트리나 서로 다른 Hash 기반 index에 있을 때
관계를 확인하는 방법에 대한 내용이다. 해당 관계가 교차인지 포함인지 근접인지는 실질적으로 체크를 해봐야하나 일단 이번 포스팅에서는 교차 기반으로 설명하겠다.

2. spatial R-tree join

1) Naive Join

두 R-트리를 동시에 재귀적으로 내려가면서, 각 노드(또는 엔트리)의 MBR(최소경계사각형)이 교차하는 경우만 더 세부적으로 검사하는 방식이다. 각 엔트리의 교차상태를 확인하고 교차한다면 엔트리가 MBR인지 Object인지 확인한 뒤에 Object라면 결과 셋에 추가하고 MBR이라면 안에 있는 Object들과 하나씩 비교하는 것이다. 당연하지만 각 TREE의 모든 값과 확인해야하므로 각 트리의 NODE 개수끼리 곱한 만큼 탐색을 해야한다.

비교 수 : R 트리 A의 LEAF 엔트리 개수 X R 트리 B의 LEAF 엔트리 개수

대략적인 수도코드로 나타내면 아래와 같다.

Join(R,S)
  Repeat
    Find a pair of intersecting entries E in R and F in S
    If R and S are leaf pages then 
      add (E,F) to result-set
    Else  Join(E,F)
  Until all pairs are examined

이 방법은 사실 쓸데없는 연산이 많다.
이것 말고 다른 좋은 방법으로는 아래와 같이 두 가지 방법이 있다.

2) Restricting the search space

먼저 검색 공간을 줄이는 방법이다. 아래의 알고리즘에 따라 비교하면 된다.

Join(R,S)
  Repeat
    Find a pair of intersecting entries E in R and F in S that overlap with IV
    If R and S are leaf pages then 
      add (E,F) to result-set
    Else  Join(E,F,CommonEF)
  Until all pairs are examined

자세히 설명하자면

R과 S, 2개의 R-Tree의 엔트리가 각각 서로 다른 R 트리의 범위와 겹치는지 확인한다.
겹치는 엔트리들 끼리만 다시 계산한다.

R-tree A와 B라고 할때 비교 수는 아래와 같다.

비교 수 : SIZE(A) + SIZE(B) + (SIZE(A에서 B와 겹치는 Entry 수) x SIZE(B에서 A와 겹치는 Entry 수))

3) Spatial sorting and plane sweep

한 개의 축을 따라 쭉 탐색하면서 체크하는 방식이다.
이는 설명하기 어려우므로 예시를 들어서 설명하겠다.

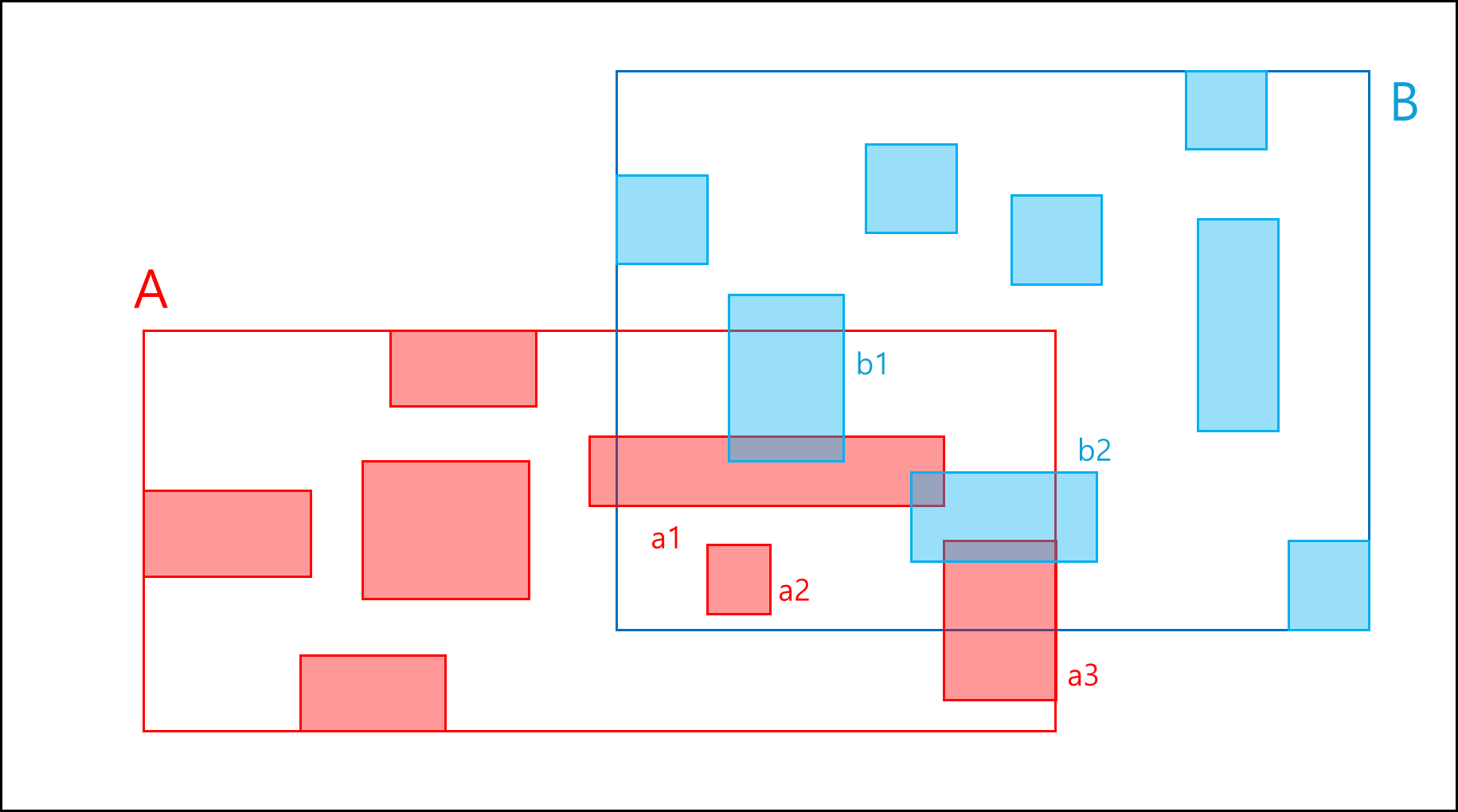
위와 같은 데이터가 있다고 해보자. A와 B는 각각 R-tree로 이루어진 공간 인덱스이며 각각 네모는 해당 R 트리가 포함하고 있는 MBR이다.

A와 B가 겹친 영역에 있는 MBR만 모두 가져온 뒤 MBR의 왼쪽 아래 점을 x축 기준으로 sort해서 하나씩 비교한다.
MBR 왼쪽 아래 점들을 기준으로 SORT하면 아래와 같다.

a1, a2, b1, b2, a3

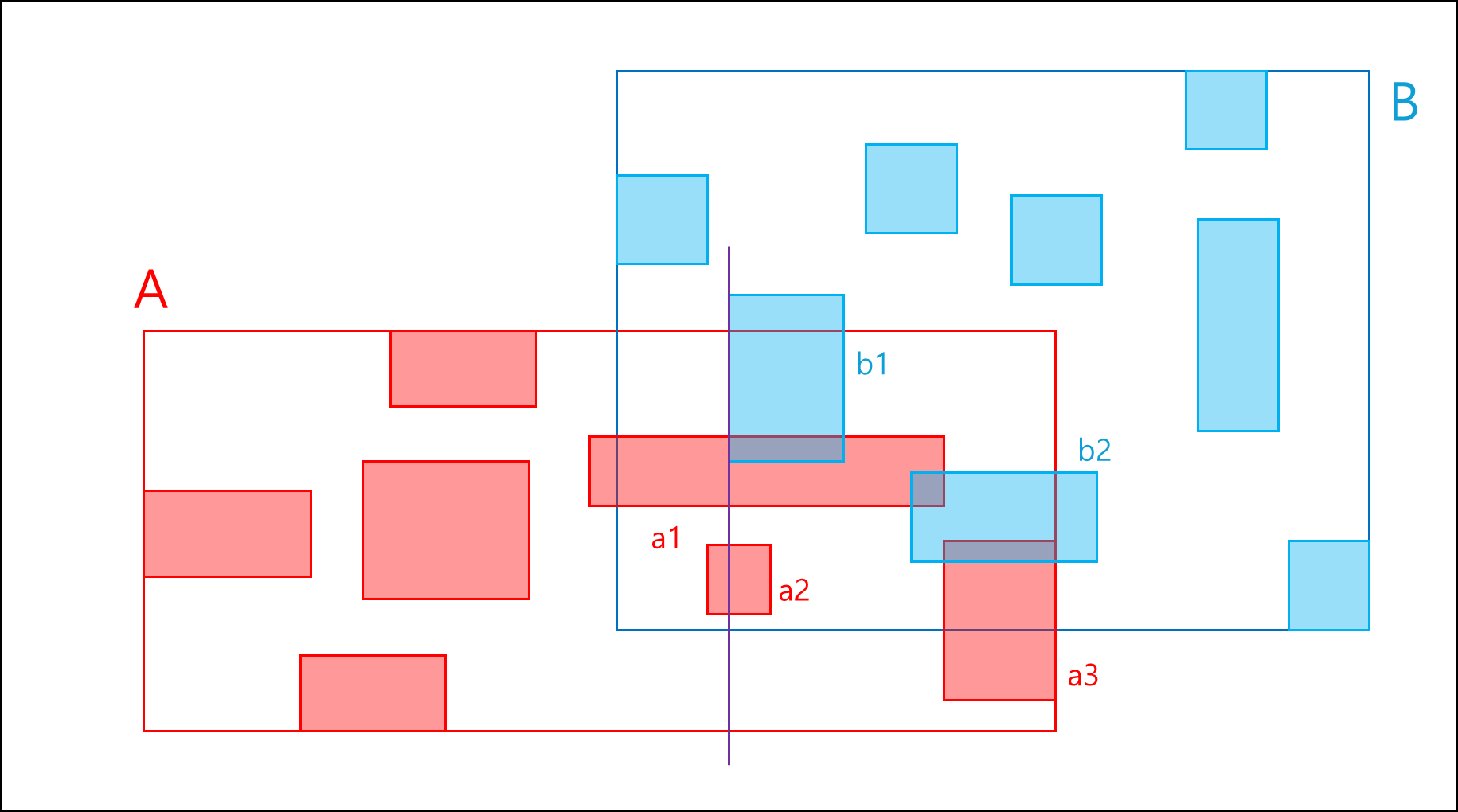
a1부터 x축 기준 겹치는게 있는지 체크해보는데 먼저 b1이 겹치는 것을 알수 있다.

b1이 겹치면 y축도 a1과 b1이 겹치는지 확인한다. 겹치는게 확인되면 result set에 (a1,b1)을 포함한다. 계속 탐색하다보면 b1과도 겹치는 것을 알 수 있다.

역시 y축으로도 겹치는지 확인하고 result set에 (a1,b2)를 포함한다.
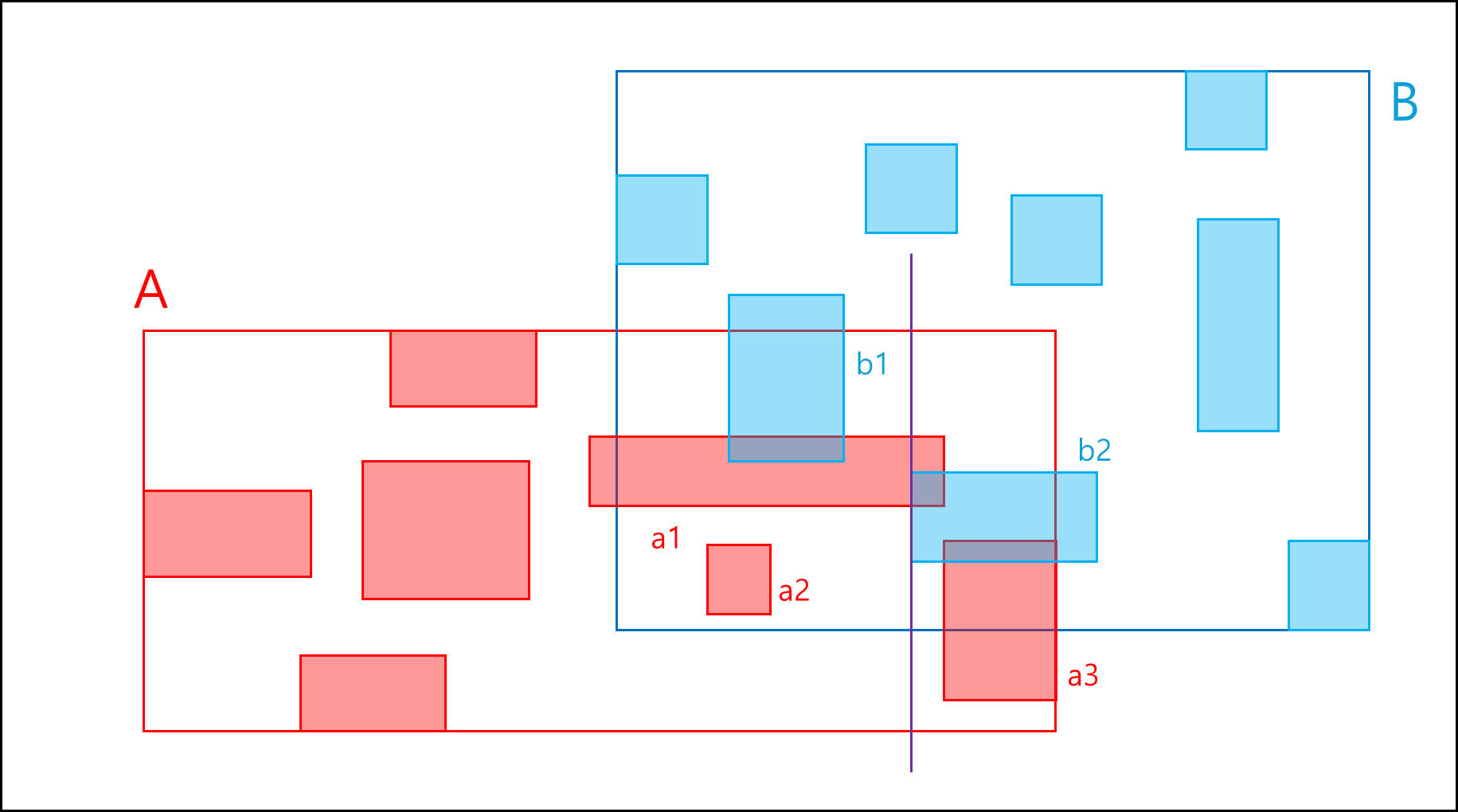
a1이 탐색이 끝나면 sort한 배열대로 그 다음은 a2를 따라 search하는데 b1과 x축은 겹치지만 y축은 겹치지 않으므로 넘어간다.

이런식으로 sort한 배열 원소를 하나씩 꺼내어 해당 MBR을 기준으로 x축을 따라가면서 비교하면된다.

위 예시의 총 비교량은 a1(2번) + a2(1번) + b1(1번) + b2(1번) + a3(0번) = 총 4번이다.

3. Spatial hash join

공간적 Hash join은 아래의 두 종류로 나뉜다.

1) Hash join based on Space-driven structures (with redundancy)

이 방식의 경우에는 간단한데, fixed grid나 grid file 같은 경우 이미 공간이 나누어져있으며 나누어진 어떤 해당 공간에 어떤 오브젝트가 점유하고 있는것을 확인하여 각 인덱스에서 동일한 단위 공간이 어떤 오브젝트에 의해 점유되고 있는것을 확인 후 세부적인 Join을 진행하면 된다.

2) Hash join based on Data-driven structures (with overlapping)

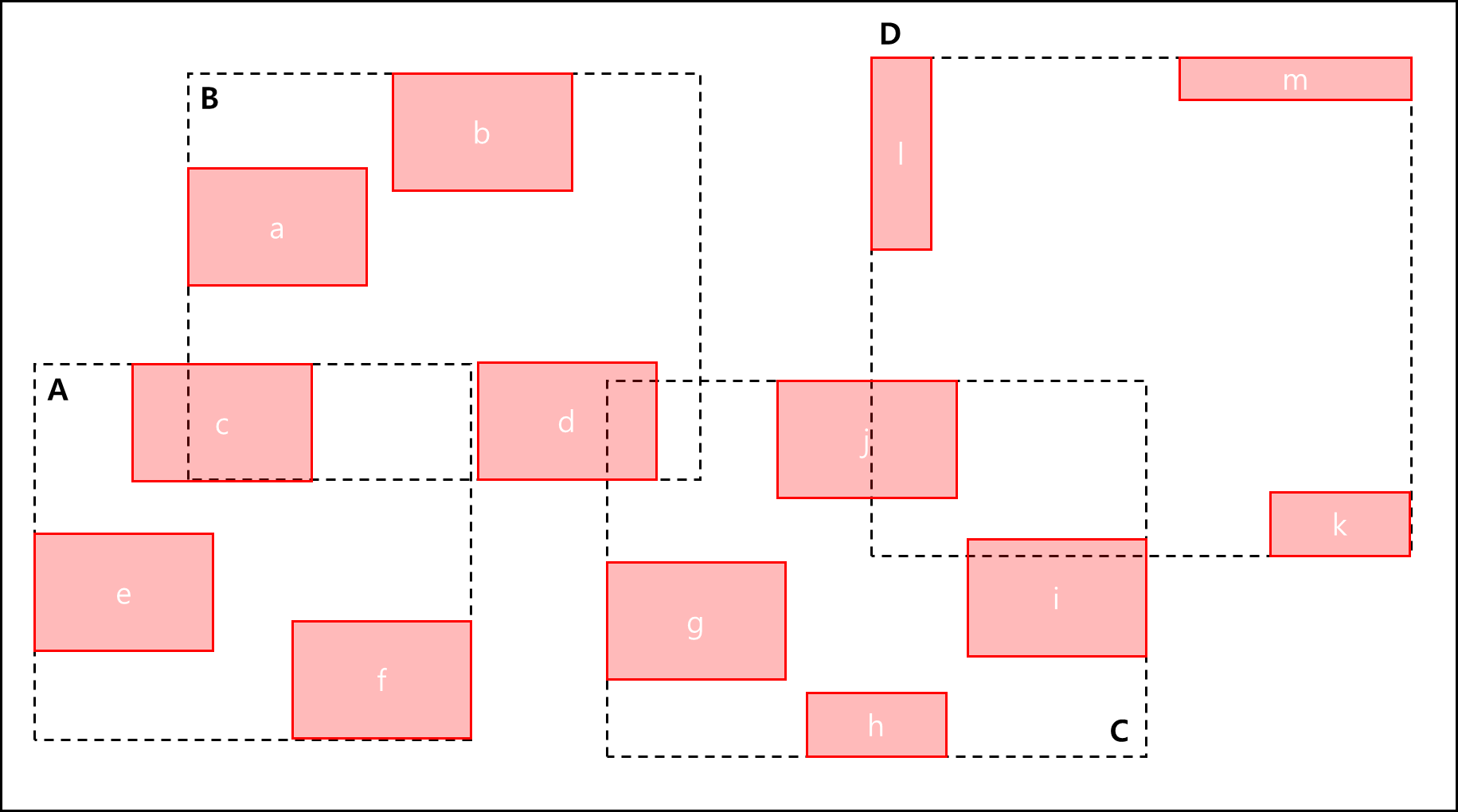
아래와 같은 R-tree가 있다고 해보자.

여기서 각각 MBR A~D까지만 떼다가 다른 R 트리와 겹치는 엔트리를 확인해본다.

다른 R 트리에서 1,2는 A’ 4,5는 B’ 3,7은 C’ 6,8은 D’라고 할 때 각각 A는 A’와 B는 B’와 C는 C’와 D는 D’와 JOIN 해볼 필요가 있으며 join시 Plane sweep같은 방법으로 축을 따라가면서 하나씩 확인해보는면 된다.

4. Z-ordering spatial join

Z-ordering으로 구성된 두 개의 index간의 교차하는 객체가 있는지 확인하는 방법이다.
서로 다른 z-ordering index R과 S를 키쌍 [z,oid]로 이루어진 L1과 L2로 만든다. 이 두 리스트(L1, L2)를 z-order로 병합(merge)하면서 접두사 관계(prefix)에 의해 후보 쌍을 추출하고 중복 제거 후 정밀 검사하는 방식이다.

만약 키 z가 z’의 접두사면 셀 z는 z’ 안에 있다고 해석할 수 있다.
가령 10이면 101이 10에 포함될 수 있다고 볼 수 있는데, 그려보기만해도 이건 맞는 말임을 알 수 있을 것이다.

L1과 L2의 원소 하나씩을 병합하면서 다른 키하나가 어떤 키의 접두사인 경우 해당 쌍을 후보로 모아두고 나중에 정밀 검사로 걸러내는 것이다. 그냥 말로 들으면 이해가 어려울테니 아래의 예시를 보자.

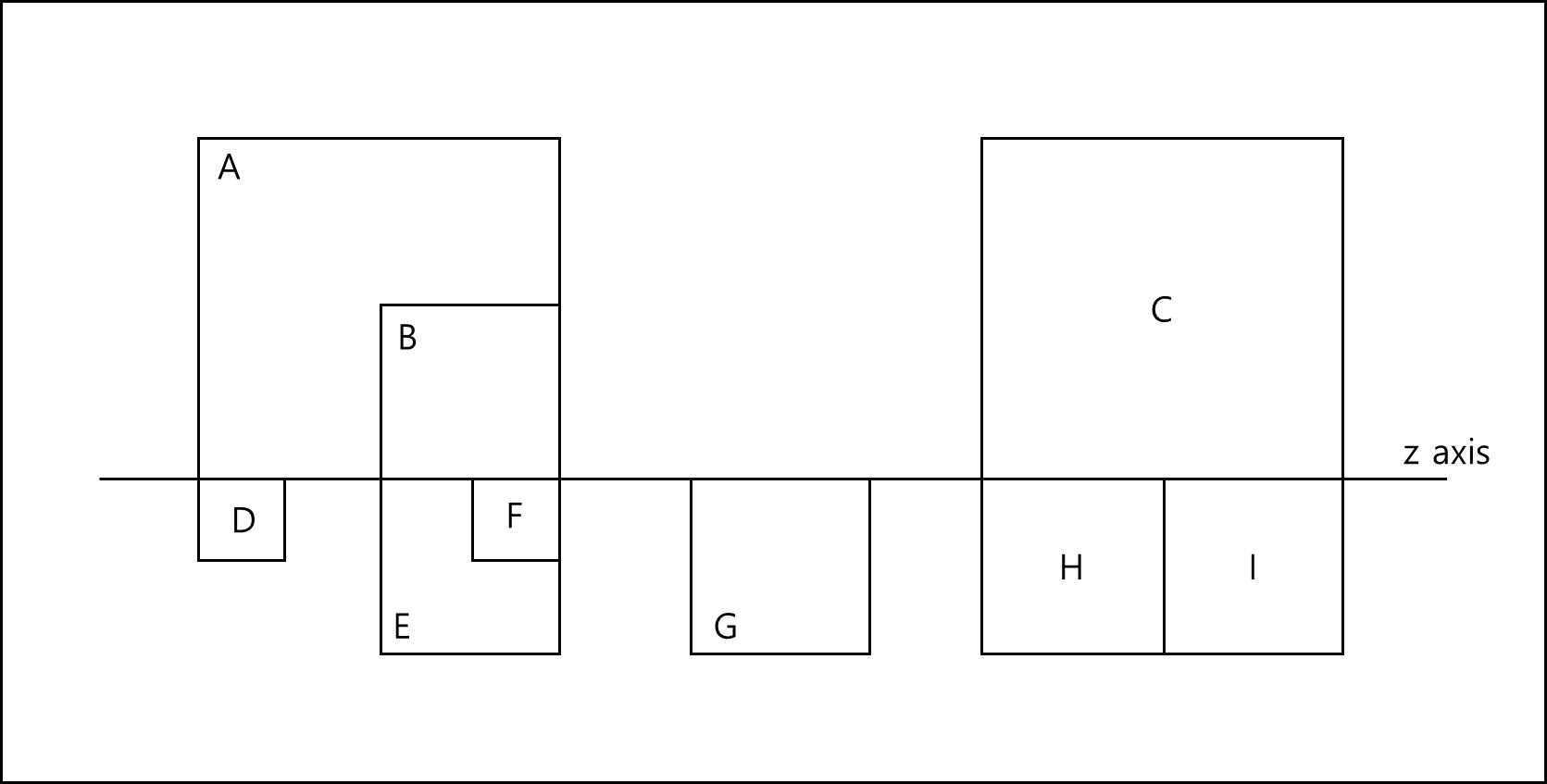
Index를 풀어서 선형으로 표현한 것을 축 하나를 두고 겹쳐둔 모양이다. z axis 위쪽은 L1 아래쪽을 L2라고 할 때 알고리즘은 아래와 같다.

준비 : 𝐿1 , 𝐿2를 각각 z 순서(증가)로 이미 정렬되어 있다.
병합 스캔: 두 리스트를 병합(merge) 방식으로 순회. 이때 리스트의 현재 위치들을 기준으로 스택(또는 컨텍스트) 을 유지한다.
이벤트와 scc 연산: 현재 리스트 항목들(top)에 대해 scc(…) 같은 연산(슬라이드에선 scc(top(S)) = …로 표기됨)을 통해 “현재 최하위/최소 포함 셀(smallest cell in the lower-right corner)”을 계산하고, 접두사 관계가 성립하면 후보 쌍을 즉시 결과 집합에 추가한다.
중복 제거: 동일 후보쌍이 여러 번 생성될 수 있으므로 후보들을 정렬해 중복을 제거한 뒤 refinement(정확한 기하 교차 검사) 수행.

아래 표는 위 예시를 실제로 Step by step으로 시행한 표이다. C1과 C2는 현재 읽은 항목 혹은 향후 읽을 항목의 컨텍스트고 S1과 S2는 각 리스트에서 현재 스텍에 쌓여있는 셀들이다. RESULT는 후보로 수집된 쌍을 말한다.

	C1	S1	C2	S2	Event Action
Step 0	A	()	D	()	event = current (L1) = A
Step 1	B	(A)	D	()	event = current (L2) = D
Step 2	B	(A)	E	(D)	event = scc(top(S2)) = D
Step 3	B	(A)	E	()	event = scc(top(S2)) = D, result={[A,D]}
Step 4	C	(B,A)	E	()	event = current (L1) = B
Step 5	C	(B,A)	F	(E)	event = current (L2) = F
Step 6	C	(B,A)	G	(F,E)	event = scc(top(S )) = B
Step 7	C	(A)	G	(F,E)	event = scc(top(S )) = B, result= {[A,D]} + {[B,F], [B,E]}
Step 8	C	()	G	(F,E)	event = scc(top(S )) = A, result= {[A,D],[B,F], [B,E]} + {[A,F],[A,E]}
Step 9	C	()	G	(E)	event = scc(top(S2)) = F, result= {[A,D],[B,F], [B,E], [A,F],[A,E]
Step 10	C	()	G	()	event = scc(top(S2)) = E, result= {[A,D],[B,F], [B,E], [A,F],[A,E]}
Step 11	C	()	H	(G)	event = current(L2) = G
Step 12	C	()	H	()	event = scc(top(S2)) = G, result= {[A,D],[B,F], [B,E], [A,F],[A,E]}
Step 13	eof(L1)	(C)	H	()	event = current(L1) = C
Step 14	eof(L1)	(C)	I	(H)	event = current(L2) = H
Step 15	eof(L1)	(C)	I	()	event = scc(top(S2)) = H, result= {[A,D],[B,F], [B,E], [A,F],[A,E]}+ {[H,C]}
Step 16	eof(L1)	(C)	eof(L2)	(I)	event = scc(top(S1)) = C, result= {[A,D],[B,F], [B,E], [A,F],[A,E],[H,C]}+ {[C,I]}
Step 17	eof(L1)	()	eof(L2)	()	event = scc(top(S2)) = I, result= {[A,D],[B,F], [B,E], [A,F],[A,E],[H,C],[C,I]} +{}

※ 추가 업데이트 및 검증 예정이다.

참고자료

Shashi Shekhar and Sanjay Chawla, Spatial Databases: A Tour, Prentice Hall, 2003
P. RIigaux, M. Scholl, and A. Voisard, SPATIAL DATABASES With Application to GIS, Morgan Kaufmann Publishers, 2002

Database

This post is licensed under CC BY 4.0 by the author.