공간 데이터 베이스 - Spatial keyword queries

Spatial keyword queries

1. 개요

이전까지의 포스팅은 단순히 공간 혹은 길에 대해서 거리만을 고려하여 검색했다면, 이번 포스팅은 지리적 위치와 텍스트 정보를 결합한 Geo-Textual 데이터를 질의하는 법에 대한 내용이다.

여기서 말하는 텍스트 정보는 크게 두 가지로 나뉜다.

• 정적 데이터
  위치를 포함한 웹페이지, 비즈니스 데이터와 같은 것

• 스트리밍 데이터
  트위터의 위치 태그, 체크인 정보와 같은 것
  일반적으로 텍스트, 위치, 시간으로 이루어져있다.

2. 표준 공간 키워드 Query

1) Boolean range query

질의 영역과 키워드 집합이 주어지면, 해당 영역 내에서 키워드를 포함하는 모든 객체를 반환한다.
해당 키워드를 모두 포함해야 대상에 속하며 하나라도 빠지면 대상에서 제외한다.

2) Top-k kNN query

유사도를 기준으로 가장 유사한 것 중 Top-K를 뽑아서 반환한다.
여기서 말하는 유사도는 아래의 공식을 따른다.

Objects: p=<λ,Ψ> (location, text)
Query: q=<λ,Ψ,k> (location, keyword, number of objects)

\[rank_{p}(p) = \alpha \frac{\left\| q.\lambda,p.\lambda \right\|}{maxD} + (1-\alpha)(1-\frac{tr_{q.\psi}(p.\psi)}{maxP})\]

여기서 $\alpha$는 $0 \le \alpha \le 1$ 이며 가중치이다.
위 수식을 보면 크게 두 부분으로 나눌 수 있다.
위치 정보에 따른 거리 $\left| q.\lambda,p.\lambda \right|$ 와 텍스트 적합성을 구하는 부분 $tr_{q.\psi}(p.\psi)$ 이다.

거리는 유클리드 거리를 구하는 방식으로 구하고 maxD를 나누는 정규화를 통해 0과 1사이의 값으로 변환한다. 이후 $\alpha$ 값을 곱해 거리에 대해서 얼마나 가중치를 줄 것인지 정한다.
텍스트 적합성 역시 maxP를 나누는 연산을 통해 정규화를 하여 0과 1사이의 값으로 변환한다. 하지만 $tr_{q.\psi}(p.\psi)$ 은 기본적으로 적합할 수록 크게 나오기 때문에 이를 적합 할 수록 작게 나오게 바꿔주기 위해 1에서 해당 값을 빼준다. 이 역시 $1-\alpha$ 값을 곱해줌으로써 가중치를 정해주는데 각각의 값이 $\alpha, 1-\alpha$ 값으로 곱해졌기 때문에 최대 1을 넘지 않는다.

3. 단일 객체 이상의 Query

1) co-location based ranking

어떤 키워드 관련 Object가 집적되어있는 곳을 찾는 방법이다.
서울로 치자면 용산이나 동대문과 같이 어떤 항목에 대해서 밀집된 곳이 있을 수 있는데, 이를 찾는 Query 처리 방법인것이다.

2) m-Closest Keywords (mCK) Query

m개의 키워드를 모두 커버하는 객체 그룹을 찾되, 그룹 내 객체들 간의 거리(diameter)를 최소화한다. 이 문제는 NP-hard이며, 정확한 해법과 근사 알고리즘이 존재한다. 주요 응용 분야는 태그를 통해 웹 리소스의 지리적 위치를 탐지하는 것이다

3) Collective Spatial Keyword Query

공간적 측면을 활용해 데이터 객체를 집계하고 집합적으로 질의를 만족하는 객체 그룹을 반환한다. 비용 함수를 이용하여 어떤 그룹을 반환할지 정하는데 비용 함수 결과 값이 작을 수록 더 적합한 그룹이다. 비용 합수는 아래와 같다.

Objects: p=<λ,Ψ> (location, text)
Query: q=<λ,Ψ> (location, keyword)

\[Cost(Q,\chi) = \alpha C_{1}(Q,\chi) + (1-\alpha)C_{2}(\chi)\]

$C_{1}$과 $C_{2}$는 아래와 같다.

\[C_{1}(Q,\chi) = \sum_{o\in\chi}Dist(o,Q)\] \[C_{2}(Q,\chi) = max_{o\in\chi}Dist(o,Q)+max_{o_{i},o_{j}\in\chi}Dist(o_{i},o_{j})\]

간단히 말하자면 $C_{1}$는 객체와 Query 간의 거리이며 $C_{2}$ 는 Object 값의 거리이다. 이 값 역시 가중치 $\alpha$ 로 어느쪽에 좀 더 비중을 둘 건지 정할 수 있다.

4) Top-k Groups Query

여러 객체 그룹을 랭킹하여 상위 k개 그룹을 반환하며, 거리, 직경(diameter), 텍스트 관련성을 모두 고려하게 되는데 해당 식은 아래와 같다.

Objects: p=<λ,Ψ> (location, text)
Query: q=<λ,Ψ,k> (location, keyword, number of objects)

\[rank_{q}(G) = \alpha \frac{\beta dist(q.\lambda,G)+(1-\beta) diam(G)}{maxD} + (1-\alpha)TR_{G}(q,\psi,G)\]

위 식에서는 가중치가 두 개가 등장한다. $\alpha$ 와 $\beta$ 인데, 둘다 0이상 1이하의 값이다.
$\beta$ 는 query에서 그룹까지의 거리와 그룹의 직경간에 어느쪽에 더 비중을 둘 것인지에 대한 가중치이고 $\alpha$ 는 키워드 적합도와 거리의 가까움에 대해 어떻게 비중을 둘 것인지에 대한 가중치이다.

4. 그외 기타 Query

1) Continuous Top-k Query

질의 위치가 연속적으로 변하는 상황에서 효율적 처리를 위해 safe zone 개념을 사용한다. 사용자가 해당 영역 내에 있으면 결과가 변하지 않는다

2) Reverse Spatial-Keyword kNN Query

새로운 상점을 추가할 때 어떤 상점들이 영향을 받을지 파악하거나, 소셜 미디어 광고의 최적 위치와 텍스트 내용을 찾아 최대 사용자에게 노출시키는 데 활용된다.

3) Why Not Spatial Keyword Top-k Queries

Top-k 결과에 특정 객체가 포함되지 않은 이유를 설명하고, k값 조정이나 키워드 수정 등의 개선 방법을 제안한다

4) Spatio-Textual Similarity Join

텍스트 유사도 임계값과 공간 거리 임계값을 만족하는 모든 객체 쌍을 검색한다.

5) Spatio-Textual Similarity Query

질의 영역, 키워드 집합, 텍스트 및 공간 유사도 임계값이 주어지며, 공간 유사도는 질의 영역과 결과 영역의 겹침(overlap)을 기반으로 측정된다

5. 텍스트 적합성(Text Representation)

Boolean range query에서 사용하는 텍스트 적합성은 기본적으로 Bag of Words를 변경한 IF-IDF 방식을 이용한다.
어떤 방식인지는 예를 들어 설명하겠다.

아래와 같은 Documents 3개가 있다. 각 Document 는 아래 단어의 집합이다.

D1 : apple, banana, chicken D2 : apple, cheese, chicken D3 : milk, cheese, ice

D1~D3 의 단어의 합집합을 만든다.

• apple, banana, chicken, cheese, milk, ice

이는 아래와 같이 표현한다. 각 단어에 대해서 Document에 포함된 숫자로 나타내고 없으면 0으로 표현하는 것이다.

	apple	banana	chicken	cheese	milk	ice
D1	1	1	1	0	0	0
D2	1	0	1	1	0	0
D3	0	0	0	1	1	1

위와 같이 변경하면 한 개의 Document는 자연수로 된 6차원의 벡터로 표현 가능하다.
하지만 0과 1로만 표현하면 어떤 값이 Document를 구분하는데 더 도움이 되는지 알수가 없으므로 TF-IDF(Term Frequency-Inverse Document Frequency)를 이용하여 각 값들을 가중치로 변경하게 된다.
해당 수식은 아래와 같다.

\[w_{j,i} = tf_{j,i} \times idf_{j}\]

여기서 $tf_{j,i}$는 document i에서 word j가 몇번 등장하는지이고 $idf_{j}$ 는 아래와 같은 식으로 구한다.

\[idf_{j} = log_{2}\frac{\left| D \right|}{\left| \left\{ document\in D | j\in document \right\} \right|}\]

분자인 $

D

$는 전체 document 총 개수이고 분모인

\[\left| \left\{ document\in D | j\in document \right\} \right|\]

는 word j가 있는 document의 개수이다.

“apple” 에 대해서 TF-IDF를 구해보자면 아래와 같다.

\[log_{2}\frac{\left| D \right|}{\left| \left\{ document\in D | j\in document \right\} \right|} = log_{2}\frac{3}{2} = 0.584\]

“milk”에 대해서 TF-IDF를 구해보자면 아래와 같다.

\[log_{2}\frac{\left| D \right|}{\left| \left\{ document\in D | j\in document \right\} \right|} = log_{2}\frac{3}{1} = 1.584\]

따라서 전체 표를 TF-IDF로 바꾸면 아래와 같다.

	apple	banana	chicken	cheese	milk	ice
D1	0.584	1.584	0.584	0	0	0
D2	0.584	0	0.584	0.584	0	0
D3	0	0	0	0.584	1.584	1.584

이렇게 변환한 벡터를 이용하여 COSINE 유사도를 이용하여 단어 적합성을 검사하면 된다.

※ Cosine 유사도

Cosine 유사도는 아래의 식을 따른다.

\[Cosine Similarity = \frac{(a\cdot b)}{\left\| a \right\| \times \left\| b \right\|}\]

여기서 $a\cdot b$ 은 벡터 a와 벡터 b의 내적이고 $\left| a \right|$ 는 a의 크기, $\left| b \right|$ 는 b의 크기이다.
만약 apple, milk, ice가 포함된 어떤 query Q와 D1의 TF-IDF 벡터의 코사인 유사도를 구하고 싶다면 아래와 같다.

Q = {0.584,0,0,0,1.584,1.584} D1 = {0.584,1.584,0.584,0,0,0}

\(Q \cdot D1 = 0.341056 + 0 + 0 + 0 + 0 + 0 + 0\)
\(\left\| Q \right\| \times \left\| D1 \right\| = 2.315 + 1.786 = 4.1\)
\(\frac{(a\cdot b)}{\left\| a \right\| \times \left\| b \right\|} = \frac{0.341056}{4.1} = 0.083\)

6. Indexing 방식

공간 정보와 keyword 정보를 같이 넣어서 Indexing을 미리해두면 빠르게 엑세스할 수 있다.
아래는 이러한 Indexing 방법들에 대한 설명이다.

1) R-IF (R-tree - Inverted File) Index

기존의 R-Tree 방식을 사용하되, R-tree의 Leaf-node에 포함된 Object 들에 Inverted File 형태로 keyword에 대한 정보를 포함하는 것이다.

해당 Indexing 방법은 Spatial한 query를 먼저 진행하여 거리 기반으로 객체를 갖고온 후 keyword를 확인하면 된다.
해당 Indexing 기법으로는 Boolean top-k나 Boolean Range query만 수행할 수 있다.

2) IF-R* (Inverted File - R*-tree) Index

R-IF는 R 트리에 IF를 달았다면 IF-R는 반대이다. Keyword에 대해 찾으면 그 keyword에 R-tree가 연결된 형태이다.

이 역시 Boolean top-k나 Boolean Range query만 수행할 수 있다.

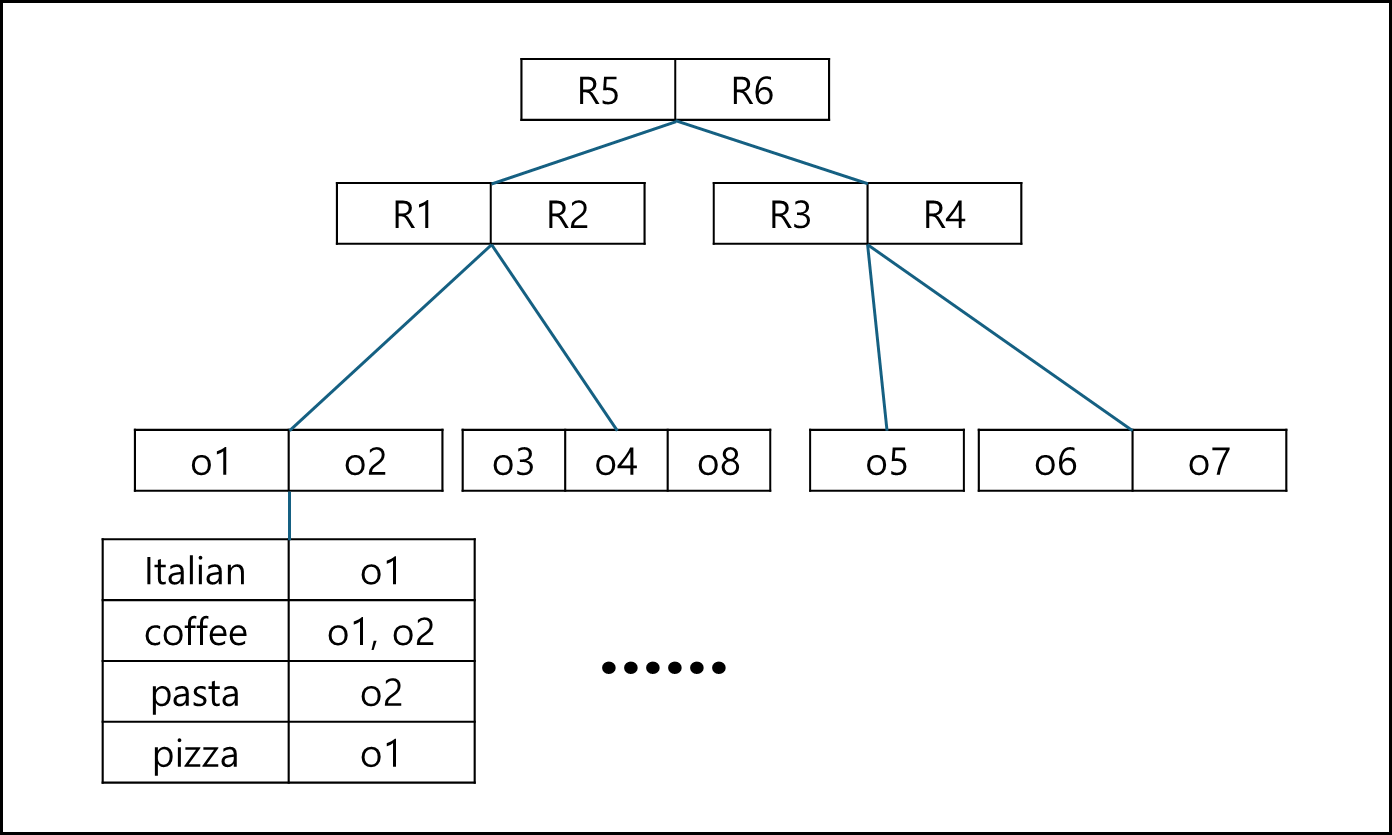
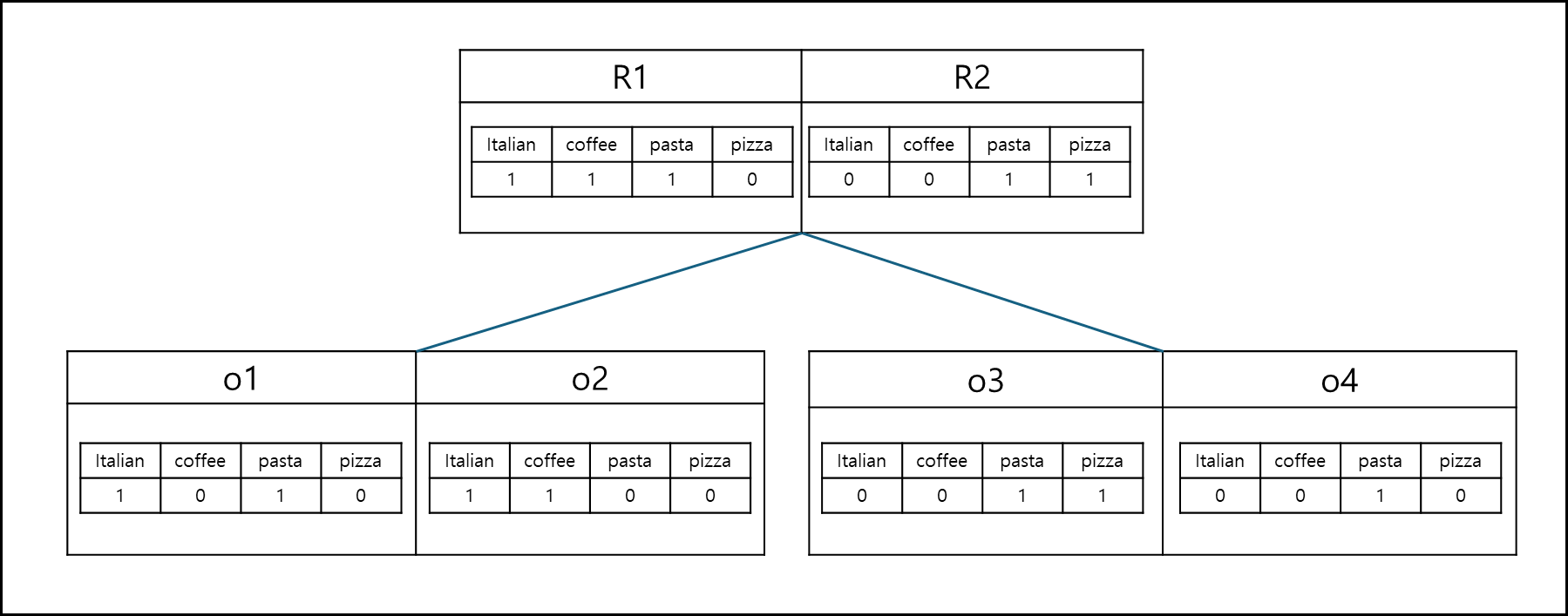
3) $IR^{2}$-Tree Index

Keyword에 대해서 Bitmap으로 표현한다. 단어는 한 개의 bit에 대응되며 있으면 1, 없으면 0으로 Mapping된다.
각 Object는 해당 bitmap을 갖고 있으며, Object를 child로 갖는 부모 노드는 각 object의 bitmap을 Logical OR한 값을 bitmap을 갖는다.

만약 어떤 keyword에 대해서 query를 요청하고자 하면 대상 keyword들에 해당하는 값들을 1로 세팅하여 각 node의 bitmap과 and하여 query 값과 동일한 값이 반환되는 node만 타고 내려가서 확인한다. 그 과정에서 확인 대상의 Node는 우선순위 큐에 넣고 하나씩 빼며 검색하며 사용하여 우선 순위 대상은 MBR일 경우 Mindist, Object의 경우 Dist이다.

이 Indexing 역시 Boolean top-k나 Boolean Range query만 수행할 수 있다.

4) IR-Tree Index

IR-Tree는 기본적으로 R 트리지만 모든 Node가 IVF를 갖고 있다. 이 IVF들은 기본적으로 어떤 단어를 어떤 Object가 몇개나 갖고 있는지에 대한 내용을 담고 있는데, 리프노드가 아니라 Inner node의 경우에는
하위 노드에서 가장 많은 빈도인 값만을 반영하여 두 개씩 모은다.

그와 별개로 Global하게 각 Object와 Inner node의 MBR에 대해서 Dist와 MINDIST를 구하여두고, 각 값에 대해서 $D_{ST}, MIND_{ST}$ 값 두 개를 구한다.
해당 값을 구하는 식은 아래와 같다.

\[D_{ST}(Q,O) = \alpha \frac{D_{\epsilon}(Q.loc,O.loc)}{maxD} + (1-\alpha)(1-\frac{P(Q.keywords|O.doc)}{maxP})\]

위 값은 앞부분은 Query와 대상 Object의 거리를 정규화한것이고, 뒤에는 Query의 키워드가 Object에 몇번이나 등장하는지를 산출하되
유사도는 클 수록 값이 높으므로 정규화한 값을 1에서 빼줌으로써 유사할 수록 작은 값이 반환되게 만들고 $\alpha$ 값으로 거리와 keyword의 비중을 정하는 방식이다.

\[MIND_{ST}(Q,N) = \alpha \frac{MIND_{\epsilon}(Q.loc,N.rectangle)}{maxD} + (1-\alpha)(1-\frac{P(Q.keywords|N.doc)}{maxP})\]

위 값은 Query와 MBR 간의 MINDIST 거리를 정규화하고, MBR에서 Query의 Keyword의 등장 빈도를 산출하되
유사도는 클 수록 값이 높으므로 정규화한 값을 1에서 빼줌으로써 유사할 수록 작은 값이 반환되게 만들고 $\alpha$ 값으로 거리와 keyword의 비중을 정하는 방식이다.

\[maxP=\prod_{t\in Q.keywords}max_{O'\in D} \hat{p}(t|O'.doc)\]

maxP값은 등장 빈도를 정규화할때 사용하는 값인데, 각 Object에서 가장 많이 등장하는 키워드의 확률을 모두 곱한 값이다.

\[\hat{p}(t|\theta _{O.doc}) = (1-\lambda)\frac{tf(t,O.doc)}{\left| O.doc \right|}+\lambda \frac{tf(t,Coll)}{\left| Coll \right|}\]

위 값은 기본적으로 키워드 t가 Object에 등장할 확률을 추정할때 사용하는 것으로 단어 t가 해당 Object에서 직접 등장할 확률에 단어 t가 전체 Object에서 등장할 전체 비율을 더하되 $\lambda$ 값으로 비중을 주는 것이다.

\[P(Q.keywords|N.doc) = \prod_{t\in Q.keywords}\hat{p}(t|\theta _{O.doc})\]

위 값은 객체 O의 문서에서 키워드 t가 나올 확률을 모두 곱한 것이다.

위 식들을 기반으로 kNN Search는 아래와 같은 알고리즘으로 구동된다.

1. K 후보큐 KQ 초기화(K개의 크기)
2. 우선 순위 큐(Q) 초기화
3. Q에 루트 노드 삽입
4. 큐가 비어있지 않다면 Q의 원소(E)를 하나 꺼내서 아래의 절차 수행
5. E가 Object일때 :
   • 아직 더 가까운 후보가 남아있고 꺼낸 객체가 Q에서 첫번째 후보보다 멀면($D_{ST}$ > Queue.First().key) E의 $D_{ST}$를 키로 다시 큐에 넣는다
   • 아니라면 E를 KQ에 넣고, KQ가 꽉 찼으면 알고리즘 종료
6. E가 Leaf node라면 :
   • E의 Object들의 $D_{ST}$를 키(Key)로 모두 Q에 삽입
7. E가 InnerNode라면 :
   • E의 Node들들의 $MIND_{ST}$를 키(Key)로 모두 Q에 삽입

※ 추가 업데이트 및 검증 예정

참고자료

• Shashi Shekhar and Sanjay Chawla, Spatial Databases: A Tour, Prentice Hall, 2003
• P. RIigaux, M. Scholl, and A. Voisard, SPATIAL DATABASES With Application to GIS, Morgan Kaufmann Publishers, 2002
• Cao et al. Retrieving Top-k Prestige-Based Relevant Spatial Web Objects. VLDB11.
• Zhang et al. Keyword search in spatial databases: Towards searching by document. ICDE 2009.
• Zhang et al. Locating mapped resources in web 2.0. ICDE 2010.
• Guo et al. Efficient algorithms for answering the m-closest keywords query. SIGMOD’15
• Cao et al. Efficient Processing of Spatial Group Keyword Queries. TODS’15
• Skovsgaard and Jensen. Finding top-k relevant groups of spatial web objects. VLDB J. ’15
• Lu et al. Reverse Spatial and Textual k Nearest Neighbor Search. SIGMOD, 2011
• Choudhury et al. Maximizing bichromatic reverse spatial and textual k-NN queries. VLDB’16
• Chen et al. Answering why-not questions on spatial keyword top-k queries. ICDE’15
• Chen et al. Answering why-not spatial keyword top-k queries via keyword adaption ICDE’16
• Bouros et al. Spatio-Textual Similarity Join, PVLDB‘12
• Fan et al.: SEAL: Spatio-Textual Similarity Search, PVLDB 12