그래프 2

그래프 연산

깊이 우선 탐색 (DFS - Depth First Search)

탐색을 시작하는 노드 v에서 인접하며 방문하지 않은 노드 w를 방문 w에서 인접하며 방문하지 않은 노드를 y를 방문 위 과정을 반복하여 탐색하면 깊이 우선 탐색이다. 재귀 함수를 통하거나 stack을 통해 구현 가능하다.

넓이 우선 탐색 (BFS - Breath First Search)

탐색을 시작하는 노드 v에서 인접하며 방문하지 않은 노드 모두를 방문 v에서 인접한 노드 중 첫번째 노드 w를 선택하여 w에 인접하며 방문하지 않은 노드 모두를 방문 위 과정을 반복하여 탐색하면 넓이 우선 탐색이며 queue를 이용하여 구현 가능하다.

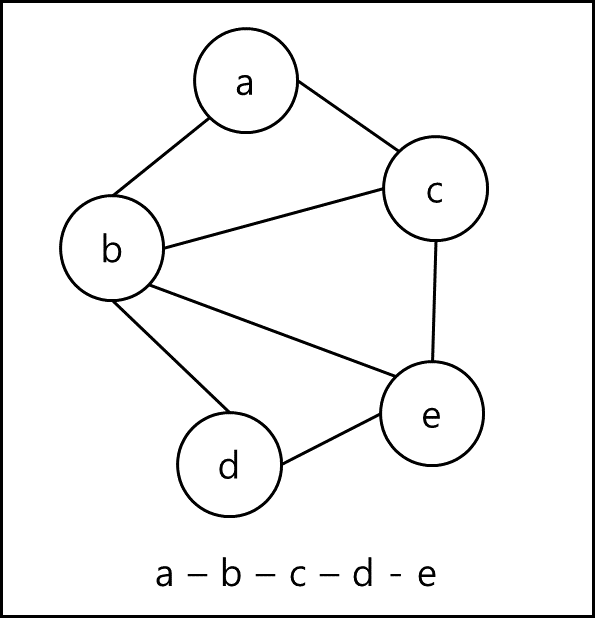
신장 트리(Spanning Tree)

그래프에 포함된 노드 전체를 포함하며 그래프에 포함된 간선으로 이루어져있되 트리이기 때문에 사이클이 없어야한다.

최소 비용 신장트리 (Minimum Cost Spanning Tree)

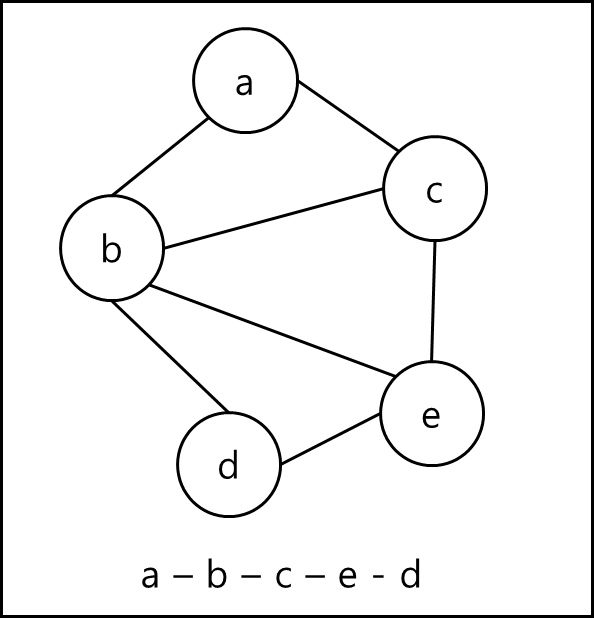
가중치가 부여된 무방향 그래프에서 신장 트리를 구성하는 edge들의 비용의 합이 가장 작은 경우 해당 트리는 최소 비용 신장 트리라고 부른다. 이러한 최소 비용 신창 트리를 구하는 것에는 여러 방법들이 있다. 이런 방법을 설명하기 위해 예시 그래프 T를 아래와 같이 정의하고 시작하겠다.

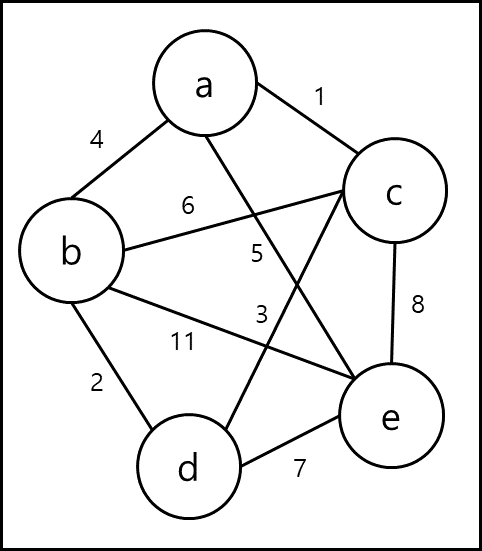
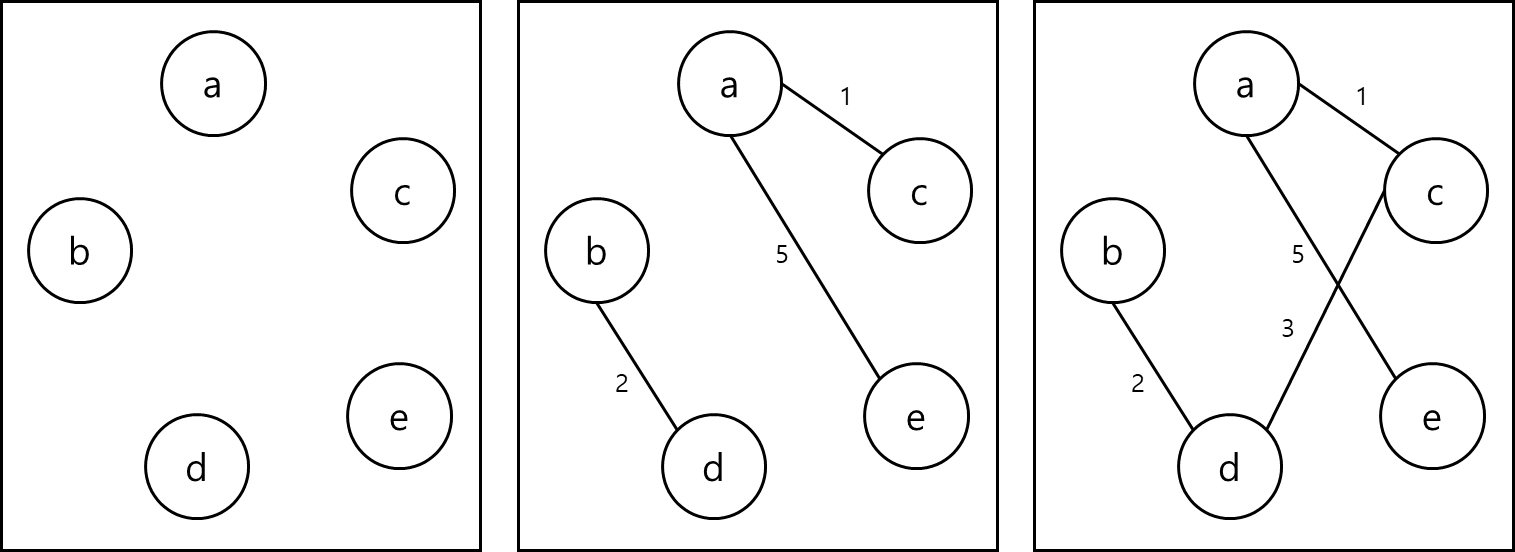
Kruskal algorithm

Edge들을 비용으로 오름차순 정렬한 뒤 가장 비용이 적은 edge부터 하나씩 선택한다 선택된 edge는 기존에 선택된 edge들과 사이클을 형성하지 않을 경우에만 최소비용 트리에 포함한다. 그래프 G의 모든 노드가 연결되어있고 N>0개의 노드가 있다면 정확히 N-1개의 Edge가 선택되게 된다.
정의해둔 그래프 T를 가지고 설명을 해보겠다.
처음에 그래프 T의 Edge들을 오름차순으로 정렬하면 1, 2, 3, 4, 5, 6, 7, 8, 11순으로 정렬된다. 가장 가중치가 적은 것부터 선정하면 1,2,3을 선택하게 되는데 이때 4를 선택하게되면 사이클이 생기므로 4는 선택하지 않는다.

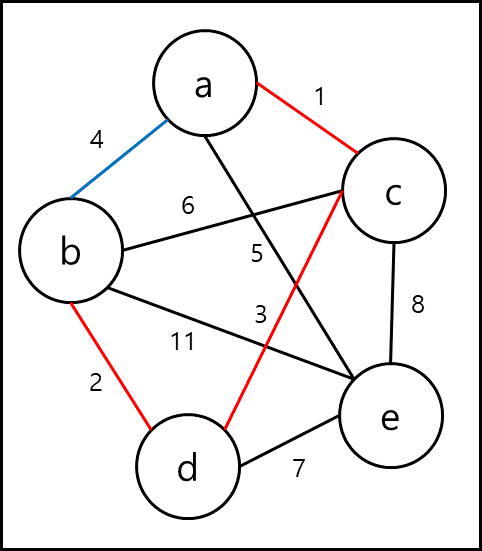
마지막으로 5를 선택하게 되면 선택한 edge가 노드 개수 -1 이되므로 최소 비용 신장트리가 완성된다.

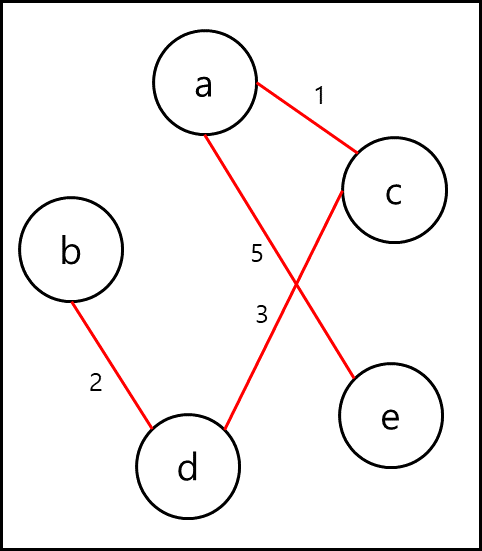
이때 가장 중요한 것은 해당 edge를 추가함으로써 사이클이 생기는지 생기지 않는지 검출 할 수 있는 방법인데 이때 자주 사용하는 방법은 union-find 이다. 이 union-find 방법도 설명은 매우 간단한데 해당 노드에 연결된 값을 기준으로 표를 작성하고 그 표를 기준으로 찾는 것이다. 아래와 같은 임의의 그래프 두개가 있다고 할때

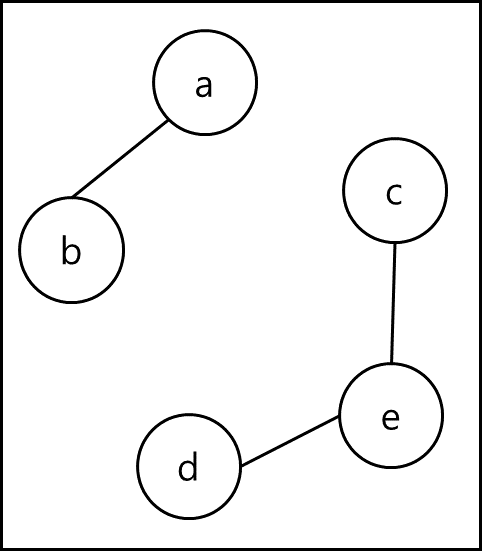
union 방법으로 표를 작성하면 아래와 같이 작성할 수 있다.

대상 노드	a	b	c	d	e
부모 노드	a	a	c	c	c

특정 노드에 연결된 간선을 타고 가장 작은 node의 값이 나올때까지 재귀적으로 탐색한 뒤 부모 노드의 값으로 기재해두는 것이다. 이렇게 만들어두면 특정 두 개의 node를 선택했을때 해당 node가 같은 그래프에 포함되어있는지 알 수 있다. node a와 node c를 비교해보겠다. a의 경우 부모노드는 본인인 a, c도 본인인 c이다. 그렇다면 연결이 되어있지 않다는 뜻이므로 두 노드간에 간선이 추가되어도 사이클이 생기지 않는다는 뜻이다. 하지만 node a와 node d로 대상을 바꿔보자. 표 상에서는 둘다 부모노드가 c이다. 이 말은 서로 연결되어있다는 뜻이고 두 노드간에 간선이 생긴다는 것은 사이클이 생기게 된다는 것을 뜻한다.

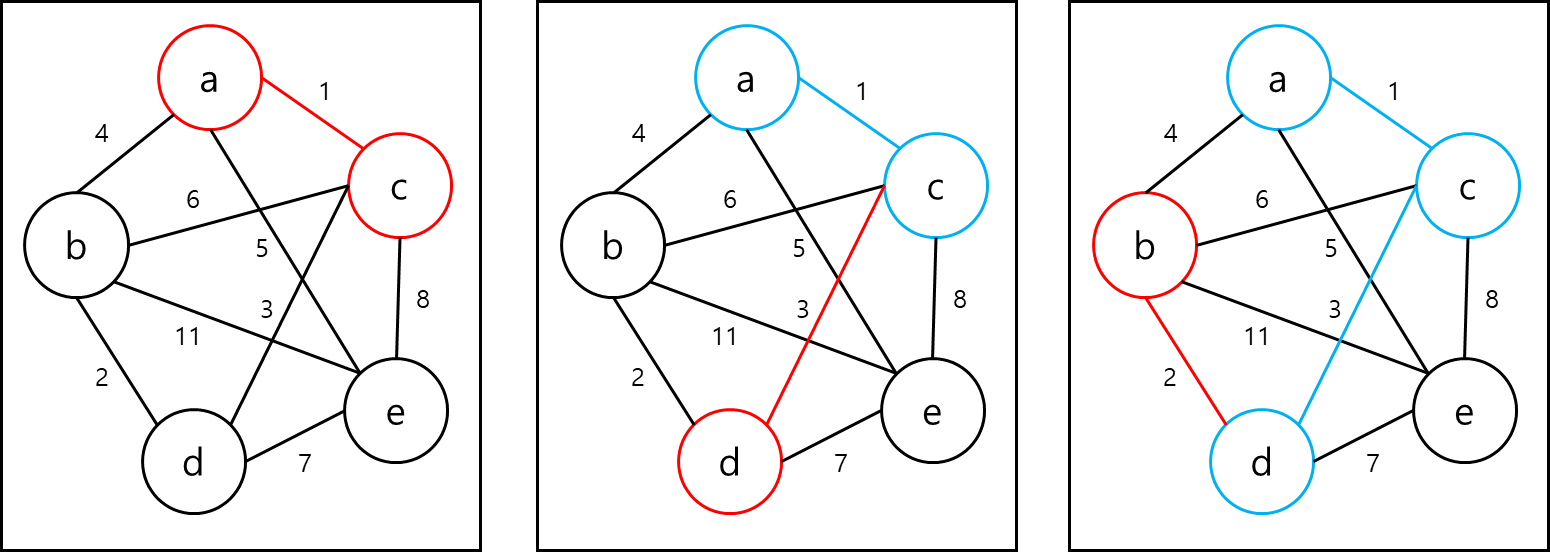
Prim algorithm

처음에 한 개의 노드를 선택하여 비어있는 트리 M에 넣는다 이후에 M안에 있는 노드 A와 M안에 없는 노드 B간의 edge중에 가중치가 가장 작은 것을 선택하여 edge를 포함시킨 뒤 노드 B를 M에 포함한다. 이후 계속해서 이런 방법으로 노드를 전부 추가하게되면 최소 비용 신장 트리가 나온다. 정의해둔 그래프 T를 예시로 그림으로 표현 해보겠다.

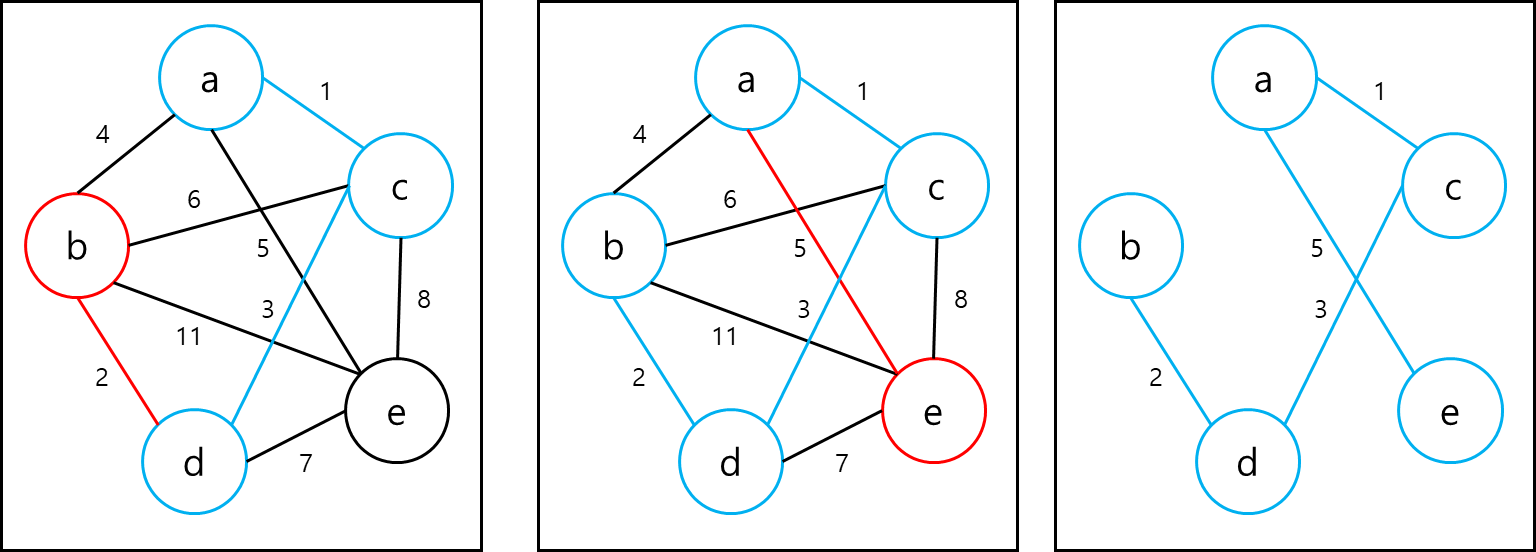
Sollin algorithm

솔린 알고리즘을 이해하기 위해서는 포레스트라는 개념이 필요한데, 이 포레스트는 서로 연결되지 않은 트리들의 집합이다. 초기에는 모든 각각의 node들이 tree로써(root 노드 하나인 트리) 포레스트에 포함되어있다. 한번에 한 개의 edge만 추가하는 쿠르스칼 알고리즘이나 프림 알고리즘과 달리 이 솔린 알고리즘은 포레스트 내의 모든 Tree들에서 최소 가중치 edge만을 취한다. 각 트리에서 중복된 edge를 선택하는 것만 처리해주면 문제없이 최소 비용 신장 트리가 완성된다. 정의해둔 그래프 T를 예시로 그림으로 표현 해보겠다.

참고 자료

• 학부생시절 자료구조 강의 자료
• 블로그스키