Post

기계학습 - K-means

Posted Updated
By Blake Woo 10 min read

K-means

1. 개요

데이터를 여러 그룹으로 나누는 분할법의 일종이다.
초기에 K개의 중심점을 선정하여 해당 중심점을 기준으로 각 점들과의 거리를 계산하여 가까운 중심점에 할당하여 K개의 클러스터를 만들어내는 식이다. 이 알고리즘은 자율 학습의 일종으로, 레이블이 달려 있지 않은 입력 데이터에 레이블을 달아주는 역할을 수행한다.

2. 절차

가장 최초의 K-means 방식의 절차를 아래와 같다.

(1) 각 점을 가장 가까운(유클리드) 중심(centroid)에 할당한다. (2) 각 클러스터의 점들로 평균(centroid)을 갱신하여 할당이 바뀌지 않으면 종료한다.

지금 사용하는 방식도 크게 다르지는 않지만 여기서 몇 가지 변경이 생기면서 종류가 생겼다.

※ 예시

1) 초기 설정

k가 2일때를 상정하여 예를 들어보이겠다. 아래는 임의로 선정한 2차원 데이터 6개이다. A = (1.0, 2.0) B = (1.5, 1.8) C = (5.0, 8.0) D = (8.0, 8.0) E = (1.0, 0.6) F = (9.0,11.0)

여기서 중심값이될 값 2(K)개를 무작위로 선정하겠다. 유 centroid₁ = A = (1.0, 2.0) centroid₂ = D = (8.0, 8.0)

2) 반복 1

각 점에서 두 중심까지의 거리를 계산한다. 유클리드 거리 로 계산하겠다.

  • A (1.0,2.0):
    d(A, centroid₁) = 0.000 (자기 자신)
    d(A, centroid₂) = 9.220
    → A → centroid₁

  • B (1.5,1.8):
    d(B, centroid₁) = 0.539
    d(B, centroid₂) = 8.983
    → B → centroid₁

  • C (5.0,8.0):
    d(C, centroid₁) = 7.211
    d(C, centroid₂) = 3.000
    → C → centroid₂

  • D (8.0,8.0):
    d(D, centroid₁) = 9.220
    d(D, centroid₂) = 0.000
    → D → centroid₂

  • E (1.0,0.6):
    d(E, centroid₁) = 1.400
    d(E, centroid₂) = 10.186
    → E → centroid₁

  • F (9.0,11.0):
    d(F, centroid₁) = 12.042
    d(F, centroid₂) = 3.162
    → F → centroid₂

첫 반복 결과는 아래와 같다.

  • Cluster 1 (centroid₁에 할당): {A, B, E}
  • Cluster 2 (centroid₂에 할당): {C, D, F}

이제 새 중심점을 찾는다.

  • Cluster1의 새 centroid₁’ = mean{A, B, E}
    x = (1.0 + 1.5 + 1.0) / 3 = 3.5 / 3 = 1.166666… (≈ 1.1667)
    y = (2.0 + 1.8 + 0.6) / 3 = 4.4 / 3 = 1.466666… (≈ 1.4667)
    → centroid₁’ = (1.1666667, 1.4666667)

  • Cluster2의 새 centroid₂’ = mean{C, D, F}
    x = (5.0 + 8.0 + 9.0) / 3 = 22 / 3 = 7.333333… (≈ 7.3333)
    y = (8.0 + 8.0 + 11.0) / 3 = 27 / 3 = 9.0
    → centroid₂’ = (7.3333333, 9.0)

2) 반복 2

새로 구한 중심점에 대해서 각 점에 대한 할당 변경이 바뀌었는지 확인한다.

  • A: d(A, centroid₁’) = 0.5588, d(A, centroid₂’) = 9.4399 → A → centroid₁’
  • B: d(B, centroid₁’) = 0.4714, d(B, centroid₂’) = 9.2665 → B → centroid₁’
  • C: d(C, centroid₁’) = 7.5749, d(C, centroid₂’) = 2.5386 → C → centroid₂’
  • D: d(D, centroid₁’) = 9.4540, d(D, centroid₂’) = 1.2019 → D → centroid₂’
  • E: d(E, centroid₁’) = 0.8825, d(E, centroid₂’) = 10.5200 → E → centroid₁’
  • F: d(F, centroid₁’) = 12.3388, d(F, centroid₂’) = 2.6034 → F → centroid₂’

할당 값이 변경되지 않았으므로 알고리즘이 종료된다.

3. 변수 선정 방법

1) 초기화 기법

눈치 챘겠지만 이 K-means 방식은 초기값에 매우 민감하다.
따라서 초기값을 제대로 선정하지 못하면 성능이 매우 떨어질 수 있다.

이 초기값을 잡는 법은 여러가지가 있다.

a. 무작위 선택

데이터에서 무작위로 k개의 관측값을 골라 처음 중심으로 삼는데 이후 각 클러스터에 배당된 점들의 평균 값을 초기 $\mu _{i}$로 설정한다 중심점이 결국에는 실제 군집의 중앙으로 수렴하는 특성을 지닌다.

b. Forgy

데이터에서 무작위로 k개의 관측값을 골라 처음 중심으로 삼는데, 이후 중앙값을 내서 조정하지 않고 그 값 자체를 중심점으로 삼는다.

c. MacQueen

데이터 집합으로부터 임의의 k개의 데이터를 선택하여 각 클러스터의 초기 $\mu _{i}$로 설정한다. 이후 선택되지 않은 각 데이터들에 대해, 해당 점으로부터 가장 가까운 클러스터를 찾아 데이터를 배당한다. 모든 데이터들이 클러스터에 배당되고 나면 각 클러스터의 무게중심을 다시 계산하여 초기 $\mu _{i}$로 다시 설정한다.

무작위 선택법과는 다르게 평균이 아니라 무게중심으로 선정하기 때문에 최종 수렴에 가까운 클러스터를 찾는 것은 비교적 빠르나, 최종 수렴에 해당하는 클러스터를 찾는 것은 매우 느리다

d. Kaufman

전체 데이터 집합 중 가장 중심에 위치한 데이터를 첫번째 $\mu _{i}$로 설정한다. 이후 선택되지 않은 각 데이터들에 대해, 가장 가까운 무게중심 보다 선택되지 않은 데이터 집합에 더 근접하게 위치한 데이터를 또 다른 $\mu _{i}$로 설정하는 것을 총 k개의 $\mu _{i}$가 설정될 때까지 반복한다.

e. k-means ++

  1. 데이터에서 임의의 한 점을 첫 번째 중심으로 균등 무작위 선택한다.
  2. 각 점 𝑥에 대해 거리를 계산하는데 현재까지 선택된 중심들 중 가장 가까운 중심과의 유클리드 거리(또는 거리의 제곱)로 계산한다.
  3. 다음 중심은 각 점 𝑥가 선택될 확률을 ∝ $D(x)^{2}$ 로 하여 샘플링한다
  4. 2–3을 반복해 총 k개의 중심을 선택한다.
  5. 그 다음부터는 표준 k-means(Lloyd)를 수행해 중심을 갱신·수렴시킨다.

요컨대 멀리 떨어진 점들이 높은 확률로 먼저 선택되므로 중심들이 고르게 퍼지게 된다.

2) K값 선정

a. Rule of thumb (경험 법칙)

데이터 수가 n이라 할때, 필요한 클러스터 수는 다음과 같이 계산할 수 있다.

\[k \approx \sqrt{\frac{n}{2}}\]

b. Elbow Method

군집 내 제곱합(WCSS) 감소율이 현저히 느려지는 지점을 찾아 적용하는 방식이다. 여기서 말하는 군집내 제곱합은 동일한 군집에 속한 모든 데이터 포인트에 대해서 해당 군집의 중심점과의 제곱 거리를 합산한 값으로 각 군집에 대해서 구한 뒤 모두 더하면 총 WCSS가 된다. K가 늘어남에 따라 총 WCSS를 구하면 아래와 같은 그래프가 된다.

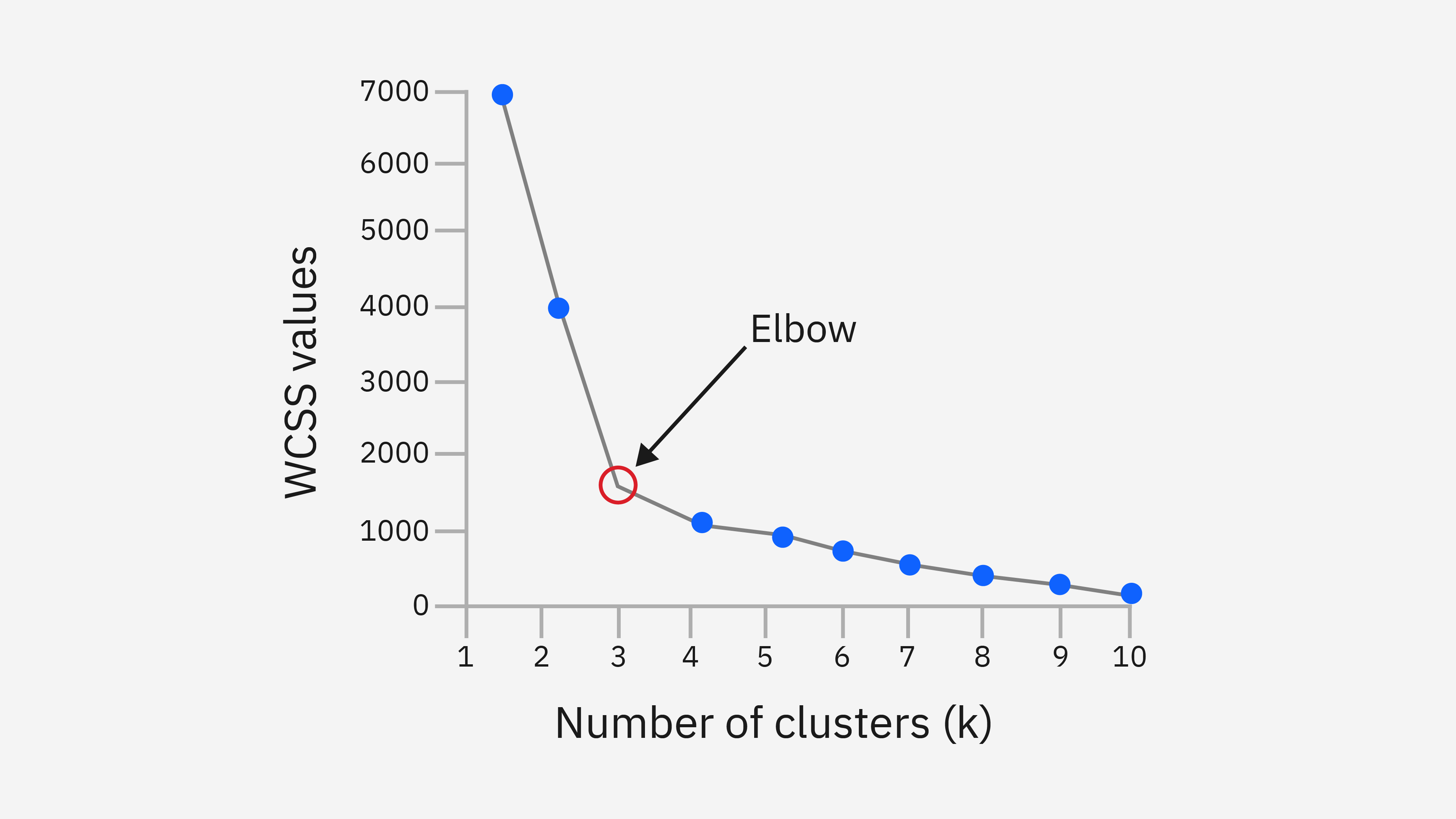
img.png
그림 출처 : https://www.ibm.com/think/topics/k-means-clustering

위의 그래프에 급격하게 총 WCSS가 떨어지는 지점이 꼭 팔꿈치 모양을 닮았다고 하여 Elbow Method이며 이 지점은 군집 수와 군집 내 분산 간의 최적의 균형을 나타낸다.

c. Information Criterion Approach

클러스터링 모델에 대해 가능도를 계산하는 것이 가능할 때 사용하는 방법으로, 베이지안 정보 기준 등이 있다. k-평균 클러스터링 모델의 경우 가우시안 혼합 모델에 가깝기 때문에, 가우시안 혼합 모델에 대한 가능도를 만들어 정보 기준 값을 설정할 수 있다.

참고 자료

  • 위키 백과 - K 평균 알고리즘
  • IBM - K-means clustering
  • Lloyd, S. P., Least Squares Quantization in PCM, IEEE Transactions on Information Theory, vol. 28, no. 2, pp. 129–37, from https://www.cs.nyu.edu/~roweis/csc2515-2006/readings/lloyd57.pdf, March 1, 1982. DOI: 10.1109/TIT.1982.1056489
  • McQueen, James B. “Some methods of classification and analysis of multivariate observations.” . In Proc. of 5th Berkeley Symposium on Math. Stat. and Prob. (pp. 281–297).1967.
  • Arthur, D. & Vassilvitskii, S., “k-means++: The Advantages of Careful Seeding” (2007).
Machine Learning
AI Machine Learning K-means
This post is licensed under CC BY 4.0 by the author.