데이터 베이스 - LSM Tree(Log-structured merge-tree)
LSM Tree(Log-structured merge-tree)
1. 개요
먼저 LSM Tree(Log-Structured Merge-Tree)를 한 마디로 표현하자면 데이터베이스 시스템에서 고속 쓰기(high insert volume) 워크로드를 효율적으로 처리하기 위해 설계된 디스크 기반 데이터 구조이다.
데이터 베이스의 구조로 그냥 B트리나 B+트리를 많이 사용하지 않느냐고 의문이 들 수 있는데, 사실 데이터 베이스도 종류에 따라서 여러가지 자료구조를
채택한다(그리고 사실 LSM Tree도 내부적으로 B+ Tree를 부분적으로 차용한 경우도 있다). 그냥 우리가 일반적으로 생각하는 데이터 베이스(Mysql이나 MariaDB 등)가 B+트리를 많이 사용하는 것이고 여기서 말하는 고속 쓰기 워크로드 워크로드란 말 그대로 읽기는 어느정도 수용할 정도의 성능만 되면 되지만, 쓰기 속도가 매우 중요한 워크로드를 말한다. 가령 시계열 데이터라던지, 혹은 정말로 큰 데이터 같은 것들이 있다.
1996년에 LSM Tree를 처음으로 제시한 Patrick O’Neil이 처음 제안한 이 구조는 특히 Transaction History 테이블, 로그 파일, 시계열 데이터 같이 삽입은 매우 빈번하지만 검색은 드문 응용에서 최적화되어 있다. 일단 O’Neil의 원본 논문은 HDD를 기준으로 서술 되었으며(최초의 SSD가 2006년이다) LSM Tree를 사용하면 TPC-A 벤치마크에서 필요한 디스크 암(disk arm)을 기존 50개에서 약 10개로 줄일 수 있어, 시스템 비용을 약 80% 절감할 수 있다고 설명했다.
2. 구조
기본적으로 LSM Tree의 핵심은 서로 다른 저장 매체에 최적화된 여러 컴포넌트로 구성되는 것이다.
서로 다른 매체라고 해봐야, 메모리와 디스크 뿐이지만 큰 구조는 아래와 같다.
1) Memtable
원 논문에서는 C0 tree라고 되어있지만 현대에는 메모리에 적재되어있기 때문에 Memtable 혹은 L0(Level 0)이라고 부르는 구조이다. 보통 Red-Black Tree, Skip List, 또는 B+ Tree로 구현되어있으며 Write Ahead Log 방식으로 기재한다. 즉, 삭제한다고 하더라도 정말 데이터를 지워버리는게 아니라 tombstone으로 표시해두고 이후 Memtable이 모두 꽉 차면 병합시에 해당 값을 지우는 방식이다.
2) SSTable(Single Sorted Table)
원 논문에서는 C1 tree라고 되어있는데 현대에선 일반적으로 L1이라고 부르며 사실 C1 다음에 C2 … Ck 식으로 좀 더 큰 데이터가 저장된다.
C1 및 이후의 하위 레벨의 자료구조를 SSTable(Single Sorted Table)이라고 하며, 디스크에 적재되어있다.
3. Compaction
처음 Memtable에서 지정된 크기나 지정된 노드의 개수가 초과하면 해당 Tree를 C1으로 정렬 병합한다. 이를 Compaction이라고 하는데, 만약 C1에서도 동일하게 지정된 크기나 지정된 노드의 개수를 초과하면 그 다음레벨인 C2에 정렬병합하는식으로 각 하위 레벨로 정렬 병합하는 형태이다.
이러한 Compaction으로 인해 LSM Tree로 이루어진 DB가 간헐적이 성능저하를 일으키며 이 Compaction으로 인한 성능 저하를 줄이기 위해 많은 연구가 있었고, 또 진행되고 있다.
“위에서 개수 혹은 지정된 크기를 넘어가면” 이라고 퉁쳐서 이야기했지만 좀 더 세부적으로 설명하면 아래와 같다.
※ Sorted run
해석하자면 정렬된 연속체이다. 기본적으로 LSM Tree는 정렬된 연속체들로 이루어져 있다고 할 수 있다. 어떤 Sorted run A가 있다고 하면 A 내부의 모든 객체는 정렬된 상태이다. 이러한 Sorted run으로 SSTable이 이루어져있다.
1) Leveled compaction
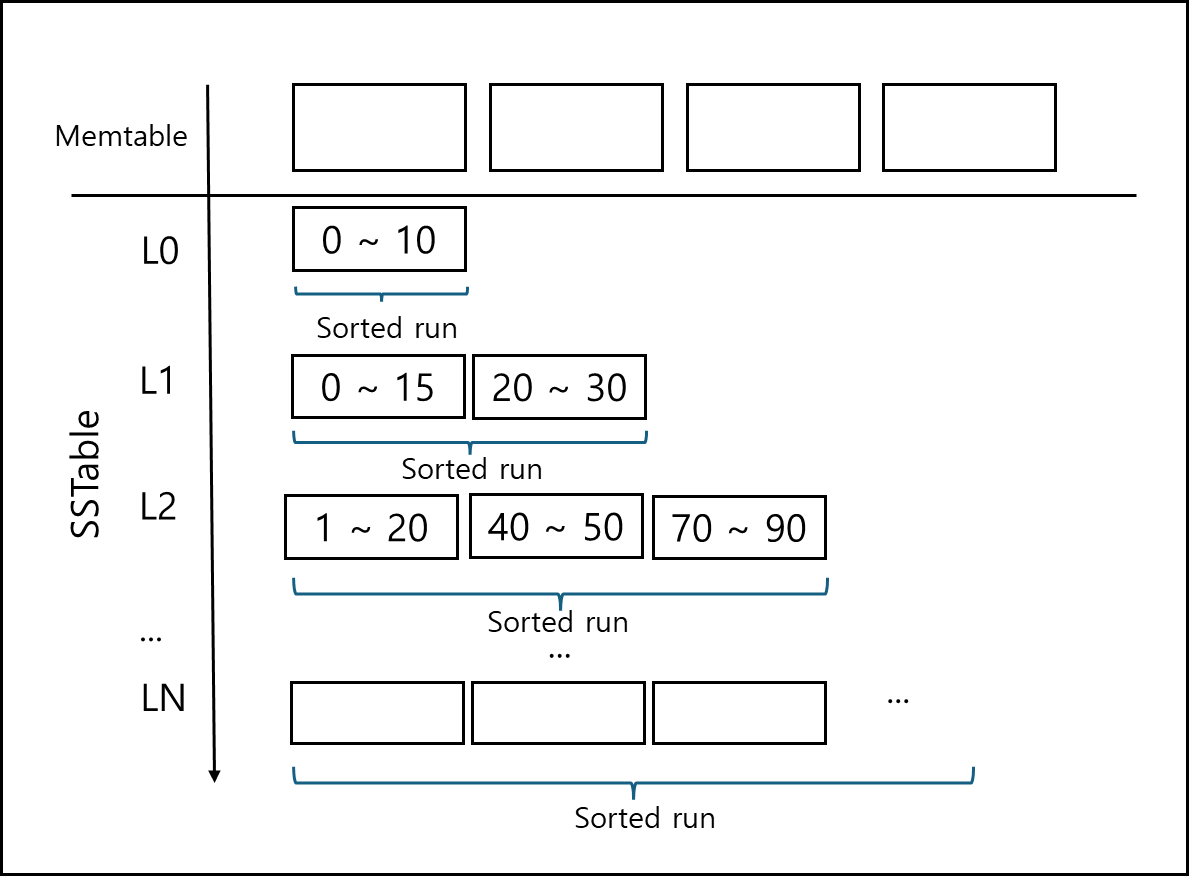
각 레벨은 전역적으로 non-overlapping한 정렬된 sorted run을 유지하는 방식이다. 즉, 한 레벨에 여러 SSTable이 존재할 수는 있지만 그들끼리 키 범위가 겹치지 않는다. 다만, 보통 최상위 레벨(L0)은 예외로 여러 겹침을 허용한다
그림을 보면 아래와 같다.
각각의 레벨에 있는 SSTable들은 모두 키가 겹치지 않는 Sotred run 한 개를 이룬다.
만약에 어떤 Level의 Sorted run 크기가 일정 임계를 넘는다면 그 다음 레벨로 Compaction을 하게 되는데 Compaction 하려는 레벨을 L 라고한다면 L 의 일부 혹은 한개의 SSTable A를 선택하여 L+1에 있는 A와 키 범위가 겹치는 SSTable B를 선택하여 Merge sort후에 겹치지 않게 정리된 SSTable로 L+1에 덮어쓴다.
이렇게되면 동일 레벨 내 SSTable들의 키 범위는 서로 겹치지 않기 때문에 특정 키에 대해서 레벨당 회대 1개의 SSTable만 검사하면 되기 때문에 읽기 성능이 좋다. 다만, Size-Tiered Compaction에 비해서 Compaction이 자주 발생하여 쓰기 처리량이 저하되고 Write stall이 발생할 수 있다.
2) Size-Tiered Compaction
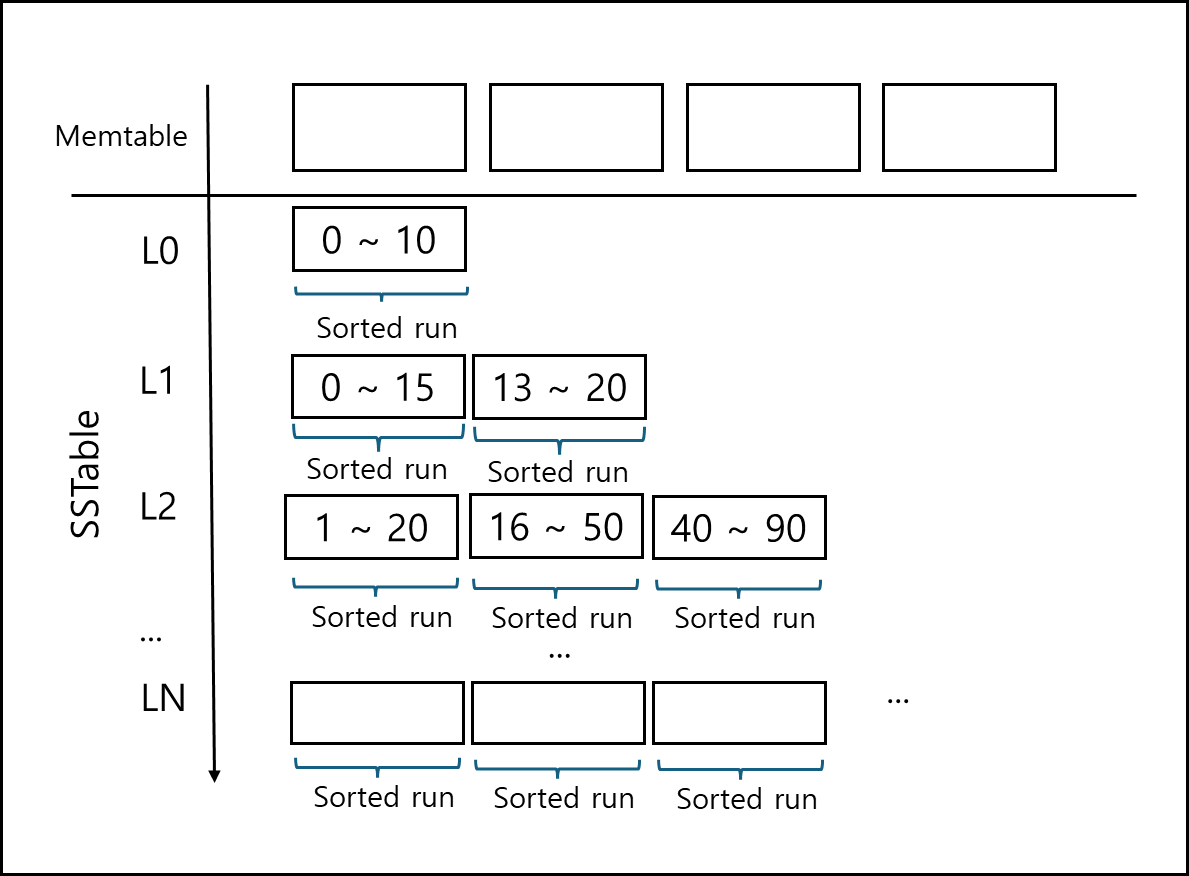
같은 레벨 안에 여러 overlapping sorted runs(즉, 여러 SSTable이 동일 키 범위를 일부 중복하여 가질 수 있음)을 허용한다. 그림으로 보면 아래와 같다.
만약 각 Level에 Sorted run이 일정 개수가 쌓이면 그 레벨 내의 run들을 모두 하나의 Sorted run으로 만들어서 다음 레벨로 이동시킨다.
입력을 쌓았다가 한번에 크게 합치기 때문에 Compaction 빈도가 낮아서 쓰기에는 매우 유리하나, 읽을때 여러 run을 훑어야할 수 있어서 읽기 성능은 상대적으로 떨어지며 각 키가 중복되어 write가 가능하기 때문에 공간 증폭이 증가한다.
3) Universal Compaction
기본적으로 Size-Tiered Compaction의 변형한 형태의 Compaction이라고 보면 된다. Compaction이 시작되면 같은 Level에서 작은 SSTable들을 모아서 병합하는데, 출력 파일의 목표크기를 넘기면 더 파일을 추가하지 않거나 다음 번에 추가 병합을 하여 Sorted run을 하는 방식이다. (특히 Memtable에서 위와 같은 방식으로 다수의 쓰레드를 운용하여 병합하면 성능이 매우 좋아진다.)
이 과정에서 동일한 레벨안에서 중첩된 Key 범위를 병합하므로 완전 non-overlap을 강제하지는 않으나 Size-tiered 방식에 비해서는 당장 병합해야할 파일수는 줄어 든다. 작은 파일들을 보아서 한번에 합치기때문에 쓰기 지연과 write stall은 완화되나 여전히 겹치는 파일을 검색해야해서 랜덤 읽기 성능은 떨어질 수 있으며, Sized-tiered 방식과 동일하게 공간 증폭이 커질 수 있다.
※ 증폭에 대한 개념
1) 읽기 증폭
한 번의 조회에 필요한 디스크 I/O 작업 수를 말한다.
LCS 방식의 경우 특정 키에 대해서 L0 외에 레벨별 1개의 SSTable만 확인하면 되기때문에 Disk I/O가 많지 않지만 STCS 방식의 경우 해당 레벨의 SSTable에 대해서 모두 읽어야하기 때문에 Disk I/O가 많다.
2) 쓰기 증폭
한 바이트의 데이터를 디스크에 유지하기 위해 실제로 디스크에 쓰인 데이터량이다.
아래의 값과 같다.
1
총 디스크 쓰기 바이트 / 애플리케이션에서 쓴 바이트 = 쓰기 증폭
LSM Tree에 쓰려고하는 데이터가 1MB라고 가정했을 때 아래와 같은 상황이라면
- WAL: +1MB
- Memtable flush: +1MB
- Compaction (3 레벨 통과): +3MB
총 쓰기는 6MB로 쓰기 증폭은 6이 되는 셈이다. 만약 쓰기 증폭이 높으면 디스크 대역폭이 압박되어 읽기 성능도 악화됩니다
3) 공간 증폭
디스크에 저장된 실제 데이터 크기 / 논리적 데이터 크기를 말한다.
그냥 데이터를 기재하는 만큼 디스크에 공간을 차지하는거 아닌가 싶겠지만 그렇진 않다. 오래된 버전의 데이터 (tombstone, 삭제 마커 미정리)나 Compaction 중 임시로 필요한 공간 역시 필요한 공간에 포함되기 때문에 대략 1.x배에서 2배 이상 공간이 필요하게 된다.
※ 추가 업데이트 예정
참고 자료
- 위키피디아 - Log-structured merge-tree
- O’Neil, Patrick, Edward, Cheng, Dieter, Gawlick, and Elizabeth, O’Neil. “The log-structured merge-tree (LSM-tree)”.Acta Inf. 33, no.4 (1996): 351–385.
- Liu, Junfeng, Fan, Wang, Dingheng, Mo, and Siqiang, Luo. “Structural Designs Meet Optimality: Exploring Optimized LSM-tree Structures in a Colossal Configuration Space”.Proc. ACM Manag. Data 2, no.3 (2024).
- Byun, Hongsu, Honghyeon, Yoo, and Sungyong, Park. “Revisiting Multi-threaded Compaction in LSM-trees: Enabling Compaction Pipelining.” . In Proceedings of the 54th International Conference on Parallel Processing (pp. 794–803). Association for Computing Machinery, 2025.