동적 계획법
동적 계획법
영어로는 dynamic programming이라고 불린다. 복잡한 문제를 풀기 위해 작은 여러 문제로 나눠서 푸는 것이다. 작은 여러 문제를 해결하고 그 해결한 결과를 취합하여 복잡한 문제 결과를 내는데 사용한다.
동적 계획법을 사용하기 위한 조건
1.중복되는 부분 문제(Overlapping Subproblems)
DP는 기본적으로 문제를 나누고 그 문제의 결과 값을 재활용해서 전체 답을 구한다. 그래서 동일한 작은 문제들이 반복하여 나타나는 경우에 사용이 가능하다.
예를 들어 n번째 피보나치 수열을 구한다고 해보자, 피보나치 수열의 공식은 아래와 같다.
1
2
n <= 2 : 1
n > 2 : f(n) = f(n-1) + f(n-2)
n을 구하기 위해 n-1번(단 n>1)이 필요하므로 부분 문제들로 이루어져있다.
1
2
3
4
f(3) = f(2) + f(1)
f(4) = f(3) + f(2)
f(5) = f(4) + f(3)
......
값을 한번 구하면 1번은 더 쓸수 있게 되어있다. 따라서 작은 문제들의 결과를 더하면 이후 값에 재사용할 수 있다. 이런 경우 중복되는 부분 문제라고 할 수 있다.
2. 최적 부분 구조(Optimal Substructure)
부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 낼 수 있는 경우 사용이 가능하다.
예를 들어 다음과 같은 상황에서 최단 경로를 구한다고 가정해보자
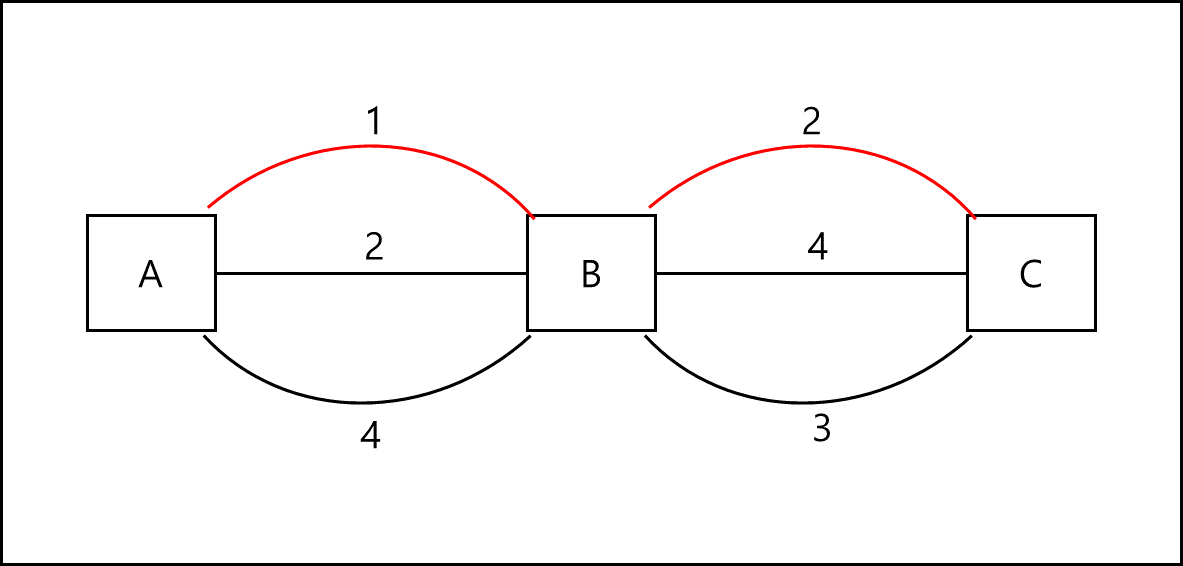
A에서 C로 가는 가장 작은 가중치의 경로는 A에서 B로 가는 가장 작은 가중치 경로를 포함하고 있다 즉,
동적 계획법 방식
1. Top-Down (Memoization 방식)
큰 문제를 작은 부분 문제로 나누어 해결하는 방식이다. 작은 부분 문제로 나누기 위해서 재귀 함수를 사용하여 문제를 작은 부분 문제들로 쪼갠 뒤 중복 계산을 피하기 위해 이전에 계산한 값을 저장하여 확인한다.
2. Bottom-Up (Tabulation 방식)
작은 부분부터 차례로 해결해서 전체 문제를 해결하는 방식이다. 반복문을 이용하여 작은 문제들을 반복적을 구하고 구한 것을 메모리에 저장하여 전체 결과를 구할때 사용한다.
동적 계획법을 사용하는 예시
- 최장 공통 부분 수열
- Cocke-Younger-Kasami (CYK) 알고리즘
- 비터비 알고리즘
- Earley algorithm
- 벨먼-포드 알고리즘
- 다익스트라 알고리즘
- 플로이드-워셜 알고리즘
- chain matrix multiplication의 최적 곱셈 순서
- 부분집합 합 알고리즘
- 배낭 문제