벡터 1
벡터에 대해서 물리적 벡터와, 수학적인 벡터로 나눠서 설명 하도록 하겠다.
물리적 벡터
벡터는 원래 물리에서 시작된 개념이다. 시작점과 종결점이 중요한게 아니라 방향과 크기만 같으면 동일한 벡터로 간주한다.
1. 벡터와 좌표계
(1) 평면 벡터
이차원 평면에서 크기(스칼라)와 방향을 포함한 표현 도구이다.
(2) 공간 벡터
삼차원 공간에서 크기(스칼라)와 방향을 포함한 표현 도구이다.

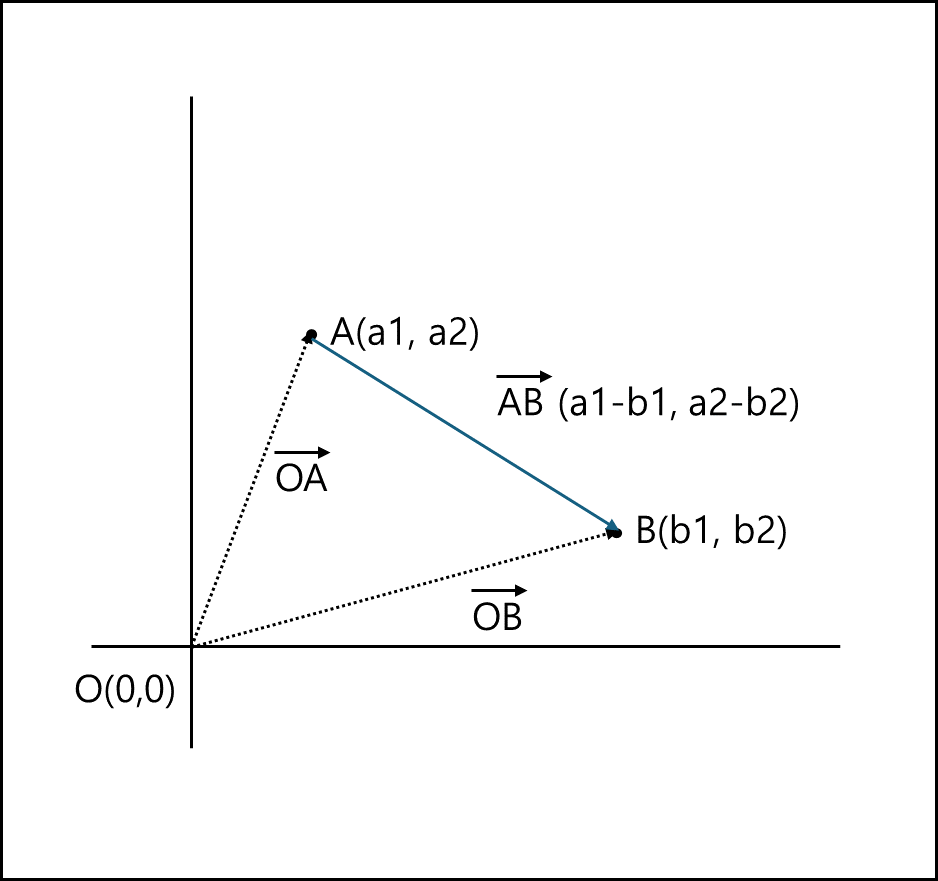
(3) n차원 벡터
$R^{n}$상의 벡터 $v=(v_{1},v_{2},…,v_{n})$ $= \overrightarrow{AB} = (b_{1}-a_{1},b_{2}-a_{2},…b_{n}-a_{n})$
2. 벡터의 연산
(1) 노름
벡터의 크기라고도 하며 다음과 같은 수식으로 산출한다.
$\left| v \right| = \sqrt{v_{1}^2+v_{2}^2+…+v_{n}^2}$노름이 1인 벡터를 단위 벡터라고 한다.
어떤 벡터를 단위 벡터로 만드는 것을 정규화라고 한다. 이러한 정규화를 하는 수식은 다음과 같다. \(\widehat{v} = \frac{\overrightarrow{v}}{\left\| \overrightarrow{v} \right\|} = \left ( \frac{x}{\left\| \overrightarrow{v} \right\|},\frac{y}{\left\| \overrightarrow{v} \right\|},\frac{z}{\left\| \overrightarrow{v} \right\|} \right ) = \left ( \frac{x}{\sqrt{x^{2}+y^{2}+z^{2}}},\frac{y}{\sqrt{x^{2}+y^{2}+z^{2}}},\frac{z}{\sqrt{x^{2}+y^{2}+z^{2}}} \right )\)
$e_{1}=(1,0,…,0), e_{2}=(0,1,…,0)$등을 표준 단위 벡터라고 한다.
(2) 선형결합
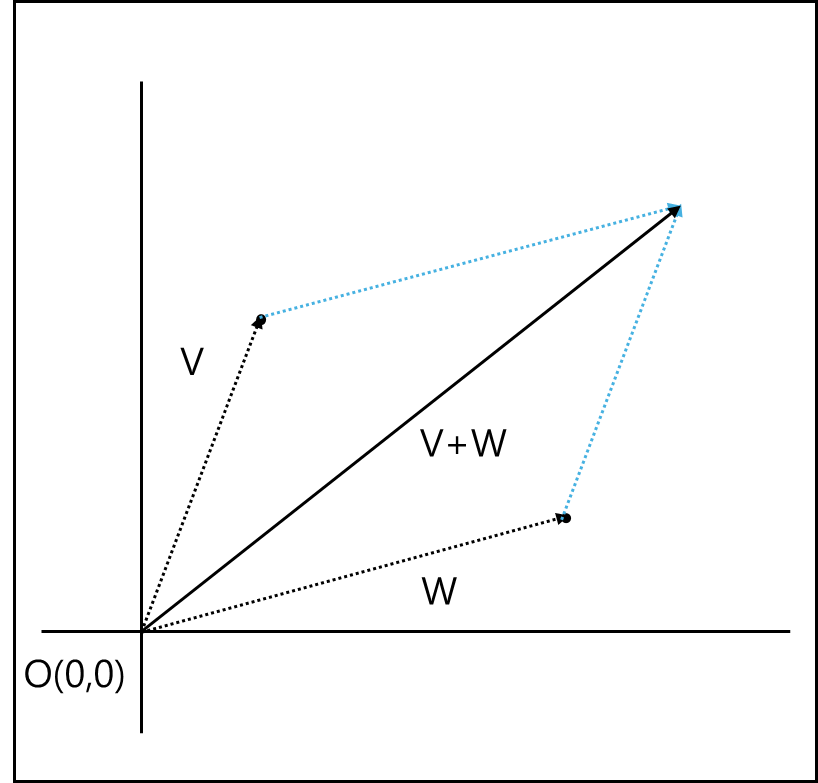
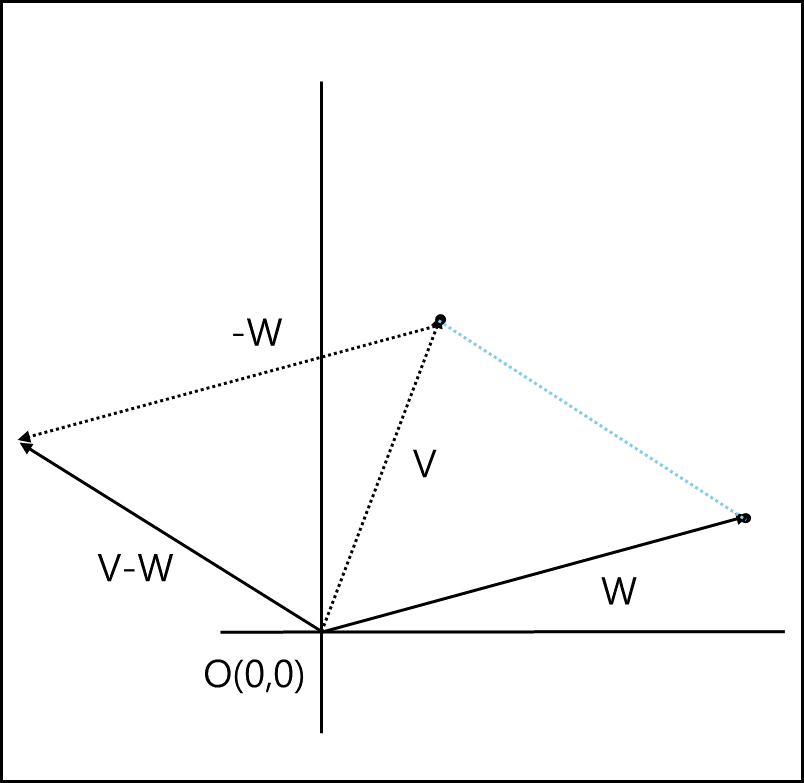
1) 벡터의 덧셈, 뺄셈
벡터의 각각 요소를 더하거나 빼서 계산한다.
\(v\pm w = (v_{1}\pm w_{1},...,v_{n}\pm w_{n})\)
2) 벡터의 실수배
벡터의 각 요소를 k만큼 곱한다.
\(kv = (kv_{1},kv_{2},...,kv_{n})\)
3) 선형 일차 결합
$R^{n}$의 벡터 w가 임의의 실수 $k_{1},k_{2},…,k_{r}$에 대하여
$ w=k_{1}v_{1}+k_{2}v_{2}+…+k_{r}v_{r} $
의 형태로 쓰여졌다면 w를 $v_{1},v_{2},…,v_{r}$의 선형 일차 결합이라고 한다.
(3) 스칼라곱
한 벡터가 다른 벡터의 방향에 대해 가한 힘에 의해 변화된 크기(스칼라). 점곱 혹은 내적이라고 부름
\(v\cdot w = \left\| v \right\| \left\| w \right\| cos\Theta = v_{1}w_{1}+v_{2}w_{2}+...+v_{n}w_{n}\) (단 여기서 $\Theta $는 두 벡터 w,w가 이루는 각)
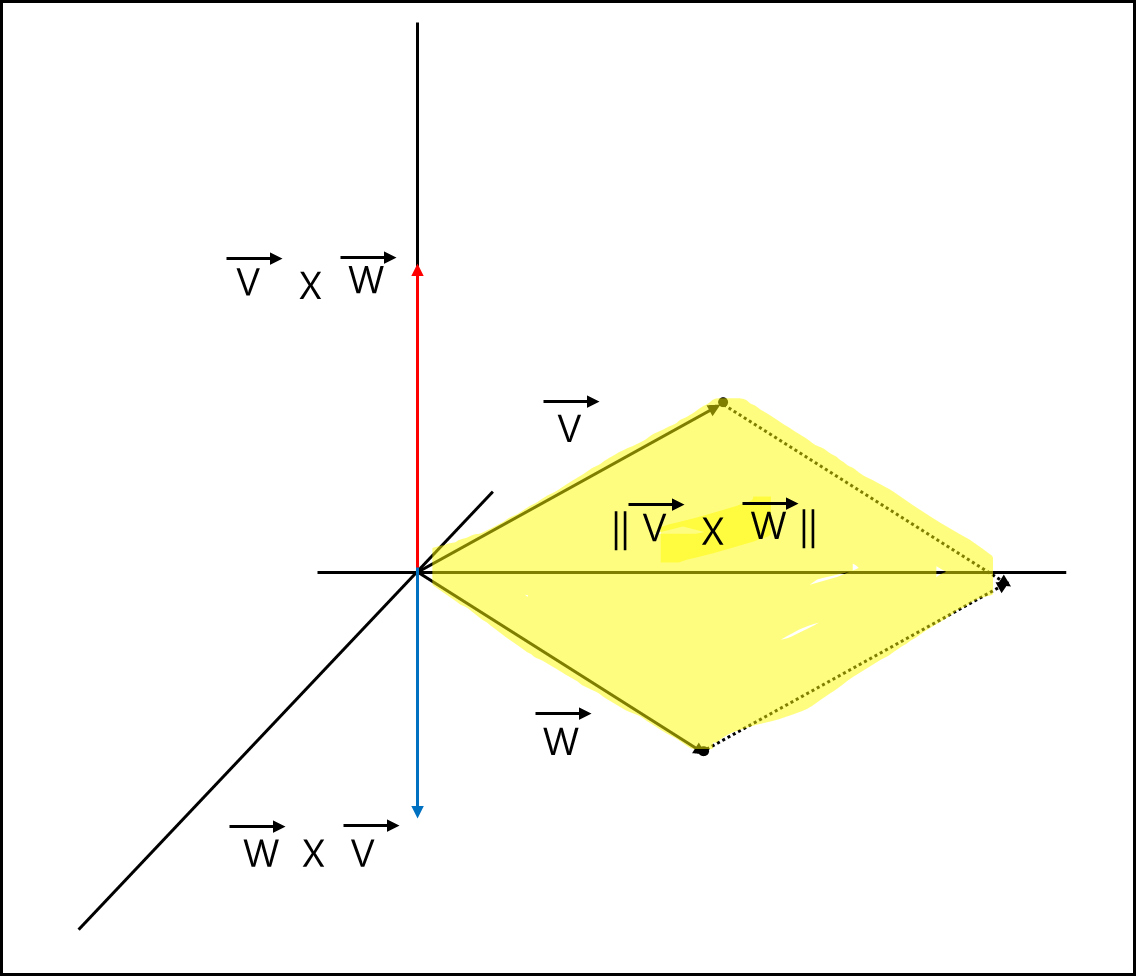
(4) 벡터곱
방향은 두 벡터에 동시에 수직이고, 크기는 두 벡터의 평행사변형의 면적인 $R^{3}$상의 벡터 가위곱 또는 외적 \(V\times W = \begin{pmatrix} \begin{vmatrix} v_{2} & v_{3} \\ w_{2} & w_{3} \\ \end{vmatrix} &, - \begin{vmatrix} v_{1} & v_{3} \\ w_{1} & w_{3} \\ \end{vmatrix} &, \begin{vmatrix} v_{1} & v_{2} \\ w_{1} & w_{2} \\ \end{vmatrix} \\ \end{pmatrix}\)
벡터 곱의 노름 값은 $ \left| \overrightarrow{V} \times \overrightarrow{V} \right|$나 $ \left| \overrightarrow{V} \times \overrightarrow{V} \right|$나 같으나 벡터 곱의 방향은 어느 벡터를 앞에 두느냐에 따라 180도가 달라진다. 외우기 어렵다면 오른손 법칙을 생각하면 편해진다. 먼저 나오는 벡터를 네 손가락으로 생각하고 감아쥘때 엄지손가락 방향이 벡터 곱의 방향이다.
3. 벡터의 응용
(1) 직선의 표현
이차원 평면, 혹은 3차원 공간에서의 위치 벡터가 a인 점 A를 지나며 방향벡터가 v인 직선상의 임의의 점 X의 위치벡터 x는 \(x=a + kv\) 을 만족한다. (단, k는 임의의 실수)
(2) 평면의 표현
3차원 공간에서 위치 벡터가 a인 점 A를 지나며 법선벡터가 v인 평면상의 임의의 점 X의 위치벡터 x는 \((x-a)\cdot v = 0\) 을 만족한다.
여기서 법선 벡터를 나타내기 위해서는 평면상의 서로 다른 직선의 두 방향 벡터의 벡터곱으로 구하면 용이하다.