부동소수점 표현
부동 소수점 표현
1. 개요
최근 AI가 발달하면서 부동 소수점 표현이 중요해지고 있다.
부동 소수점은 정밀도에 따라 데이터 크기가 달라진다.
2. 정밀도
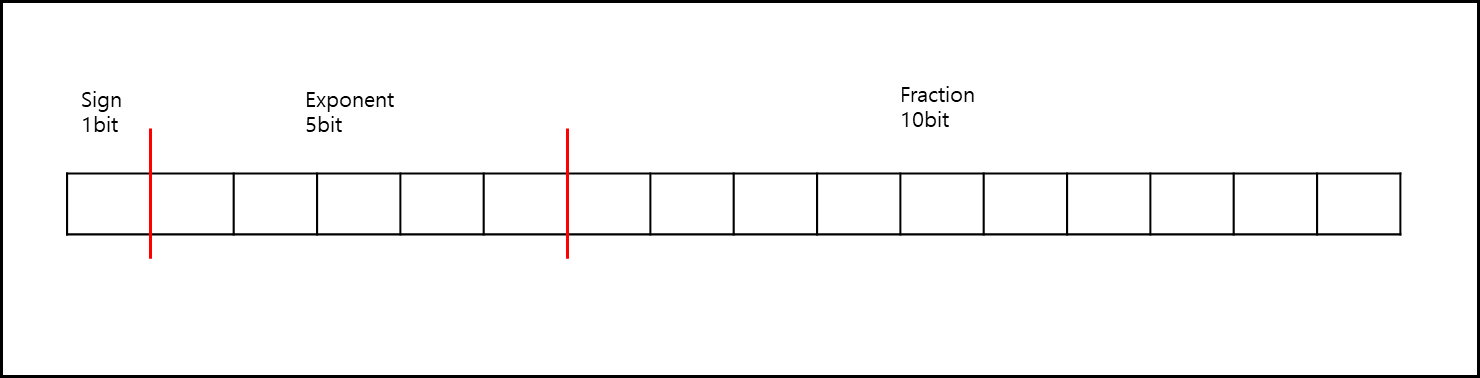
1) Half precision
수 하나당 2bytes를 사용하는 표기법이다.
부호 : 1bit
지수부 : 5bit
소수부 : 10bit
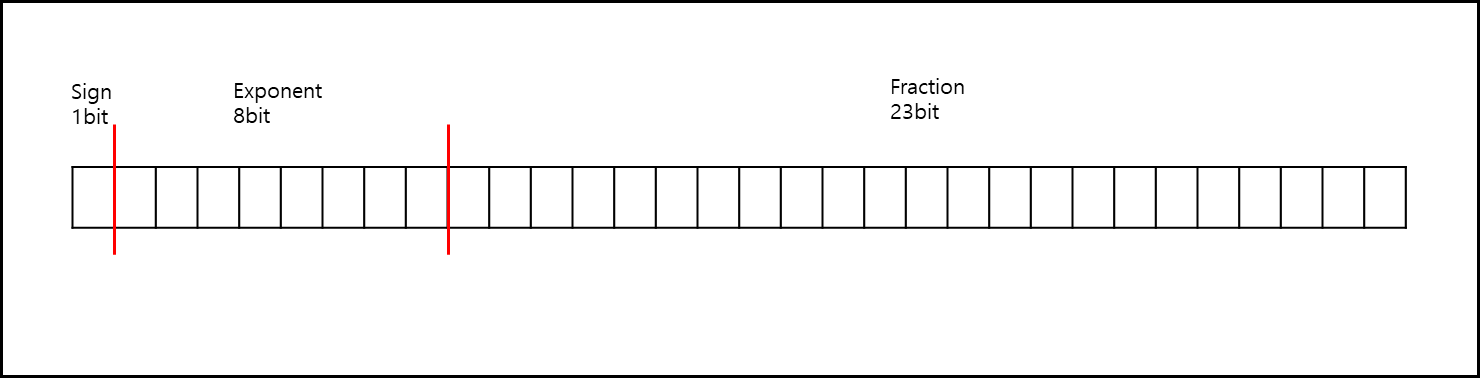
2) Single precision
수 하나당 4bytes를 사용하는 표기법이다.
부호 : 1bit
지수부 : 8bit
소수부 : 23bit
3) Double precision
수 하나당 8bytes를 사용하는 표기법이다.
부호 : 1bit
지수부 : 11bit
소수부 : 52bit
3. 환산법
기본적으로 환산은 아래의 공식을 따른다.
\[(-1)^{S}*(1.fraction)*2^{exponent + bias}\]S는 처음 부호 1bit를 말한다.
양수는 0, 음수는 1이다.
1.fraction은 소수부이지만 0이 아닌값이 소수점 위로 올라간 형태이다.
아래의 값을 보자.
이런 소수가 있을때 1.fraction은 아래와 같이 표현 할 수 있다.
\[1.1001100_{2} \times 2^{-3}\]이런식으로 0이 아닌 값을 소수점 위로 올린 값이다. 0이 아닌 값은 1로 넘기는 것이다. 위 식에서 -3이 exponent의 역할을 하게 된다.
그렇다면 bias는 뭘까?
이는 편향값으로 half, single, double 모두 각각의 편향값을 갖고 있다.
이 값을 exponent에 더해주면 된다.
half는 15
single은 127
double은 1023
4. 예시
1) 0.75
0.75를 세가지 정밀도로 각각 표현해보겠다.
가장 먼저해야할 건 0.75의 소수부를 이진수로 변환하는 것이다.
2를 곱해서 정수부의 값을 쓰면 된다.
1
2
3
↓ 0.25
2x 0.5 0
2x 1.0 1
소수부는 아래와 같다.
1
0.01
이 값은 아래의 값으로 변환할 수 있다.
\[(-1)^{0}\times (1.0) \times 2^{-2+bias}\]각 표현법에 따른 bias를 더하여 각기 환산하면 아래와 같다.
a. half
\((-1)^{0}\times (1.0) \times 2^{13}\)
부호부 : 0 지수부 : $2^{13}$ => 13의 이진수 => 1101 소수부 : 01000000….
1
0 00110 0100000000
b. single
\((-1)^{0}\times (1.0) \times 2^{125}\)
부호부 : 0 지수부 : $2^{125}$ => 125의 이진수 => 01111101 소수부 : 01000000….
1
0 01111101 0100000000....
c. double
\((-1)^{0}\times (1.0) \times 2^{1021}\)
부호부 : 0 지수부 : $2^{1021}$ => 1021의 이진수 => 0011 1111 1101 소수부 : 01000000….
1
0 01111111101 0100000000
2) $ 1.1_{10} $
십진수로 1.1을 이진수로 세가지로 각각 변환해보겠다. 일단 가장 먼저해야할 건 1.1의 소수부를 이진수로 변환하는 것이다.
2를 곱해서 정수부의 값을 쓰면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
↓ 0.1 (소수부만)
2x 0.2 0
2x 0.4 0
2x 0.8 0
2x 1.6 1
2x 1.2 1
2x 0.4 0
2x 0.8 0
2x 1.6 1
2x 1.2 1
2x 0.4 0
2x 0.8 0
2x 1.6 1
2x 1.2 1
... ...
기본적으로 무한 소수이다.
따라서 소수부는 아래와 같다.
위 값을 정수부랑 더하면 아래와 같다.
\[1.0001100110011\]이 값은 아래의 값으로 변환할 수 있다.
\[(-1)^{0}\times (1.00011001100...) \times 2^{0+bias}\]각 표현법에 따른 bias를 더하여 각기 환산하면 아래와 같다.
a. half
\((-1)^{0}\times (1.00011001100...) \times 2^{15}\)
부호부 : 0
지수부 : $2^{15}$ => 15의 이진수 => 1111
소수부 : 00011001100…
1
0 01111 0001100110
b. single
\((-1)^{0}\times (1.00011001100...) \times 2^{127}\)
부호부 : 0
지수부 : $2^{127}$ => 127의 이진수 => 0111 1111
소수부 : 00011001100…
1
0 01111111 00011 00110 01100 11001 101
c. double
\((-1)^{0}\times (1.00011001100...) \times 2^{1023}\)
부호부 : 0
지수부 : $2^{1023}$ => 1023 이진수 => 0011 1111 1111
소수부 : 00011001100…
1
0 001111111111 00011 00110 01100 11001 10011 00110 01100 11001 10011 00110 10
※ 반올림
그렇다, 소수부 표현 bit 수가 넘어가면 반올림 처리를 해줘야한다.
그런데 이게 아주 보통문제가 아니다.
이를 처리하기 위해선 GRS가 필요한데 이는 반올림시 사용되는 보조 비트세트이다.
- Guard 비트 (G): 정규화된 수의 유효숫자 부분 중 가장 마지막 비트 바로 오른쪽에 위치하는 비트이다.
- Round 비트 (R): Guard 비트 바로 오른쪽에 위치하는 비트이다.
- Sticky 비트 (S): Round 뒤의 모든 bit를 OR한 값이다.
여기서 총 3가지 부류로 나뉜다.
| GRS | 설명 |
| 0xx | 내림 |
| 100 | G비트 이전 비트가 1이면 올림, 아니면 내림. 즉 LSB가 0이 되도록 설정 |
| 1xx | 올림 |
※ 100% 확실한건 아니니 출처를 참고하기 바란다.