Post

블룸 필터(Bloom Filter)

Posted
By Blake Woo 8 min read

블름 필터(Bloom Filter)

1. 개요

블룸필터는 1970년 Burton Howard Bloom이 제안한 확률론적(probabilistic) 데이터 구조로, 어떤 원소가 집합에 속할 수도 있다(false positive 가능) 또는 확실히 속하지 않는다(false negative 불가능)는 반환이 가능한 구조이다. 메모리 효율성과 연산 속도의 탁월한 균형으로 인해, 대규모 데이터 처리 시스템에서 널리 사용되고 있다.

2. 구조

1) 삽입

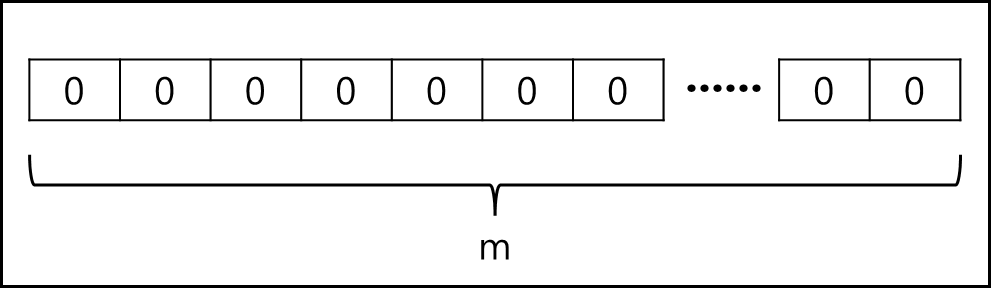
먼저 m개의 비트 배열을 정의한다. 이 배열은 모두 0으로 세팅되어있다.

img.png

여기서 k개의 독립적인 해시 함수가 필요한데, 일단 설명간에는 3개의 해시함수 f, g, h로 설명하겠다.
여기서 해시함수들은 동일한 값을 해시하게 되는데 각각 다른 결과 값이 나오는 함수면 좋다.

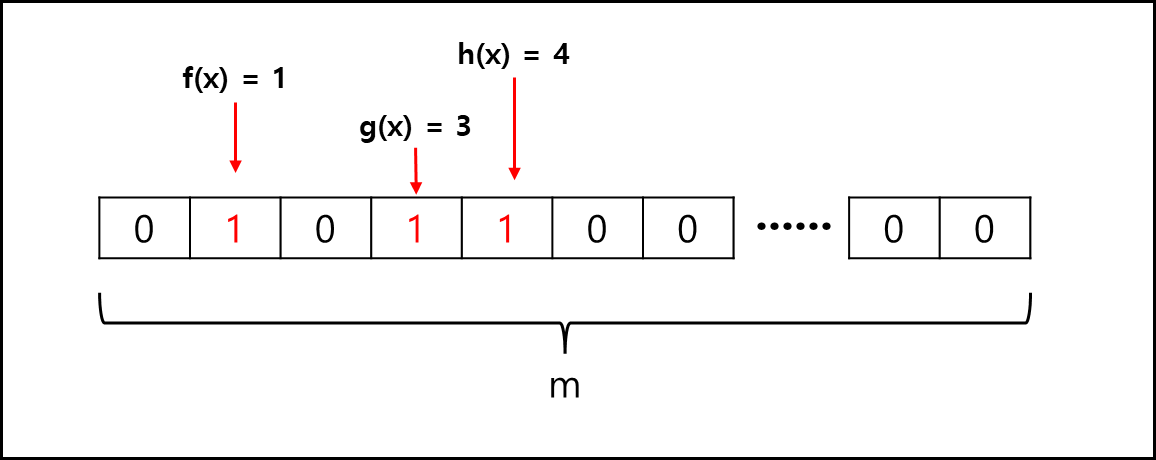
어떤 값 x가 입력되었다고 해보자. 그러면 k개의 해시 함수(여기서는 f,g,h 3개다)를 적용하게되는데 그러면 bit 배열에 대해서 index로 사용할 수 있는 값 k개(예시에서는 3개)가 나온다.
이렇게 나온 index k개(여기서는 3개)에 해당하는 bit를 1로 세팅한다.

img_1.png

2) 조회

이미 삽입 처리가 된 m개의 비트배열이 있을 때 어떤값 y가 있는지 확인해야 할 때는 삽입때와 마찬가지로 k개의 해시함수를 이용하여 index k개를 구한다.
이후 비트배열의 해당 index에 가서 값을 확인해보는데, k개 모두 1이라면 y값이 있을 수 있다(없을 수도 있다는 뜻이다) 하지만 k개 중에 하나라도 0이라면 y값이 없는 것은 확실하다.

img_2.png

※ 삭제는 없는가?

원래 클래식한 bloom filter의 경우 삭제 연산을 지원하지 않는다. 이는 bit로만 해당 값들을 체크하기 때문이다.
이를 해결하기 위한 알고리즘이 있으며 아래의 파생 구조에 설명되어있다.

※ m값, k값 정하기

이론적으로 원하는 false positive rate ε를 달성하려면 비트 배열의 크기 m값과 해시함수 개수 k값은 아래와 같이 설정하는 것이 좋다.

\[m = - \frac{nln\epsilon}{(ln2)^{2}}\] \[k = \frac{m}{n}ln2 \approx 1.386 log_{2}(\frac{1}{\epsilon})\]

1% false positive rate를 원한다면 원소당 약 9.6비트가 필요하고, 이를 10배 감소시키려면 원소당 약 4.8비트만 추가하면 된다.

하지만 블룸필터 이론의 중요한 가정은 k개 해시함수가 서로 독립적이어야 한다는 것인데, 그러나 실제 구현에서는 아래의 문제가 있다.

  • 완벽한 독립성 달성 어려움: 실무 해시함수(MurmurHash, SHA-1 등)는 완전한 독립성을 보장하지 않는다.
  • 파라미터 선택 오류: 많은 구현이 k를 3 이상으로 설정해도 실제 성능 개선이 미미하다.
  • 해시값 분포: 특정 범위의 입력에 대해 비균등 분포를 보일 수 있다.

따라서 실제 시스템에서는 k=2~4 범위에서 실험적으로 최적값을 찾는 것이 권장된다.

3. 파생 데이터 구조

1) Counting Bloom Filter

위에서 언급했듯이 클래식한 블룸필터는 삭제 연산을 지원하지 않는다. 단순히 비트를 0으로 설정하면 false negative가 발생하기 때문이다. 이를 해결하기 위해 2000년 Li Fan 등이 제안한 방식은 비트 배열 대신 m개의 카운터 배열을 사용한다.

2) Scalable Bloom Filter

고정된 용량의 블룸필터는 원소 추가에 따라 false positive rate가 선형으로 증가하는데, Scalable Bloom Filter는 용량에 도달할 때마다 확장 계수(보통 2배)로 새로운 필터를 생성하여 동적 스케일링을 지원한다.

조회 시에는 모든 부분 필터를 검사해야 하므로, 시간 복잡도는 O(k log₂(n))이 되지만, false positive rate를 일정하게 유지할 수 있다.

3) One-Hashing Bloom Filter

k개의 독립적인 해시함수 구현은 계산 오버헤드가 크다. One-Hashing Bloom Filter는 단일 해시함수에서 도출된 k개 해시값을 modulo 연산으로 생성하여, 거의 동등한 false positive rate를 유지하면서 해시 계산을 최적화한다.

4. 사용 예시

| 응용 분야 | 사용 예시 | 효과 | | ——– | ——————————————— | ——————————————- | | 보안 | Google Safe Browsing (악성 URL 감지) | 외부 API 호출 제거, false positive 시에만 full check | | 캐시 최적화 | Akamai CDN (one-hit-wonder 필터링) | 캐시 공간 75% 절감 | | 금융 사기 탐지 | 신용카드-가맹점 거래 | 61GB 대비 98% 메모리 절감 | | 광고 중복 제거 | 사용자별 광고 노출 기록 | 대규모 사용자 집단에서 O(1) 조회 | | 데이터베이스 | LSM 트리 (Cassandra, RocksDB) | SSTable 불필요한 디스크 I/O 제거 | | 중복 탐지 | 로그 처리, 스트림 분석 | retention window 초과 데이터도 중복 감지 가능 |

참고 자료

  • 위키백과 - Bloom filter
  • https://systemdesign.one/bloom-filters-explained/
  • Prosenjit Bose, , Hua Guo, Evangelos Kranakis, Anil Maheshwari, Pat Morin, Jason Morrison, Michiel Smid, and Yihui Tang. “On the false-positive rate of Bloom filters”.Information Processing Letters 108, no.4 (2008): 210-213.
  • Choi, Eunji; Lee, Jungwon; Yim, Changhoon; Lim, Hyesook (2024). “Decoding Errors in Difference-Invertible Bloom Filters: Analysis and Resolution”. IEEE Access. 12: 40622–40633.
  • Paulo Sérgio Almeida, , Carlos Baquero, Nuno Preguiça, and David Hutchison. “Scalable Bloom Filters”.Information Processing Letters 101, no.6 (2007): 255-261.
  • Lu, Jianyuan, Tong, Yang, Yi, Wang, Huichen, Dai, Linxiao, Jin, Haoyu, Song, and Bin, Liu. “One-hashing bloom filter.” . In 2015 IEEE 23rd International Symposium on Quality of Service (IWQoS) (pp. 289-298).2015.
Algorithm
Computer science Algorithm
This post is licensed under CC BY 4.0 by the author.