알파 베타 가지치기
알파 베타 가지치기
이전의 Minimax 알고리즘으로 전체 경우의 수를 탐색 할 수 있다면 어떤 게임에서도 이길 수 있다고 했다.
그리고 체스만 하더라도 경우의 수가 너무 많기 때문에 전체 탐색을 할 경우 너무 많은 시간이 걸리기 때문에 탐색 깊이 제한을 둬서 응답 시간을 줄이는 방법을 사용한다고 했다.
그런데 굳이 탐색할 필요 없는 부분을 애시당초 탐색하지 않으면 더 시간이 줄지 않을까? 이런 생각에서 시작한 방법이 바로 알파 베타 가지치기(alpha beta pruning)이다.
이 알파 베타 가지치기를 설명하기 위해서는 예시를 드는 것이 편하므로 이전에 미니 맥스 알고리즘을 설명할 때 썼던 그림을 갖고 와서 조금 바꿔서 설명하겠다.
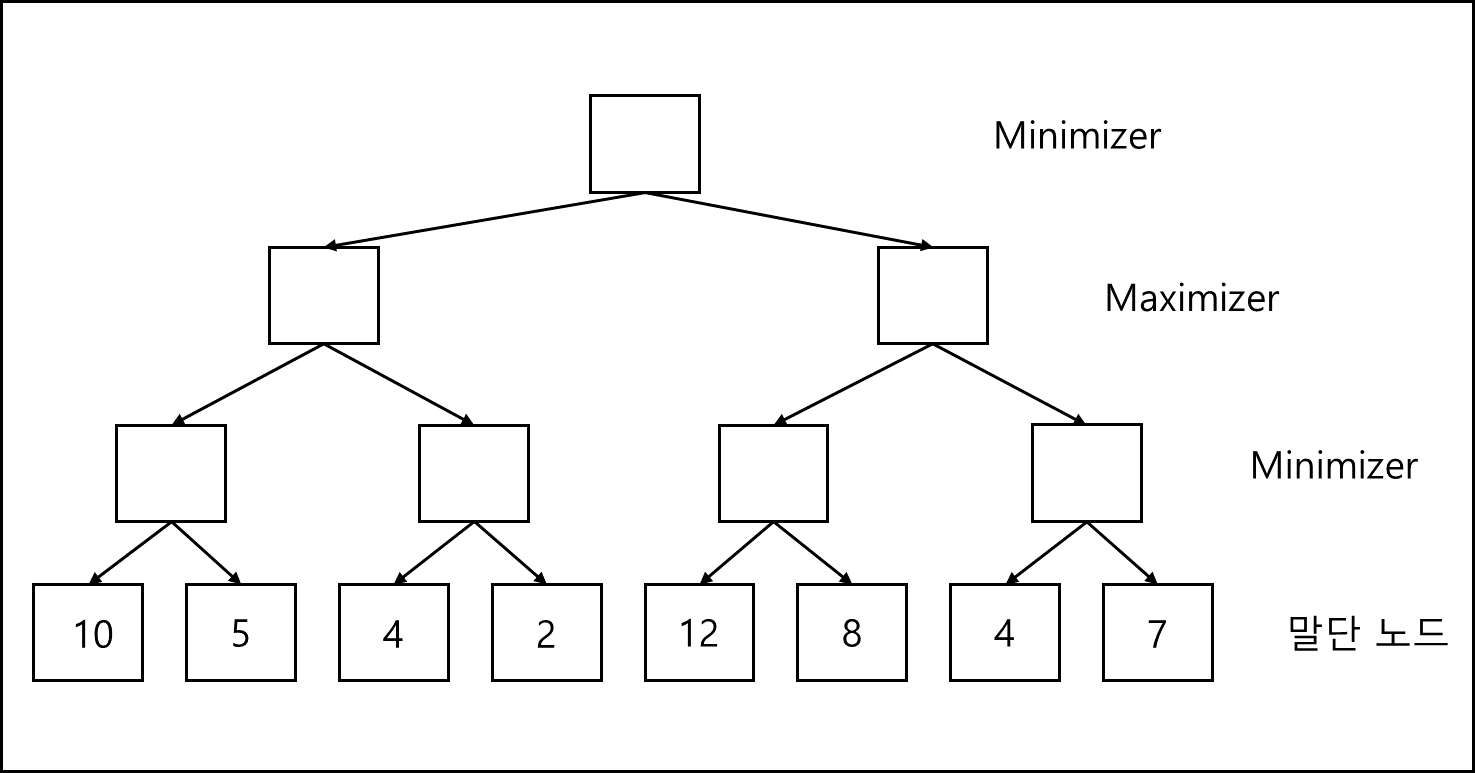
다음과 같이 말단 노드가 평가 함수로 평가된 값이 기재된 트리가 있다고 가정해보자. 이러한 단말 노드는 내림차순으로 정렬되어있다. 그렇다면 이 경우에 minimax 알고리즘에 따르면 모든 말단 노드에서 부모 노드로 값을 올린다. 다음과 같은 경우에는 바로 위 부모노드가 Minimizer이므로 아래와 같이 올라 간다.
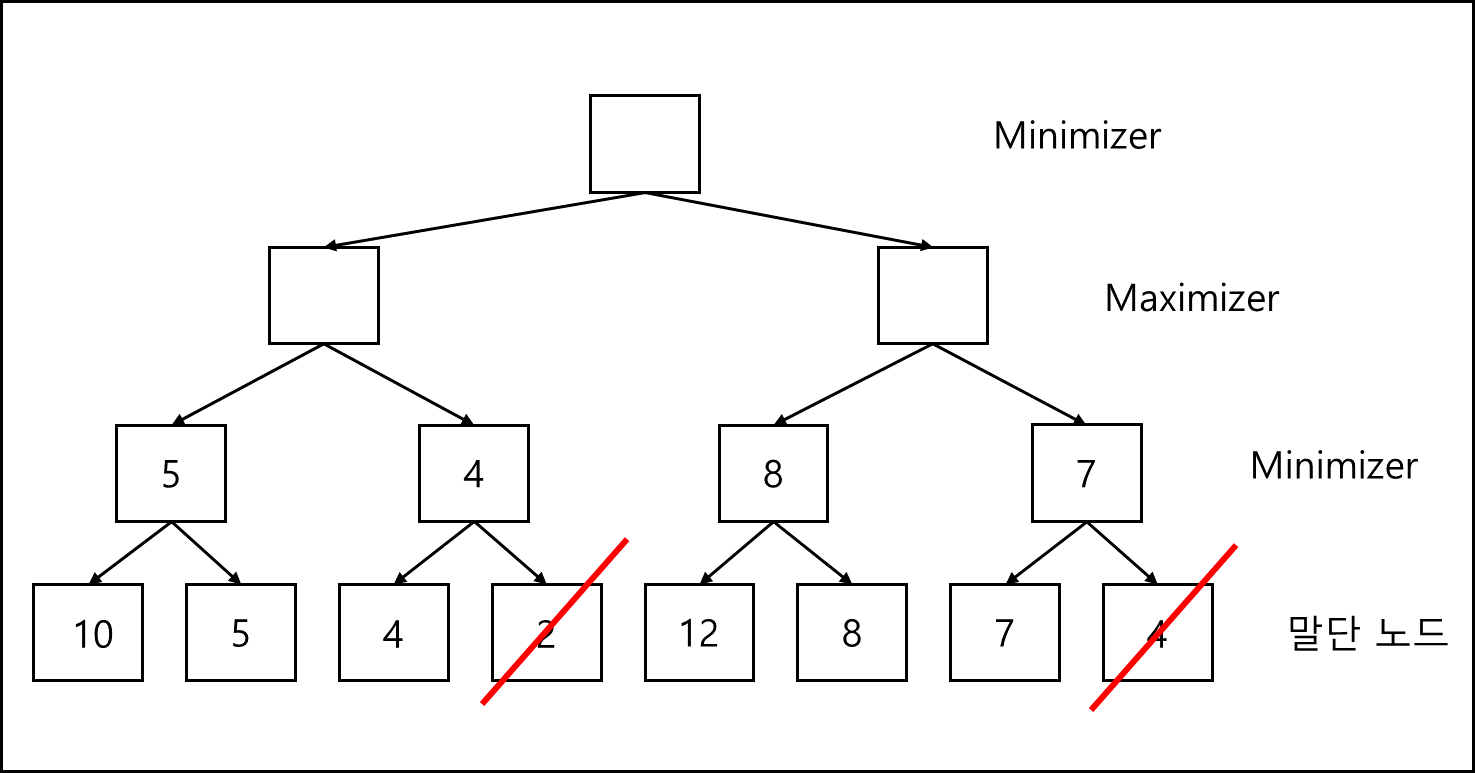
위의 그림을 보면 각각 2와 4에 붉은 색으로 빗금이 그여있는걸 볼 수 있는데 이렇게 노드의 탐색을 배제하는게 알파베타 가지치기이다. 아무 탐색이나 배제해서 되는게 아니고 실질적인 절차는 아래와 같다.
- 이전 노드의 최소 값이 5로 지정되었다.
- 그 다음은 max 값이 올라올 차례인데 이미 4 이하의 값 밖에 없다.
- 따라서 그다음 탐색은 배제하여 탐색량을 줄인다.
이러한 탐색을 말단 노드부터 루트 노드로 올라가면서 재귀적으로 진행함으로써 전체 탐색량을 줄이는 식이다.
위의 그림에선 탐색량이 별로 줄어든 것 같이 보이진 않지만 실제로 이렇게 알파 베타 가지치기를 진행했을경우에 오목의 경우 해당 논문 ( 게임 트리와 알파-베타 가지치기를 이용한 오목 프로그램의 설계 및 구현 )에 따르면 알파-베타 가지치기는 대략 30% 이상의 가지치기 효율을 기대할 수 있다고 한다.