유클리드 호제법(Euclidean algorithm)

유클리드 호제법(Euclidean algorithm)

그냥 기본 알고리즘 리마인드 겸 포스팅하는 것이다.

1. 개요

간단히 말해서 두 자연수 간의 최대공약수를 찾는 알고리즘이다.
명시적으로 기술된 가장 오래된 알고리즘으로서도 알려져 있으며, 기원전 300년경에 쓰인 《원론》 제7권, 명제 1부터 3까지에 해당한다.

2. 방법

방법은 매우 간단하다.

1. 입력으로 자연수 두 개가 들어온다.
2. 만약 입력으로 들어온 자연수가 같으면 둘 중 어느것이든 반환하고 종료한다.
3. 두 자연수 중 작은 것을 a, 큰 것을 b라고 정의할 때 b가 0이면 a를 반환하고 종료한다.
4. b이 a로 나누어 떨어지면, a를 출력하고 알고리즘을 종료한다.
5. 그렇지 않으면, b을 a로 나눈 나머지를 새롭게 b에 대입하고, b과 a를 바꾸고 4번으로 돌아온다.

그냥 읽었을 때 어렵진 않은데 뭐지 싶을순 있다.
가장 직관적인 그림이 있다. 아래의 그림을 보자.

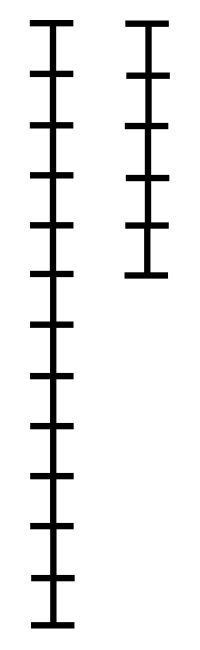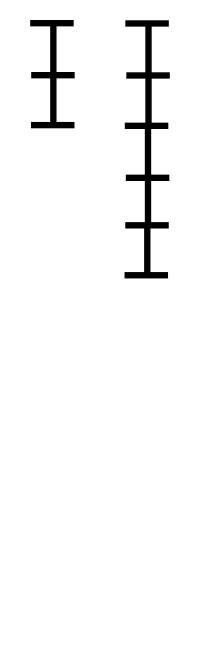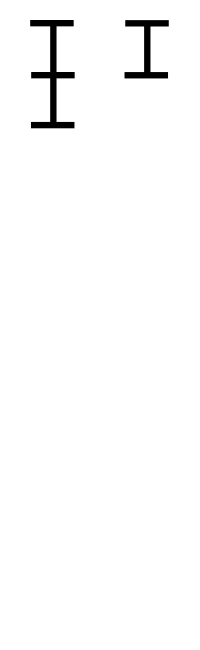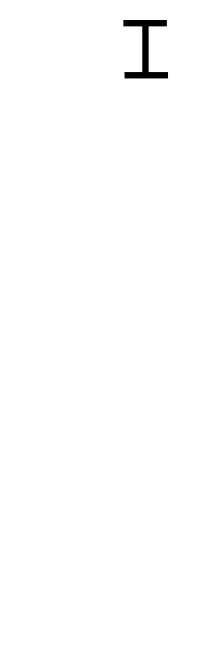
위키피디아 By Proteins - 자작, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=6639790

위 그림을 보면 어떤 구조인지 확실히 파악이 될 것이다.

3. 구현 코드

간단하게 재귀로 구현 할 수도 있고, 혹은 반복문으로 구현할 수도 있다.
아래는 c언어로 구현한 코드이다.

1) 재귀

int gcd(int a,int b){
	return b ? gcd(b, a%b) : a;
}

2) 반복문

int gcd(int a, int b)
{
    int c;
	while(b)
	{
		c = a % b;
		a = b;
		b = c;
	}
    return a;
}

※ 재귀와 반복문의 성능 분석

일반적으로는 반복문 방식이 월등히 빠르다.
이는 재귀 함수가 자기 자신을 호출할 때마다 스택 메모리에 새로운 프레임(반환 주소, 매개변수 등)을 생성하는데 반복문 방식은 변수만 갱신하여 사용하기 때문이다.
또한 재귀 방식은 스택 메모리에 새로운 프레임이 쌓이기 때문에 메모리 소모도 좀 더 큰 편이다.

참고 자료

• 유클리드 호제법 - 위키피디아
• By Proteins - 자작, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=6639790