자료의 처리
1. 우선순위 평가
(1) 인접행렬
① 개념
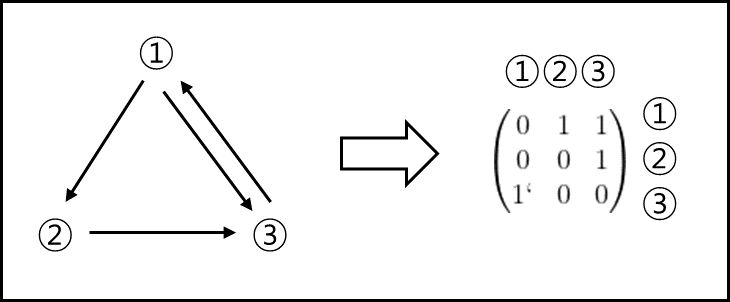
요소간의 연결 관계를 나타내는 정사각행렬
(수학적으로 엄밀한 정의는 아님)
ex)
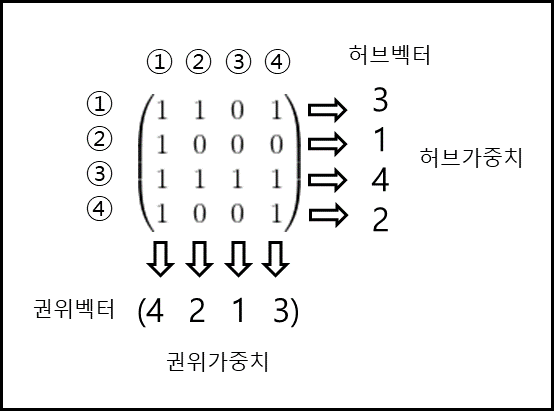
② 권위벡터와 허브벡터
$n \times n$ 인접행렬 $A=(a_{ij})$에 대하여
\(\begin{pmatrix} \sum_{i=1}^{n}a_{i1} \\ \sum_{i=1}^{n}a_{i2} \\ \vdots \\ \sum_{i=1}^{n}a_{in} \end{pmatrix}\)와 \(\begin{pmatrix} \sum_{j=1}^{n}a_{1j} \\ \sum_{j=1}^{n}a_{2j} \\ \vdots \\ \sum_{j=1}^{n}a_{nj} \end{pmatrix}\)을 각각 A의
권위벡터와 허브벡터라 하며, 각 벡터의 성분을 권위 가중치와 허브 가중치라 한다.
(2) 순위평가 원리
인접행렬 A와 초기권위벡터 $u_{0}$와 초기허브벡터 $v_{0}$에 대하여
\(u_{k}=\left\{\begin{matrix} u_{0}, k=0 \\ \frac{A^{T}v_{k}}{\left\| A^{T}v_{k} \right\|}, k>0 \end{matrix}\right.\)
\(v_{k}=\left\{\begin{matrix} v_{0}, k=0 \\ \frac{Au_{k-1}}{\left\| Au_{k-1} \right\|}, k>0 \end{matrix}\right.\)
와 같이 새로운 정규화된 권위벡터 $u_{k}$와 허브벡터 $v_{k}$를 정의한다. (k는 정수)
이때 $v_{k},u_{k}$를 연립하면 다음과 같이 정규화된 $u_{k}$와 $v_{k}$의 점화식을 얻을 수 있다.
$u_{k}=\frac{(A^{T}A)u_{k-1}}{\left| (A^{T}A)u_{k-1} \right|}$
마찬가지로 $v_{k}=\frac{(AA^{T})v_{k-1}}{\left| (AA^{T})v_{k-1} \right|}$
이 벡터들이 안정화가 되었다고 판단되는 상태로부터 각각 최종 중요도를 판별한다.
(3) 사례
10개의 인터넷 페이지들(ㄱ~ㅊ) 간의 인접행렬 A가 다음과 같다고 하자.

(2)에서 소개된 절차에 따라 A의 정규화된 권위벡터가 안정화(이전 단계의 값과 차이가 없어질때) 될때까지
반복계산한 결과는 다음과 같다.

따라서 $u_{10}$ 권위가중치로부터 페이지 ㄱ,ㅂ,ㅅ,ㅈ는 관련이 적고, 그외의
페이지는 중요도가 높은 것부터 ㅁ > ㅇ > ㄴ> ㅊ > ㄷ = ㄹ 순서대로
검색엔진에서 노출되어야함을 알 수 있다.
2. 자료압축
(1) 특잇값 분해
① 특잇값 분해
한 행렬을 여러 행렬들의 곱으로 표현하는 것.
ex) QR분해, LU분해, LDU분해, 고윳값분해, 해센버그 분해, 슈르 분해, 특잇값 분해등
② 특잇값
$m \times n$행렬 A에 대하여 $\lambda_{1},\lambda_{2},\lambda_{3},…,\lambda_{n}$이
$A^{T}A$의 고윳값일 때
\(\sigma _{1}=\sqrt{\lambda_{1}}, \sigma _{2}=\sqrt{\lambda_{2}},... \sigma _{n}=\sqrt{\lambda_{n}}\)
을 A의 특잇값이라 한다.
ex) 행렬 \(\begin{pmatrix} 1 & 1 \\ 0 & 1 \\ 1 & 0 \\ \end{pmatrix}\)에 대하여
\(A^{T}A=\begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ \end{pmatrix}\begin{matrix} 1 & 1 \\ 0 & 1 \\ 1 & 0 \\ \end{matrix}=\begin{pmatrix} 2 & 1 \\ 1 & 2 \\ \end{pmatrix}\)이므로
$AA^{T}A$의 고유방정식은 $\lambda^{2}-4\lambda+3=(\lambda-1)(\lambda-3)=0$ 이다.
따라서 A의 두 특잇값은 각각 $\sqrt{3}, 1$이다.
③ 특잇값 분해
영행렬이 아닌 임의의 $m \times n$행렬 A는
다음과 같이 나타낼 수 있다.
\(A=U\Sigma V^{T}\)
이때 U, V는 직교행렬이며, $\Sigma$는
주대각성분이 A의 특잇값이고 나머지 성분들은 0인 $m\times n$행렬이다.
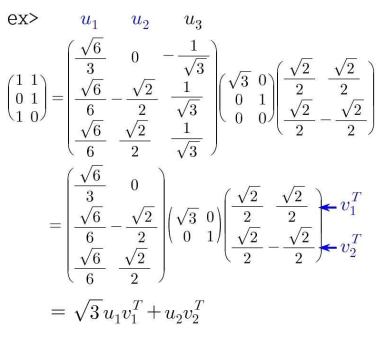
ex> 행렬 \(\begin{pmatrix} 1 & 1 \\ 0 & 1 \\ 1 & 0 \\ \end{pmatrix}\)는 다음과 같이 특잇값 분해된다.
$A=U\Sigma V^{T}$ \(\begin{pmatrix} 1 & 1 \\ 0 & 1 \\ 1 & 0 \\ \end{pmatrix}=\begin{pmatrix} \frac{\sqrt{6}}{3} & 0 & -\frac{1}{\sqrt{3}} \\ \frac{\sqrt{6}}{6} & -\frac{\sqrt{2}}{2} & \frac{1}{\sqrt{3}} \\ \frac{\sqrt{6}}{6} & \frac{\sqrt{2}}{2} & \frac{1}{\sqrt{3}} \\ \end{pmatrix}\begin{pmatrix} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \\ \end{pmatrix}\begin{pmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \end{pmatrix}\)
(2) 축소된 특잇값 분해
특잇값 분해에서 0인 성분들로만 이루어진,
대수적으로 무의미한 행 또는 열을 제거한 형태를 축소된 특잇밗 분해라 한다. 즉,
$A=U_{1}\Sigma_{1}V_{1}^{T}$ \((u_{1}u_{2},...,u_{k}) \begin{pmatrix} \sigma_{1} & 0 & 0 & 0 \\ 0 & \sigma_{2} & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & \sigma_{k} \\ \end{pmatrix}\begin{pmatrix} v_{1}^{T} \\ v_{2}^{T} \\ \vdots \\ v_{k}^{T} \end{pmatrix}\)
또한 축소된 특잇값 분해를 이용하여 행렬 A를 다음과 같이 전개한 것을 A의 축소된 특잇값 전개라 한다.
\(A=\sigma _{1}u_{1}v_{1}^{T}+\sigma_{2}u_{2}v_{2}^{T}+\cdots+\sigma_{k}u_{k}v_{k}^{T}\)
(3) 자료압축 원리
압축되지 않은 $m\times n$행렬 A를 위한 필요 저장 공간은 mn이다.
A를 축소된 특잇밗 분해한 결과가 \(A=\sigma _{1}u_{1}v_{1}^{T}+\sigma_{2}u_{2}v_{2}^{T}+\cdots+\sigma_{k}u_{k}v_{k}^{T}\)라면,
이제 필요한 저장 공간은 $k+km+kn=k(1+m+n)$이다. $\sigma_{1}\geq\sigma_{2}\geq\cdots\sigma_{k}$
충분히 작다고 판단되는 $\sigma_{r+1},\cdots,\sigma_{k}$에 대응하는 항들을 추가로 제거하면,
이때 필요한 저장공간은 $r(1+m+n)$뿐이다.