정렬 1

정렬

데이터를 사용하려면 특정한 법칙에 따라 분류가 되어있어야한다.
그리고 이런 분류 중에 가장 많이 쓰는 것은 정렬이다.
이런 정렬의 종류를 크게 두 가지로 나누자면 안정 정렬과 불 안정 정렬로 나눌 수 있다.

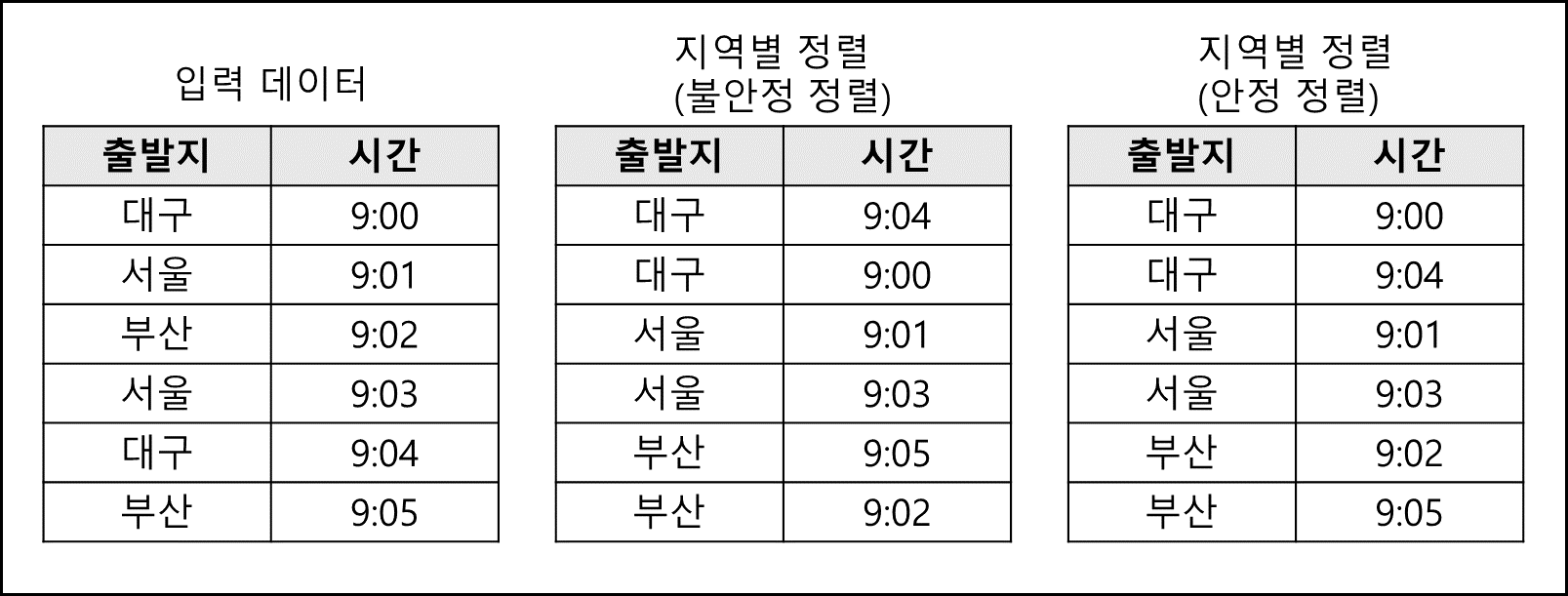
안정 정렬은 기존의 데이터 순서를 유지한채 정렬이 되는 것이고 불안정 정렬은 기존 데이터 순서와 관계 없이 정렬이 되는 것이다.

그냥 이렇게 들으면 잘 이해가 가지 않을 수 있으므로 아래의 예시를 보자.

원래 입력 데이터가 시간순서로 되어있기 때문에 안정 정렬의 경우 시간 순서가 유지된채로 출발지에 대해서만 정렬이 되지만 불안정 정렬의 경우 원래 입력 데이터의 형태인 시간 순서가 보장되지 않는다.

1. 선택 정렬 (불안정 정렬)

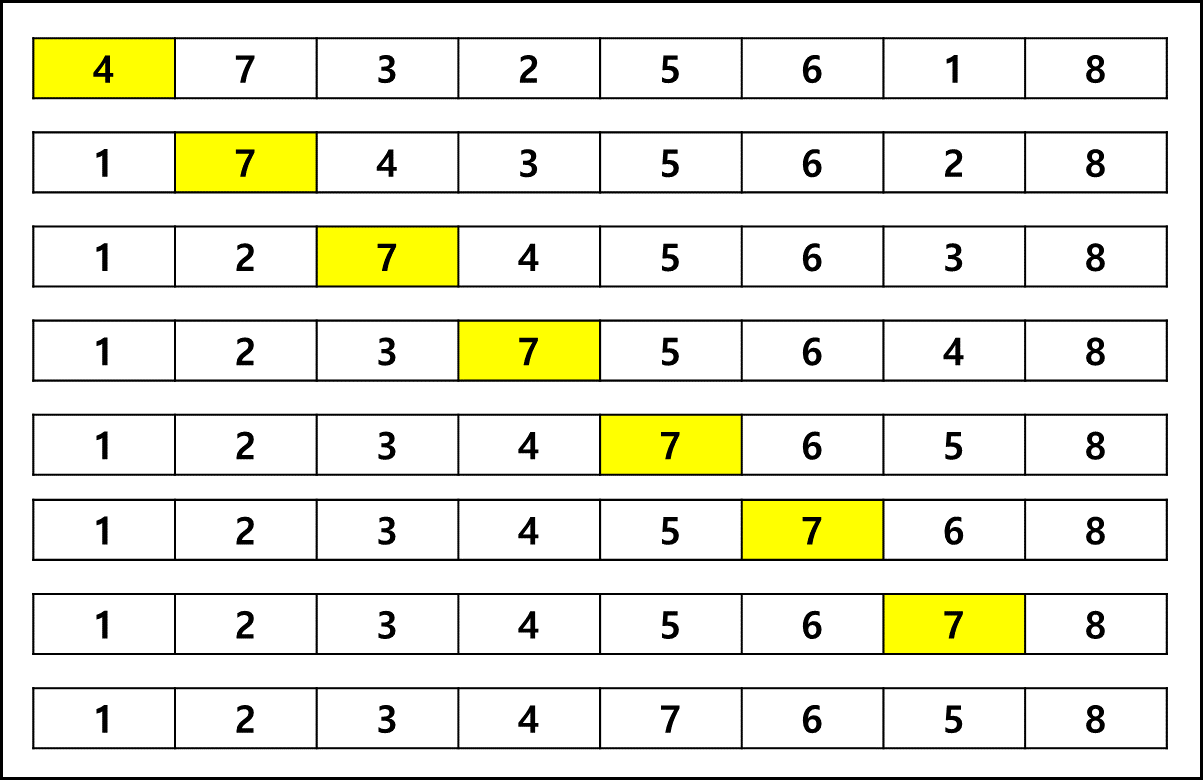
작은 순서에서 큰 순서대로 나열한다고 가정해보자 이때 현재 것 중에 가장 작은 것을 찾아 가장 왼쪽에 두고, 그 다음 작은 것을 찾아 직전에 둔 것 바로 오른쪽에 두는 식으로 끝까지 체크하면 정렬이 될 것이다. 이 선택 정렬이 그런 방법으로 정렬하는 것이다. 불안정 정렬법에 속한다.

시간 복잡도

• 최악 : $O(N^{2})$
• 평균 : $O(N^{2})$
• 최선 : $O(N^{2})$

2. 삽입 정렬 (안정 정렬)

작은 순서에서 큰 순서대로 나열한다고 가정해보자 이때 S 번째를 기준으로 자신을 포함한 왼쪽은 정렬된 것, 오른쪽은 정렬되지 않은 것을 둔다고 하고, 오른쪽 정렬되지 않은 것에서 왼쪽 정렬된 것 순서대로 데이터를 넣어가면서 정렬한다고 하면 이 S가 배열 크기 N의 N-1까지 갔을때 이 배열 전체는 모두 정렬이 될 것이다. 삽입 정렬은 이런식으로 정렬 되는 것이다. 안정 정렬법에 속한다.

※ 참고 : 이진 탐색으로 삽입

삽입 정렬을 할 때 위의 그림에서 S를 기준으로 왼쪽은 이미 정렬이 되어있다. 그렇다면 오른쪽부터 왼쪽으로 하나씩 비교하면서 원소를 밀어낼게 아니라, 이미 정렬된 왼쪽 배열에서 이진 탐색으로 위치를 찾으면 어떨까?
이런 경우 최악의 경우 N번을 모두 Search 해야하는 것보다 NlogN번 Search하면 되니 꽤나 합리적으로 보인다.
하지만 이 경우 맹점이 하나 있는데 기존 삽입 정렬의 경우 오른쪽에서 왼쪽으로 하나씩 비교하면서 원소를 한칸씩 SWAP하는 과정을 거치는데 이진 탐색으로 위치를 찾을 경우 어차피 넣어야하는 위치에서 오른쪽에 위치한 원소들을 하나씩 밀어야 하기 때문에 일반적으로는 드는 시간은 비슷하다.

일반적인 경우의 전제는 2가지이다.
비교 연산의 시간적 비용이 크지 않거나, 정렬 대상이 배열일 경우이다.

1. 원시타입 데이터는 비교하는데 시간적인 비용이 크지 않다. 하지만 객체값을 비교해야한다면? 이건 비용이 매우 커질 수 있다.
2. 정렬대상이 연결리스트 일 경우에는 어떨까? 이 경우 원소를 굳이 밀지 않아도 되고 연결 관계만 다시 연결해주면 된다.
   (물론, 연결 리스트에서 다음 원소로 넘어갈때 드는 시간적 비용이 더 크긴하다.)

시간 복잡도

• 최악 : $O(N^{2})$
• 평균 : $O(N^{2})$
• 최선 : $O(N)$

3. 쉘 정렬 (안정 정렬)

삽입 정렬은 특성상 어느정도 정렬된 데이터에 사용하면 성능이 아주 높게 나온다. 이런 부분에 착안하여 “Donald L. Shell”이라는 사람이 삽입 정렬을 보완하여 제안한 정렬방법이다.
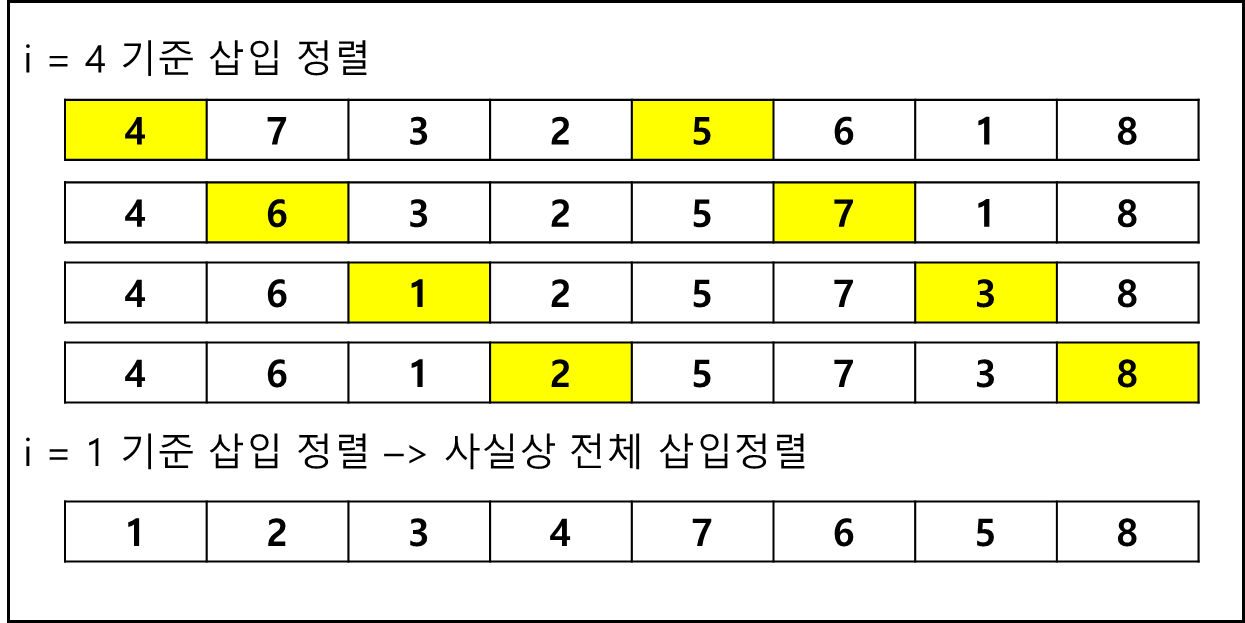
이 방법의 요체는 특정 거리 i를 두고 위치한 요소들을 부분적으로 삽입 정렬로 정렬된 배열을 만드는 것이다. 이 i를 줄여가며 삽입 정렬 방식으로 부분 정렬된 배열을 만들다가 i가 1이 되는 순간 모든 배열이 정렬되게 된다. 안정 정렬법에 속하며 초기 i값을 잡는 방법은 여러가지가 있지만 O(N^1.5)가 보장된 “i = 3 * (직전i) + 1” 수식을 사용한다. 거리가 1, 4, 13, 40, 121, 364, 1093… 순으로 늘어난다.

시간 복잡도

• 최악 : $O(N^{2})$
• 평균 : $O(N^{1.5})$
• 최선 : $O(N)$

4. 버블 정렬 (안정 정렬)

가장 느리기로 악명높은 정렬방법이다. 알고리즘은 매우 간단하다. 인접한 두 개의 요소를 비교하여 바꾸는 것이다. 이렇게 한번 순회하고 나면 오름차순 정렬의 경우 가장 큰 요소가 제일 뒤에 가 있게되고 배열 요소 개수가 N일때 N번 순회하고 나면 해당 배열이 전체 다 정렬이 되어있는 식이다.

전체를 나타내기에는 너무 많아서 한번의 순회만 나타냈다.

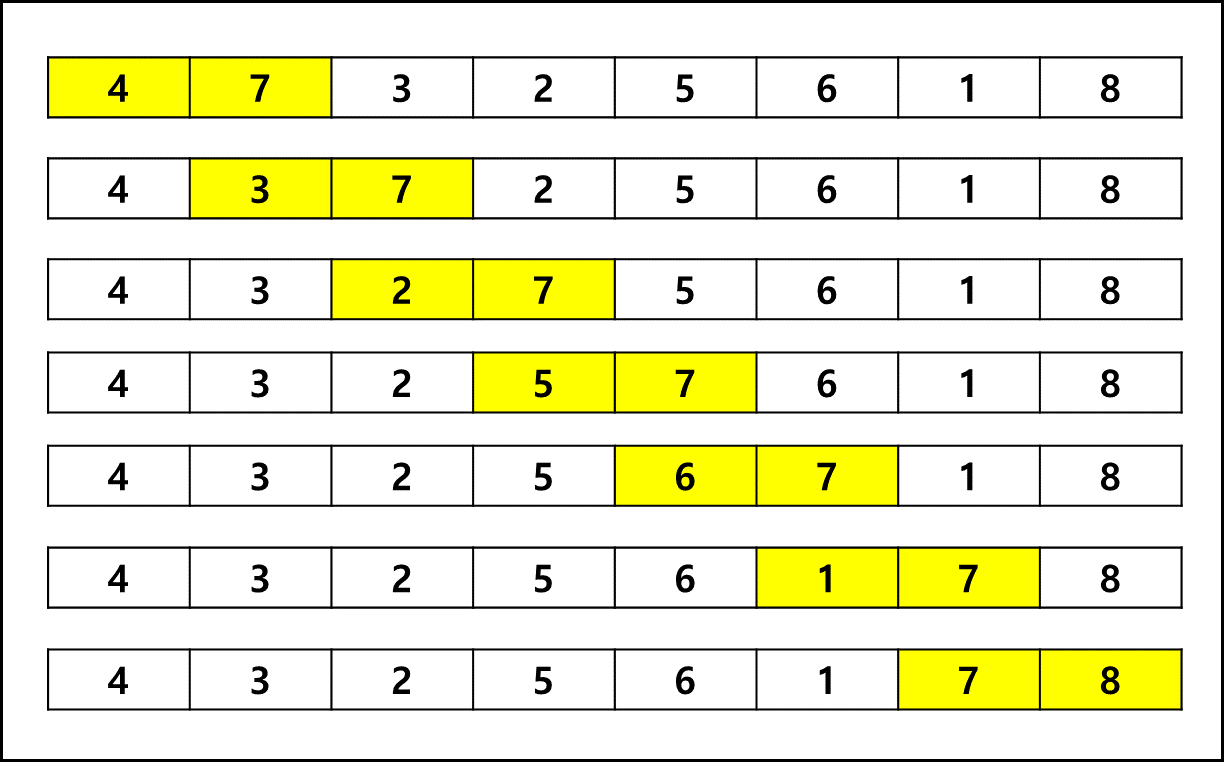
가장 큰 데이터가 오른쪽 끝으로 밀려난걸 볼 수 있다. 나머지 N-2번만 더 순회하면 완전히 정렬할 수 있다.

시간 복잡도

• 최악 : $O(N^{2})$
• 평균 : $O(N^{2})$
• 최선 : $O(N^{2})$

참고 자료

• R.Sedgewick and K. Wayne, Algorithms (4th Ed.), Addioson-Wesley.
• E. Horowitz, S. Sahni, S. Anderson-Freed, Fundamentals of Data Structures in C, Silicon Press, 2nd Edition.
• Stranger’s lab : 자바 [JAVA] - 이진 삽입 정렬 (Binary Insertion Sort