정렬 2
퀵 정렬 (불안정 정렬)
이론상 가장 빠른 정렬이다. 그래서 이름이 퀵 정렬이라고 붙었다.
하나의 리스트를 피벗 기준으로 작고 큰 것으로 나누어 정렬 한다.
pviot을 어떻게 선정하느냐에 따라서 이 알고리즘의 속도 차이가 매우 커진다.
- 분할(Divide): 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열로 분할한다.
- 정복(Conquer): 분할된 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
- 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다. 순환 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.
| 4 | 7 | 3 | 2 | 5 | 6 | 1 | 8 |
위와 같은 임의의 배열 A가 있을 때 아래는 A를 오름차순으로 퀵 정렬한 순서를 나타낸 것이다.

무작위의 값을 pivot으로 두고 왼쪽 비교대상을 l, 오른쪽 비교대상을 r이라 했을때
- r은 왼쪽으로 l은 오른쪽으로 움직인다. r이 pivot보다 작고, l이 pivot보다 큰 데이터를 가리키면 둘을 swap한 뒤 동일한 조건을 찾는다.
- 이동하다가 r과 l이 만나게되면 pivot과 swap한다.
- pivot과 swap한 시점을 기준으로 배열을 좌 우로 나눠서 둘다 1~2 절차를 수행한다.
- 재귀적으로 수행하여 배열 크기가 1로 내려가면 정렬이 완료 된 것이다.
시간 복잡도를 살펴보자.
최선의 경우 정렬 대상 배열의 크기가 2의 제곱승 형태이고 pivot은 매번 대상 배열 값들 중 중앙값이다. 그런 경우 최대 순환호출의 경우 logN이 된다. 여기에 비교 연산 N을 곱하면 시간 복잡도는 O(NlogN)이 된다.
최악의 경우는 이미 정렬된 데이터를 다시 정렬할 경우이다. pivot을 통해 나눌때마다 n-1개와 1개의 배열로 나눠질때 최대 N번 순환 호출하게되고 비교 연산은 N번이니 시간 복잡도는 O(N^2)이다.
시간 복잡도
- 최악 : $O(N^{2})$
- 평균 : $O(Nlog_{2}N)$
- 최선 : $O(Nlog_{2}N)$
병합 정렬 (안정 정렬)
병합 정렬도 퀵 정렬과 마찬가지로 분할 정복 알고리즘이다. 가장 작은 배열 단위로 나눠서 나눈 배열끼리 합쳐가는 것으로 최선의 경우에도 최악의 경우에도 항상 일정한 성능을 보인다.
종류는 크게 상향식 정렬(Bottom-up merge sort)와 하향식 정렬(Top-down merge sort) 두 가지가 있다.
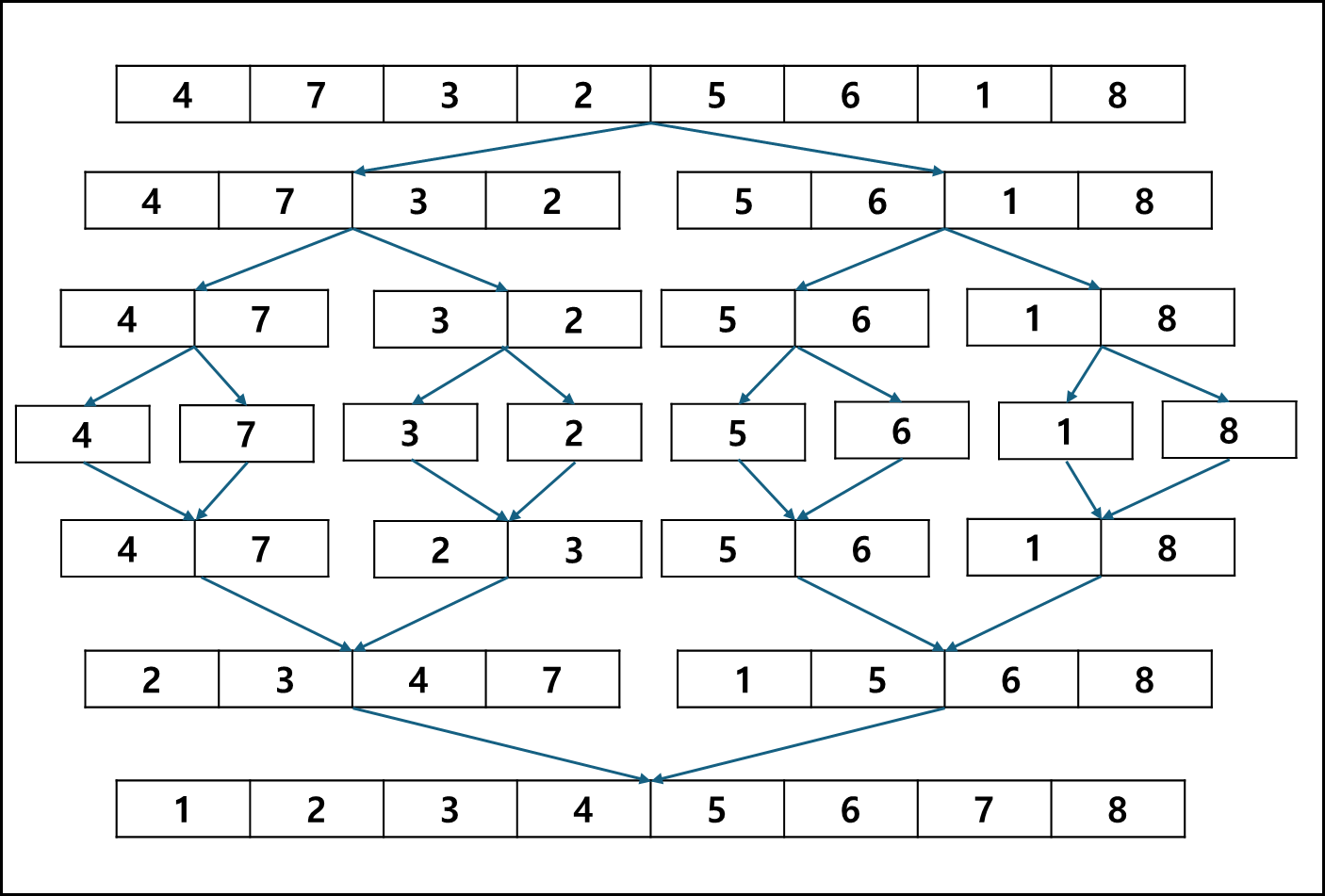
Top-down merge sort
배열을 절반씩 쪼개서 가장 작은 단위가 될 때까지 쪼갠뒤 쪼개둔 배열들을 차례대로 합치는 방법이다.
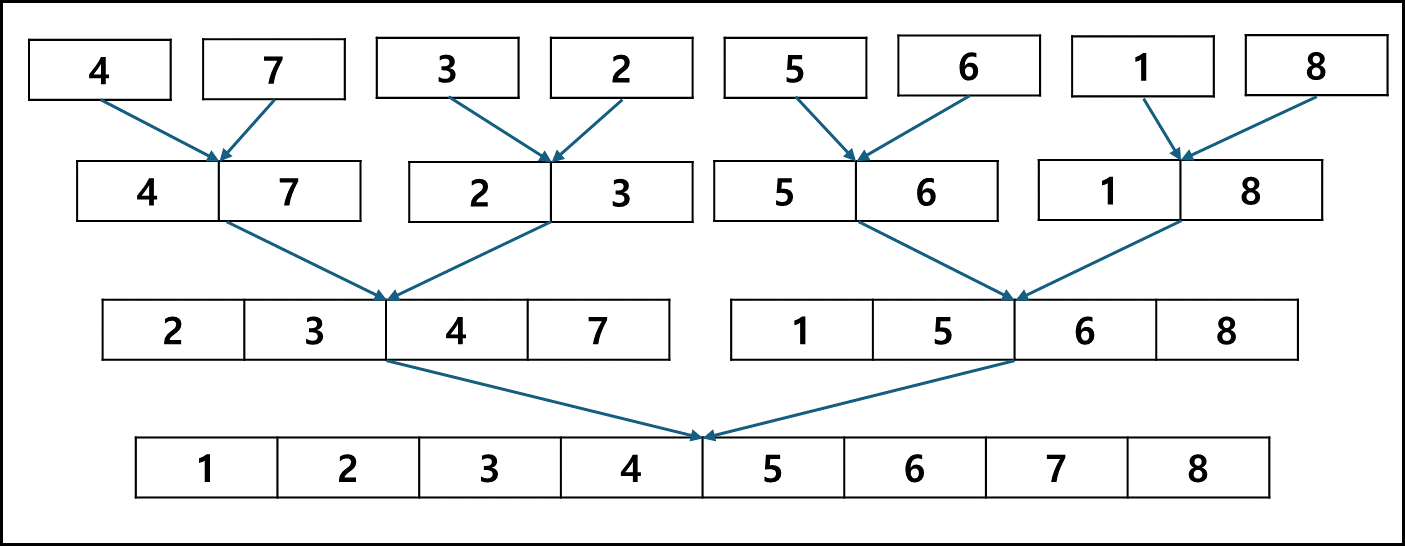
Bottom-up merge sort
단일 요소들을 작은 배열로 보고 2개씩 짝으로 합쳐가며 정렬하는 방법이다.
시간 복잡도를 계산해보자. 최선이든 최악이든 이 병합정렬은 성능이 일정하게 나온다. 모든 경우에서 절반씩 잘라서 병합해가며 문제를 해결하므로 logN이 된다 이러한 하나의 병합 단계에서 최대 비교하는 연산이 N번 이루어지므로 시간 복잡도는 O(NlogN)이 되게 된다.
항상 $Nlog_{2}N$이면 완전 최고의 알고리즘 아닌가?하는 생각이 들수있겠지만 이 병합 정렬의 가장 큰 단점은 정렬하고자하는 배열만큼의 추가 메모리가 필요하다는 부분이다. 이런 부분을 여러가지 트릭으로 줄이고, 삽입 정렬을 추가하여 시간 성능과 메모리 성능을 극도로 올린 알고리즘이 바로 팀 정렬이다.
이러한 팀 정렬에 대해서는 다음 링크를 참고하라.
시간 복잡도
- 최악 : $O(Nlog_{2}N)$
- 평균 : $O(Nlog_{2}N)$
- 최선 : $O(Nlog_{2}N)$
참고 자료
- https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html
- R.Sedgewick and K. Wayne, Algorithms (4th Ed.), Addioson-Wesley.
- E. Horowitz, S. Sahni, S. Anderson-Freed, Fundamentals of Data Structures in C, Silicon Press, 2nd Edition.