정렬 3
계수 정렬 - Counting Sort (안정 정렬)
키 값이 0을 포함한 양의 정수일때만 사용 가능한 정렬법이다. 각각 요소인 양의 정수값을 인덱스로 사용하여 해당 배열을 정렬하는 방법이다. 입력 배열 A와 그의 길이 N, 임시배열 T와 T의 길이 K, 출력배열을 R이라고 할때 순서는 다음과 같다.
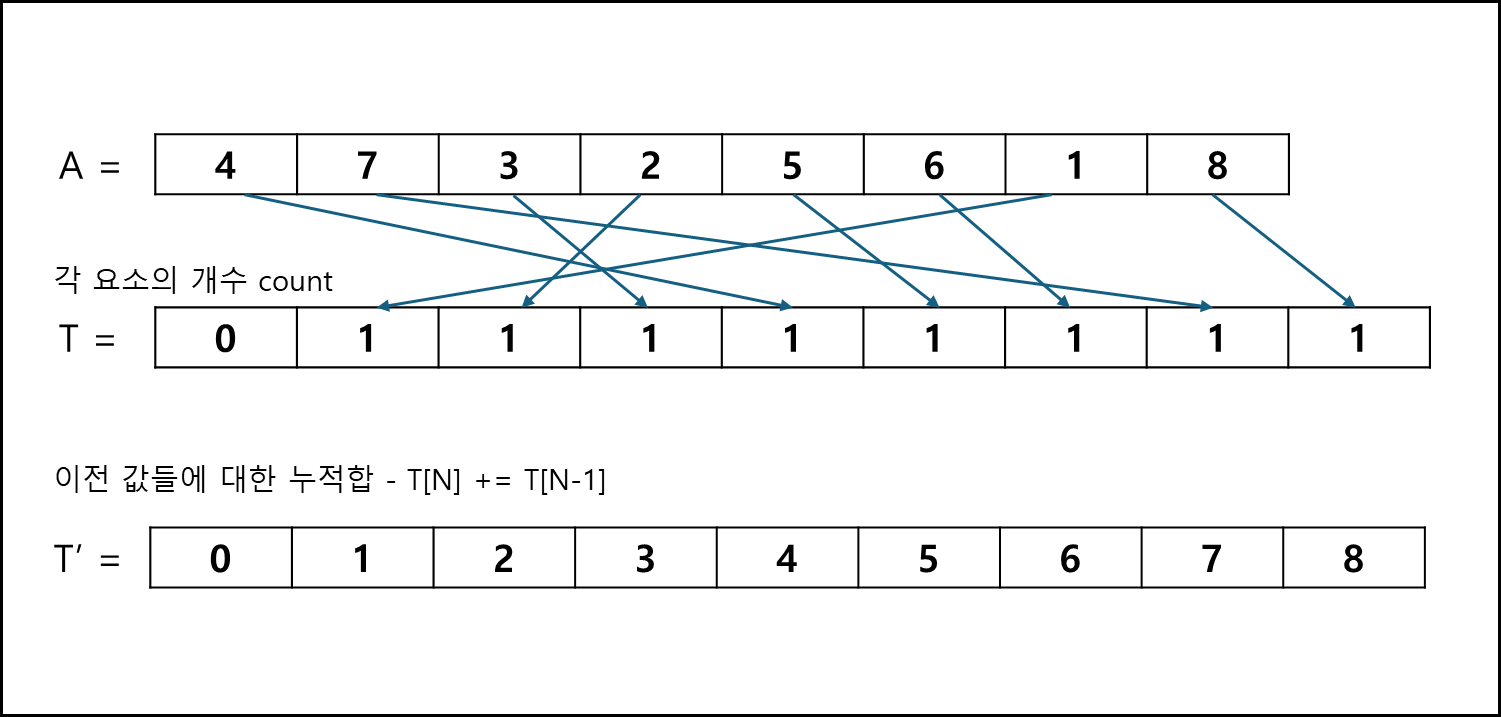
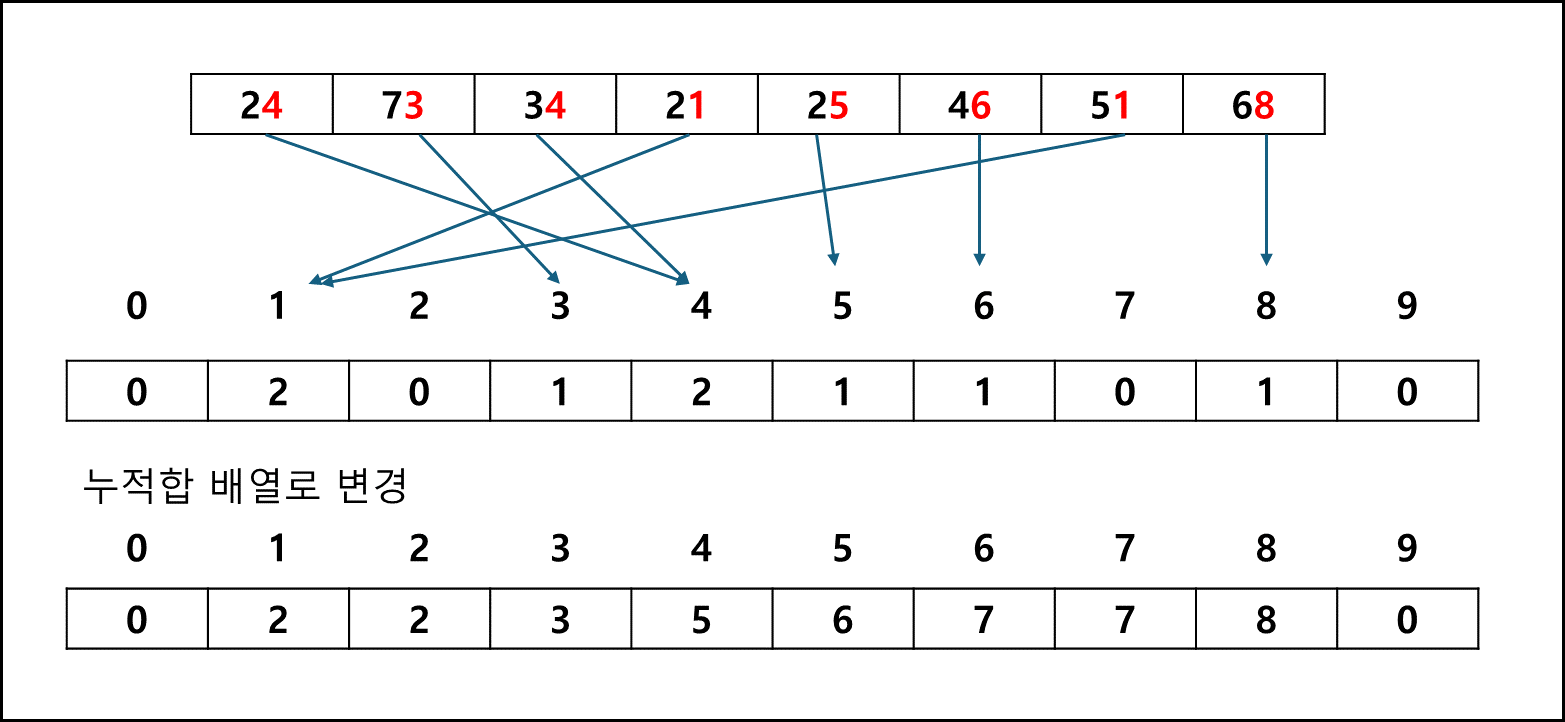
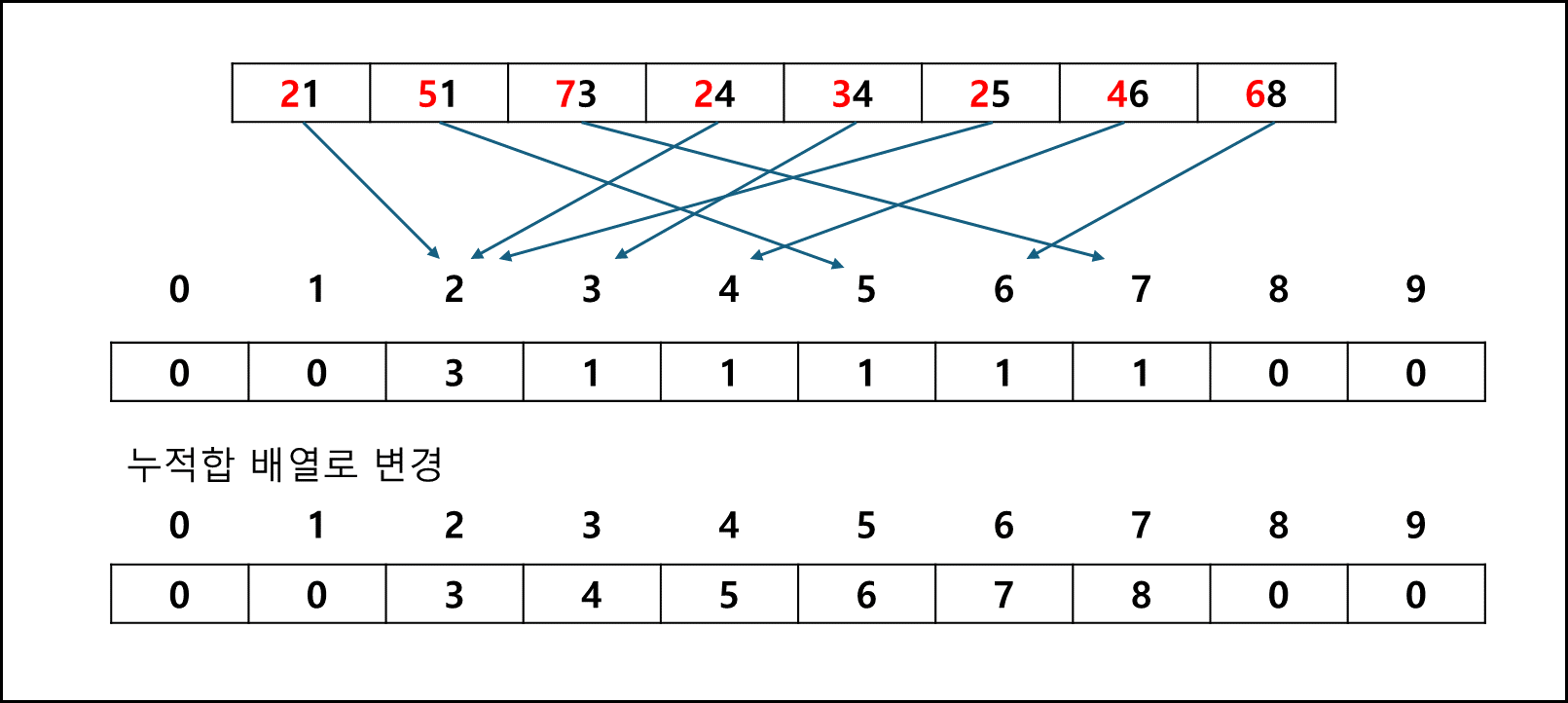
입력배열 A 전체를 순회하며 각각 나오는 값 i에 대해서 T[i] += 1로 개수를 세어준다.
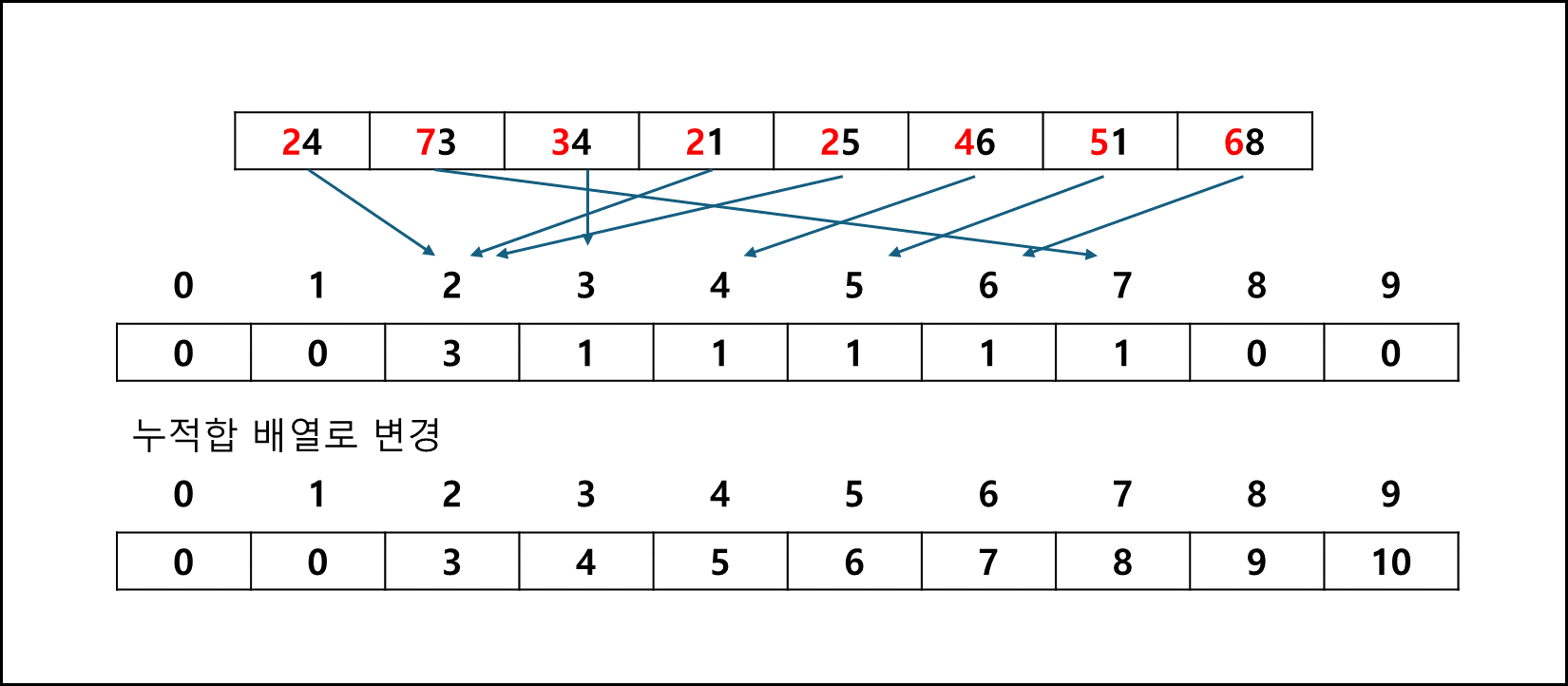
ex) A = 1,1,2,3,4 일 경우, T = 0,2,1,1,1T 배열의 값을 누적합으로 만들어준다.
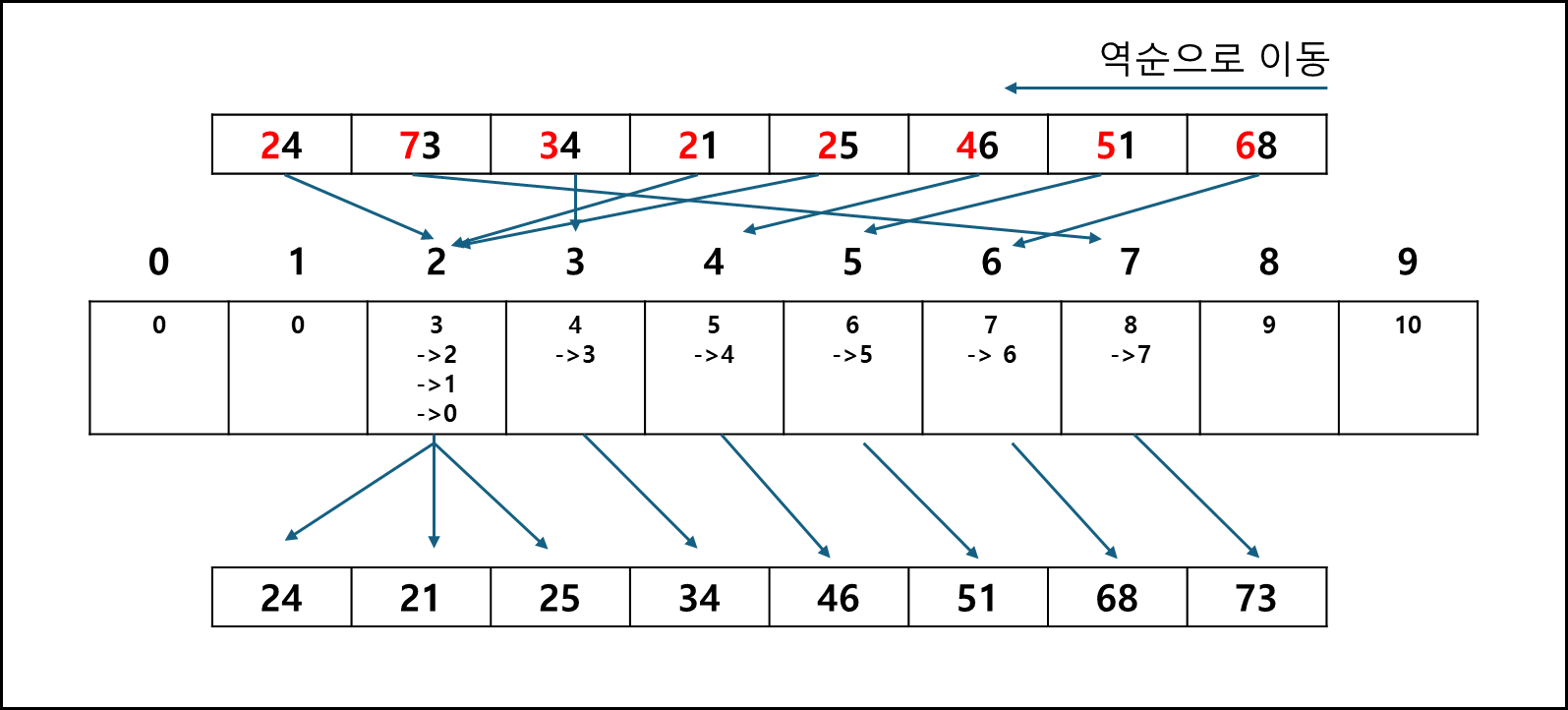
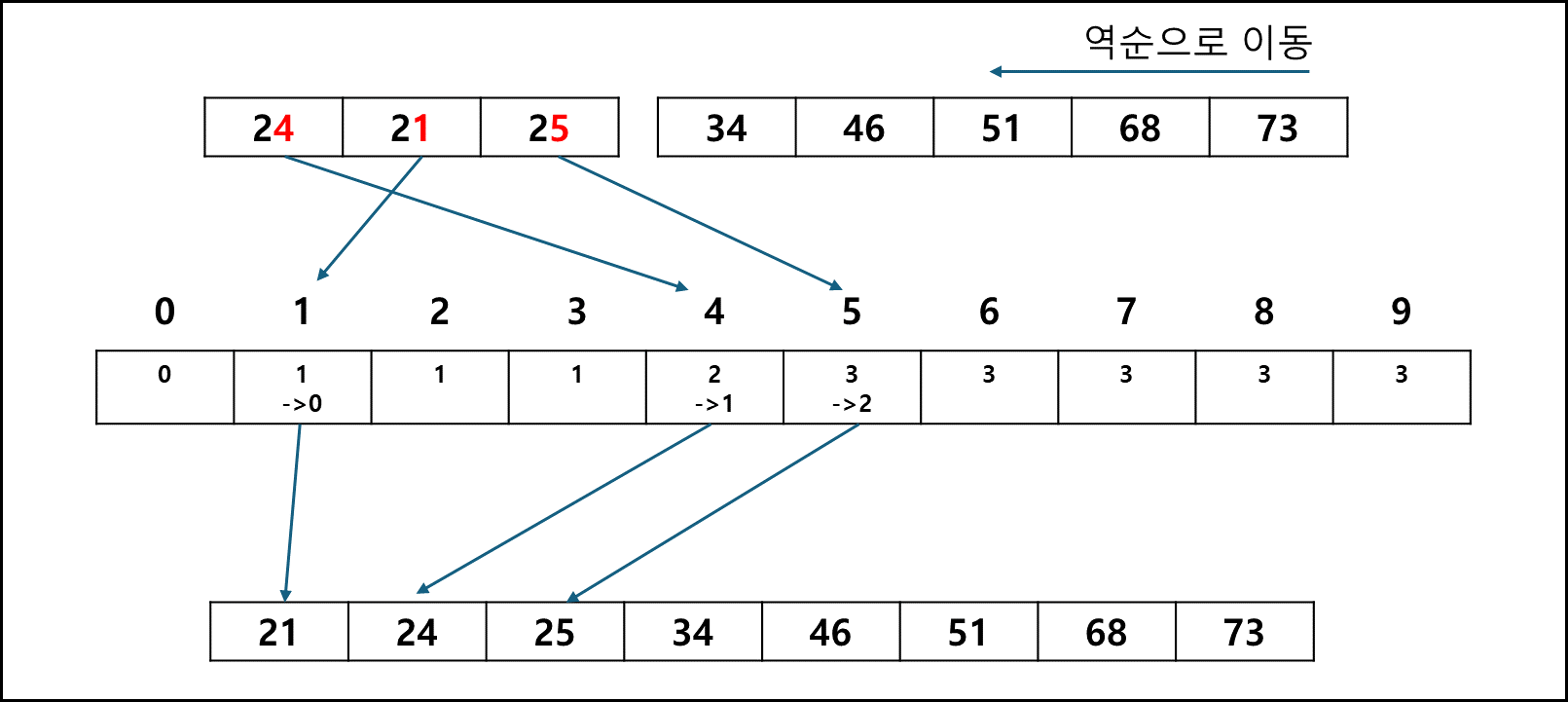
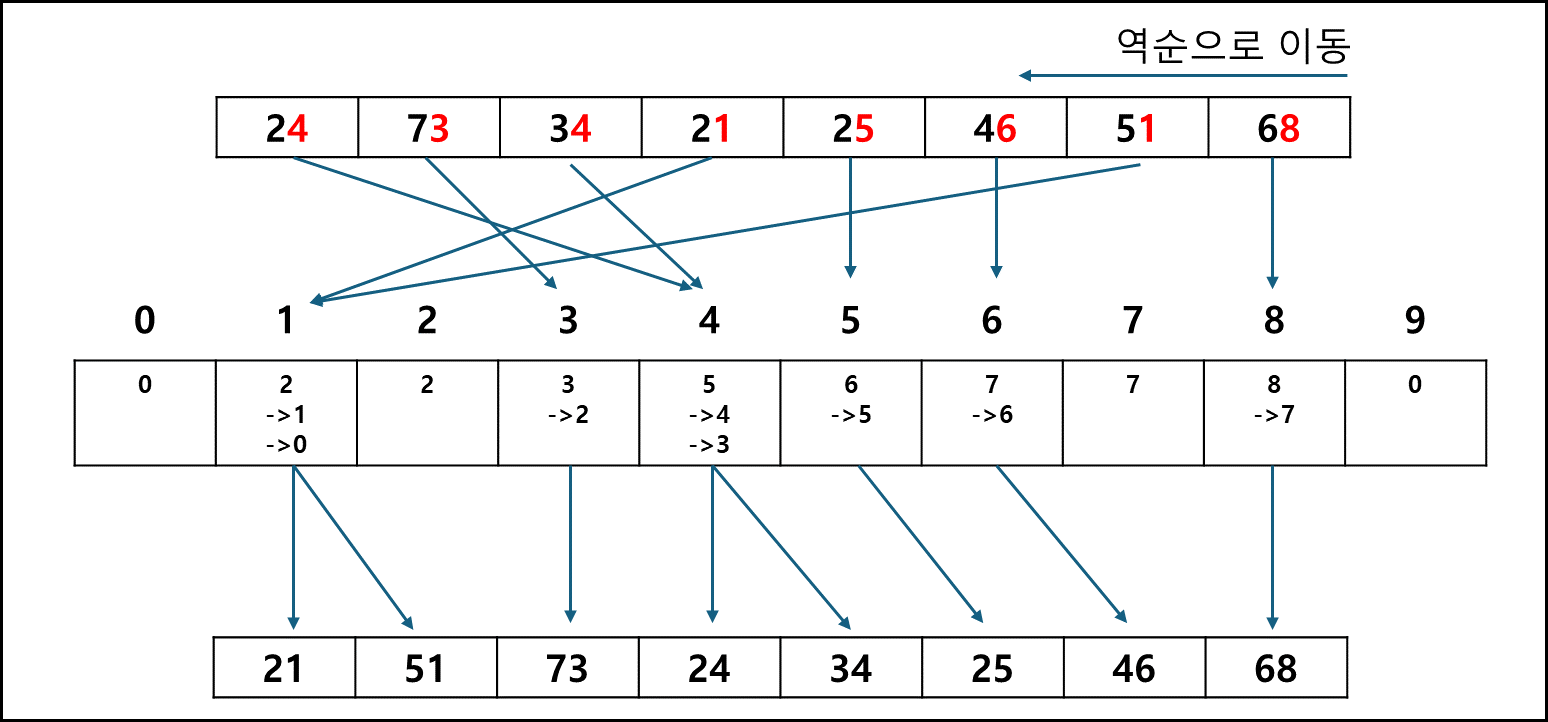
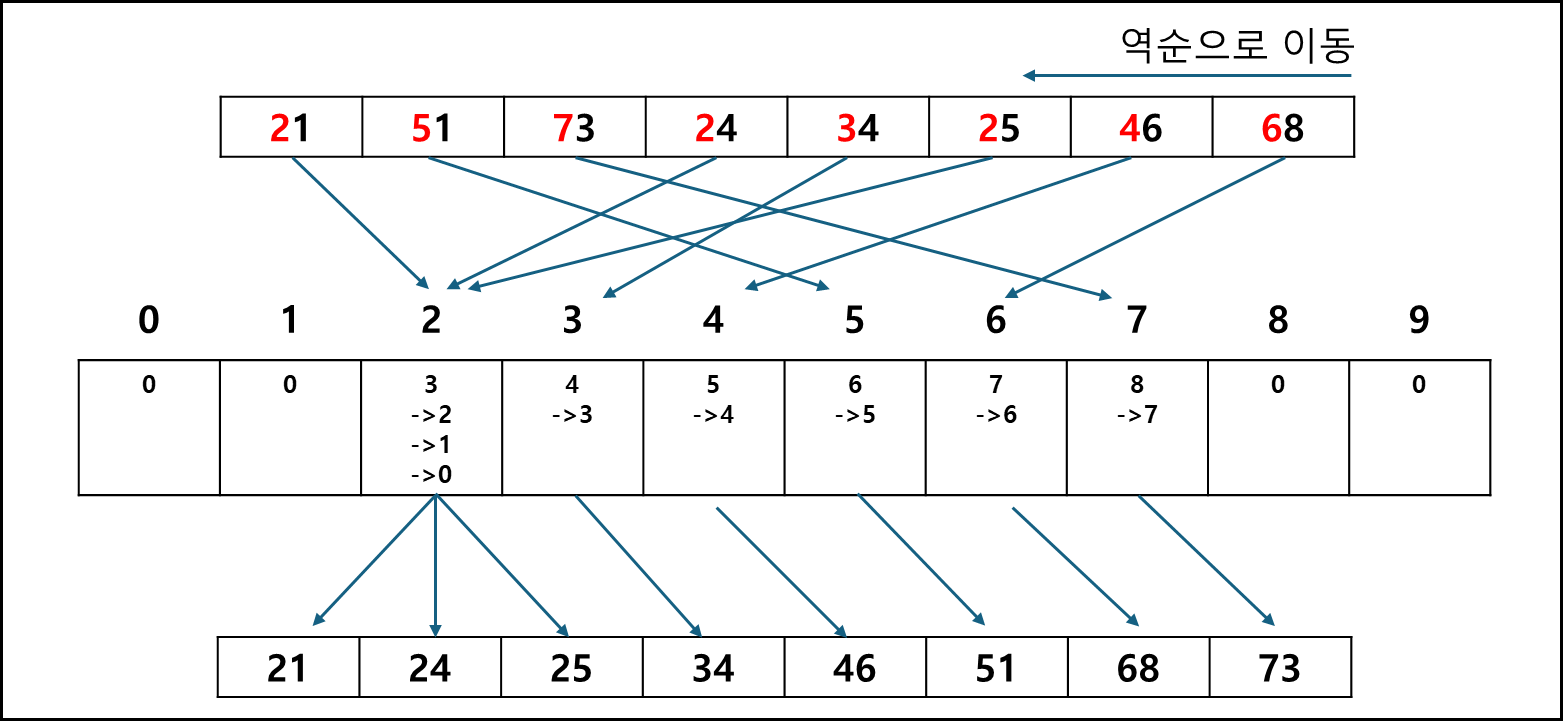
ex) 원래 T = 0,2,1,1,1 => 누적합 처리한 T’ = 0,2,3,4,5이후 입력배열 A의 값을 역순으로 순회하여 T’값을 -1하여 index로 사용하여 R배열에 출력한다.
이렇게 글로 들어선 제대로 이해가 가지 않을테니 예를 들어 보겠다.
첫번째 값 이동만 표기했는데 N-1 이후로도 값의 이동은 위의 그림과 같다.
시간 복잡도
기본적으로 이 알고리즘의 시간 복잡도는 $O(N+K)$, 공간 복잡도는 $O(N+K)$이다 이 정렬은 N이 K와 비슷하다면 $O(N)$수준으로 빠르나, K가 N의 세제곱이라면 시간 복잡도도 $O(N^{3})$수준으로 느려진다.
버킷 정렬 - Bucket Sort (경우에 따라 다름)
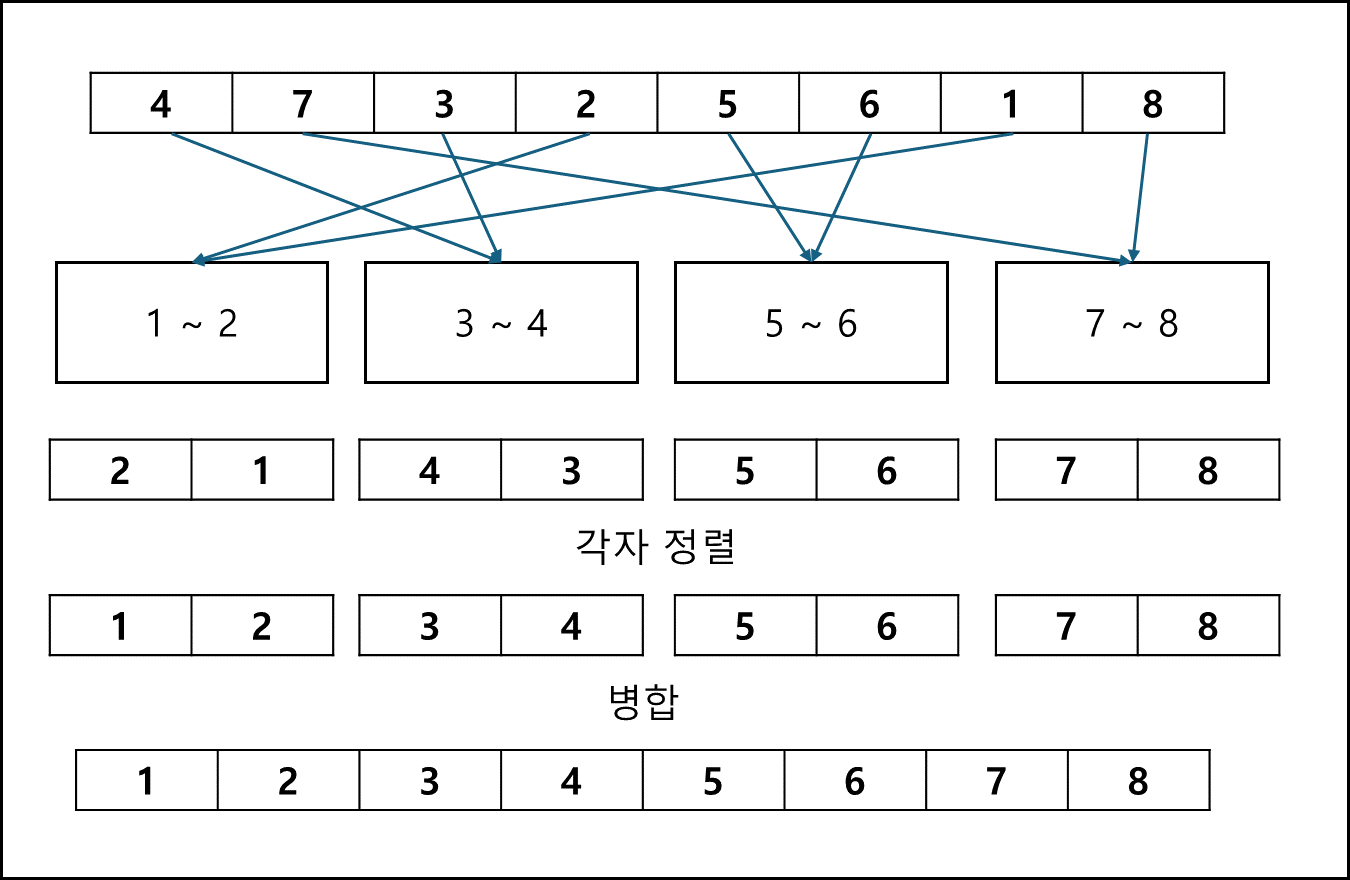
계수 정렬에서 각 요소를 index로 쓴 것은 어떻게보면 각 요소를 담는 크기를 1개로 지정한 것과 같다. 이 크기를 1개가 아닌 1개 초과의 크기로 두게 되면 버킷 정렬과 같다.
가령 1~30까지의 숫자가 무작위로 배열되어있는 배열 A가 있다고 가정해보자
이 경우 숫자 5개까지 끊어서 넣는 버킷 (1~5,6~10등) 6개가 있다고 할 때 각 버킷은 숫자가 5개씩 들어가게 된다. 이후 버킷안에서 무작위로 들어가 있는 값을 버킷 내에서 각각 정렬시킨뒤 각 버킷의 순서대로 합쳐주고 정렬된 배열이 나오게 된다.
이때 각각의 버킷을 정렬할시에 다른 정렬 알고리즘을 사용하게 되는데 이때 안정 정렬 알고리즘을 사용하면 버킷 정렬 역시 안정 정렬이 된다.
시간 복잡도
- 최악 : $O(N+K)$ : K는 버킷 갯수
- 평균 : $O(N+K)$
- 최선 : $O(N^{2})$
기수 정렬 - Radix Sort (경우에 따라 다름)
어떻게보면 bucket 정렬과 같다. 하지만 자릿수를 기준으로 정렬한다는 점이 다르다. 두 가지 정렬 방식이 있다. 가장 큰 것을 먼저 선택하는 MSD 방식과 가장 작은 것을 먼저 선택하는 LSD 방식이다.
MSD
높은 자리수 부터 정렬하는 방법을 MSD라고 한다.
MSD의 경우 각 높은 자리수 별로 먼저 정렬을 하는데 각 자리수 별로 또 정렬을 해주어야한다.
먼저 10의 자리 별로 sort를 해준다.
10의 자리 순서대로 sort할시에 다음과 같이 된다.
이제 1의 자리 순서대로 sort를 할 것인데 문제는 10의 자리 별 sort한 것끼리 sort를 해서 각 자리 순으로 더해서 배열을 생성해야한다는 점이다.
다음의 그림을 보자
20의 자리는 별도로 정렬을 해주고, 뒤의 다른 자리는 순서대로 붙이면 된다.
LSD
낮은 자리수 부터 정렬하는 방법은 LSD이다.
LSD는 MSD와는 다르게 각 자리수 별로 정렬을 해줄 필요가 없어서 많이 쓴다.
먼저 1의 자리수 부터 정렬을 해준다.
1의 자리수를 정렬했으면 이제 10의 자리수로 정렬해주면 되는데 MSD와는 달리 별도의 분리 없이 그냥 바로 다시 정렬하면 된다.
기수정렬은 안정정렬? 불안정 정렬?
LSD의 경우 일반적으로 안정 정렬이나 MSD의 경우 일부 구현 방식에 따라 불안정 정렬이 되므로 주의해서 사용해야한다.
시간 복잡도
- 최악 : $O(NK)$ : K는 최대 자리수
- 평균 : $O(NK)$
- 최선 : $O(NK)$
참고 자료
- 위키백과 - 버킷 정렬
- 위키백과 - 기수 정렬
- stresszero.log - 정렬 알고리즈 개념 정리
- R.Sedgewick and K. Wayne, Algorithms (4th Ed.), Addioson-Wesley.
- E. Horowitz, S. Sahni, S. Anderson-Freed, Fundamentals of Data Structures in C, Silicon Press, 2nd Edition.