집합의 순서
부분순서집합
(1) 정의
① 부분순서관계 (Partial Order Relation)
반사적, 반대칭적, 추이적인 관계
ex 1) 두 집합 A,B에 대하여 $ A \subseteq B$
반사적 : $A \subseteq A$
반대칭적 : $A \subseteq B \wedge B \subseteq A => A = B$
추이적 : $A \subseteq B \wedge B \subseteq C => A \subseteq C$
ex 2) 두 실수 x,y에 대하여 $ x \leq y $
반사적 : x $\leq$ x
반대칭적 : $x \leq y \wedge y \leq x => x = y$
추이적 : $x \leq y \wedge y \leq z => x \leq z$
ex 3) 두 자연수 n,m에 대하여 n이 m의 배수인 관계
반사적 : 2는 2의 배수
반대칭적 : a가 b의 배수이면서 b가 a의 배수면 a = b
추이적 : 4는 2의 배수 $\wedge$ 8은 4의 배수 => 8은 2의 배수
② 부분순서집합
집합 A 상에 부분순서관계 $\leq $가 주어진 경우 A를 부분순서집합이라하고, 이를 (A, $\leq $)로 나타내기도한다.
※ 모든 원소들이 순서관계를 가져야하는 것은 아니다.
ex) A = {$\varnothing$, {1},{2},{1,2} }
(A, $\leq$)
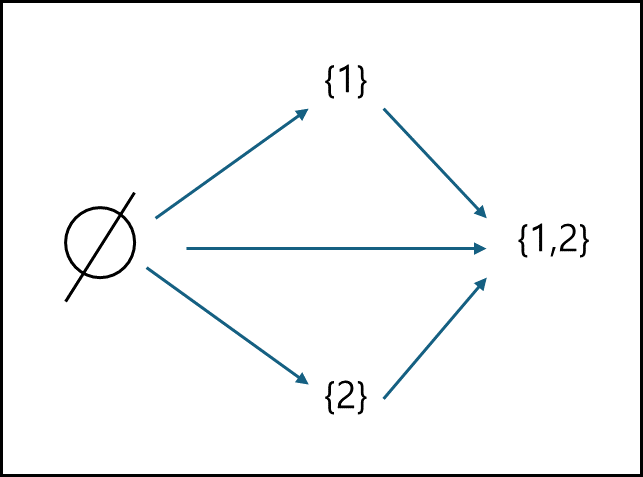
이 경우 {1}과 {2} 사이에는 순서관계를 가지지 않는다.
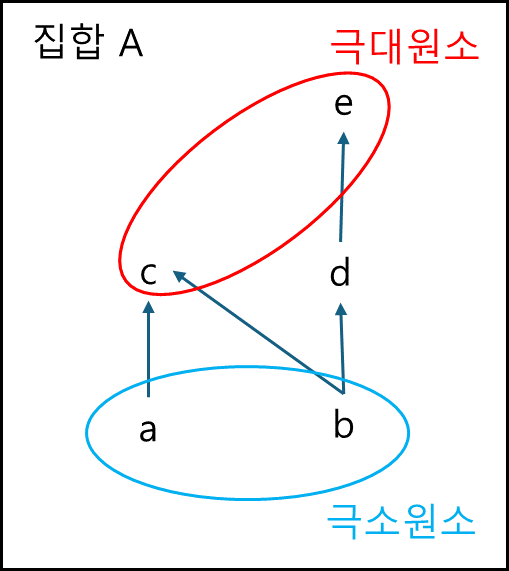
③ 극대원소와 극소원소
A가 부분순서집합이라 할 때
$\forall x \in A, x \geq a \Rightarrow x = a$
를 만족하는 A의 원소 a를 극대원소,
$\forall x \in A, x \leq b \Rightarrow x = b$
를 만족하는 A의 원소 b를 극소원소라 한다.
이러한 극대(극소)원소는 유일하지 않을 수 있다.
ex) A의 관계가 아래와 같을 때 극대(극소)원소
ex) 멱집합 P(X)에서 $\varnothing , X$
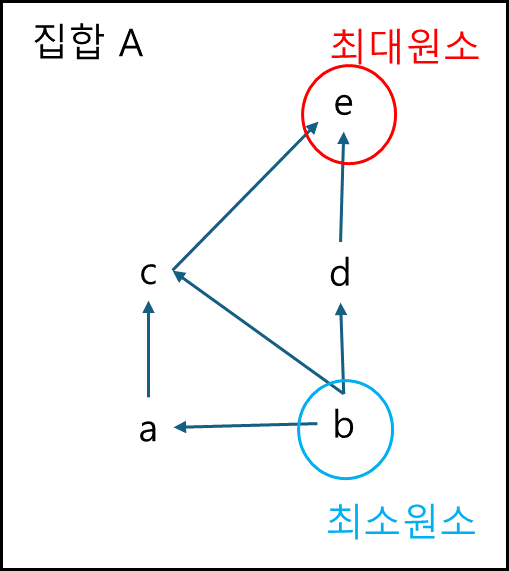
④ 최대원소와 최소원소
A가 부분순서집합이라 할 때
$\forall x \in A, x \leq a$
를 만족하는 A의 원소 a를 최대원소,
$\forall x \in A, x \geq b$
를 만족하는 A의 원소 b를 최소원소라 한다.
이러한 최대(최소)원소는 유일하거나 없다.
ex) A의 관계가 아래와 같을 때 최대(최소)원소
(2) 상한과 하한
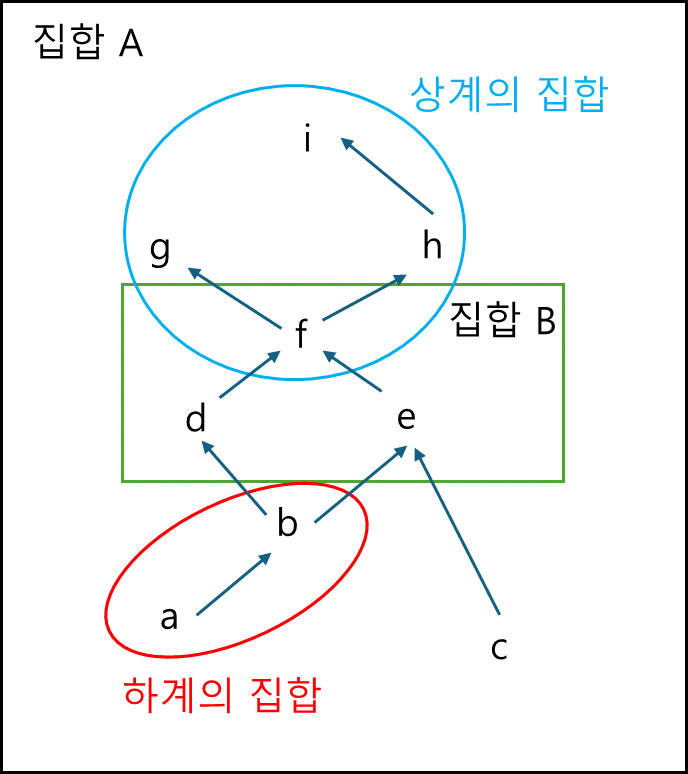
① 상계와 하계
B가 부분순서집합 A의 부분집합이라 할 때
$\forall x \in B, x \leq a$
인 $a\in A$를 A에서 B의 상계,
$\forall x \in B, x \geq b$
인 $b\in A$를 A에서 B의 하계라 한다.
ex) A와 B의 관계가 아래와 같을 때 상계와 하계
※ 하계와 상계는 여러개 일수 있기 때문에 하계와 상게의 집합이라고 표현했음
② 상한과 하한
부분순서집합 A의 부분집합 B에 대하여 B의 상계(하계)들이
집합이 최소(최대)원소를 가질때 이 원소를 A에서 B의 상한(하한)이라
하고, sup B(inf B)로 나타낸다.
ex) A = [0, 1) $\subset R$에서 0,1
(3) 절편과 절단
① 절편
부분 순서 집합 A의 원소 a에 대하여
\(S_{0} = \left\{ x \in A | x < a \right\}\)
ex1) R의 절편 \(S_{0} = \left ( -\infty , 0 \right )\)
ex2) N의 절편 \(S_{3} = \left\{ 1,2 \right\}\)
② 절단 (Cut)
1) $B \cap C = \varnothing , B \cup C = A$
2) $x \in B \wedge y \leq x \Rightarrow y \in B$
3) $x \in C \wedge x \leq y \Rightarrow y \in C$
을 만족하는 부분순서집합 A의 공집합이 아닌 부분집합들의 쌍 (B, C)
ex) R의 두 부분집합 $M = (-\infty, 0)$,
$N = [0, \infty)$에 대하여 (M,N)
ex) A가 아래와 같을때
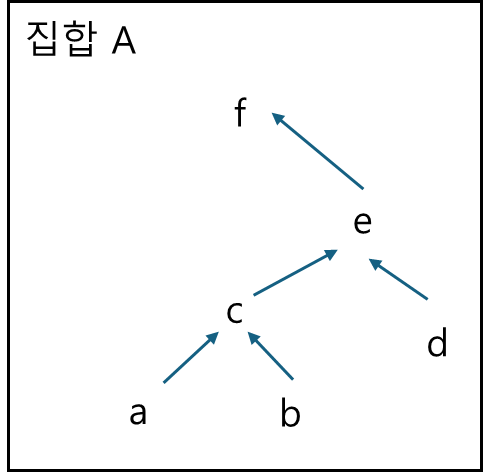
{a,b,c}와 {d,e,f}는 절단이다.
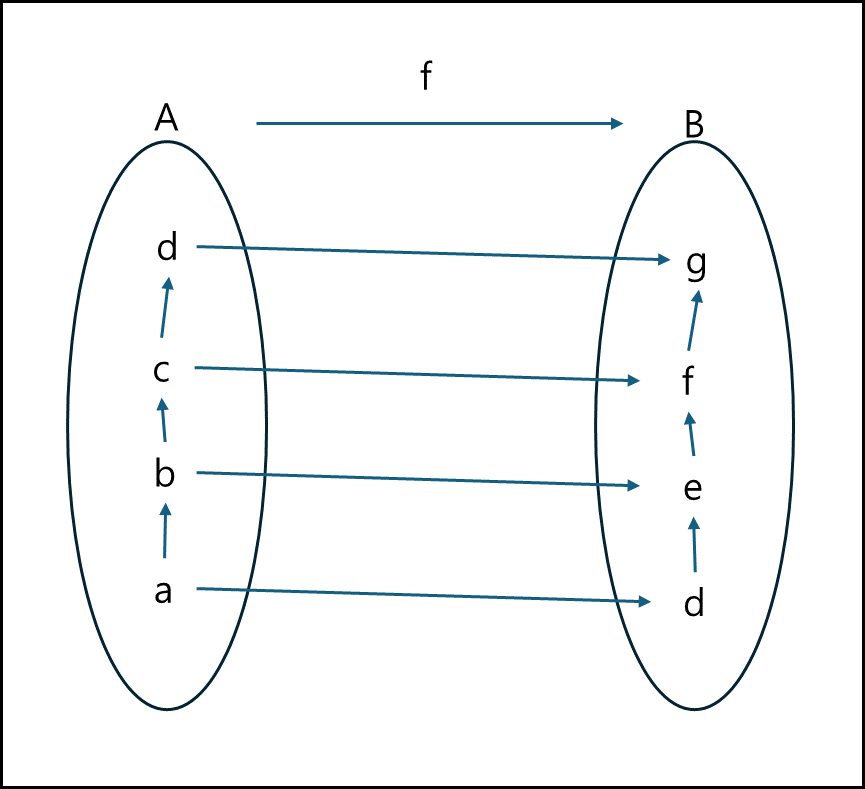
(4) 순서동형
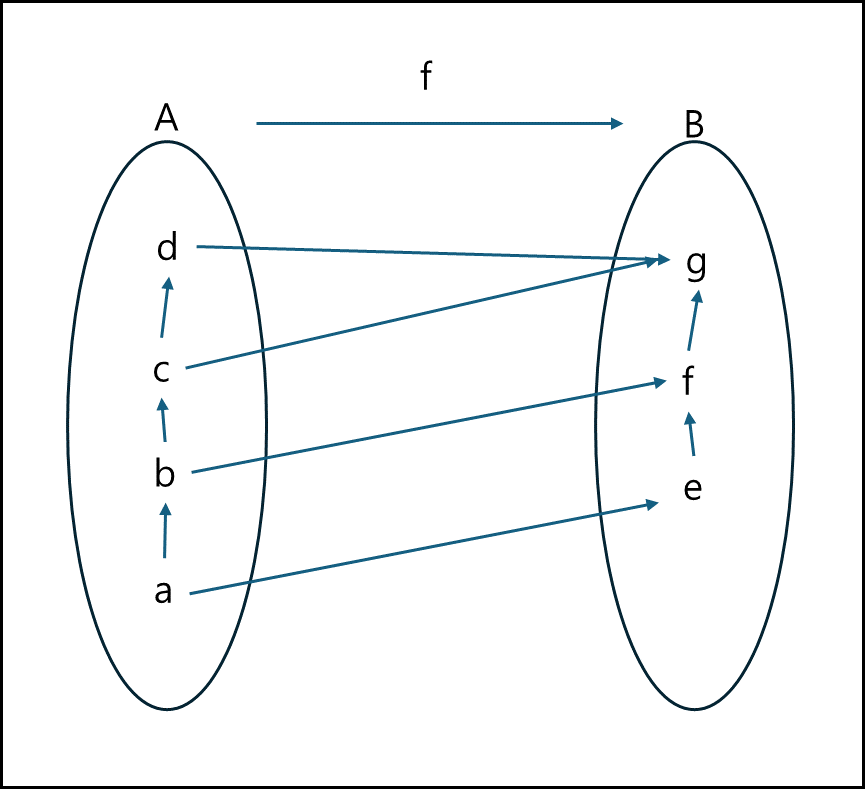
① 순서보존함수
부분 순서 집합 A,B에 대하여 함수
f : A -> B가 조건
$\forall x, y \in A, x \leq y \Rightarrow f(x) \leq f(y)$ 을 만족하면 f를 순서보존함수라 한다.
② 순서동형
부분 순서 집합 A,B에 대하여 함수
f : A -> B가 전단사이고
$\forall x, y \in A, x \leq y \Rightarrow f(x) \leq f(y)$
이면 f를 순서동형사상이라 한다.
이때 A와 B는 순서동형이라 하고 $A \simeq B$로 나타낸다.
ex) 항등함수 $I_{A} : A \to A$
2. 전순서집합
(1) 전순서집합
① 비교가능
부분순서집합 A의 두 원소 x,y가
$x \leq y \vee y \leq x$ 이면 x와 y는 비교 가능하다고 한다.
② 전순서 집합
부분 순서집합 A의 임의의 두 원소가 비교가능하다면 A를 전순서집합이라고 한다.
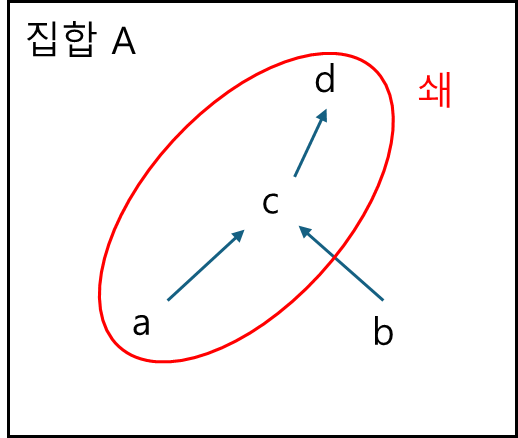
(2) 쇄 (Chain)
부분순서집합의 A의 전순서 부분집합 B를 A에서의 쇄라고 한다.
(3) 정렬집합 (Well ordered set)
부분순서집합 A의 공집합이 아닌 모든 부분집합 B가 최소원소를 가지면
그리고 그때에만 집합 A를 정렬집합이라 한다.
3. 서수
(1) 서수의 개념
① 서수
집합의 길이를 나타내는 수이다. 간단히 말해
집합안에 구조가 있을때 집합의 크기는 서수고
집합안에 구조가 없을때 집합의 크기는 기수이다.
1) 모든 정렬집합 A에 대하여 서수가 존재하며, 모든 순서수 $\alpha $에 대하여 o(A) = $\alpha $인 정렬집합 A가 존재한다.
2) $ A \approx B \Leftrightarrow o(A) = o(B)$
3) $ A = \varnothing \Leftrightarrow o(A) = 0$
4) \(A \approx \left\{ 1,2, \cdots, k \right\} \Leftrightarrow o(A) = k\)
② 유한 서수, 초한 서수
유한 서수 : 유한정렬집합의 서수
초한 서수 : 무한정렬집합의 서수
※ 대표적인 초한 서수
$\omega = o(\mathbb{N})$
자연수집합의 서수
(2) 서수의 순서
정렬집합 A,B에 대하여 $o(A) = \alpha, o(B)=\beta$일때
A가 B의 절편과 순서동형이면 $\alpha$는 $\beta$보다 작거나 같다고하면
$\alpha \preceq \beta$로 나타내고 이때 특히 $\alpha \neq \beta$이면 $\alpha \prec \beta$로 나타낸다.
ex) \(A = \left\{ 1 \right\}, B = \left\{ 3,4,5 \right\}\) 일때
$o(A) = 1 \prec o(B) = 3$
(3) 서수의 연산
① 서수 합
서로소 인 두 집합 A, B의 서수를 각각 $\alpha, \beta$라고 할때
$\alpha + \beta = o(A \cup B)$
ex) A = {1}, B={a,b} -> $B_{1}=$ {2,3} (순서 동형)
o(A) = 1, o(B)=o($B_{1}$)=2
o($A\cup B$) = o($A\cup B_{1}$) = o({1,2,3}) = 3
② 서수 곱
집합 A, B의 서수를 각각 $\alpha, \beta$라고 할때
$\alpha\beta = o(B \times A)$
ex) A = {1,2}, B={a,b,c} o(BXA) = o({(a,1),(a,2),(b,1),(b,2),(c,1),(c,2)}) = 6
③ 연산 법칙
임의의 서수 $\alpha, \beta, \gamma$에 대하여 다음이 성립한다.
1) 결합 법칙
\(\left ( \alpha + \beta \right ) + \gamma = \alpha + \left ( \beta + \gamma \right )\)
$\alpha\left ( \beta\gamma \right ) = \left ( \alpha\beta \right ) \gamma$
2) 분배 법칙
$\alpha\left ( \beta + \gamma \right ) = \alpha\beta + \alpha\gamma$
주의!) $\left ( \alpha + \beta \right )\gamma \neq \alpha\gamma + \beta\gamma$
우 분배 법칙은 적용하지 않는다.
ex) (w+1)·2 $\neq$ w·2+2
(w+1)·2 = (w+1)+(w+1)
= w+(1+w)+1
= w+(1+w)+1
= w+w+1
= w·2+1
※ 일반적으로 서수는 합과 곱에 대하여 교환 법칙이 성립하지 않는다.
합 교환 반례
1+w = w+1의 경우
1+w => {a,1,2,3 …} = w
w+1 => {1,2,3,…a}
끝이 정해진 것과 정해지지 않은 것은 차이가 있음곱 교환 반례
2·w < w·2
2·w = o(N x {0,1}) = o({(1,0),(1,1),(2,0),(2,1)…})
w·2 = o({0,1} x N) = o({(0,1),(0,2)….,(1,1),(1,2)…..})
2·w는 한 개의 무한인 반면에, w·2는 최소 두 개의 무한이다.