컴파일러 - 어휘분석기 - 유한 상태 오토마타
어휘분석기 - 유한 상태 오토마타
공부해보니 오토마타에 대한 내용은 매우 크고, 언어학과 다른 지식 어딘가에 모호하게 걸쳐있는 느낌이 있어서 다른 분류로 분리해야겠지만, 일단은 현재 컴파일러에 대해서 논하고 있으므로 일단 이곳에 포스팅하기로 했다.
1. 유한 상태 기계
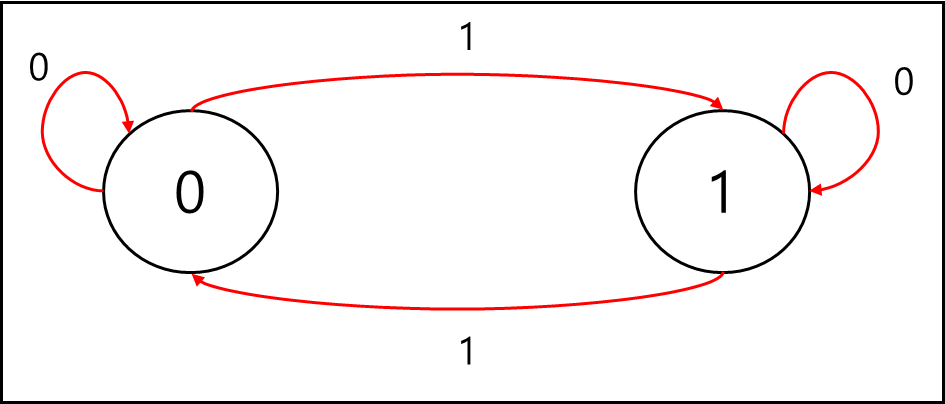
유한 상태 기계라는게 있다. 이는 상태가 유한한 기계를 말한다. 여기서 말하는 기계라는건 개념적인 기계를 말하며 아래의 그림과 같은 상태 전이도로 표현할 수 있다.
위 그림은 흔히들 아는 플립플롭(filp-flop)의 상태 전이도이다. 위와 같이 유한한 상태를 가진 것을 말하며 이러한 유한 상태 기계는 시스템을 모델링할 때 많이 사용하는 방법이다.
이러한 유한 상태 기계도 유형이 여러가지가 있으나 흔히들 보는 것은 출력이 있는 유한 상태 기계와 출력이 없는 유한 상태 기계이다.
출력이 있는 유한 상태 기계의 경우에는 출력이 상태의 추이 함수에 의해 결정되거나 출력이 상태에 의해 결정되는데 간단히 예를 들자면 자판기와 같이 어떤 입력값에 의해 상태와 반환값이 있는 것을 이야기할 수 있다.
자판기가 300원짜리 음료 한 개만 판매하고, 넣을 수 있는 동전이 100원, 500원이라고 한다면 아래와 같이 정의 할 수 있다.
입력: {100, 500, 음료뽑기}
상태: {S0, S1, S2, S3}
출력: {none, 100, 200, 300, 400, 500, 음료}
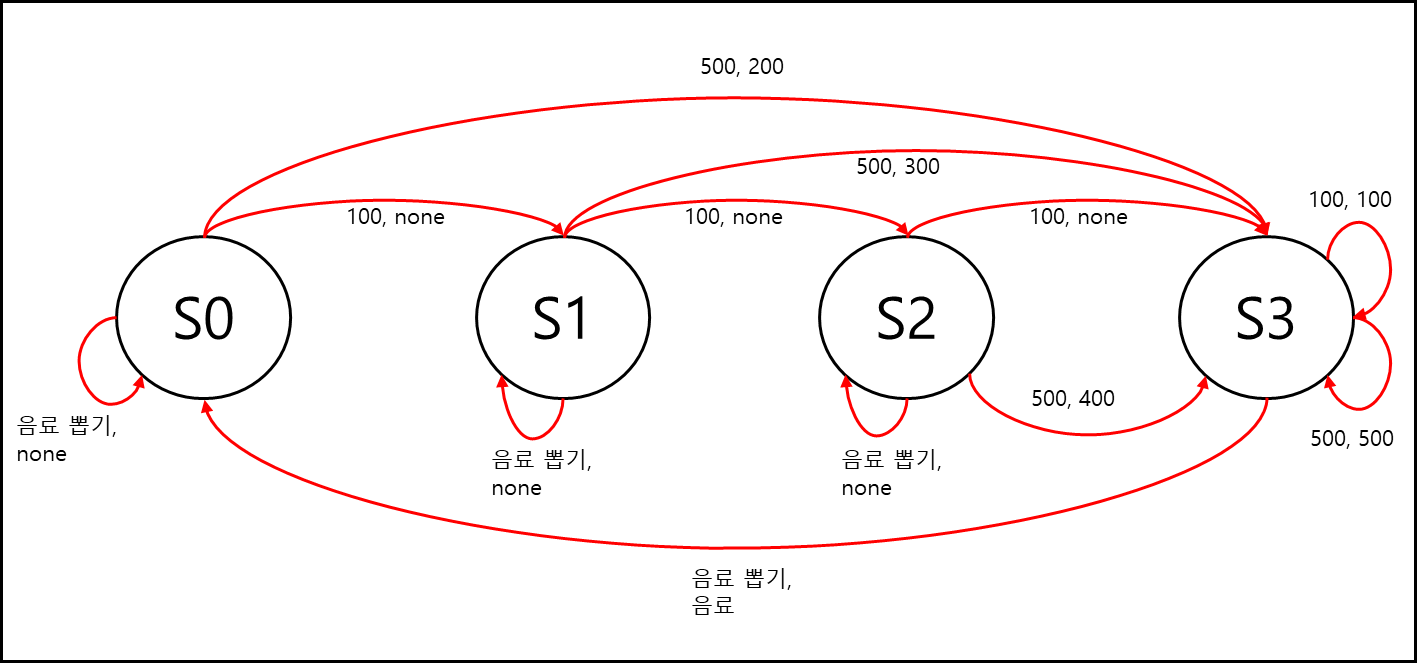
여기서 none은 아무일도 일어나지 않는것을 말한다. 위 정의 사항에 따라서 상태 전이도를 그려보면 아래와 같이 그려진다.
보면 알겠지만, 각 state를 연결하는 edge들에 {입력, 출력} 순으로 달려있다.
동전의 경우 총합이 500원 이전까지 출력은 none이지만, 500원 이상이 되는 경우 거스름돈을 출력으로 반환하며, 음료 뽑기 입력에 대해서는 500 이전까지는 none이고 총합이 500원일 경우(이상일 경우 거스름돈으로 반환하므로) 음료를 반환한다.
위와 같이 입력과 출력이 있는 경우는 출력이 있는 유한 상태 기계라고 말한다.
하지만 어휘분석기에서 사용하는 기계는 출력이 없는 유한 상태 기계, 즉 유한 상태 오토마타를 말한다.
2. 출력이 없는 유한 상태 기계(유한 상태 오토마타, Finite state Automata)
기본적으로 유한 상태 오토마타 M은 아래와 같이 나타낼 수 있다.
\[M = (S, I, f, s_{0}, F)\]S: 유한한 상태 집합
I: 유한한 입력 알파벳의 집합
f: 상태 추이 함수
$s_{0}$ : 초기 상태(starting states)
F: 최종상태(acceptance states)의 집합
상태 추이 함수라고 하면 여러가지로 표현할수 있겠지만 일단은 보기 편하게 예시를 통해 도표로 표시해보도록 하겠다.
M={S,I,f, $s_{o}$ ,F} 일때
S={$s_{0},s_{1},s_{2}$}, I={0,1}, F={ $s_{2}$ } 라고 하고 상태 추이 도표가 아래와 같다고 했을 때
| Input | ||
| 상태 | 0 | 1 |
| s0 | s0 | s1 |
| s1 | s1 | s2 |
| s2 | s1 | s0 |
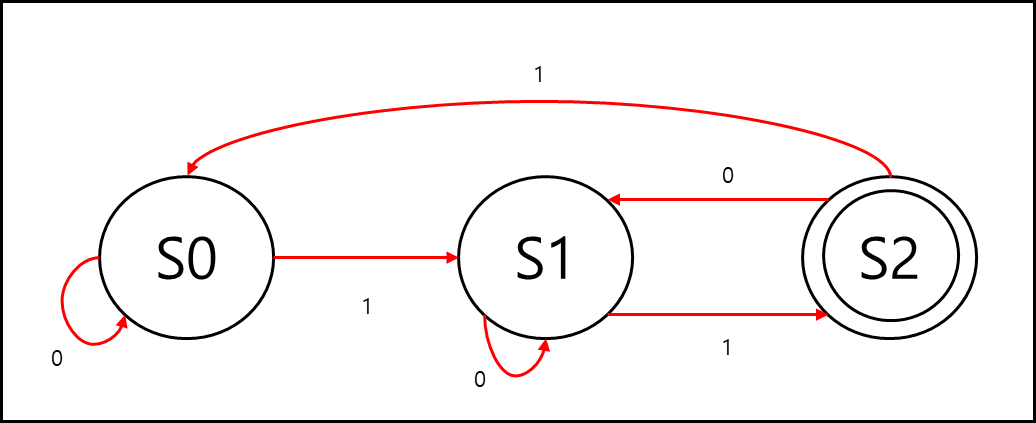
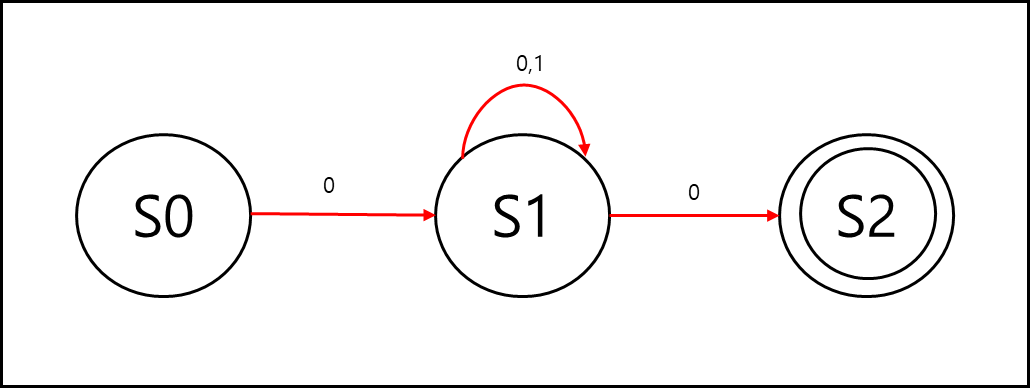
이를 유한 상태 오토마타로 표현하면 아래와 같다.
$s_{2}$의 경우 동그라미 두 개가 겹쳐진 형태인데, 이는 최종 상태 집합의 원소이기 때문에 위와 같이 표기된 것이다.
어떤 연속된 입력값에 의해 최종 결과가 최종 상태 집합의 원소 중 하나인 상태라면 이를 승인 혹은 인식되었다고 말한다.
이는 입력값의 집합이 문자열이라도 동일하며, 유한 상태 오토마타 M에 의해 승인 되는 문자열의 집합을 언어 L(M)이라고 한다.
3. NFA(Nondeterministic Finite state Automata) vs DFA(Deterministic Finite state Automata)
앞서 설명했던 그래프를 그냥 유한 상태 오토마타라고 퉁쳤는데, 사실 종류가 총 두 개이다.
크게는 비결정 유한 상태 오토마타와 결정 유한 상태 오토마타이다.
예를 들어보자 1에서 시작하여 0으로 끝나는 문자열의 L(M)이라고 하고 I={0,1}인 경우 결정 유한 상태 오토마타는 아래와 같이 표현 가능하다.
모든 입력에 대해서 상태 전이가 되고 정확하게 결정되는것을 볼 수 있다. 위와 같은 형태를 결정 유한 상태 오토마타라고 한다.
그럼 비결정 유한 상태 오토마타는 무엇인가? 어떤 입력값에 대해서 상태전이가 다수 존재할 수 있으며 입력 값에 대해서
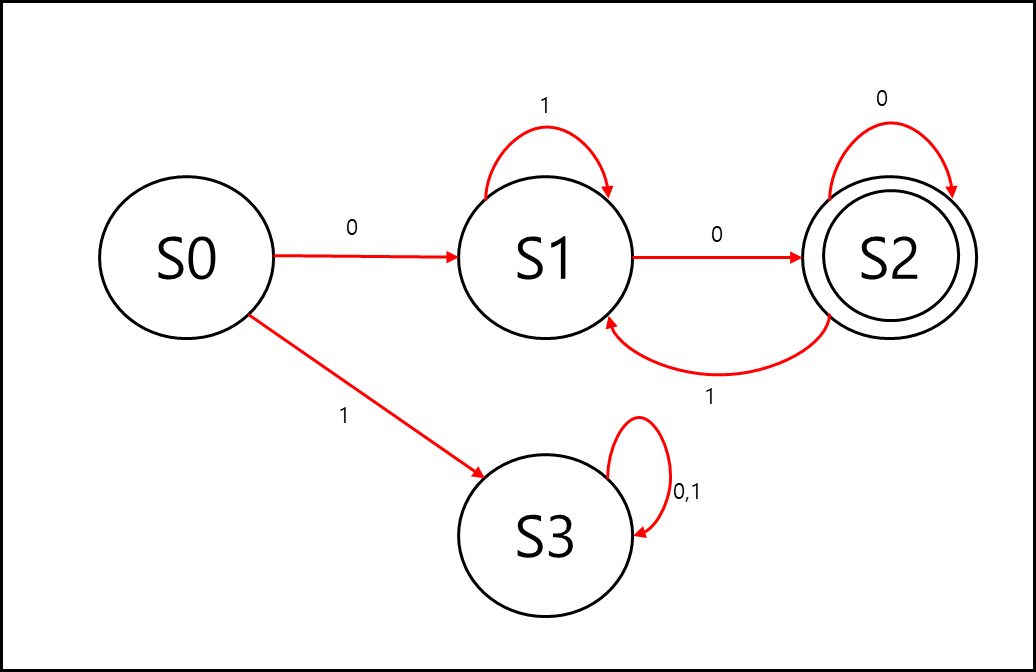
전이가 발생하지 않을 수 있다. 이를 그림으로 나타내면 아래와 같이 나타낼 수 있다.
뭔가 많이 빠져있는데, S0에서 1은 상태 전이가 없기 때문에 무시하고, S2에서 0과 1은 상태 전이가 없기 때문에 무시한다.
또한 S1에서 같은 0이라도 다수의 경로가 있는것을 확인 할 수 있다.
위와 같은 형태를 비결정 유한 상태 오토마타라고 한다.
기본적으로 NFA는 DFA로 변환 가능하기 때문에 사실상 둘은 같다고 볼 수 있다.
3. 유한 상태 오토마타를 이용한 스트링 매치 알고리즘
입력된 스트링에서 정해진 패턴을 찾는 문제에 유한상태 오토마타를 이용할 수 있으며
이 방식은 검색 또는 파싱에 응용 가능하다. 그렇다고 가장 효율적인 알고리즘은 아니지만 오토마타를 논할때 빠질수 없으며
어휘분석기에서 식별자와 토큰을 분할할때 사용하는 방식이다.
아래와 같은 문자열 패턴을 인식하는 유한 상태 오토마타가 있다고 해보자.
대상 문자열 : “abc”
빈 문자열인 처음 상태를 λ, 입력 문자의 집합은 {‘a’,’b’,’c’}이고 최종 상태가 S2라고 할때
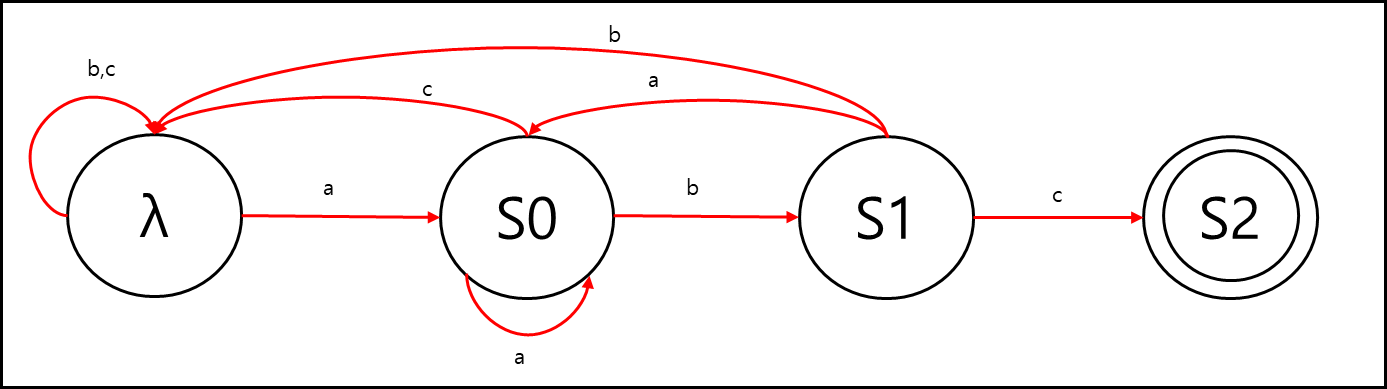
위 문자열을 인식하는 유한 상태 오토마타를 DFA로 나타내면 아래와 같다.
입력 문자열이 “abbabcb” 일 때 위 오토마타는 abc라는 패턴을 인식 할 수 있다.
문자열 “abbabcb” 중간에 abc가 있는 것을 찾아낼 수 있기 때문이다.
입력 문자열에 문자를 하나씩 입력해가면 state를 변경하다가 최종 상태에 도달할 수 있다면 해당 패턴이 있는 것이고
위와 같은 방법으로 토큰을 분할 할 수 있다.
단, 코딩을 해보면 알겠지만 토큰으로 인식해야할 것들이 매우 많고, 한 개의 문자에서 그 다음 입력에 따라 다수의 상태로 전이가 가능하므로
다수에 패턴에 대해 한 개의 문자를 확인한 뒤 처리해서 성능을 올리며(flex 계통), 가장 긴 매치와 우선 순위 규칙에 따라서 어떤 토큰인지 결정한다.
왜 가장 긴 매치와 우선 순위 규칙이 필요한지 알기 위한 간단한 예를 들자면 특정 식별자가 있다고 했을 때 사용자가 정의한 토큰이 해당 식별자를
substring으로 갖고 있다면 어느쪽으로 처리해야할지 결정하기 어려워지는 문제가 생기는데, 이럴때 가장 긴 매치를 먼저, 동일 길이에 대해서 우선 순위 규칙을
적용한다면 위와 같은 상황에서 결정할 수 없는 문제가 발생하지는 않는다.
4. Thompson’s construction(McNaughton-Yamada-Thompson algorithm)
사실 정규표현식은 NFA(비결정 유한 상태 오토마타)로 전환이 가능하다.
이를 가능케하는 것이 바로 톰슨의 구성(제목 보면 알겠지만 줄임말이다)이라는 알고리즘이다.
이렇게 전환한 NFA는 이후 DFA로 전환하거나 NFA를 직접 시뮬레이션 할 수 있다.
기본적으로 톰슨의 구성을 사용하면 단일 시작 상태와 단일 최종 상태를 갖는 NFA를 만들수 있기 때문에 구조적으로 매우 편리하다.
이 톰슨의 구성의 요지는 이거다.
모든 정규표현식을 구성하는 부분 요소를 NFA로 만들 방법이 있으며 이를 잘 조합하면 모두 표현 가능하다
사실 아닐 수도 있지만 일단 내가 이해하기로는 이랬다.
일단 정규식은 크게 나누면 or(+ 혹은 |로 표기), and(ab와 같은 꼴), 그리고 Kleene star라고 불리는 *가 있다.
위 표현에 대해서만 각기 표현할 수 있다면 조합해서 NFA를 만들수 있다.
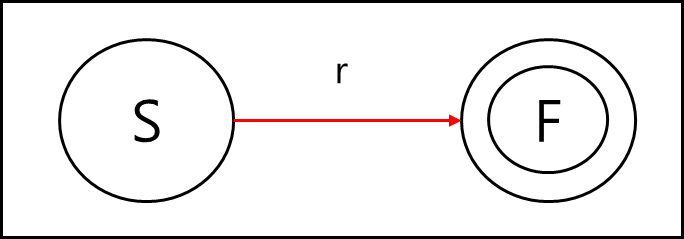
알파벳의 집합을 구성된 정규식의 r이 있다고 해보자.
시작상태가 S고 최종 상태가 F라고 할때 정규식 r의 내부가 어떻든 아래와 같이 표현 가능하다.
정규식 r이 $\alpha$ 라는 임의의 문자열로 이루어져있다고 해도 r을 $\alpha$ 로 그대로 치환하면 성립하는 형태이다.
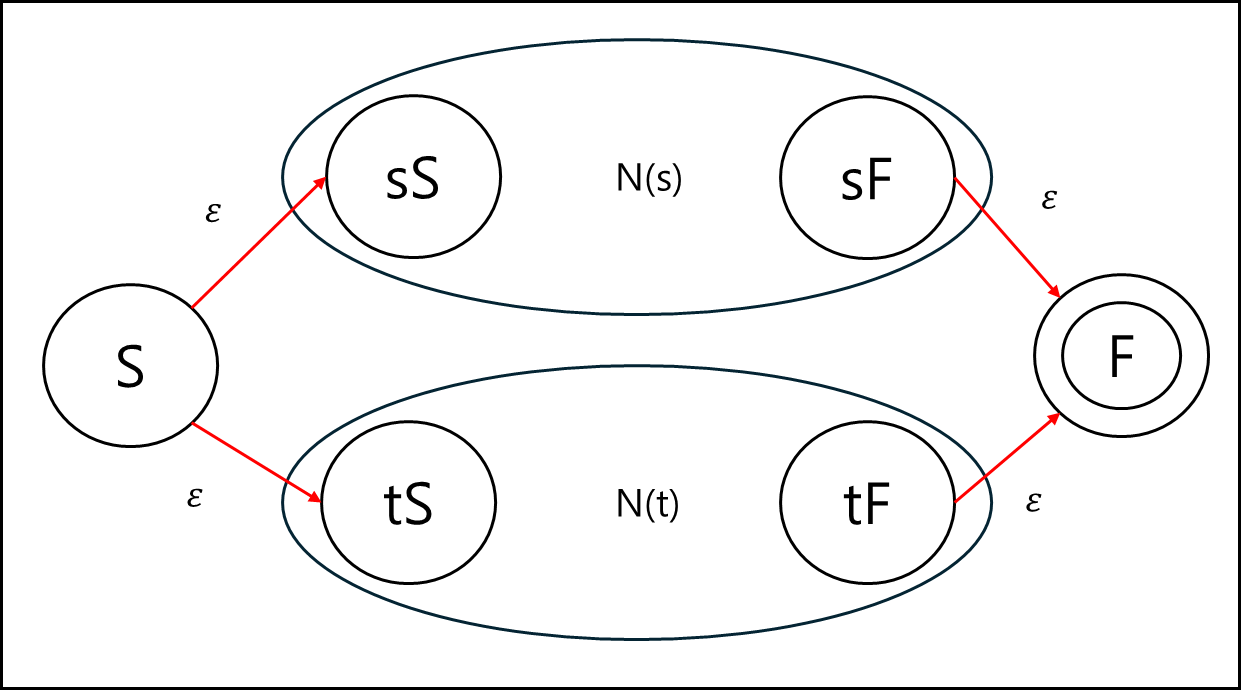
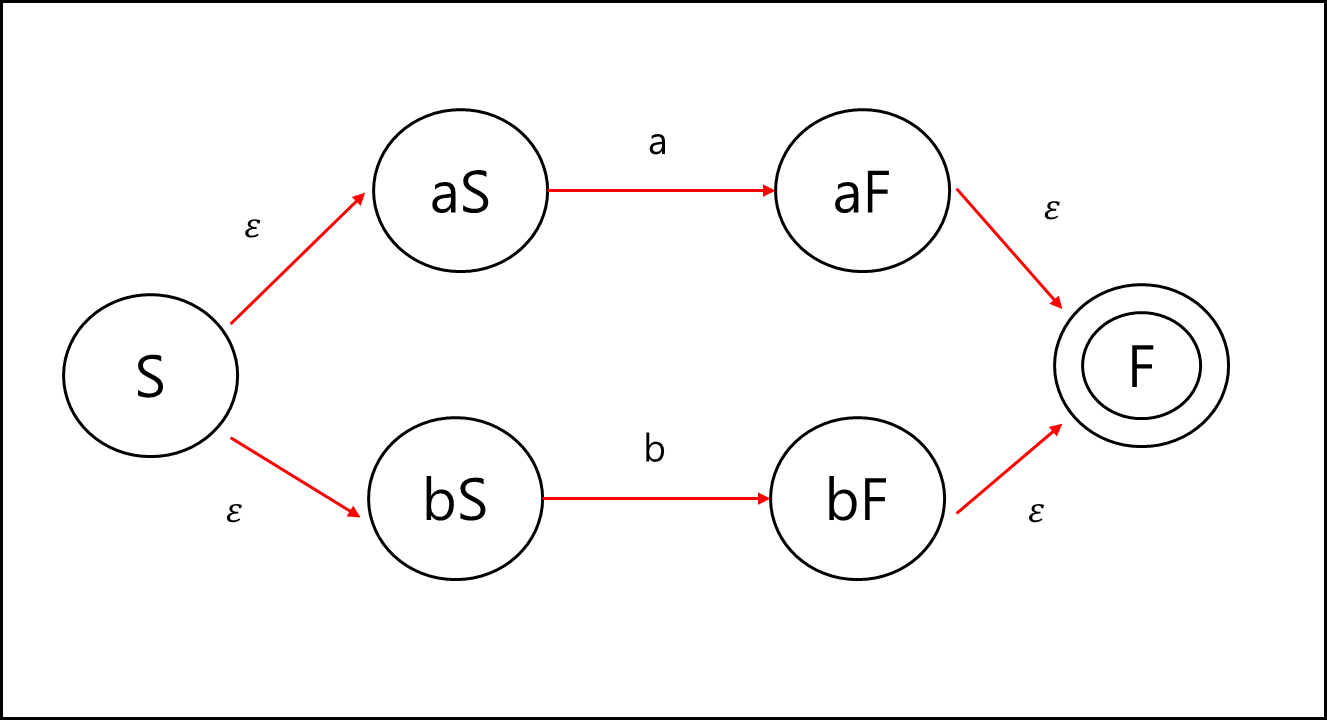
만약 a|b와 같은 형태의 서로 베타적 형태이지만 둘이 합쳐서 정규식 r을 이루는 형태의 정규식이라고 해보자.
이 베타 부분집합을 각각 N(s)와 N(t)라고 할때 표현은 아래와 같이 나타낼 수 있다.
여기서 입실론은 입력 없는 전이이다. 어느쪽이든 이동 가능하다는 것을 표현하기 위한 공입력이라고 생각하면 편하다.
시작 상태에서 N(s)의 시작상태이든 N(t)의 시작상태로든 한 군데로 전이해야 최종 상태로 전이가 가능하며
어느 한쪽이든 전이된다면 해당 부분 정규식의 최종상태에 도달해야 최종 상태로 전이할 수 있다.
단, a|b의 정규 표현식에서 알 수 있 듯이 둘이 같이 나오면 안된다. 때문에 상태 전이도에서도
N(s)와 N(t)는 서로의 최종 상태에 영향을 미치지 않지만 둘 중 하나여야 최종상태에 도달할 수 있는 형태임을 알수 있 다.
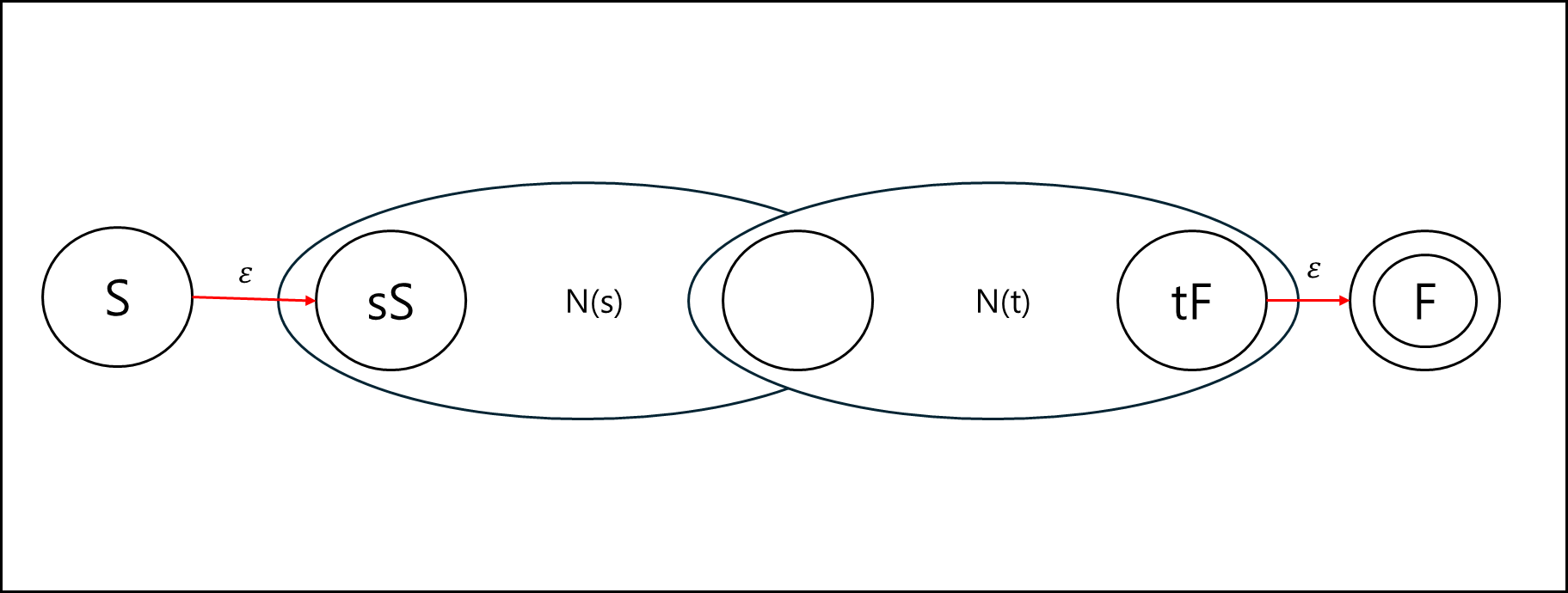
ab와 같이 and 형태라면 전이도는 아래와 같이 표현할 수 있다.
N(s)의 시작 상태로 전이 후 N(s)의 최종 상태로 전이시 N(t)의 시작상태로 전이하게 되고
이후 N(t)의 최종 상태로 전이하면 전체 최종 상태로 전이하는 형태이다.
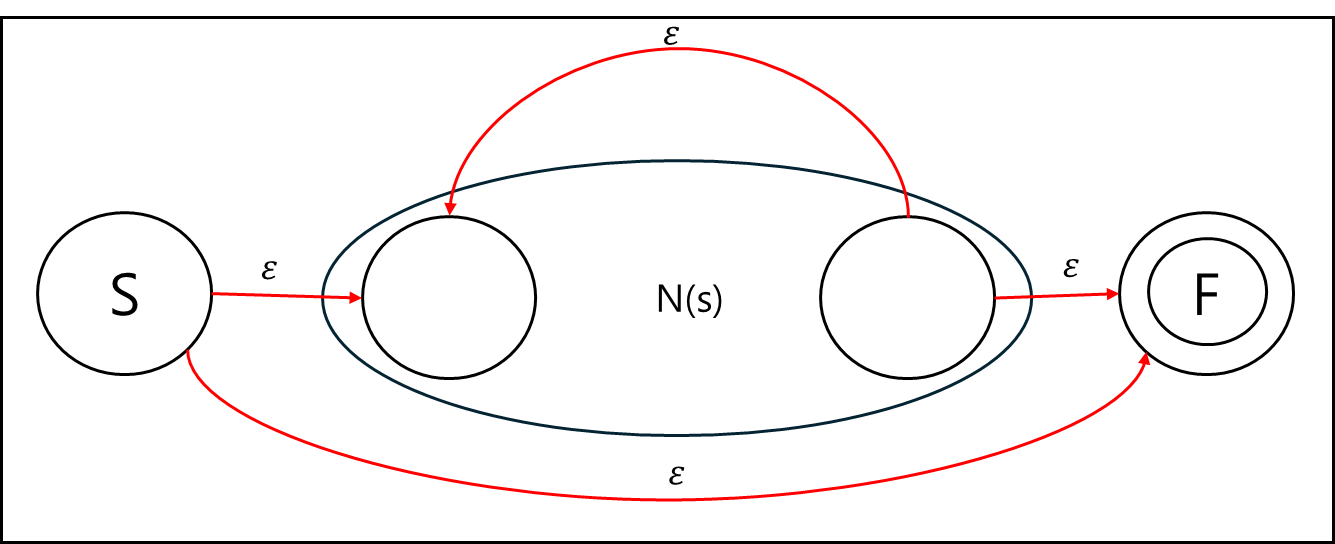
a*와 같이 kleene star는 아래와 같이 표현 가능하다.
정규표현식으로 생각해보자면 a가 없어도 되고, 1개여도 되고 n개여도 되는 형태이기 때문에
시작 상태에서 바로 최종 상태로 전이하는 경우가 있고, a에 대해서 표현하는 N(s)에서 재귀적으로 전이 가능한 것을 알 수 있다.
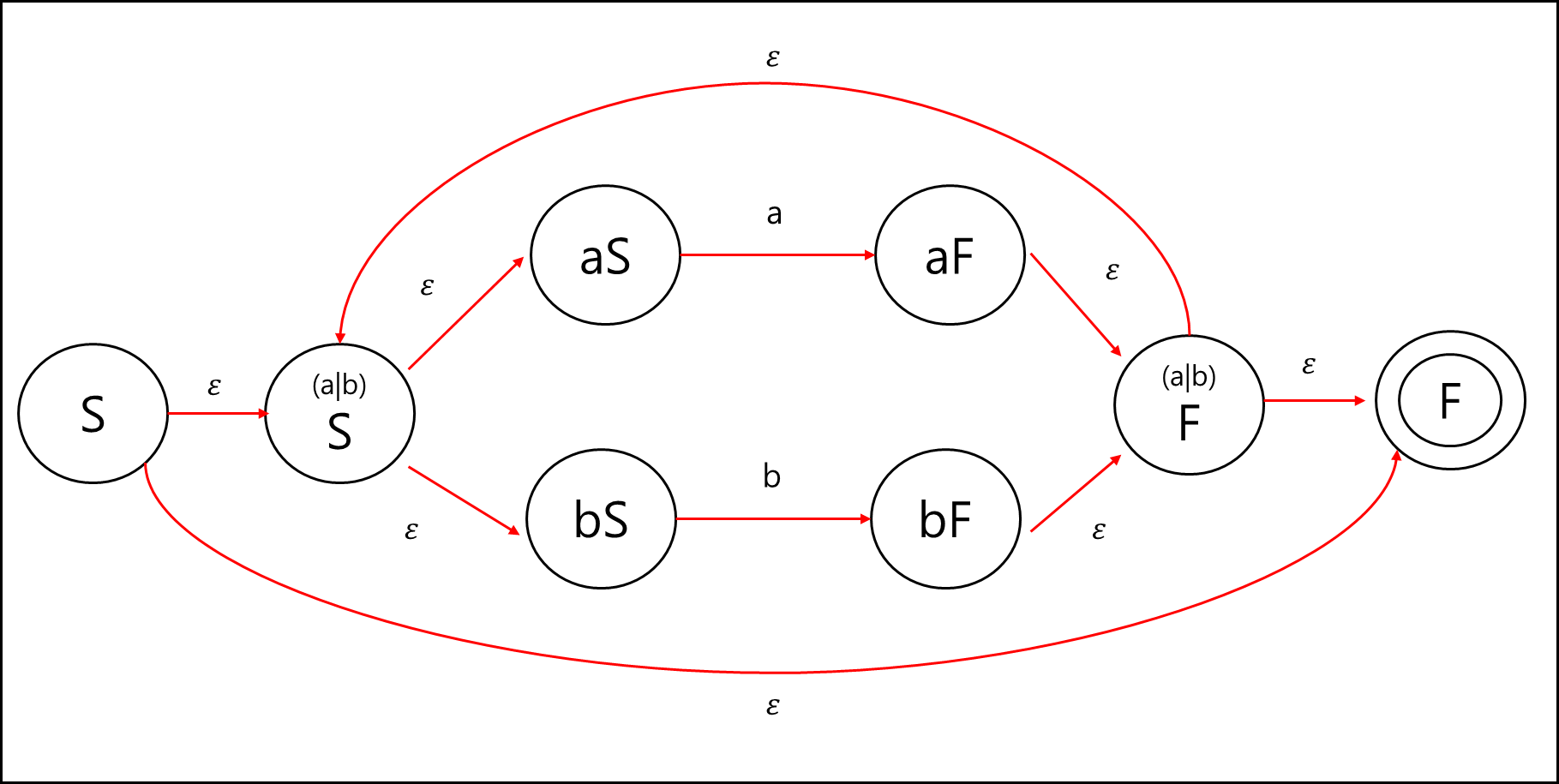
간단히 예시를 들어보겠다. 정규 표현식 $(a|b)^{*}ab$ 를 NFA로 만들어 상태 전이도로 표현해보겠다. 먼저 각 식을 부분 정규식으로 나눌 수 있다.
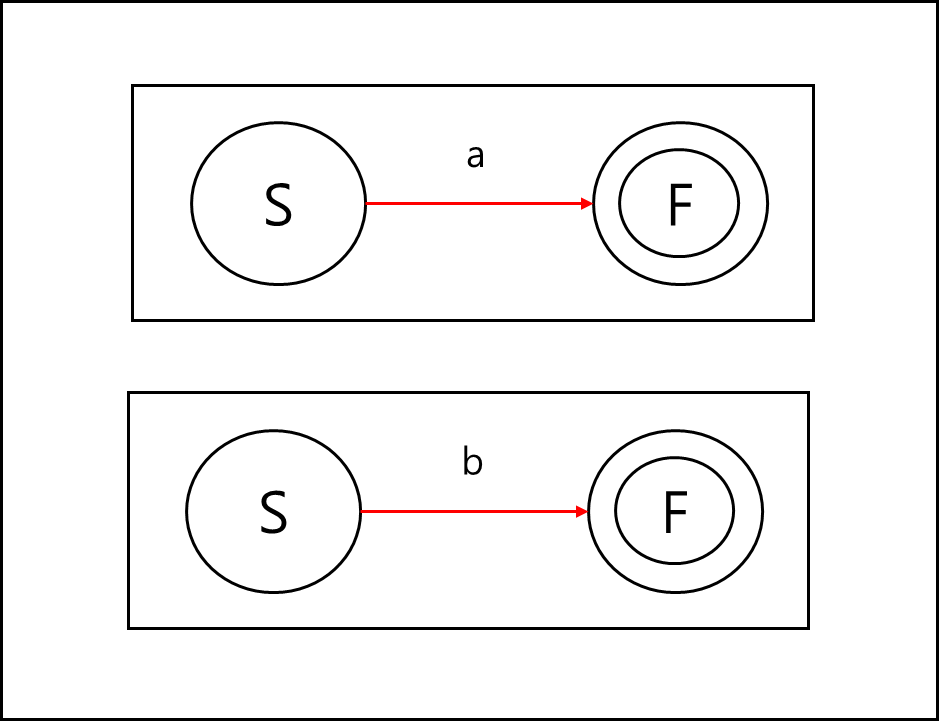
각각 정규표현식의 | 로 나뉘어있는 a와 b는 아래와 같이 나타낼 수 있다.
이렇게 표현 가능한 식을 위에서 설명한대로 |로 엮는다.
a|b까지는 표기되었고, 이후 이 a|b에 대해서 kleene star를 적용하면 아래와 같이 표현 가능하다.
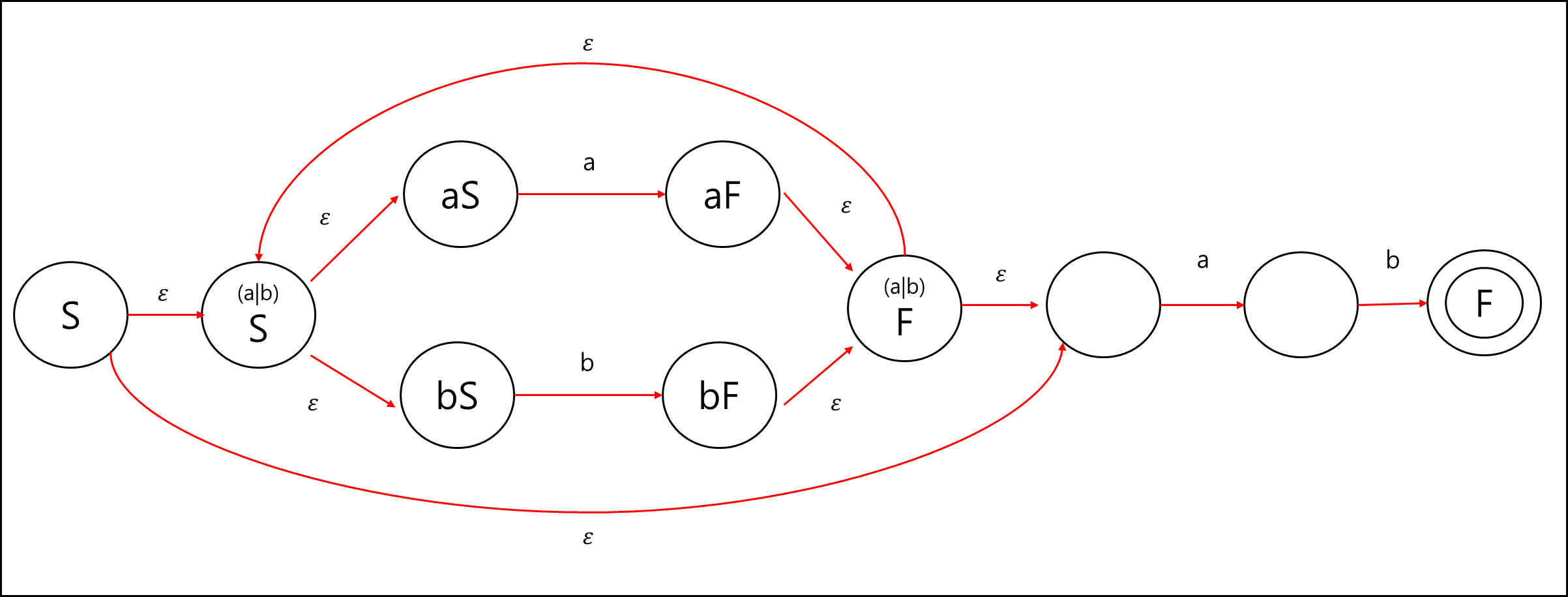
이후 ab를 붙이면 정규 표현식 에 대한 NFA 상태 전이도가 완성된다.
추가 업데이트 및 검증 예정
참고자료
- 유튜브 이산수학 - 이산수학: 형식언어와 오토마타3 - 유한상태기계(finite state machine)
- 유튜브 이산수학 - 이산수학: 형식언어와 오토마타4 - 오토마타와 언어
- widipedia - Thompson’s construction
- 컴파일러 : 원리, 기법, 도구 제 2판. ALFRED V. AHO, MONICA S. LAM, RAVI SETHI, JEFFREY D. ULLMAN. 우원희, 신승철, 우균, 하상호 옮김