컴파일러 - 어휘분석기 - 형식언어

Posted Aug 12, 2025 Updated Aug 15, 2025

By Blake Woo 9 min read

형식언어

1. 형식언어

구조, 범위 등이 명확히 규정되어 있는 언어. 자연 언어의 문법 구조를 수학적 측면에서 형식화한 것으로서 자연 언어보다 훨씬 간단한 구조의 인공 언어로 볼 수 있다. 형식 언어의 이론은 알골 등의 프로그램 작성 언어에서 제반 문제로 응용되고 있다.

형식 언어는 알파벳으로부터 생성되는 모든 문자열의 부분집합을 말하는데 이러한 언어는 문법에 의해서 생성되고 정의된다. 언어가 인식이 되려면 인식기가 필요하고 이 인식기는 문법에 따라 종류가 나뉜다.

노엄 촘스키가 만든 촘스키 위계에서는 아래와 같이 문법, 언어, 인식기를 정의한다.

문법	언어	인식기
type 0(무제약 문법)	재귀 열거 언어	튜링 기계(turing machine)
type 1(문맥인식 문법)	문맥인식 언어	선형한계 오토마타(linear-bounded automata)
type 2(문맥자유 문법)	문맥자유 언어	푸시다운 오토마타(push-down automata)
type 3(정규 문법)	정규 언어	유한 오토마타(finite automata)

TYPE 3 정규 문법

정규 표현식이 이 위계에 속하며 어휘 분석기에 사용된다.

TYPE 2 문맥 자유 문법

프로그래밍 언어의 구문 파서가 이 위계에 속한다.

TYPE 1 문맥 인식 문법

자연어의 일부 복잡한 구조를 이론적으로 모델링할 때 사용되지만 컴파일러에서는 잘 쓰이지 않는다.

TYPE 0 무제약 문법

가장 표현력은 크지만 현재 사용하는 곳은 없다.

2. 형식 문법

1) 정의

a 형식 문법 G=($V_{N}$,V_{T},P,S) 정의

$V_{N}$ : non-terminal 기호들의 유한 집합(직접 사용되지 않는 표현 - ex: “수식”, “질의”)
$V_{T}$ : terminal 기호들의 유한 집합(직접 사용되는 표현- ex: “if”, “else”)
$V_{N} \cap V_{T} = \varnothing, V_{N} \cup V_{T} = V$
P : 생성 규칙(production rule)의 집합으로 다음과 같다.
$ \alpha \to \beta, \alpha \in V^{+} , \beta \in V^{*} $
$\alpha$를 왼쪽 부분, $\beta$를 오른쪽 부분, $\to$는 왼쪽부분에 있는기호가 오른쪽 부분에 있는 기호로 단순히 대체
S : $V_{N}$에 속하는 기호로서 다른 non-terminal 기호들과 구별하는 start symbol

b. 유도(Derivation)

$\Rightarrow$는 유도한다는 뜻으로 만약 $\alpha \to \beta $가 존재하고, $\gamma$, $\gamma , \delta \in V^{*}$이면 $\gamma \alpha \delta \Rightarrow \gamma \beta \delta$로 표시
즉, 한 문자열에서 생성규칙을 한번 적용해서 다른 문자열로 바꾸는 것을 나타낸다.
$\overset{*}{\Rightarrow }$ : 영 번 이상의 유도(zero or more derivation)
$\overset{+}{\Rightarrow }$ : 한 번 이상의 유도(one or more derivation)

c. 문장 형태(sentential form)

$S \overset{*}{\Rightarrow} w$이고 $w$가 $V^{*}$에 속하면 $w$를 문장 형태(sentential form)라고 한다. $w$가 $V_{T}^{*} $에 속할 경우, $w$를 문장(sentence)이라 한다.

2) 표기법

a. 정규표현(Regular Expression)

이전 포스팅 참고

b. BNF(Backus - Naur Form) 표기법

프로그래밍 언어의 formal definition을 위해 가장 널리 사용되는 방법
이 표기법은 메타 기호(meta-symbol : 표현하려는 언어의 일부분이 아니라, 그 언어를 표현하려고 사용된 특수기호)로서 세가지 기호를 사용
- 논터미널 기호는 <와>로 묶어서 사용
- 대체(relplacement)를 나타내기 위해 ::=를 사용
- 양자 택일을 나타내기 위해 |를 사용

가령 식별자는 아래와 같이 나타낼 수 있다.

<식별자>::= <영문자>|<식별자><영문자>|<식별자><숫자>   
<영문자>::=a|b|c|...|z   
<숫자>::=0|1|2|...|9   

만약 식별자의 길이가 길어야 5라고 하면 BNF 표기법으로 아래와 같이 표현 가능하다.

<식별자>::= <영문자>|<영문자><영문자>|<영문자><숫자>|<영문자><영문자><영문자>|     
           |<영문자><영문자><숫자>|<영문자><숫자><영문자>|<영문자><숫자><숫자>|     
           ....    
           |<영문자><숫자><숫자><숫자><숫자>     
<영문자>::=a|b|c|...|z   
<숫자>::=0|1|2|...|

위와 같이 반복될 경우 표기가 매우 어려워진다. 이러한 반복표시를 쉽게 해결하는 법이 EBNF이다.

c. EBNF(Extended BNF)

BNF 표기법은 반복되는 부분을 표시하는데 어려움이 있다.
반복되는 부분을 나타내기 위해 메타 기호로 {}와 <와>를 사용
- {a}는 a가 0번 이상 반복될 수 있음을 의미
선택적인 부분을 표시할시에 []로 표현
메타기호를 terminal 기호로 사용하는 경우에는 기 기호를 ‘와 ‘로 묶어서 표현

이전에 식별자 길이가 최대 5자라고 할때 이를 EBNF로 표현하면 아래와 같다.

<식별자> ::= <영문자>{< 영숫자 >}^7_0   
<영숫자> ::= <영문자> | <숫자>   
<영문자> ::= a | b | c | ··· | z   
<숫자> ::= 0 | 1 | 2 | ··· | 9   

식별자의 ^7은 윗 첨자로 7, _0은 아래첨자로 0이 들어가있다는 뜻이다.

d. 구문도표(Syntax Chart)

구문 도표는 순서도와 유사하게 그림(도표)으로 구문을 표현하는 것이다.
EBNF와 일대일 대응이 된다.
초기 Pascal의 사용자 설명서에 사용되었다.

도형	의미
□(사각형)	비단말 기호
○(원)	단말 기호
→(화살표)	기호 연결

가령 EBNF로 아래와 같은 수식이 있다고 해보자.

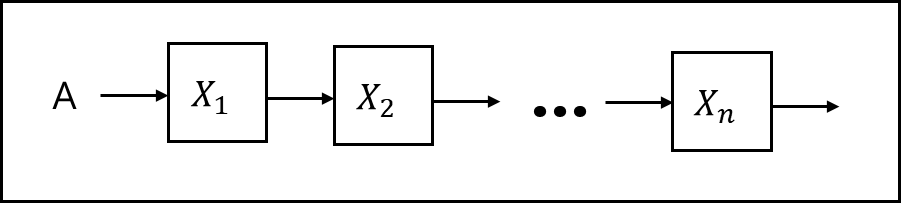
A :: = $X_{1}X_{2}…X_{n}$ (단, $X,X_{1}…,X_{n}$은 비단말 기호이다.)

위의 수식은 아래의 구문도표로 표현이 가능하다.

참고자료

순천향대학교 KOCW - 컴파일러
위키백과 - 형식언어
정보통신용어사전 - 형식언어
Knowledge Repository - 프로그래밍 언어의 구문의 표현 - BNF, EBNF, 구분 도표 표현법
컴파일러 : 원리, 기법, 도구 제 2판. ALFRED V. AHO, MONICA S. LAM, RAVI SETHI, JEFFREY D. ULLMAN. 우원희, 신승철, 우균, 하상호 옮김
위키백과 - 촘스키 위계

Compiler

Compiler Language

This post is licensed under CC BY 4.0 by the author.