컴퓨터 구조 - CPU 구조 - 분기 예측(Branch Prediction)
Branch prediction
1. 개요
분기문은 비용이 큰 명령중 하나다. 5-stage pipeline에서 분기문이 발생하면 다음 명령어를 어떤 것을 실행해야할지 알수가 없고, 예측해서 명령어를 갖고 온다고 한들 해당 예측이 틀려버리면 파이프라인 전체를 비워버려야하기 때문에 다수의 사이클을 허비하게 된다.
때문에 현대의 CPU는 분기 예측을 좀 더 잘 할 수 있게 회로 구성이 되어있다.
2. 분기 종류에 따른 예측의 어려움
1) 분기문
IF 문과 같은 경우 혹은 while과 같은 loop를 도는 경우를 말한다.
- 실제로 이 if가 true(이하 taken)일지 false(이하 not taken) 일지 예측하기 어렵다
- 분기문이 어디를 Target으로 하는지 예측하기는 상대적으로 쉽다 PC + offset으로 Target을 설명할 수 있는데 이 offset은 링킹과정에서 다 정립되기 때문이다.
2) 무조건 Jump
무작정 JUMP 하는 경우를 말한다. 무한 Loop의 경우라던지 (중간에 break 문이 있다면 이는 분기문에 해당한다)
X86 어셈블리어로 JMP 같은 명령어를 말한다.
- 항상 jump 하므로 condition에 대한 예측은 필요없다.
- 어디로 jump 할지 명확하다. 분기문과 동일하게 PC + offset으로 나타낼 수 있다.
3) 레지스터에 담긴 주소로 이동하는 경우(Function call, function return)
함수 호출이나 함수를 마친뒤 리턴 할 때 같은 경우를 말한다.
- 항상 jump 하므로 condition에 대한 예측은 필요없다.
- 어디로 jump할지 예측은 어렵다 (레지스터에 담겨있으므로 동적이다)
3. 분기문 종류에 따른 예측
무작정 예측을 하는 Static한 예측법도 있지만 여기서는 경우에 따라서 Dynamic 하게 예측하는 예측법에 대해서 말한다.
1) 분기문 Condition 예측
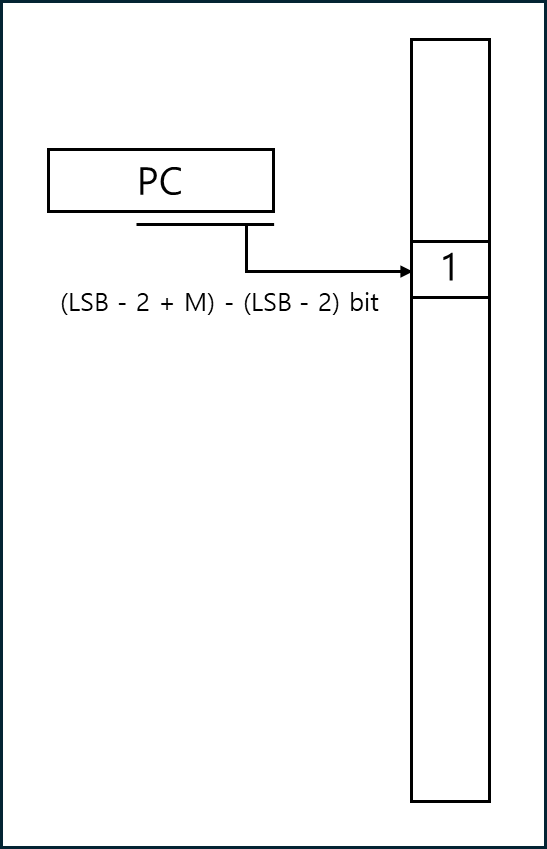
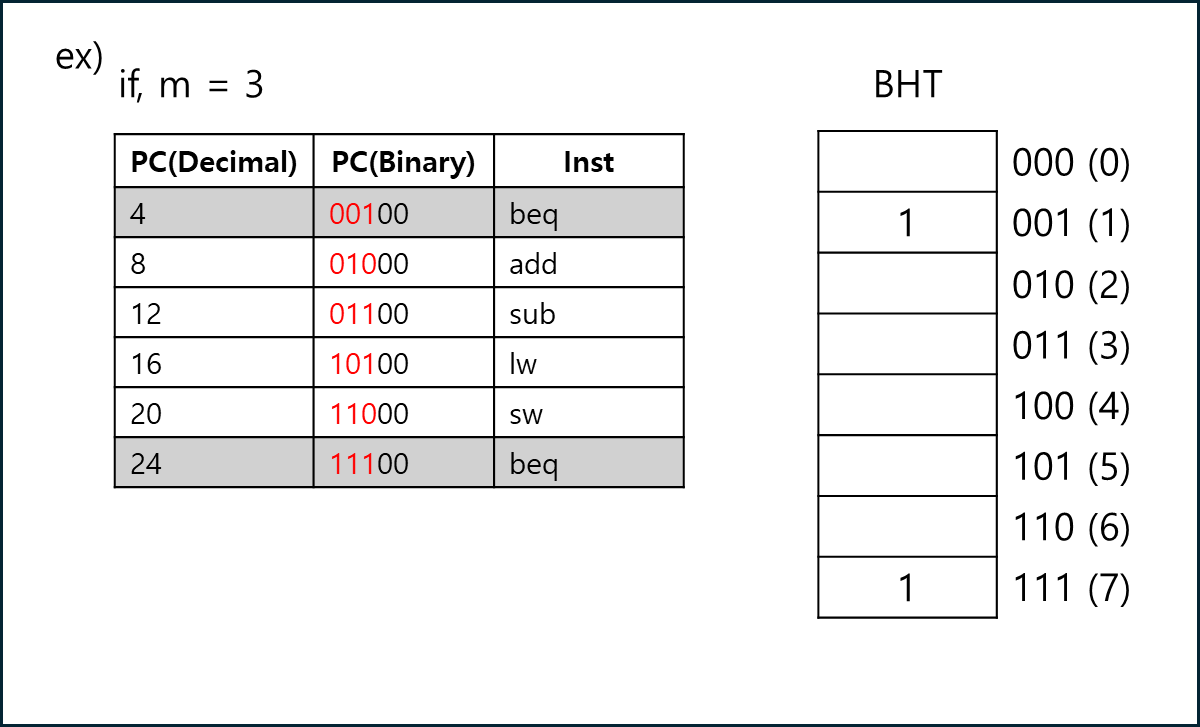
BHT(Simple Branch History Table)이라는 방법이 있다. 다음 분기는 이전 직전것과 같을 것이다라는 생각에서 시작된 예측법이다.
기본적으로 $2^{M} \times 1$ bit 만큼의 테이블을 유지하며, PC 값의 LSB - 2bit에서(주소 체계에서 뒤에 2비트는 의미가 없다) M개만큼을 INDEX로 사용해서 이전에 분기 했다면 1 아니라면 0으로 기재해두는 것이다. 만약 예측이 성공했다면 그대로 두고, 예측이 실패했다면 해당 TABLE을 고친다.
아래는 예시이다.
2) 분기문의 Target 예측
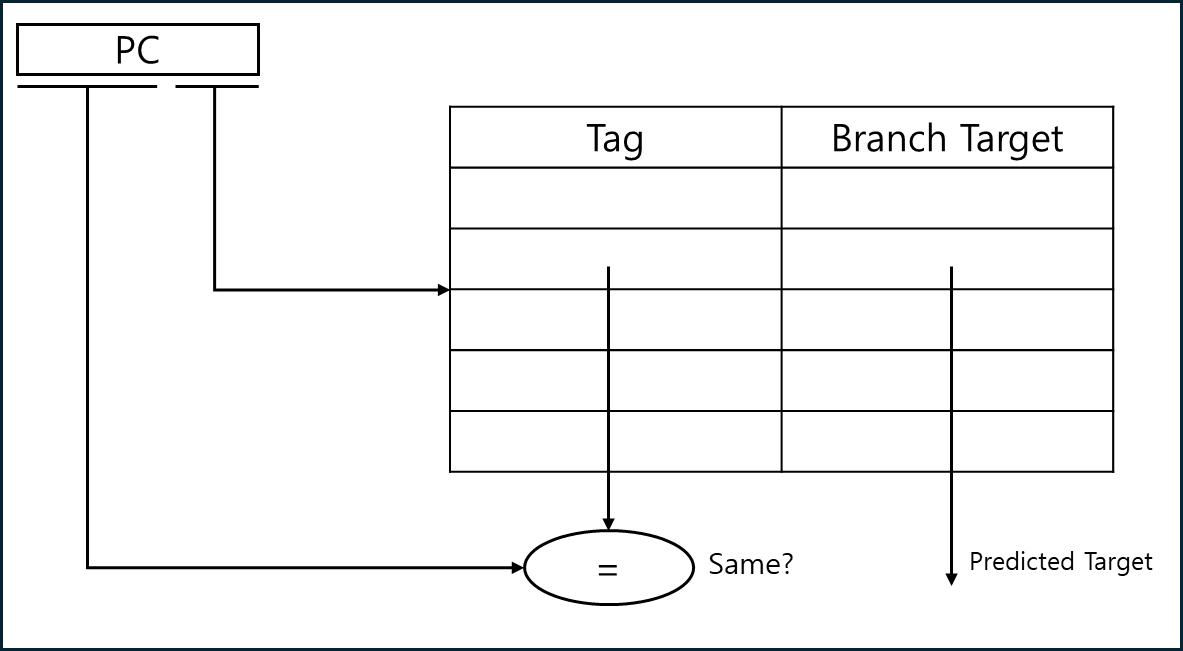
BTB(Branch Target Buffer)라는 방법이 있다.
말 그대로 이전 Branch에 대한 기록을 캐싱해둔 테이블이라고 생각하면 된다. taken이 된 분기문에 대해서 테이블을 유지하며 Tag와 Branch Target을 기재해둔다. 여기서 Tag 값은 LSB를 뺀 BIT를 tag로 사용하는데 이는 다른 Task가 해당 값을 함부로 갖다 쓰지 못하게 하기 위해서이다.
3) RAS(Return Address Stack)
Function call의 경우 주소가 변동되기 때문에 별도의 Stack을 둔다.
CPU에 하드웨어적으로 구현된 Stack(Last In First Out)인데, 함수를 Call 할때마다 Call된 주소를 해당 Stack에 집어넣는다. 일반적으로 RAS의 크기는 8 ~ 16 정도이며 해당 함수에서 return을 반환할 경우 RAS에서 주소를 Pop하여 PC에게 반환한다.
만약에 RAS 크기보다 더 큰 개수의 주소가 들어온다면 어떨까? 그러면 가장 오래전에 넣은 주소부터 사라지기 시작하며
이 주소의 경우 Main Momory Stack에서 갖고오던가 해야할 것이다.
참고자료
- Computer Organization and Design-The hardware/software interface, 5th edition, Patterson, Hennessy, Elsevier
- Quora - How are CPU return address stack branch predictors designed? by John Redford
- 서강대학교 이혁준 교수님 강의자료 - 고급 컴퓨터 구조