통계학 - 자료의 정리2
이변량 자료와 상관계수
1. 변수 개수에 따른 분류
1) 일변량 자료(univariate data)
하나의 변수에 대한 자료
2) 이변량 자료(bivariate data)
두개의 변수에 대한 자료
3) 다변량 자료(multivariate data)
여러 개의 변수에 대한 자료
2. 자료 분석
1) 두 변수가 모두 질적 자료인 경우
첫번째 자료는 r개의 범주, 두번째 자료는 c개의 범주.
이러한 자료를 행렬의 형태로 요약한 표를
r x c 분할표(rxc contingency table) 이라고 한다.
ex)
성별에 따른 문제 난이도 표를 2 x 3 분할표로 표기
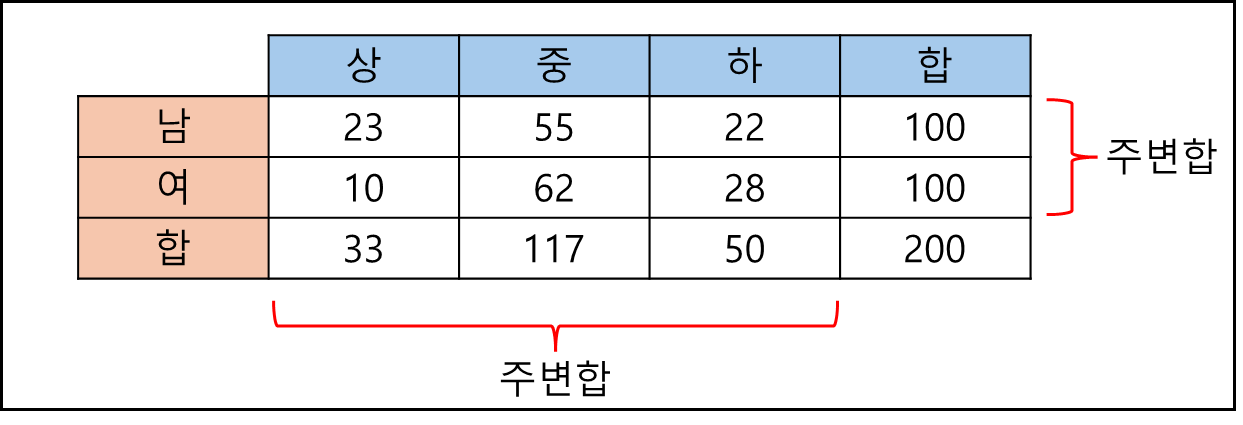
2) 두 변수가 모두 양적 자료인 경우
$x_{i}$는 i번째 자료의 첫번째 변수, y_{i}는 i번째 자료의 두번째 변수일때 n개의 이변량 자료는 아래와 같이 표현한다.
\[(x_{1},y_{1}),...,(x_{n},y_{n})\]위와 같은 자료의 경우 아래와 같은 형태로 표현할수 있다.
a. 산점도
이차원 평면에 각 변수의 값에 해당되는 점을 찍은 그림
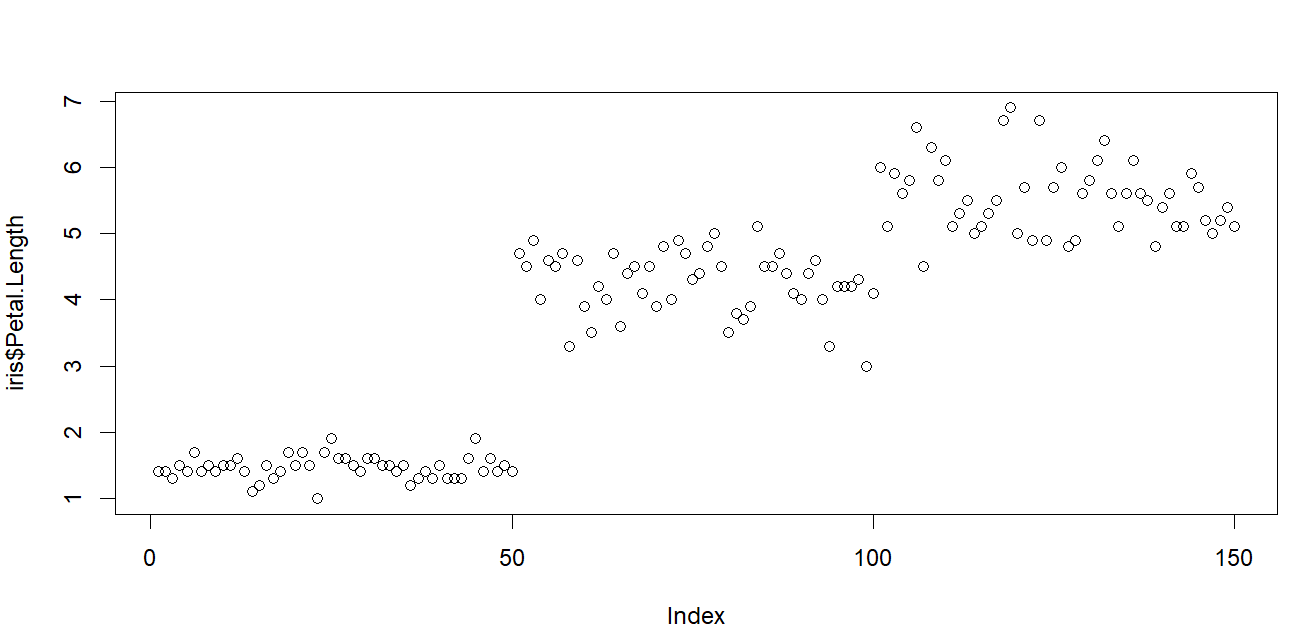
산점도를 그렸을때 전체적으로 우상향을 그린다면 양의 상관관계(Positive Correlation) 우하향을 그린다면 음의 상관관계(Negative Correlation), 무작위라면 직선적 상관관계 없음(No Correlation)이라 부른다.
3. 허위상관과 잠복변수
두 개의 변수가 높은 상관관계를 보이는 것처럼 보이나 사실은 숨어있는 어떠한 요인(잠복변수)때문에 높은 상관관계가 있는 것처럼 보이는 것을 허위 상관이라고 한다.
ex) 첫번째 변수 : i번째 도시의 범죄 건수 두번째 변수 : i번째 도시의 학교 수
매우 높은 상관관계를 보이나 사실은 인구라는 잠복 변수로 인해 높은 상관관계를 보이게 됨.
이런 경우 허위 상관
4. 표본 상관계수
두 변수의 선형적 함수 관계를 나타내는 측도 (비 선형적인 것은 알 수 없음)
표본 상관계수 r은 아래와 같이 구한다.
※ 참고
$S_{xx} = \frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}$ : X의 분산
$S_{yy} = \frac{1}{n-1}\sum_{i=1}^{n}(y_{i}-\overline{y})^{2}$ : Y의 분산
$S_{xy} = \frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})$ : X,Y의 표본 공분산
분산에 대한 설명은 이곳 을 참고하라.