통계학 - 통계적 추론 - 점추정, 구간 추정
통계적 추론
모집단에서부터 표본을 추출하여 모집단의 특성을 나타내는 모수(알려져 있지 않은 상수)에 대한 여러가지 정보를 얻기 위한 일련의 과정
통계적 추론 = 추정(estimation)[점 추정(point estimation) + 구간 추정 (interval estimation)] + 가설검정(test of hypotheses)
1. 점 추정
추정하고자 하는 하나의 모수에 대하여 모집단에서 임의로 추출된 표본 n개의 표본의 확률 변수로 하나의 통계량을 만들고 주어진 표본으로부터 그 값을 계산하여 하나의 값을 제시하는것이다.
모수를 추정하기 위해 만들어진 통계량을 추정량(estimator)라고 하고, 주어진 관측값으로부터 계산된 추정량의 값을 추정치(estimate)라고 한다.
어떤 모수 $\theta$에 대한 점 추정치 $\overline{\theta}=\overline{\theta}(X_{1},…,X_{n})$이 $E(\overline{\theta})=\theta$를 만족하면 $\overline{\theta}$은 $\theta$에 대한 불편 추정치(unbiased estimator)라고 부른다.
여기서 불편은 편향되지 않았다는 뜻이다.
아래는 흔히 쓰이는 점 추정치의 예시이다.
- $E(\overline{X}) = \mu$ : 표본 평균은 모평균에 대한 불편추정치
- $Var(\overline{X}) = \sigma ^{2} / n$ : 표본의 분산은 모분산에 대한 불편 추정치
- $s.d(\overline{X}) = \sigma / \sqrt{n}$ : 표준편차는 모표준편차에 대한 불편 추정치
- $s.d(\overline{X})$의 추정값 $s.e(\overline{X}) = s/ \sqrt{n}$(표준편차의 추정치) : 표준오차(standard error)
\(E(s^{2})=\sigma ^{2}\)
즉, $s^{2}$은 $\sigma ^{2}$에 대한 불편 추정치
임의 표본 $X_{1},…,X_{n}$이 성공 확률이 p인 베르누이 시행을 따를 경우
p에 대한 점 추정치 역시 표본평균을 사용하며
$X\equiv \sum_{i=1}^{n}X_{i}~B(n,p)$ 이므로 점 추정치는 $\hat{p} = X/n$
2. 구간 추정(Interval Estimation)
1) 대표본(Large Sample)
a. 신뢰구간
해당 구간에 모수가 포함될 확률을 말한다.
모수 $\theta$에 대한 $(1-\alpha)%$ (단, 0<$\alpha$<1) 신뢰구간:
\(P(L(\hat{\theta}))<\theta<U(\hat{\theta})) = 1 - \alpha\)
를 만족하는 구간
\((L(\hat{\theta}),U(\hat{\theta}))\)
※ 참고 : $\alpha$는 신뢰 수준(level of confidence)라고 하며, 흔히 아래와 같은 수를 가진다.
- $\alpha$ = 0.01 => 99% 신뢰구간
- $\alpha$ = 0.05 => 95% 신뢰구간
- $\alpha$ = 0.10 => 90% 신뢰구간
※ 참고2 : 여기서 L과 U는 각각 별도로 뽑아낸 표본이다. U는 구간의 상한값, L은 구간의 하한값을 뜻한다.
b. 모평균에 대한 근사적 신뢰구간
모평균 $\mu$에 대한 100(1-$\alpha$)% 근사적 신뢰구간은 아래와 같다.
가. 표준편차를 아는 경우
\(\overline{X} \pm Z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\)
나. 표준 편차를 모르는 경우
\(\overline{X} \pm Z_{\alpha/2}\frac{s}{\sqrt{n}}\)
일반적으로 모수 $\theta$에 대한 점 추정치를 $\hat{\theta}$라 하면,
모수 $\theta$에 대한 $100(1-\alpha)%$ 근사적 산뢰구간은
$\hat{\theta}\pm Z_{\alpha/2}s.e.(\overline{X})$으로 표현 가능하다.
c. 모비율에 대한 근사적 신뢰구간
표본에 대한 가정으로 $X_{1},…,X_{n}$인 성공의 확률이 p인 베르누이 시행이고,
np > 15, n(1-p) > 15를 만족한다면 아래와 같이 구할 수 있다.
가. 모비율 p에 대한 100(1-$\alpha$)% 근사적 신뢰구간
\(\hat{p} \pm Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)
2) 소표본
표본의 크기가 작을(25 이하)경우 구간 추정은 대표본일때와 조금 다르다.
소표본일 때는 임의 표본이 반드시 정규분포를 따른다는 가정이 필요하다.
이때는 Student t 분포를 사용한다.
a. Student’s t-분포
임의 표본 $X_{1},…,X_{n}$이 정규분포 $N(\mu,\sigma ^{2})$를 따를 경우
\(T = \frac{\overline{X}-\mu}{s/\sqrt{n}}\) \(= \frac{\overline{X}-E(X)}{s.e(\overline{X})}\)
는 자유도 (degree of freedom) n-1인 t-분포를 따르게 되며 T-t(n-1)으로 표현한다.
자유도 = 관측치 수 - 제약 조건의 개수
가. 분포의 형태
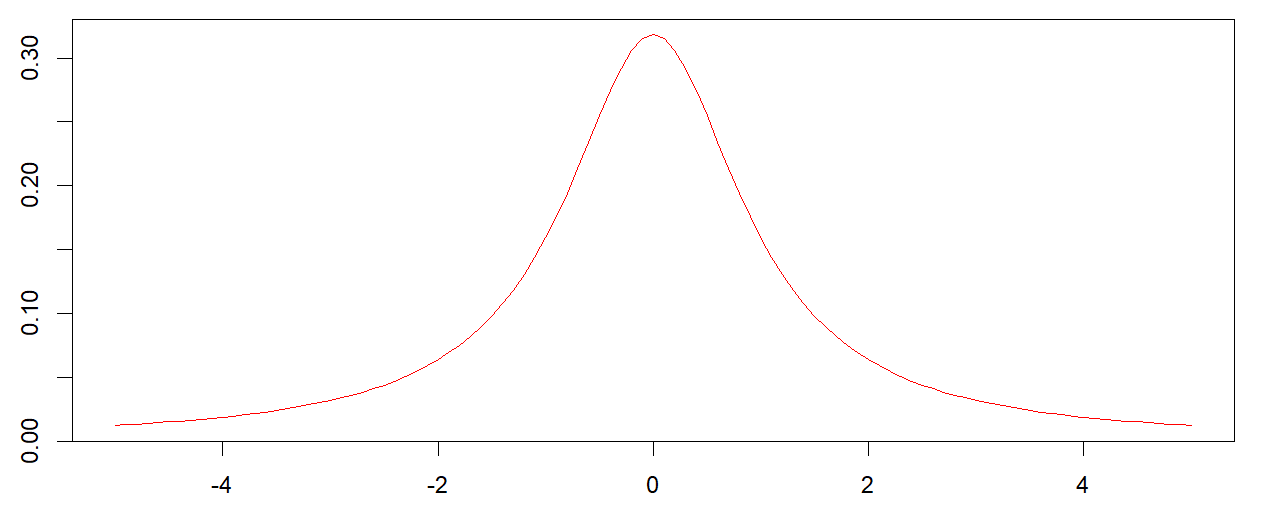
기본적으로 t분포는 정규분포에 비하면 양쪽 꼬리가 두껍다. 이 때문에 heavy-tailed distribution이라고도 불린다.
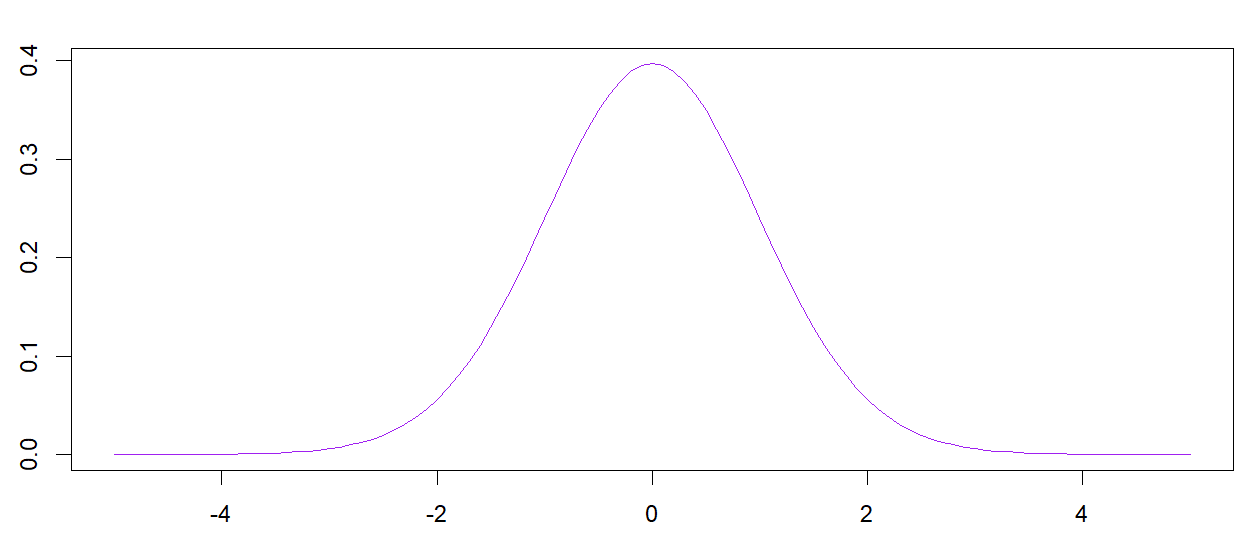
자유도가 높아질수록 꼬리가 얇아지며 자유도가 무한으로 발산할 경우 정규분포와 형태가 같아진다.
자유도가 1인 스튜던트 t 분포
자유도가 50인 스튜던트 t 분포
나. 신뢰구간
$X_{1},…,X_{n}$이 정규모집단 $N(\mu,\sigma ^{2})$로부터의 확률 표본이라 할때, 모평균 $\mu$에 대한 $100(1-\alpha$% 신뢰구간
\(\overline{X} \pm t_{\alpha/2}\frac{s}{\sqrt{n}}\)