트리
트리
점이 있고 이 점이 선으로 연결된 형태를 그래프라고 한다. 이러한 점은 각각 노드, 정점, vertex라고 불리며 연결한 선은 edge 혹은 간선이라고 부른다.
트리는 기본적으로 이러한 그래프에서 파생된 것이다. 순환이 없는 그래프라고 봐도 무방한데 순환이 없는 형태라면 필연적으로 한 개의 노드에서 모든 가지가 나오는 형태로 만들어진다. 이때 모든 가지가 파생된 한 개의 노드를 루트라고 부르며 루트에서 가장 말단이 몇 가지나 멀어져있느냐에 따라 깊이(depth)를 말한다. 또한 level이라고도 부른다. 기본적으로 루트의 level은 1이며 노드가 하나씩 멀어질때마다 1씩 증가한다 각 노드가 지닌 가지의 수를 차수라고 하며 각 가지에서 가장 말단에 있는 노드를 리프 노드라고 한다.
이러한 트리의 종류는 아래와 같다.
- Binary Tree
- Balanced Tree
- Full Binary Tree
- Perfect Binary Tree
- Complete Binary Tree
- M-way search tree(MST)
- B- Tree
- B+ Tree
- 2-3 Tree
- Red-Black Tree
- AVL Tree
차근 차근 하나씩 어떤 것인지 알아보겠다.
이진 트리 (Binary Tree)
한 개의 루트에서 여러 개의 간선이 뻗어서 노드에 연결된 형태라면 모두 트리이다. 이 중에 모든 노드가 2개 이하의 하위 노드를 가지는 트리를 이진 트리라고 부른다.
균형 이진트리(Balanced Tree)
말단 노드들의 깊이 차이가 1을 넘어가지 않는 형태를 말한다.
정 이진트리(Full Binary Tree)
모든 노드의 자식 노드가 0개 또는 2개인 트리를 말한다.
포화 이진트리(Perfect Binary Tree)
정 이진트리(Full Binary Tree)이되 모든 말단 노드의 자식 수와 깊이가 같은 트리를 말한다. 보기에 꽉 찬 이진 트리이다.
완전 이진트리(Complete Binary Tree)
제일 말단 노드의 깊이를 a라고 할때 a-1 깊이 까지는 포화 이진트리(perfect binary tree)이면서 a 깊이에서는 왼쪽 리프 노드부터 채워진 형태를 말한다.
다원 탐색 트리 (MST - Multiway search tree)
어떤 노드 A가 있을때 이 A는 최대 2개의 자식노드만 가지고 A의 왼쪽 자식 노드인 B는 A보다 무조건 작은 값을 가지고 A 노드의 오른쪽 자식 노드인 C는 A보다 무조건 큰 값을 가진 형태인 트리로 중복된 키를 허용하지 않으며 어떤 노드의 하위 노드를 트리로 구성해도 동일한 형태를 띄는 것을 이진 탐색 트리(BST - Binary Search Tree)라고 한다. 여기서 최대 자식이 2개가 아닌 여러개 일경우 다원 탐색 트리(MST - Multiway search tree)라고 부른다.
B- Tree
MST의 일종이며 M이 차수일 때 다음의 규칙을 갖는다.
- 루트를 제외한 노드는 M/2개 만큼의 자식을 가져야한다. 차수가 6개면 한 개의 노드는 최소 3개의 자식 노드를 가져야하는 것이다.
- 루트 노드는 아예 없거나 최소 2개의 자식 포인터를 가져야 한다.
- 모든 리프 노드는 똑같은 레벨이어야 한다.
- 노드의 생성은 아래에서 root로 향한다.
- 각 노드는 M-1개만큼의 키를 가질 수 있다.
키 삽입 절차
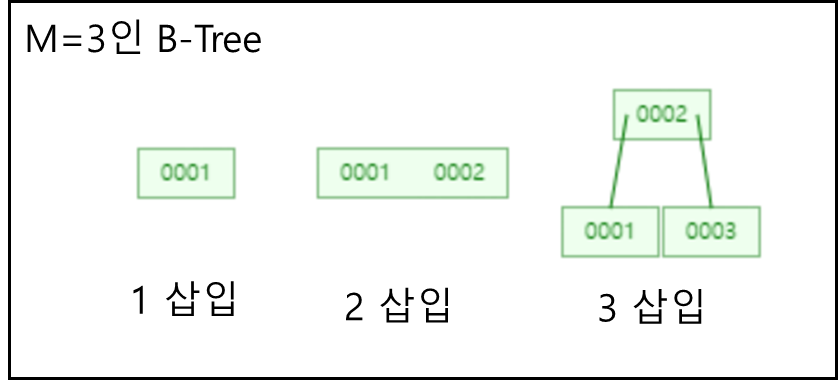
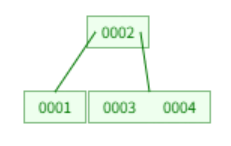
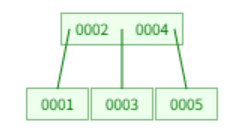
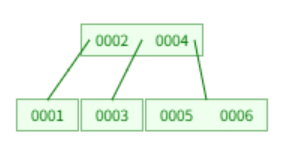
차수(노드가 가질 수 있는 자식 수)가 3일때 값 삽입하는 절차는 다음과 같다.
- 5 삽입시 최대 키 갯수를 초과하므로 트리 분할
- 6 삽입시 5 오른쪽으로 붙음
- 7 삽입시 5,6,7로 최대 키 갯수 초과하므로 중간값인 6을 상위 노드로 올리는데 그러면 2,4,6으로 역시 개수가 초과되어 중간 값인 4를 상위 노드로 올림
키 삭제 절차
값을 삭제하는 절차는 다음과 같다.
- 1,2,3,4,5,6,7로 이루어진 트리가 있다.
- 6을 삭제한다고 하면 6을 삭제하고 하위 노드중 작은 값을 그 자리로 올린다.
- 5에 자식 노드가 7 하나 달려있으므로 합친다.
- 5와 7의 상위 노드가 비므로 상위 노드에서 값을 갖고와서 부모로 삼는다.
- 2와 4가 root가 된다.
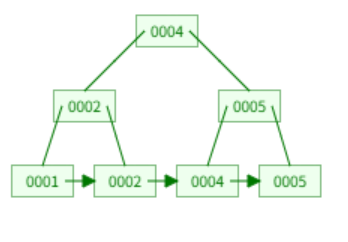
B+ Tree
기본적으로 B- Tree이나 다음과 같은 특징을 추가로 갖는다.
- B Tree의 경우 리프노드가 아닌 노드들이 key와 value를 전체 다 가지고 있을 수 있지만 B+ Tree의 경우 key만 갖고 있다.
- 리프 노드가 key와 value를 모두 갖고 있으며 각 리프노드는 링크로 연결되어있다.
- B Tree는 리프 노드에 중간 키가 없지만, B+ 트리는 중간 키가 있다.
- 이러한 구조로 인해 DB의 인덱싱 구현에 많이 사용한다.
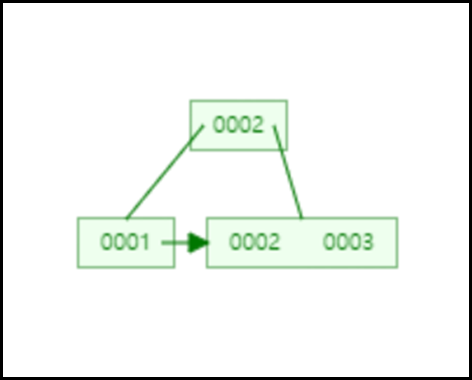
키 삽입 절차
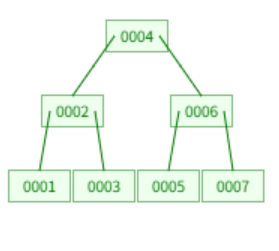
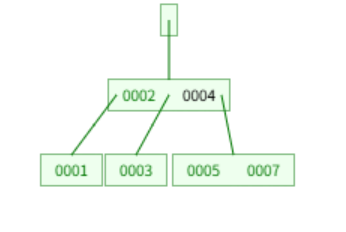
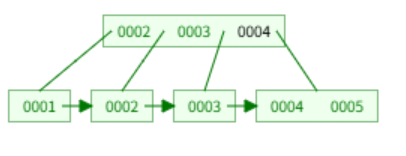
아래와 같이 기본 트리가 있다고 해보자.
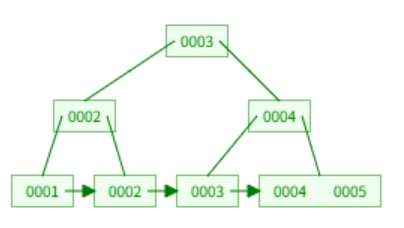
여기서 값으로 5를 넣는다고 할때 아래와 같이 변한다. 먼저 leaf node 중에서 맞는 위치에 넣는다. 여기서는 4 다음 위치이다.
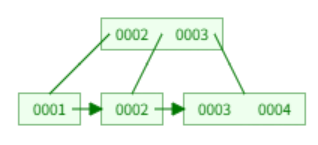
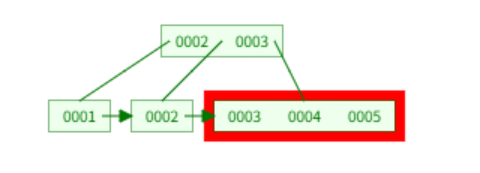
leaf node 값이 3개이므로 최대 키 값을 초과하므로 이를 분할한다.
이렇게되면 2,3,4로 3개가 되어 최대 키 값을 초과하므로 이 역시 분할해야한다.
중간에 있는 3을 루트 노드로 올리면 삽입이 완료된다.
키 삭제 절차
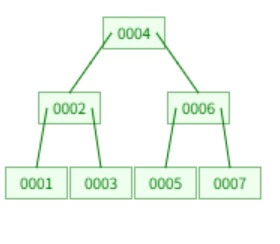
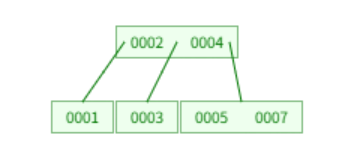
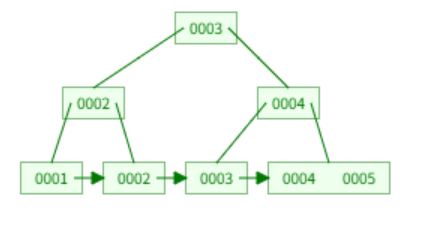
아래와 같은 트리가 있다고 해보자.
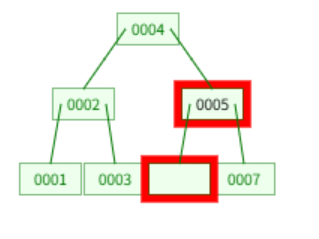
여기서 3을 제거하게되면 아래와 같은 절차를 거친다.
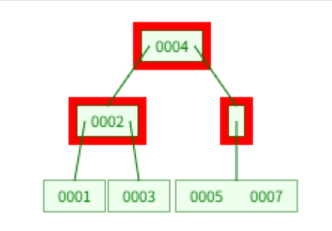
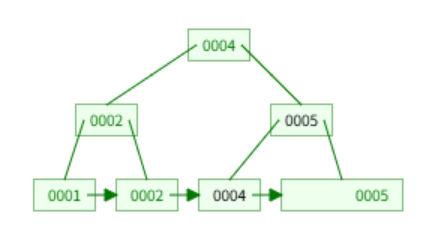
leaf node에서 3을 제거하고 root에서 3을 제거한다. 이후 4를 root로 올리고, 5를 root의 바로 아래로 올린다.
삭제가 완료되었다.
Red-Black Tree
자가 균형 이진 탐색 트리의 일종으로 세부적인 특징은 아래와 같다.
- 모든 노드는 검은색이거나 빨간색이다.
- 루트는 검은색이다.
- 모든 리프 노드들은 검은색이다. 여기서 리프노드란 데이터가 들어 있는 노드에 가상으로 붙어있는 NIL 노드들을 말한다.
- 빨간색 노드의 자식은 검은색이다.
- 모든 리프노드에서 루트까지 가는데 만나는 BLACK 노드의 갯수는 같다.
- 새로운 노드를 삽입할 때는 무조건 빨간색이다.
위 수칙들을 지키면서 노드를 삽입하게 되는데, 삽입시 4번째 법칙을 어기게되면 두 가지 방법으로 이런 문제를 해소하게 된다. 이 두 가지 중 어떤 것을 선택할 것이냐는 부모 노드의 형제 노드가 검은색이냐 빨간색이냐에 따라 달렸으며 해당 노드가 검은색 일 경우 Restructuring, 빨간색일 경우 Recoloring을 실행 한다.
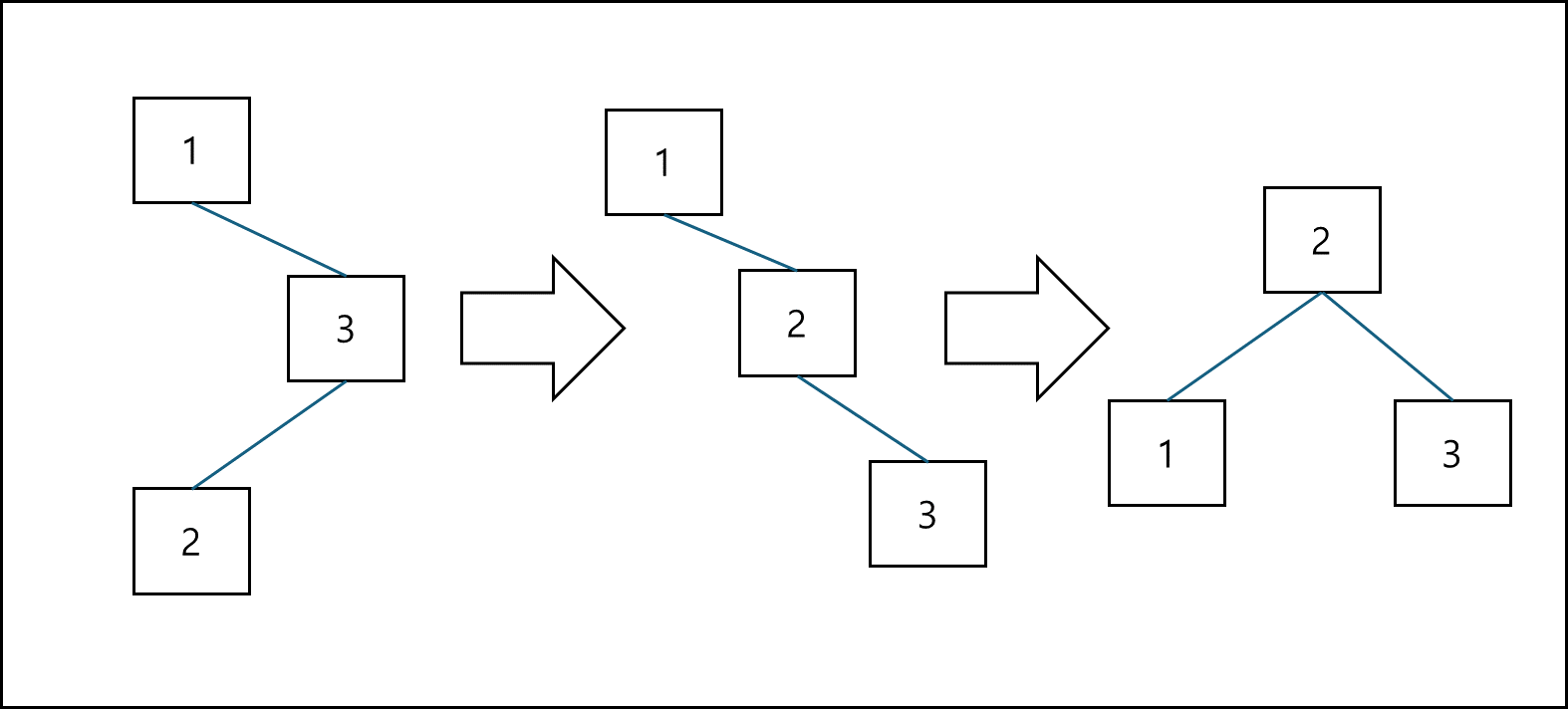
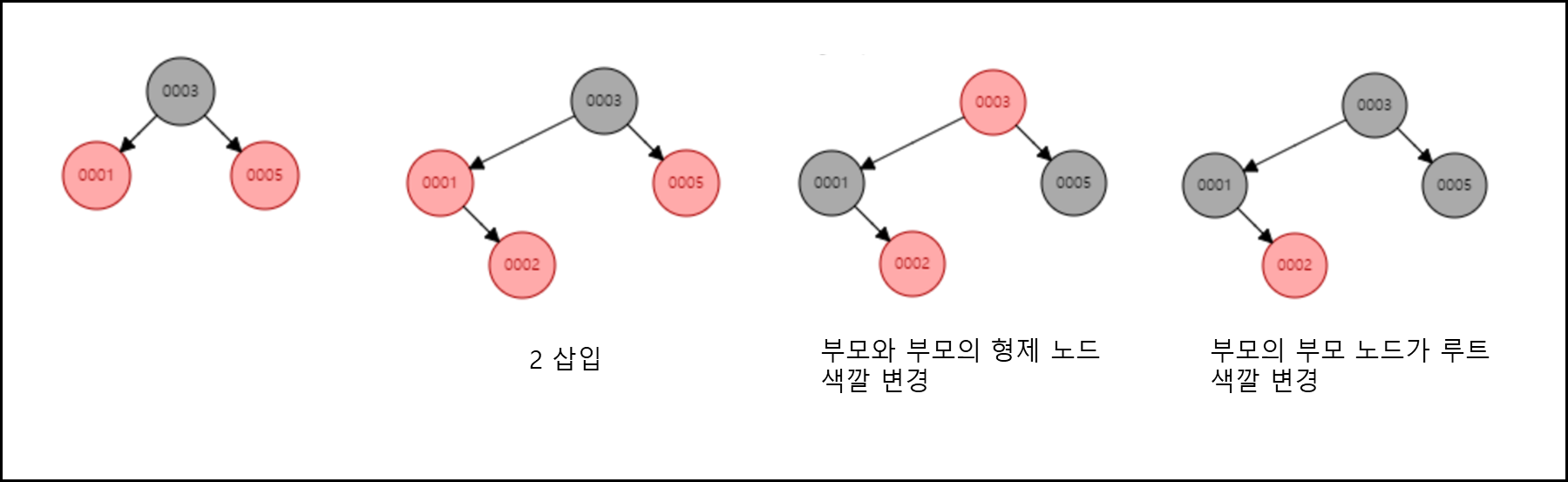
Restructuring
- 새로운 노드, 부모 노드, 부모의 부모 노드를 오름차순으로 정렬한다.
- 셋 중 중간값을 부모로 만들고 나머지 둘을 자식으로 만든다.
- 새로 부모가 된 노드를 검은색으로 만들고 나머지 자식들을 빨간색으로 만든다.
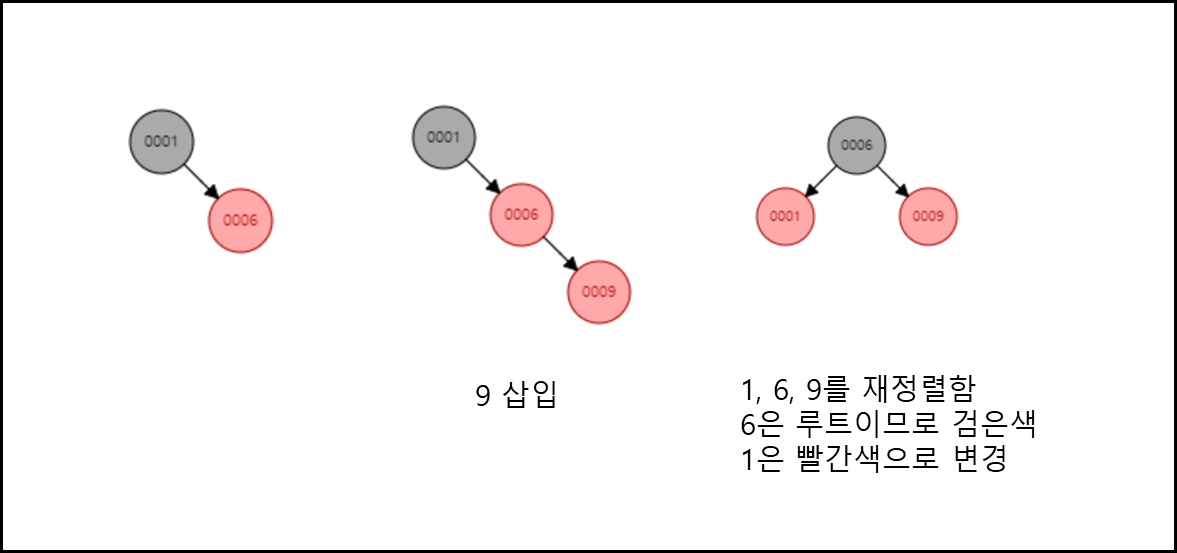
Recoloring
- 새로운 노드의 부모와 부모의 형제를 검은색으로 바꾸고 부모의 부모를 빨간색으로 바꾼다.
1-1. 부모의 부모가 루트 노드라면 검은색으로 바꾼다.
1-2. 부모의 부모가 빨간색으로 바꿨을 때 또다시 4번째 수칙을 어긴다면 또다시 Restructuring 혹은 Recoloring을 진행해서 해당 문제가 발생하지 않을 때까지 반복한다.
AVL Tree
기본적으로 이진 탐색 트리의 속성을 가지며 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1로 유지하는 속성을 가지고 있다. 이러한 균형을 유지하는데 Balance factor 값을 사용하며 각 노드가 값을 갖고 있는데 이 값을 산출하는 방법은 다음과 같다.
Balance Factor (k) = height (left(k)) - height(right(k))
- 1이면 왼쪽이 오른쪽보다 더 높다
- 0이면 왼쪽과 오른쪽이 같다
- -1이면 오른쪽이 왼쪽보다 높다.
만약 BF가 -1이나 0이나 1이 아닐 경우 불균형 상태로 보며 rotate 작업을 통해 균형을 유지하게 되는데 각각 LL, RR, LR, RL 네가지 형태의 rotate 경우가 있다.
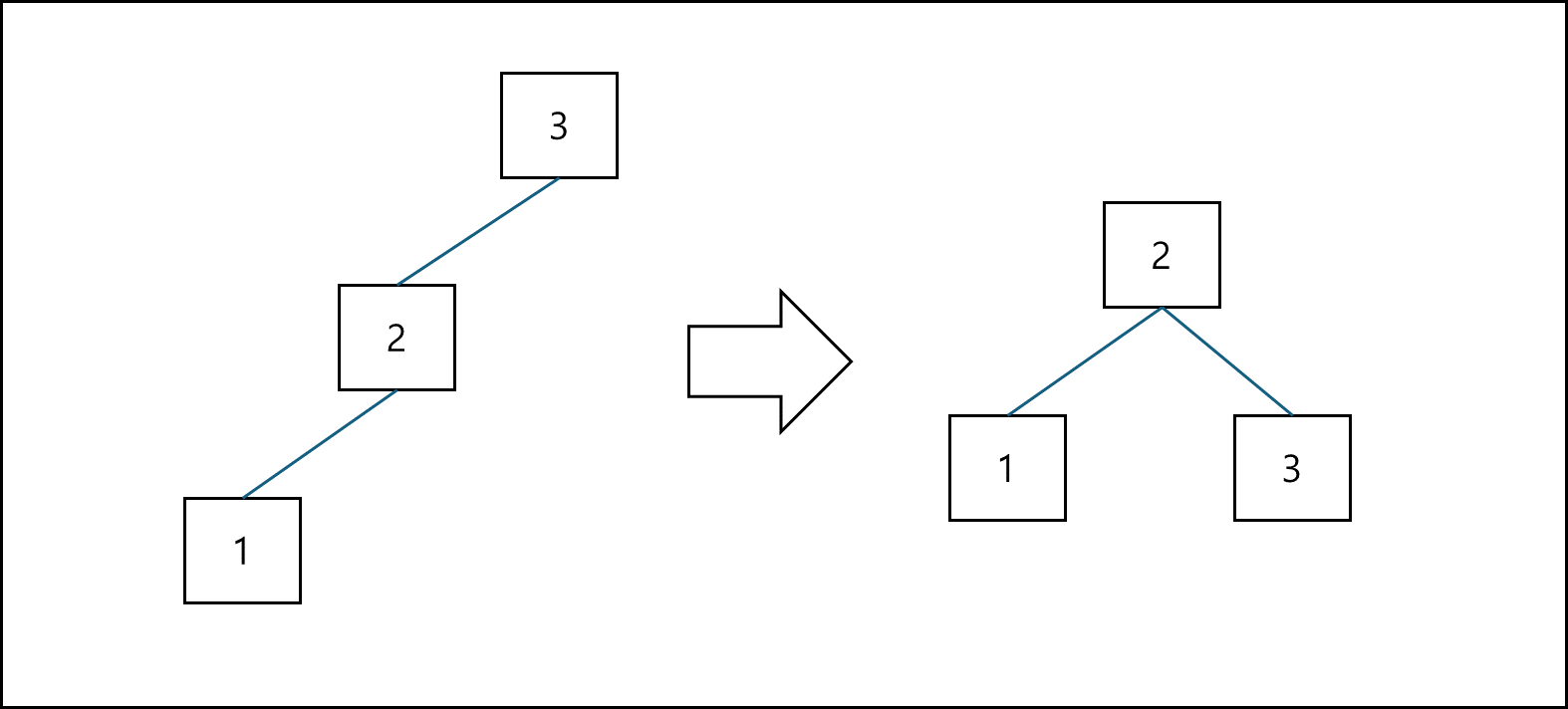
LL
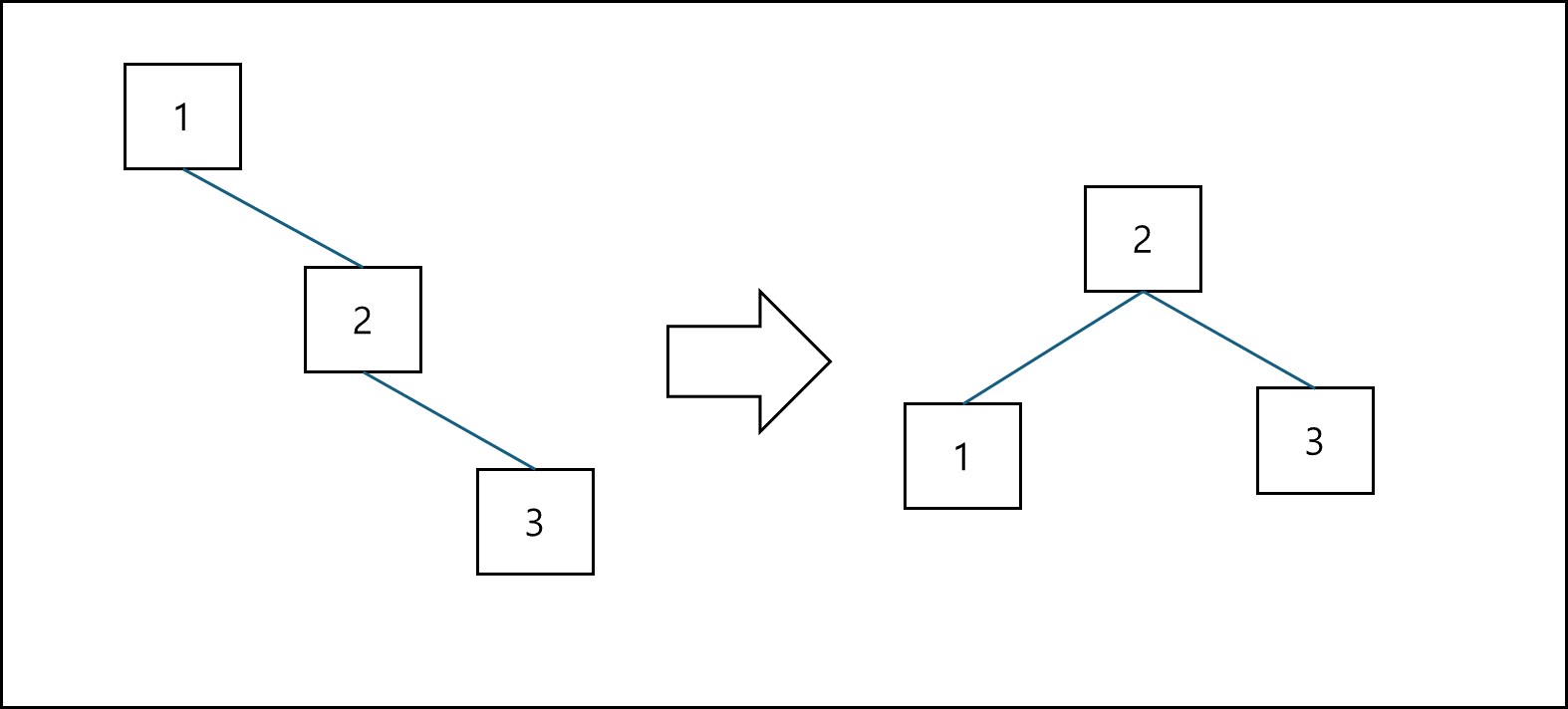
RR
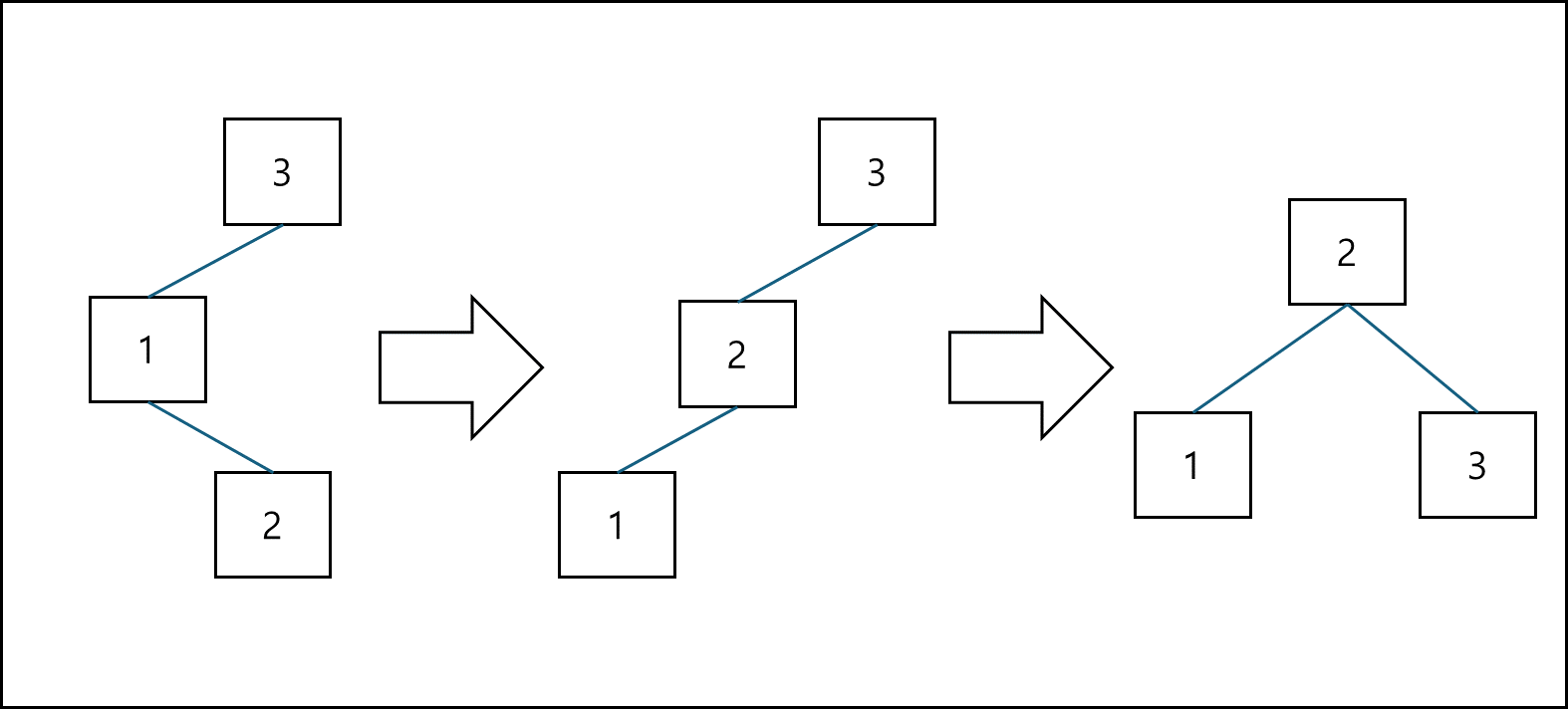
LR
RL
참고 자료
- 코드 연구소:티스토리
- yoongrammer
- Data Structure Visualizations
- 학부생 시절 강의 자료들