팀 정렬
팀 정렬(Tim sort)
개요
일반적으로 정렬 알고리즘 중에 평균적인 상황에서 가장 빠른 알고리즘은 힙 정렬, 병합 정렬, 퀵 정렬이라고 알고 있을 것이다. 이렇게 빠르다고 알려진 알고리즘을 사용할 때도 주의할 점이 있다.
먼저 최악의 상황에서의 성능이다. 퀵 정렬은 최악의 경우 O($N^{2}$)이다. 물론 메모리는 다른 정렬에 비해서 상대적으로 덜 사용하긴 최악의 상황에서 이렇게 느리다는건 문제가 있다.
두번째는 메모리 사용량이다. 병합 정렬은 평균과 최악의 상황에서는 준수한 상황을 보이나 메모리를 다른 정렬 알고리즘에 비해서 훨씬 많이 사용한다.
세번째는 지역 참조성이다. 이 지역 참조성이란 말은 캐싱에서 사용되는 말인데, 캐싱이란 이전에 사용했던 데이터를 잠시 가까운데 보관해두었다가 요청받으면 보관해둔 데이터를 내어주는 형식이다. (이러한 캐싱 데이터를 보관하고 보관된 데이터를 교체하는 정책에 대해서 말하자면 한도 끝도 없으니 적당히 이 정도만 설명하고 넘어가겠다)
병합정렬과, 퀵 정렬은 상대적으로 지역참조성을 잘 활용할 수 있는 방면에 힙 정렬은 그렇지 못하다. 따라서 캐싱의 성능을 잘 활용할 수 없다.
이렇게 정렬 알고리즘을 하나 사용하려면 고민해야할게 많다.
정렬 알고리즘에 대한 고민은 소프트웨어 엔지니어인 Tim Peters에게도 예외는 아니었다. 그는 참조 지역성의 원리를 잘 만족하고 안정적인 성능을 보장하는 정렬 알고리즘을 고심하다가 2002년 Tim sort라는 정렬 알고리즘을 고안해냈다.
(사실 이 팀 피터스라는 사람이 생각했다기엔 조금 말이 나올수가 있는게 이 사람도 Optimistic Sorting and Information Theoretic Complexity 라는 논문을 참고했다고 한다.)
이 알고리즘은 현재 버전 2.3부터 파이썬의 표준 정렬 알고리즘이다. 자바 SE 7, 안드로이드, GNU 옥타브, V8, 스위프트, 러스트에서 프리미티브가 아닌 타입의 배열을 정렬하는데 사용된다.
원리
기본적으로는 삽입 정렬 + 병합 정렬인 형태이다.
작은 개수에 대해서는 삽입정렬이 빠르다. 이것을 이용하여 각각 데이터 덩어리를 작은 덩어리로 자른 뒤 각각의 덩어리를 삽입정렬로 정렬 한 뒤 병합하면 빠르지 않을까 하는게 이 알고리즘의 주요 원리이다.
$2^{x}$개 씩 잘라 각각 삽입정렬로 정렬하면 일반적인 병합정렬보다 덩어리별로 x개의 병합 동작이 생랴된다. 이때 병합정렬의 동작 시간을 $C_{m} \times nlog n$이라 할때 팀 정렬의 동작시간은 $C_{m} \times n(log n -x)+\alpha$가 된다. 이때 x 값을 최대한 크게하고 $\alpha$를 줄이기 위해 여러가지 최적화 기법이 사용되는데 그 기법은 아래와 같다.
최적화 기법 종류
Run
$2^{x}$개씩 잘라 각각 삽입정렬로 정렬하는데 일정 이후에는 삽입정렬로 정렬하지 않고 덩어리를 크게 키워서 병합 횟수를 줄이는 방식이다.
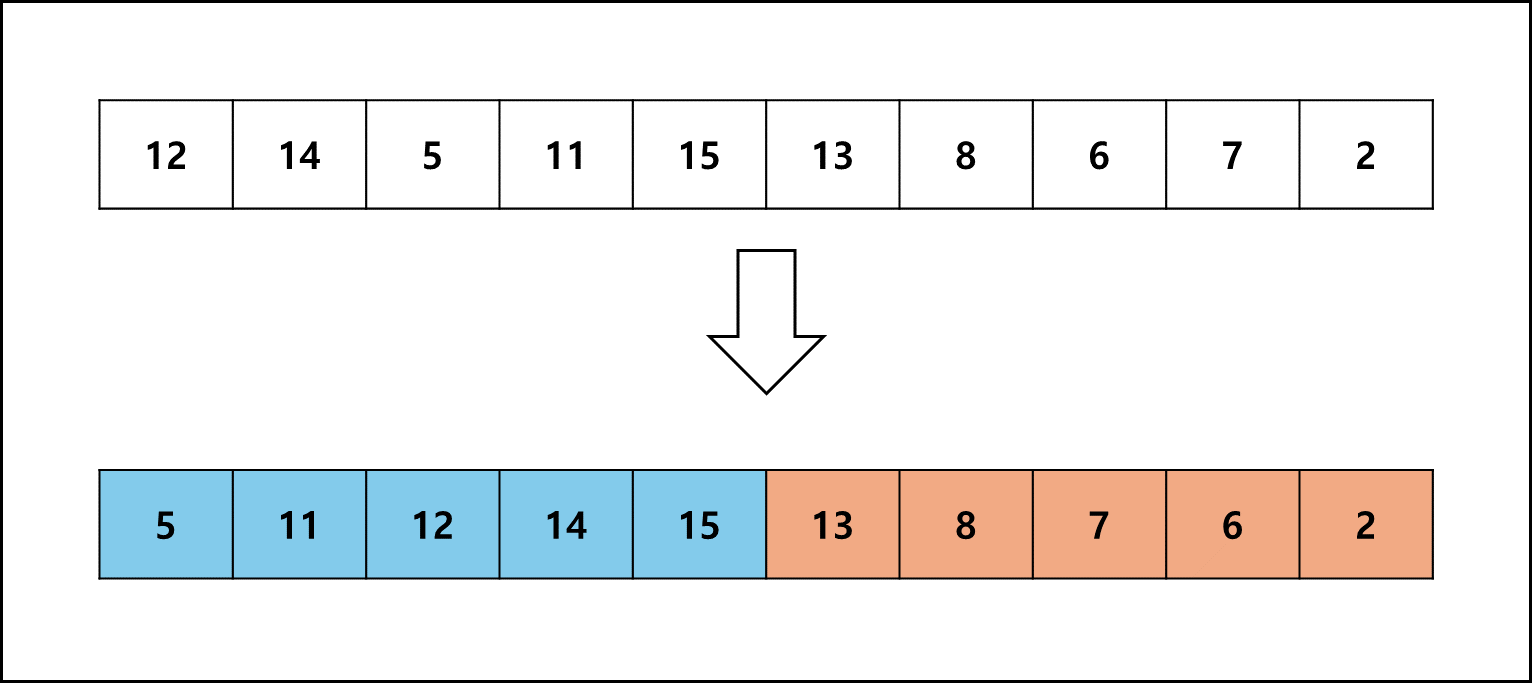
위 그림의 배열에서 $2^{2}$개씩 나눈다고 가정하면 일단 앞의 4개까지는 삽입정렬로 정렬한다. 그러면 [5,11,12,14]가 된다. 덩어리가 크면 클수록 병합 횟수를 줄일 수 있으므로 이미 정렬된 덩어리를 키울 수 있다면 키우는데, 바로 그 다음 숫자가 이미 정렬된 숫자의 가장 큰 수보다 크다면 정렬된 덩어리에 붙이는 방식으로 덩어리를 키운다. 따라서 뒤에 바로 붙은 숫자는 이전에 정렬된 배열의 가장 큰수보다 크므로 정렬된 덩어리에 붙여서 [5,11,12,14,15]로 만들어준다.
그 다음 숫자부터는 작아지므로 새로운 덩어리를 만드는데 이 덩어리는 감소하는 방향으로 덩어리를 만든다. 그래서 [13,8,7,6]까지 정렬한다. 방금 만든 덩어리는 감소하는 방향으로 만든 덩어리이고, 덩어리 이후의 데이터가 2라 6보다 작으므로 덩어리에 붙여서 [13,8,7,6,2]로 만들어준다. 이후에 이렇게 감소하는 형태의 덩어리는 뒤집어서 증가하는 run이 되도록 변환한다.
이렇게 정렬 후 끝 원소의 대소만 비교하여 덩어리를 만든 것을 run이라고 하며 이때 $2^{x}$를 minrun이라 한다. 이미 정렬된 배열에서 하나의 run만 생성되고 삽입 정렬로 정렬되기 때문에 최선의 시간복잡도가 $O(n)$이 되는것이다.
증가하는 run은 다음 데이터가 이전 데이터의 이상일때, 감소하는 run은 다음 데이터가 이전 데이터 크기의 미만일때를 두고 만든다.
팀 정렬은 전체 원소 개수를 N이라 할때 minrun의 크기를 N과 $2^{5} ~ 2^{6}$ 중에 작은 값을 취하는데 고정 된 값으로 정할 경우 느려지는 경우가 있기 때문이다.
Binary Insertion sort
팀정렬에서 사용하는 사용하는 삽입 정렬은 이진 삽입 정렬로, 삽입 위치를 찾을때 이진 탐색을 진행하여 위치를 찾는 방식이다.
물론 데이터를 밀어넣으면 다른 데이터를 옮기는데 시간이 걸리지만 나머지 원소를 시프트하는 연산 자체는 그렇게 느리지 않기 때문에 효율적이다.
Stack을 이용한 Merge
효율적인 방법으로 run 들을 병합하기 위한 방식이다. 병합시 병합하려는 run의 크기가 비슷하면 효율적이다. 따라서 이러한 run들을 몇개 합쳐서 최대한 크기를 맞춘 뒤 병합해주면 훨씬 효율적인데 이때 stack을 이용하여 작은 run들을 합쳐주게 된다.
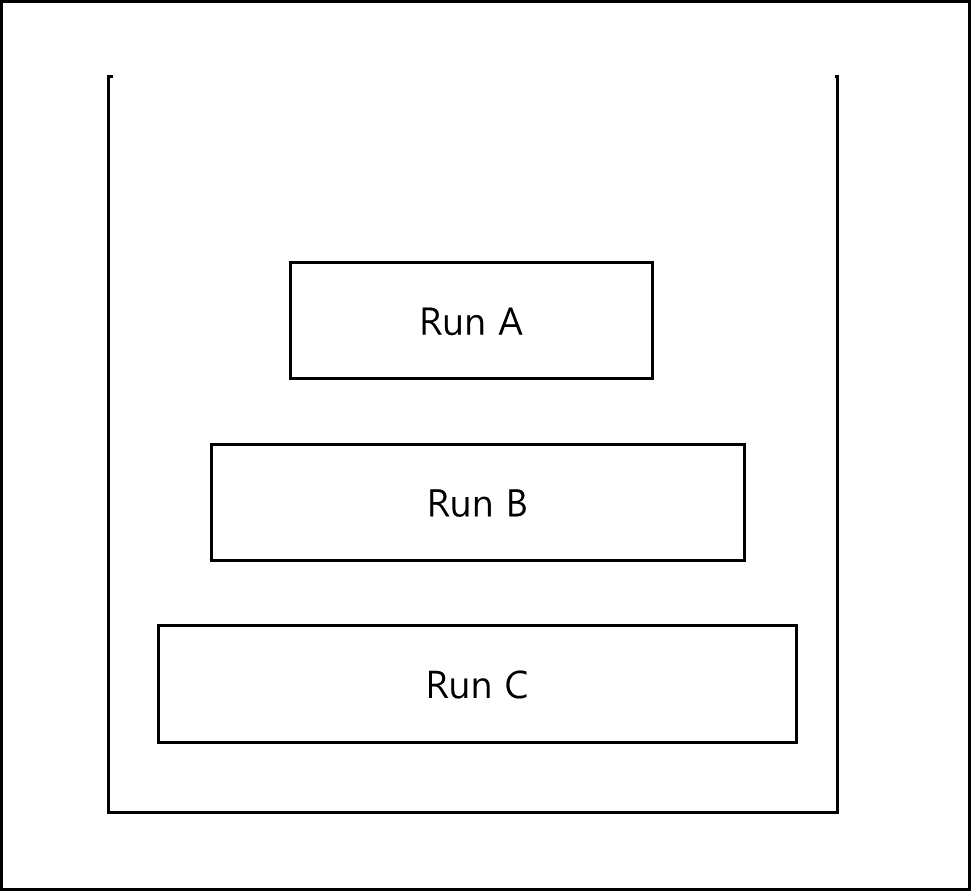
기본적인 원래는 높은 위치에 있는 것은 낮은 위치에 있는 것보다 무조건 작거나 같은 크기의 run으로 유지시켜주면 된다.
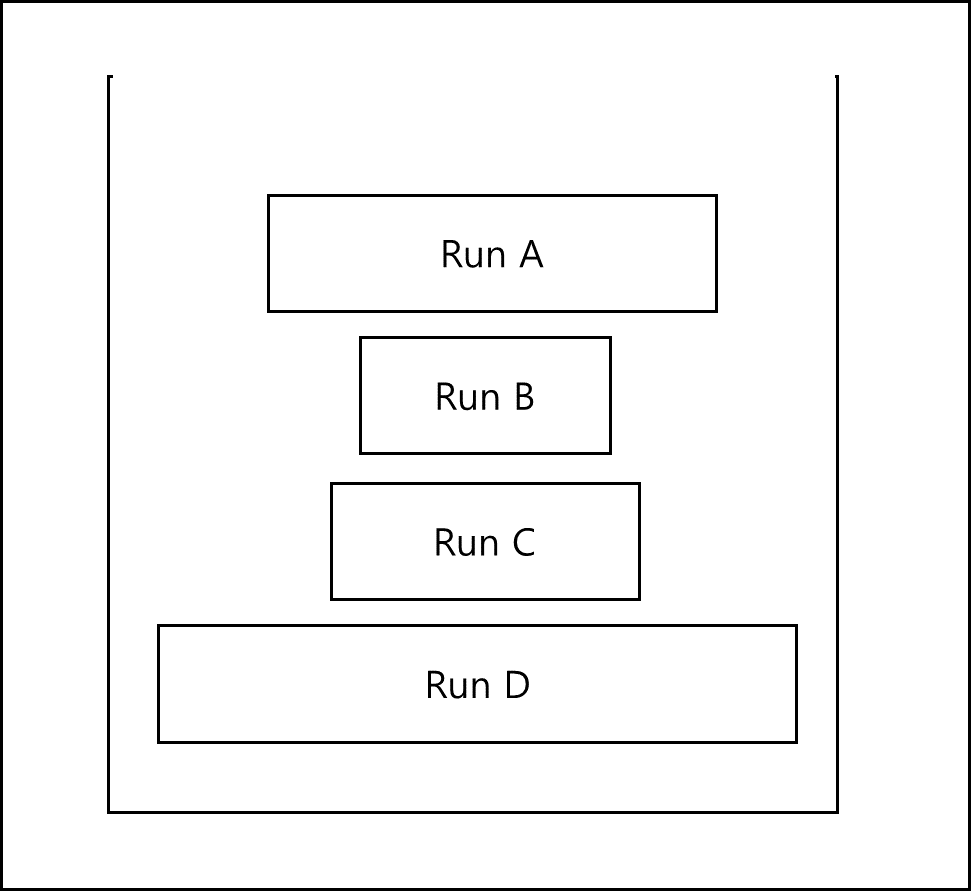
만약 다음과 같은 형태가 된다면 어떻게 할까?
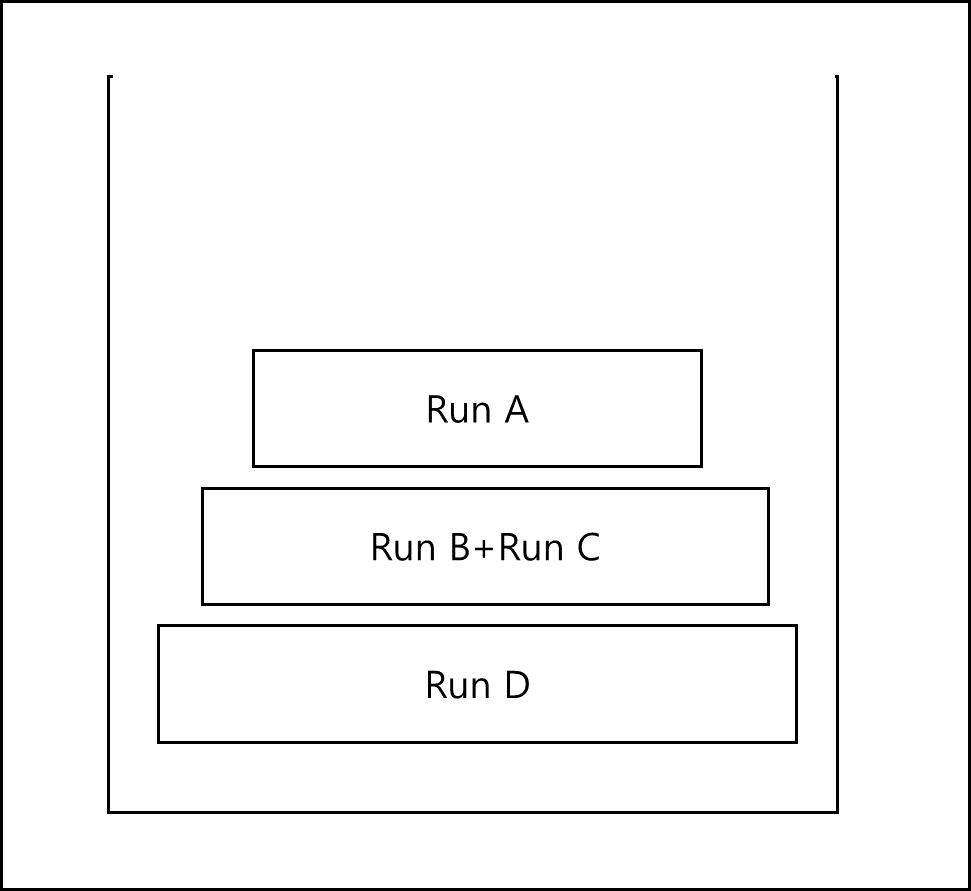
그러면 중간의 run 중에 크기 비슷한 run을 합쳐서 사이즈를 맞춰준다.
2 Run Merge
사이즈를 비슷하게 맞춘 Run을 합치는 것은 좋은데 병합 정렬은 특성상 추가적인 메모리를 요한다. 팀 정렬에서는 이러한 메모리 사용량을 최소로 줄이고자 다음과 같은 방법을 사용한다.
- 병합 대상 Run 두 개의 각각 크기를 비교한다.
- 작은 크기의 Run을 복사해서 별도의 메모리에 갖고 있는다
- 작은 크기의 Run을 비교해가며 원래 배열에 합친다.
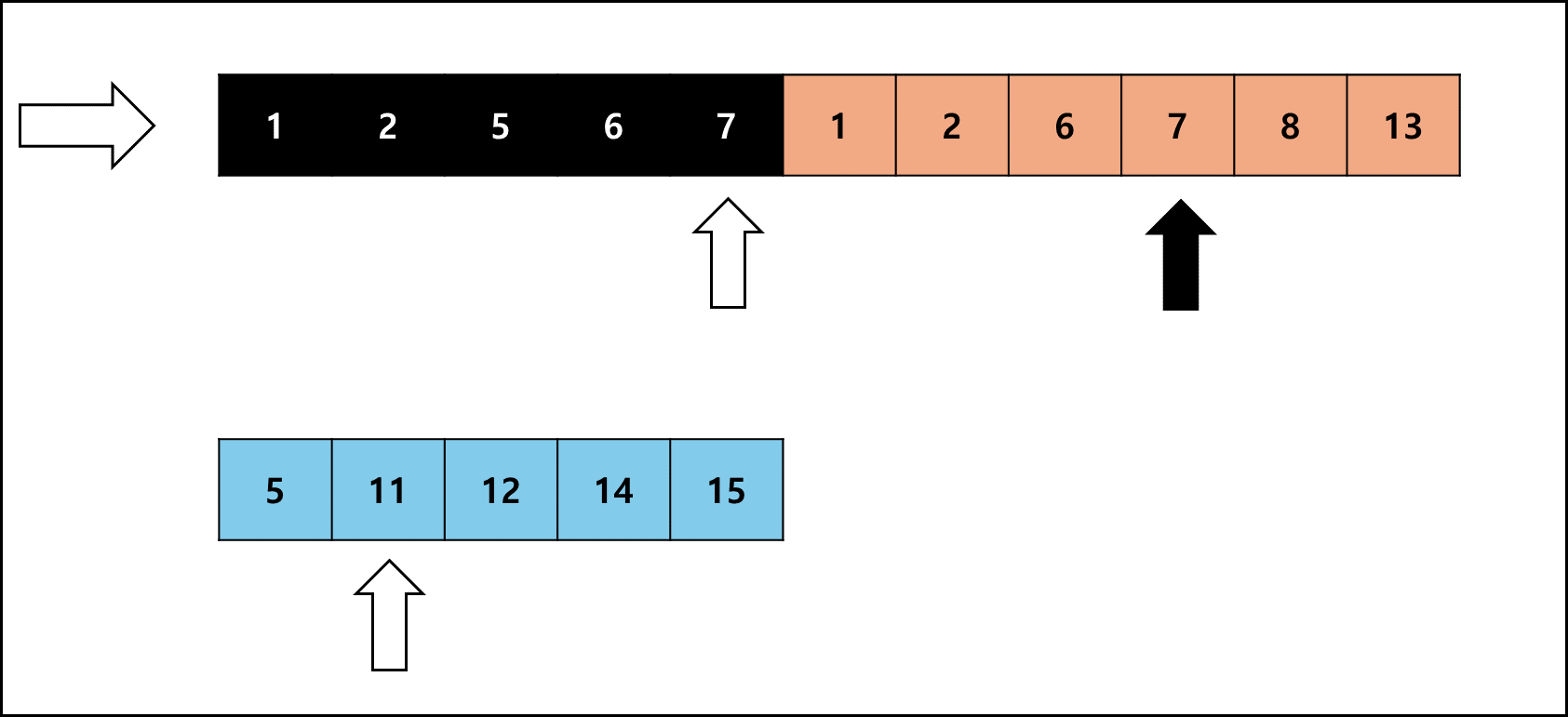
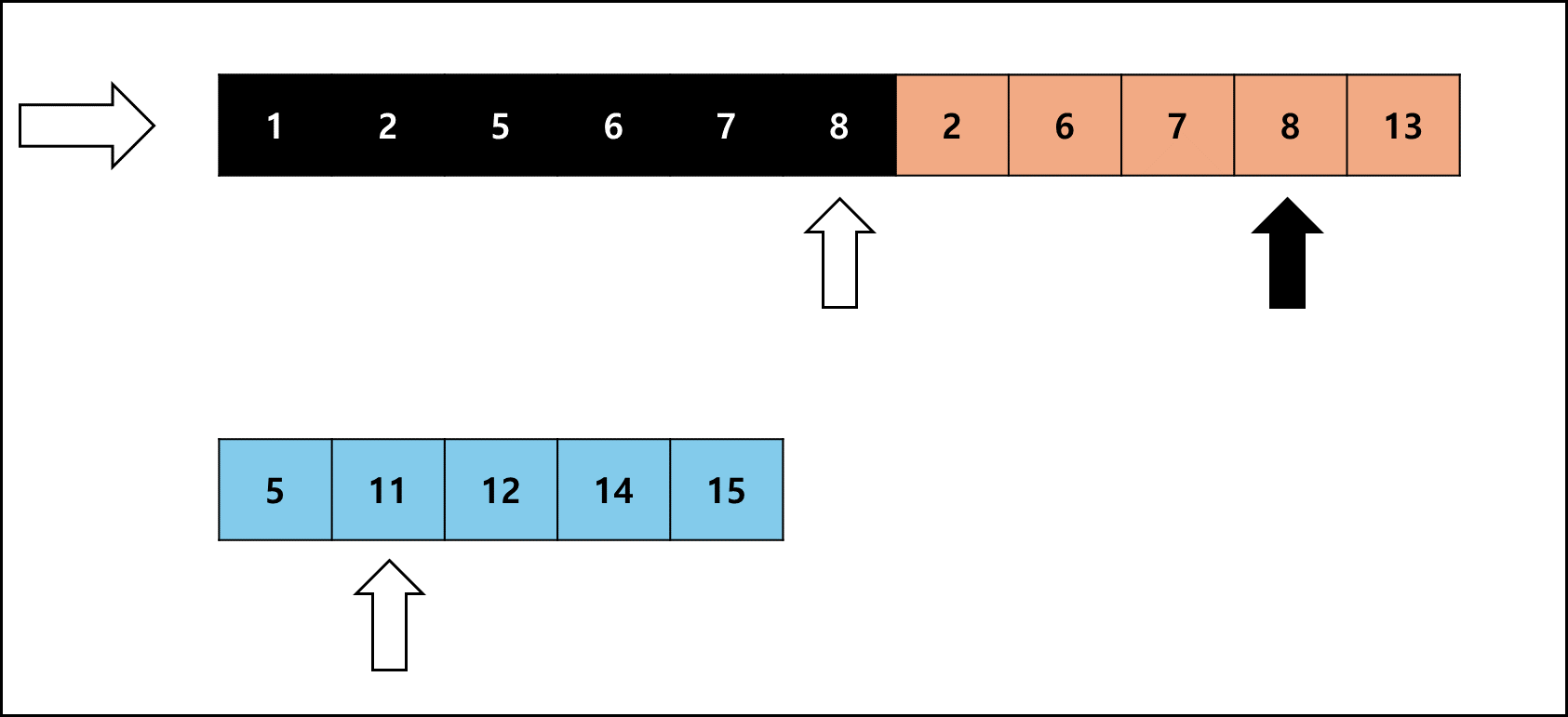
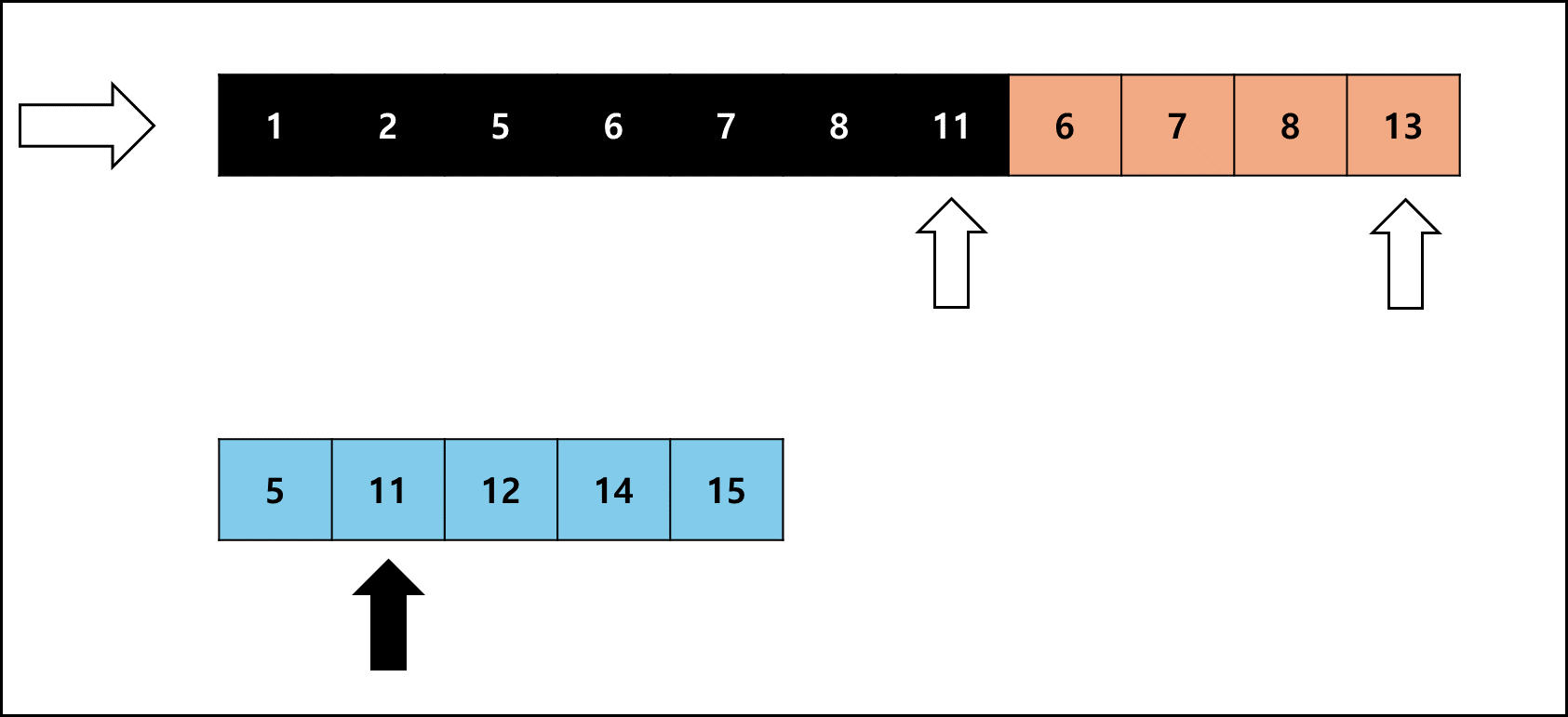
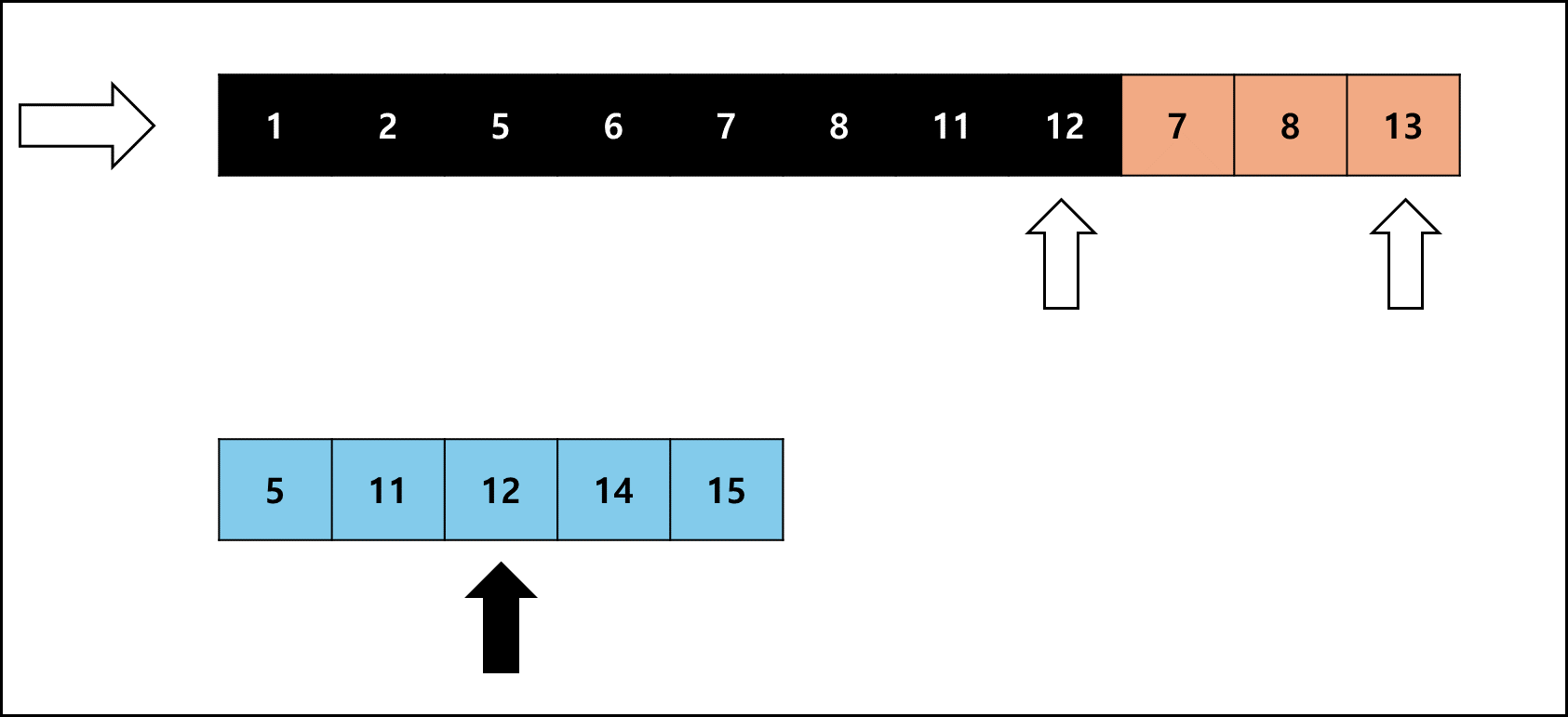
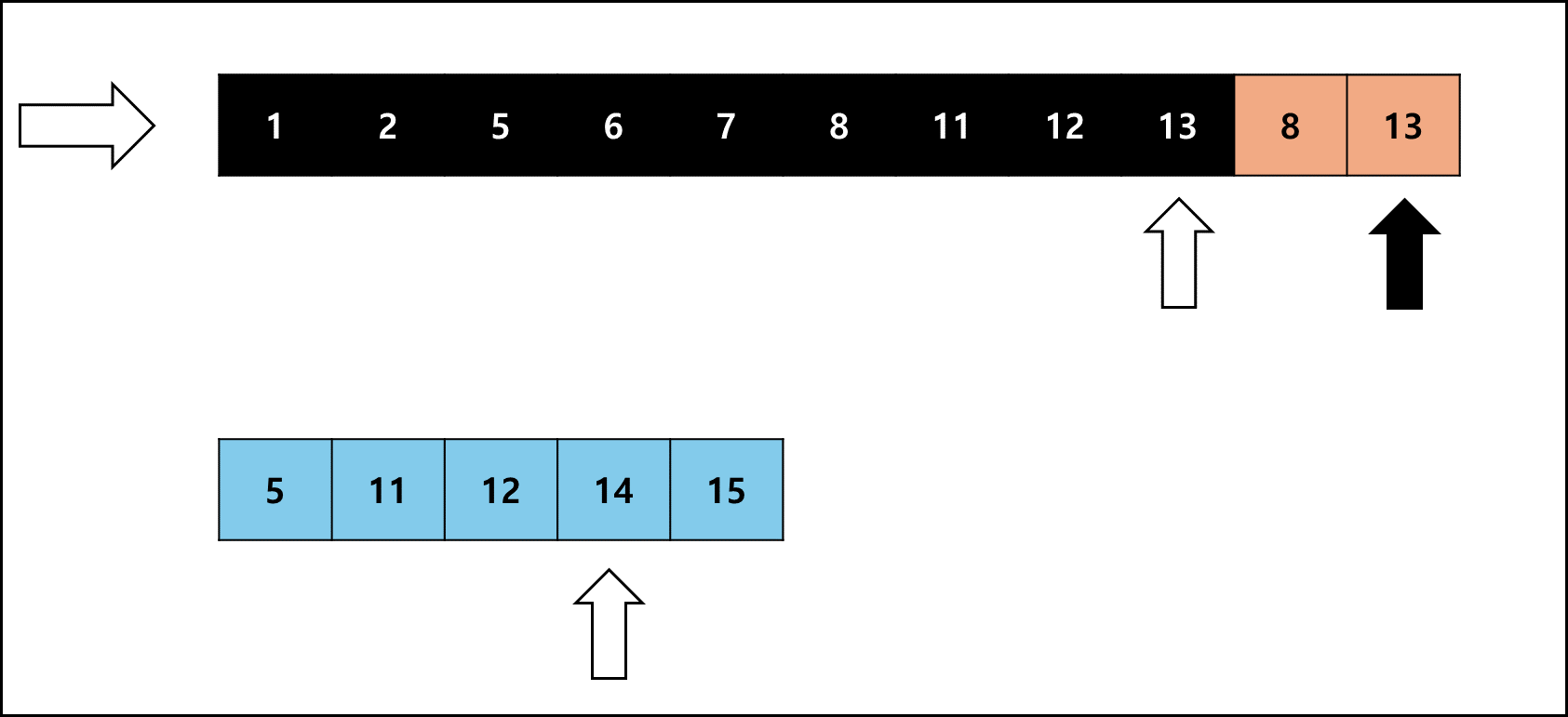
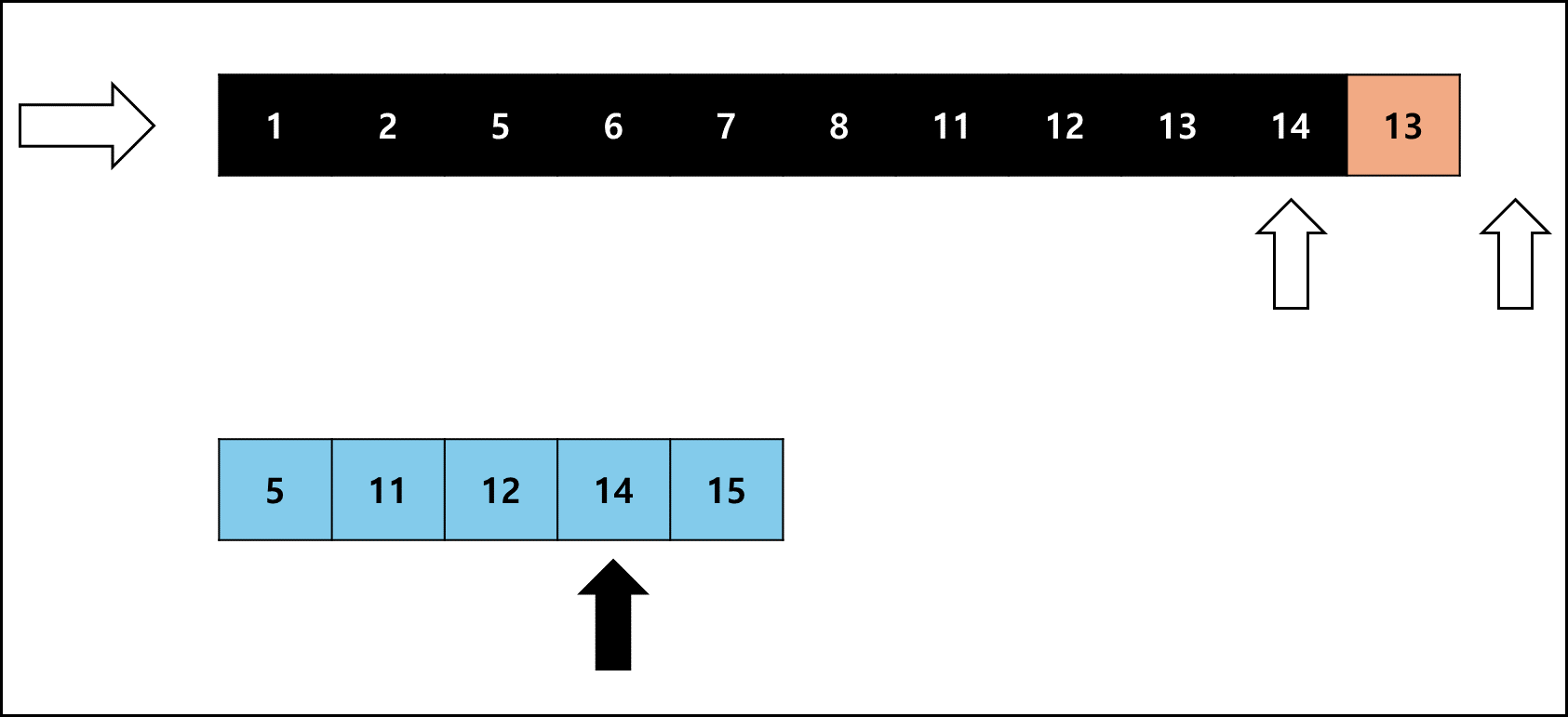
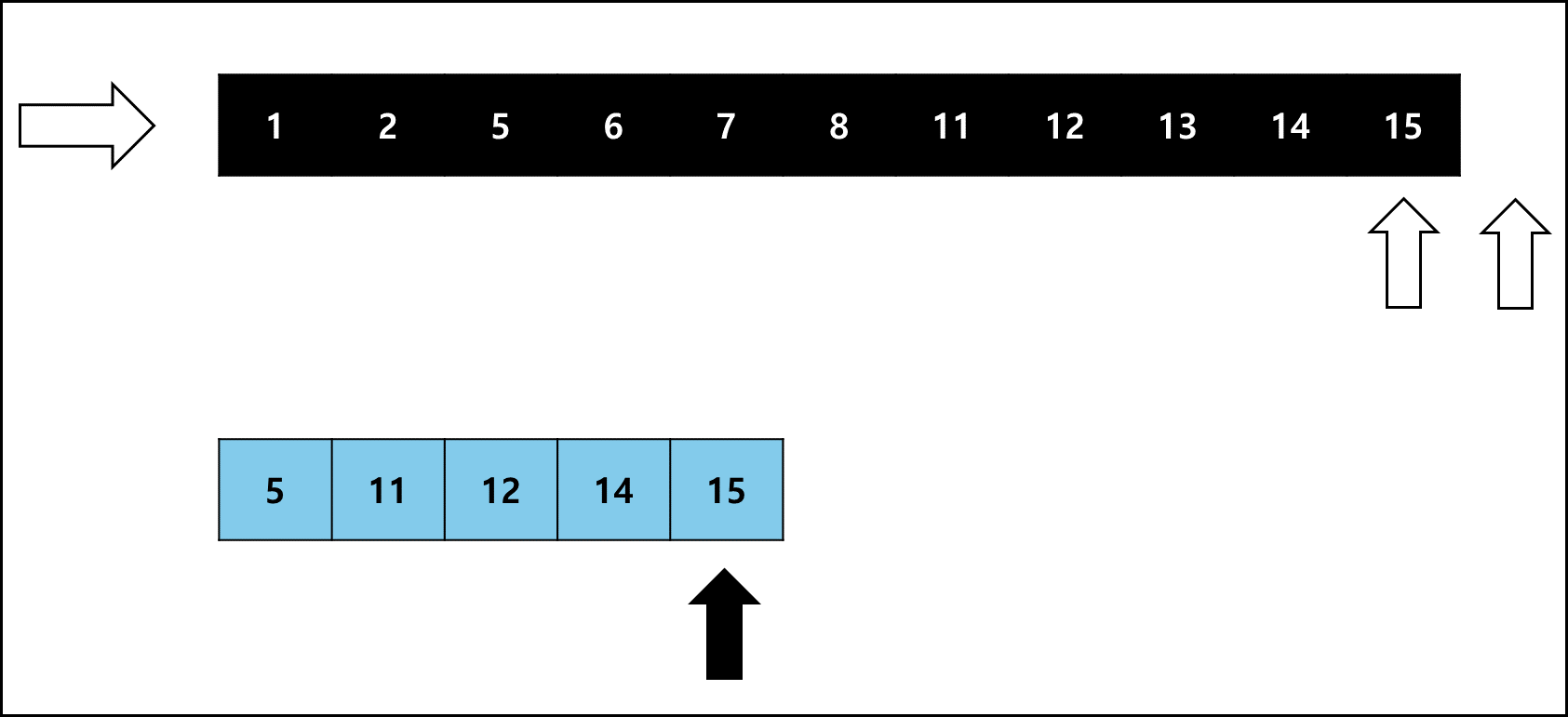
여기서 좌측 Run이 작다면 오른쪽으로 하나씩 비교하고, 우측 Run이 작다면 왼쪽으로 하나씩 비교하며 병합한다.
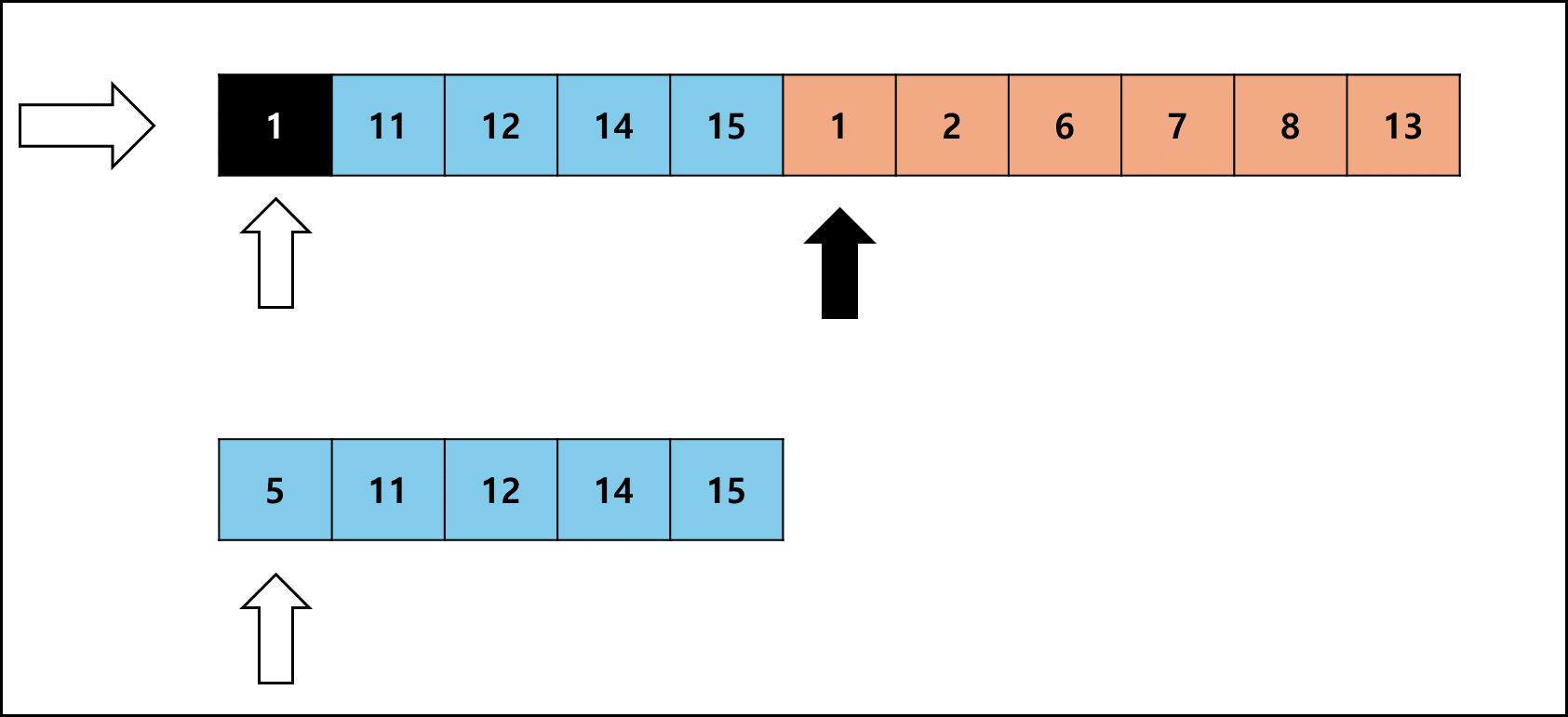
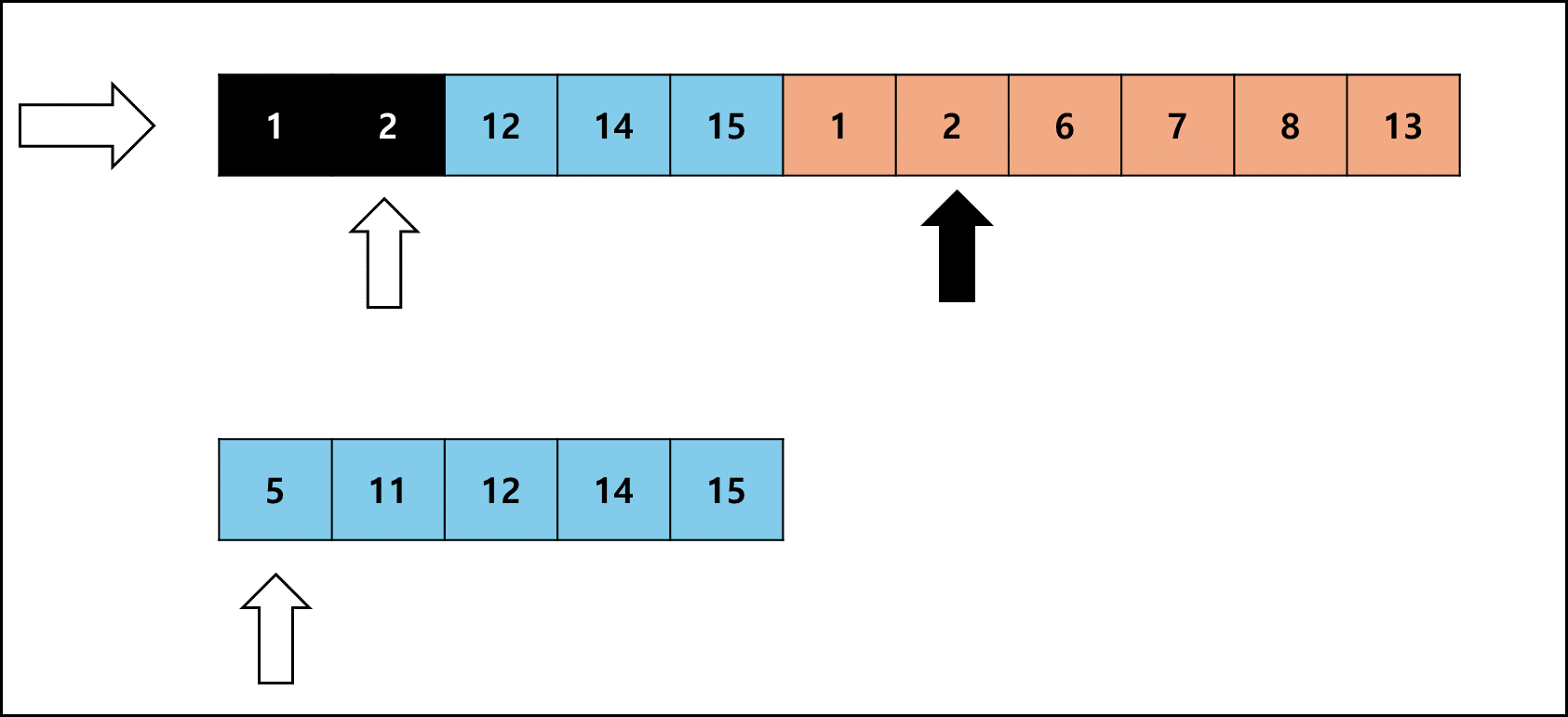
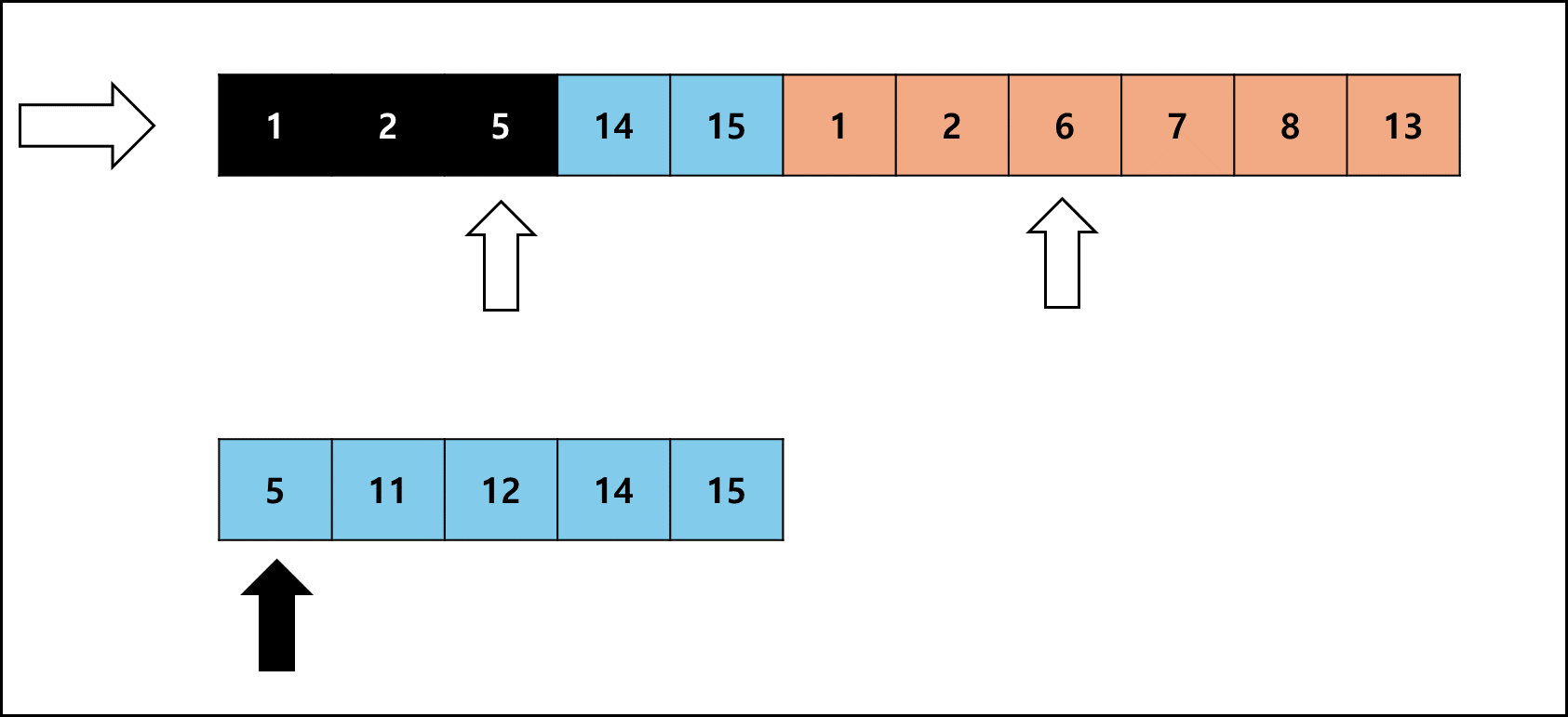
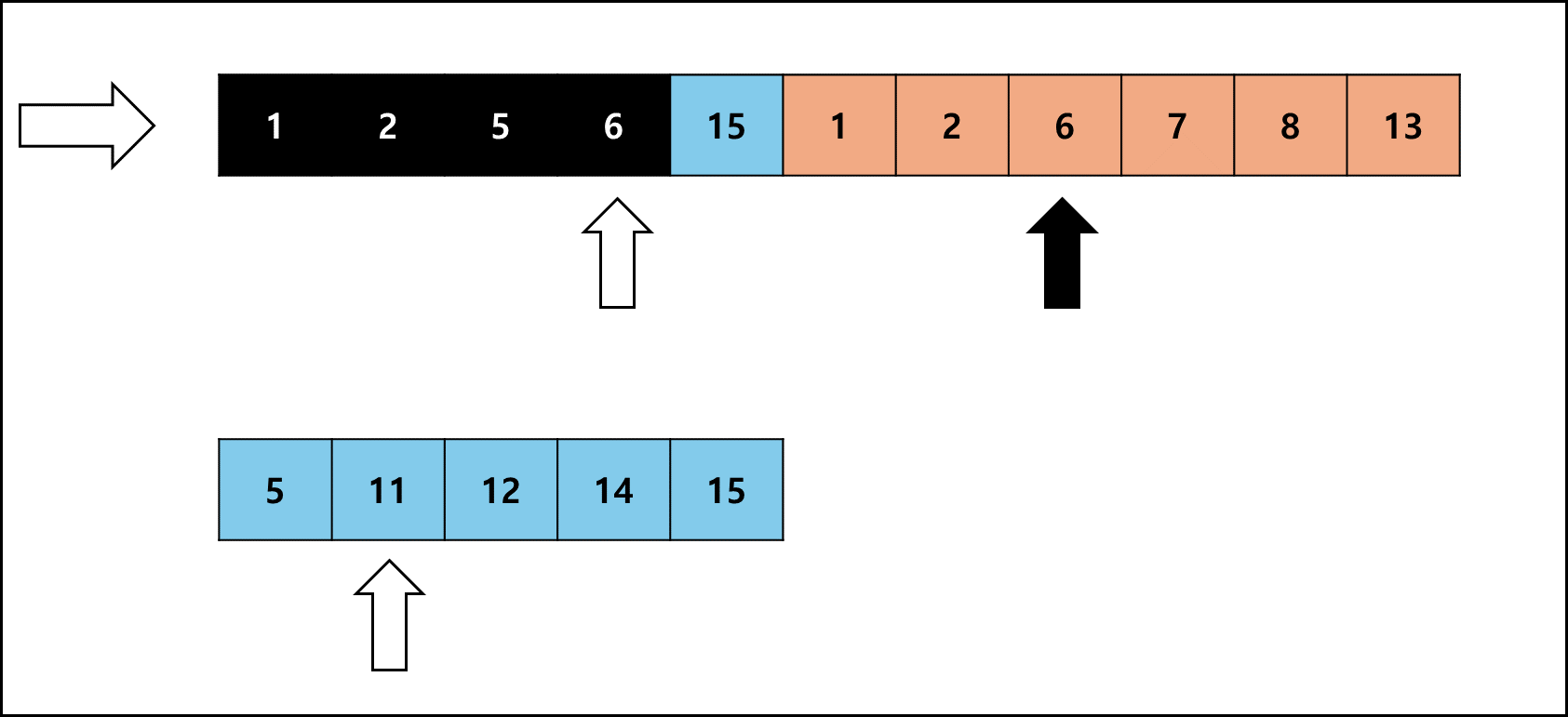
좌측 Run의 크기가 작을 때를 예시로 들면 아래와 같다.
Galloping
병합하는 과정에서 사용하는 방식으로 두 개의 run을 병합할때 두 원소를 대소 비교하게 되는데 순차적으로 인덱스를 1씩 늘려서 찾으면 느릴 수 있기 때문에 3번 연속 한 run의 원소를 사용하여 병합하게된다면. Galloping mode(질주 모드)를 이용하여 1,2,4,8과 같이 2의 승수 개수로 뛰어넘게 된다.
그러다가 대상을 넘게 된다면 이진 탐색을 통해 원래 대상을 찾아간다.