함수
1. 함수
(1) 함수의 정의
① 함수 (Function)
다음을 만족하는 X에서 Y로의 관계
$f : X \to Y$ 에서
ⓐ 모든 x에 대하여 y가 있어야한다.
\(\forall x \in X, \exists y \in Y, s.t. (x,y)\in f\)
ⓑ 같은 input에 대해선 같은 output이 나와야한다.
\((x,y_{1}) \in f \wedge (x,y_{2}) \in f \Rightarrow y_{1} = y_{2}\)
※ $(x,y) \in f$ 는 $y=f(x)$로도 쓴다.
위 조건에 맞지 않는 함수도 있으나 엄밀한 함수는 위 두 조건을 따름
함수 $f : X \to Y$에서 y=f(x)일 때
1) y를 f에 의한 x의 상
2) x를 f에 의한 y의 원상
3) X를 f의 정의역 Dom(f)
4) Y를 f의 공역
5) \(\left\{ f(x)| x\in X \right\} = f(X)\) 를 f의 치역이라 하며 Rng(f)라고 표기한다.
※ 함수 $f : X \to Y$에 대하여 $A\subset X$일 때,
② $f|_{A}$는 X를 A로 축소한 함수
\(\left\{ (x,y)\in f | x \in A \right\}\)
※ 축소한 함수란, 동일한 함수에 정의역만 줄어든 함수를 뜻함, 동일한 함수라고 정의역이 다르면 다른 함수로 취급한다. 확대한 함수는 축소한 함수의 반대.
③ $g=f|_{A}$이면 f는 g의 A에서의 확대 함수
(2) 함수의 성질
함수 $f : X \to Y$에 대하여
① 전사
치역과 공역이 같은 것 즉, Rng(f)= Y
② 단사
input 값이 다르면 output 값이 달라야함. 즉, $x_{1} \neq x_{2} \in X \Rightarrow f(x_{1}) \neq f(x_{2})$
③ 전단사
전사이고 단사인 함수, 일대일대응
(3) 여러 가지 함수
① 고등학교 교육과정 내
1) 항등함수
입력한 값이 동일하게 출력되는 것. 즉, $\forall x \in X, I_{X}(x)=x$
2) 상수함수
어떤 값을 넣어도 동일한 값이 출력되는 것. 즉, $\exists y_{0}\in Y, f(X)=y_{0}$
3) 역함수
전단사인 $f : X \to Y$에 대해 $f^{-1} : Y \to X$
4) 합성함수
두 함수 $f : X \to Y, g: Y \to Z$ 와 $\forall x \in X, (g \circ f)(x)=g(f(x))$
※ 합성 함수의 성질
- $g \circ f \neq f \circ g$
- $(h \circ g) \circ f = h \circ (g \circ f)$
- $f^{-1} \circ f = I_{x}$
- $f \circ f^{-1} = I_{y}$
- f,g가 모두 단사이면 $g \circ f$는 단사
- f,g가 모두 전사이면 $g \circ f$는 전사
② 고등학교 교육과정 외
집합 $A(\neq \varnothing )$ 가 $A \subset X$ 일때
1) 포함함수 (inclusion function)
항등 함수의 축소된 함수로 생각하면 편한데, 정의역이 X가 아닌 축소된 정의역인 A에서 공역이 X인 함수로 향하는 함수다. 식으로 나타내면 아래와 같다.
$\forall x \in A, i:A \to X$가 $i(x) = x (\in A) = I_{x}|_{A}$
2) 특성함수 (indicator function)
특정 값이 해당 집합에 포함되는지 안되는지 나타내는 함수로, 포함되어있다면 1로 포함되어있지 않다면 0으로 결과가 나온다. 식으로 나타내면 아래와 같다.
\(\forall x \in X, x_{A}: X \to \left\{ 0,1 \right\}\)가 \(x_{A}(x) = \left\{\begin{matrix} 1\; x\in A \\ 0\; x\notin A \end{matrix}\right.\)
3) 선택함수 (choice function)
집합 $X (\neq \varnothing )$의 부분 집합들의 집합족을 \(\left\{ A_{i} \right\}\) 이라 할때 모든 $i\in I$에 대하여 $f(A_{i})\in A_{i}$로 정의되는 함수 \(f: \left\{ A_{i} \right\} \to X\)
(4) 여러 가지 정리
1) 함수 F 에 대하여 역함수 $f^{-1}$가 존재하면 f는 전단사이다.
2) 함성함수 $g \circ f$가 단사이면 f는 단사이고, $g \circ f$가 전사이면 g는 전사이다.
3) 정수집합 Z와 자연수집합 N사이에는 일대일 대응이 존재한다, 즉 전단사 함수가 존재한다.
2. 집합의 함수
(1) 개념과 정의
함수 $f : X \to Y$에서 $A \subset X$이고 $B \subset Y$일 때 다음이 성립한다.
1) f에 대한 A의 상
\(f(A) = \left\{ f(x) \in Y | x \in A \right\}\)
2) f에 의한 B의 역상
\(f^{-1}B = \left\{ x \in X | f(x) \in B \right\} \subset X\)
위의 내용을 예를 들어 설명하자면
ex) f : IR -> IR가 $f(x) = x^{2}$이라 할때
A = {-1,0,1,2} => f(A) = {0,1,4}
B = {0,1,4} => $f^{-1}(B) = {-2,-1,0,1,2}$ 이다
일반적으로 상으로 보내진 집합은 작아지며, 역상으로 보내질 경우 집합이 커진다.
(2) 여러 가지 정리
함수 $f : X \to Y$에서 $A \subset X$이고 $B\subset Y$일 때 다음이 성립한다.
1) $f(\varnothing ) = \varnothing $
2) \(\forall x \in X, f(\left\{ x \right\}) = \left\{ f(x) \right\}\)
3) $f^{-1}(f(A)) = A \Leftrightarrow f$는 단사
4) $f(f^{-1}(B)) = B \Leftrightarrow f$는 전사
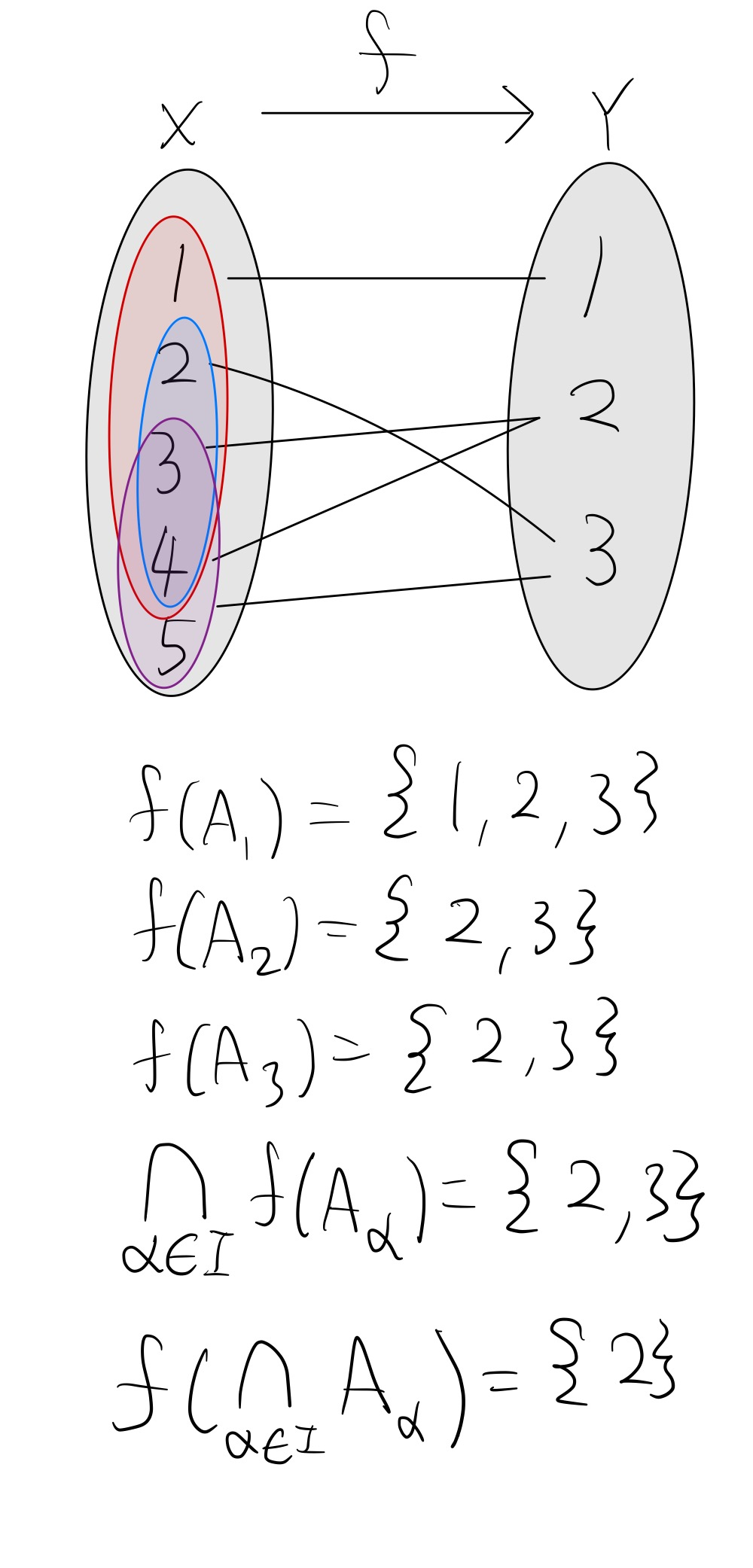
함수 $f : X \to Y$에 대하여 \(\left\{ A_{\alpha} | \alpha \in I \right\}\)를 X의 부분집합족이라하면 다음이 성립한다.
1) $f(\bigcup_{\alpha \in I}^{}A_{\alpha }) = \bigcup_{a\in I}^{}f(A_{\alpha })$
2) $f(\bigcap_{\alpha \in I}^{}A_{\alpha }) \subseteq \bigcap_{a\in I}^{}f(A_{\alpha })$
예시를 들면 아래와 같다.
3) f가 단사이면 $f(\bigcap_{\alpha \in I}^{}A_{\alpha }) = \bigcap_{a\in I}^{}f(A_{\alpha })$