힙
힙(Heap)
이전에 포스팅했던 완전 이진 트리(Complete Binary Tree)의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다. 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다. 큰값이 위에 오는지 작은 값이 위에 오는지 종류에 따라 최대 힙과 최소 힙으로 나눈다. 힙 트리에서는 중복된 값을 허용되는데 이는 이진 탐색 트리에서는 중복된 값을 허용하지 않기 때문에 다른 점이라고 할 수 있다.
힙의 종류
최대 힙
높은 키 값이 루트에 가까운 쪽에 위치하는 형태의 힙이다. 우선 순위 큐로 구현하여 dequeue를 할 시에 root 값 부터 나오게 되며 이러한 root 값은 힙 트리 내에서 가장 큰 값이다.
최소 힙
작은 키 값이 루트에 가까운 쪽에 위치하는 형태의 힙이다. 우선 순위 큐로 구현하여 dequeue를 할 시에 힙 트리 내에서 가장 작은 값이 나온다.
힙의 삽입과 삭제
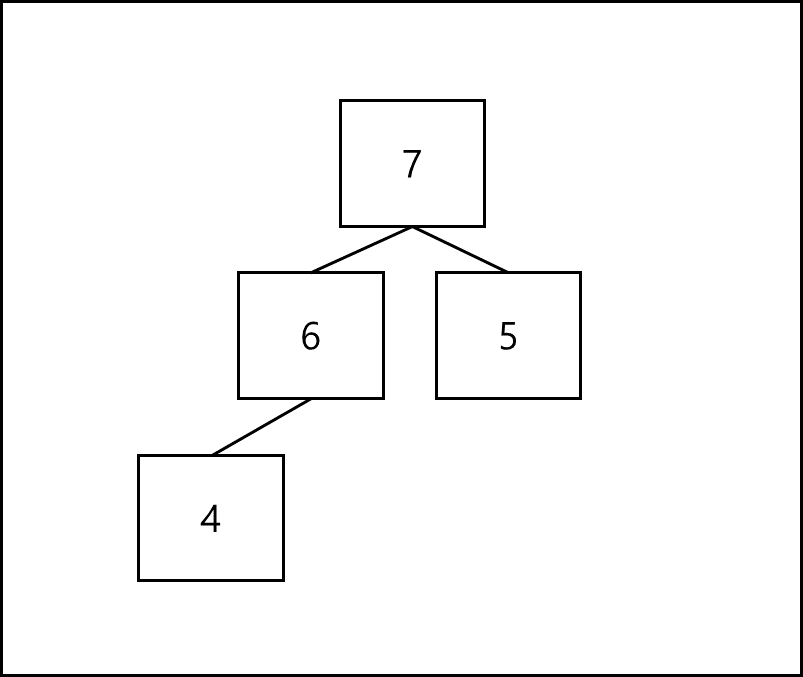
힙은 항상 root가 최소 혹은 최대 값인 규칙을 만족해야한다 따라서 삽입과 삭제시 해당 규칙을 만족하기 위해 일정한 연산이 필요하다. 최대 힙을 기준으로 서술해 보겠다. 일단 7,6,5,4가 삽입된 최대 힙이 있다고 가정해보겠다.
삽입
삽입은 인덱스 순으로 넣는다. 인덱스순이라는건 완전 이진트리 형태로 유지하기 위한 순서를 말하는데 왼쪽 자식 노드 부터 하나씩 채우는 형태인 것이다. 가령 8을 삽입한다고 해보겠다. 그러면 다음과 같은 형태가 된다.
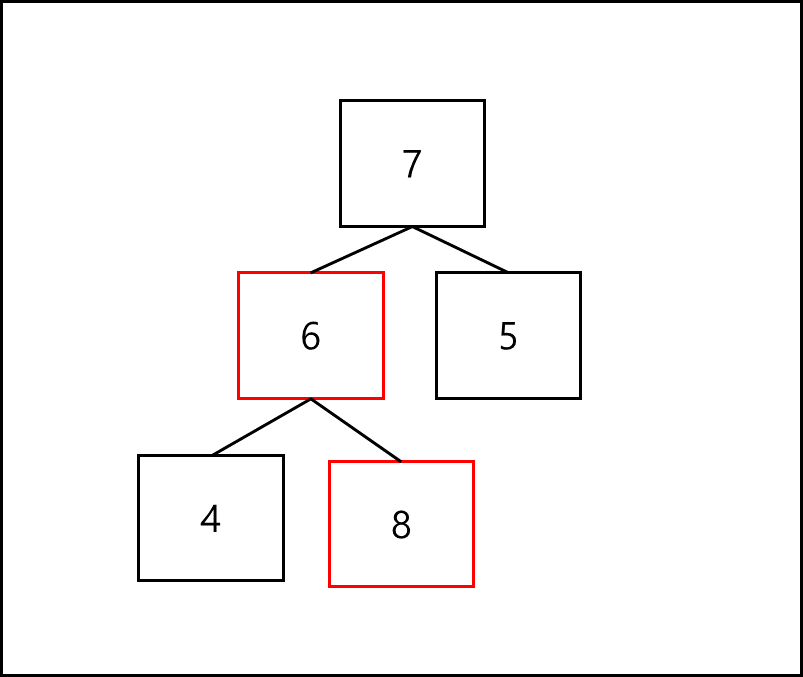이럴 경우 문제는 이거다. 부모 노드가 자식 노드보다 무조건 키 값이 커야한다. 그러면 8이 6의 부모 노드가 되어야한다. 따라서 6과 8을 교체한다. 
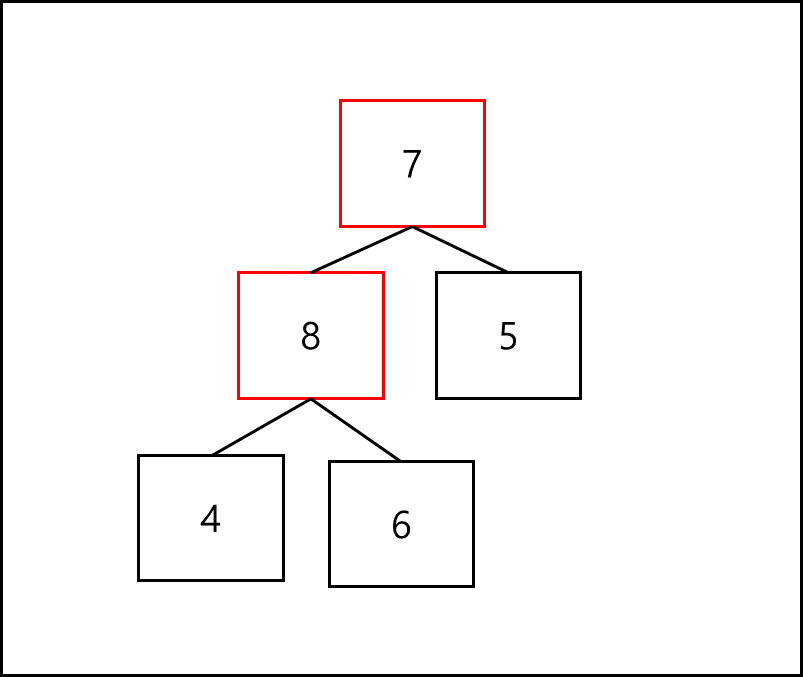그러면 루트 노드와 교체한 노드 간의 규칙 위반이 생기기 때문에 루트 노드 값과 방금 교체된 노드의 값을 교체한다.
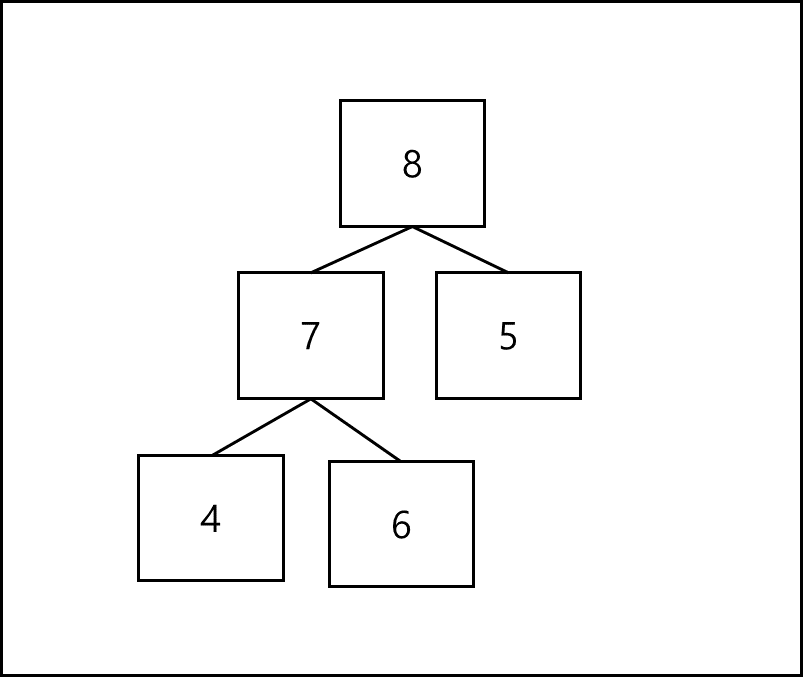그러면 최대 힙의 삽입이 완료된 것이다.
삭제
삭제는 루트 노드부터 제거한다.
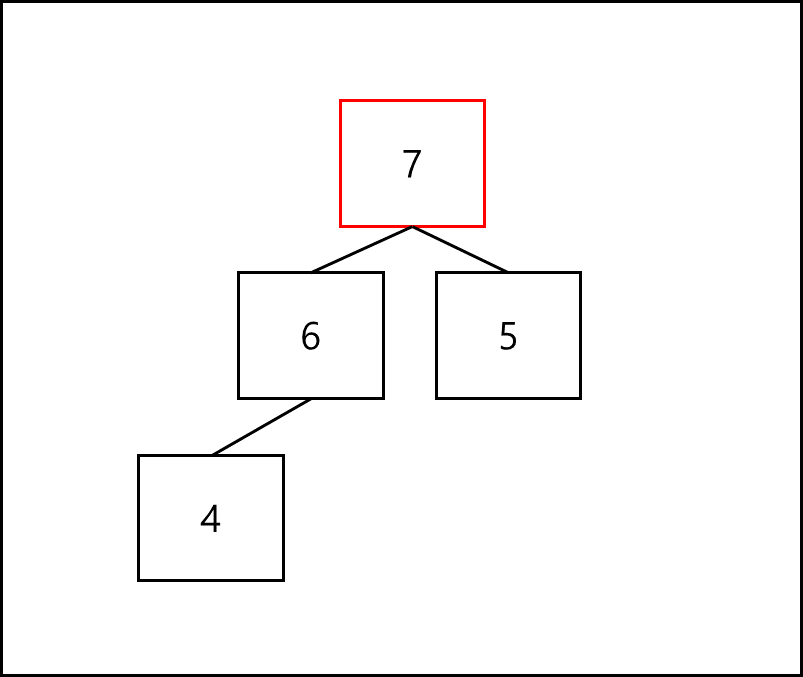제거된 루트 노드에 인덱스 상 가장 마지막 값을 올린다.
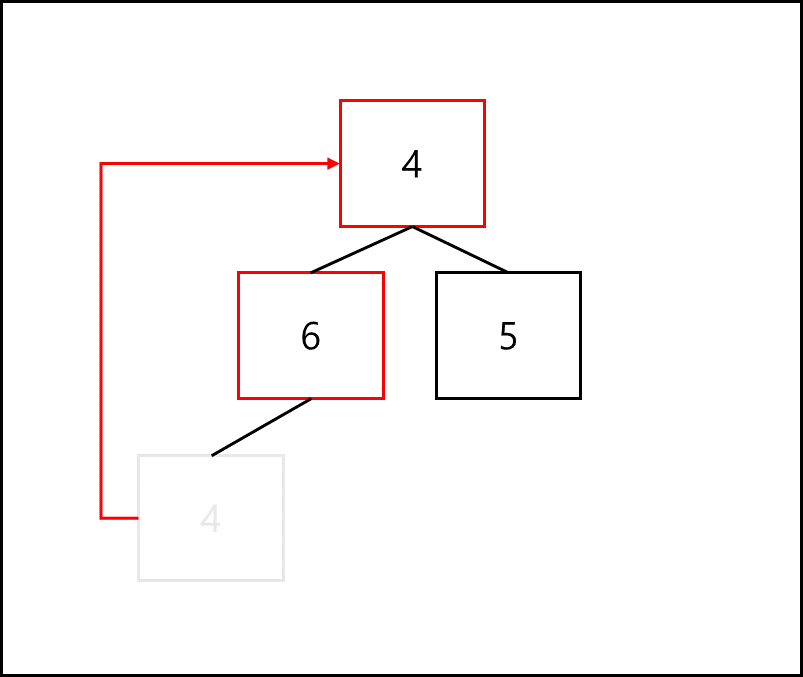이렇게 올리게되면 당연히 자식 노드 들과 규칙 위반이 생기는데 왼쪽 자식 부터 비교하여 자식 노드가 올라간 노드 값보다 크다면 교체를 해준다. 
최소 힙으로 삽입과 삭제를 구현하고 싶다면 최대 힙의 비교 부분을 반대로만 하면 최소 힙의 삽입과 삭제 연산으로 변한다.
힙의 구현
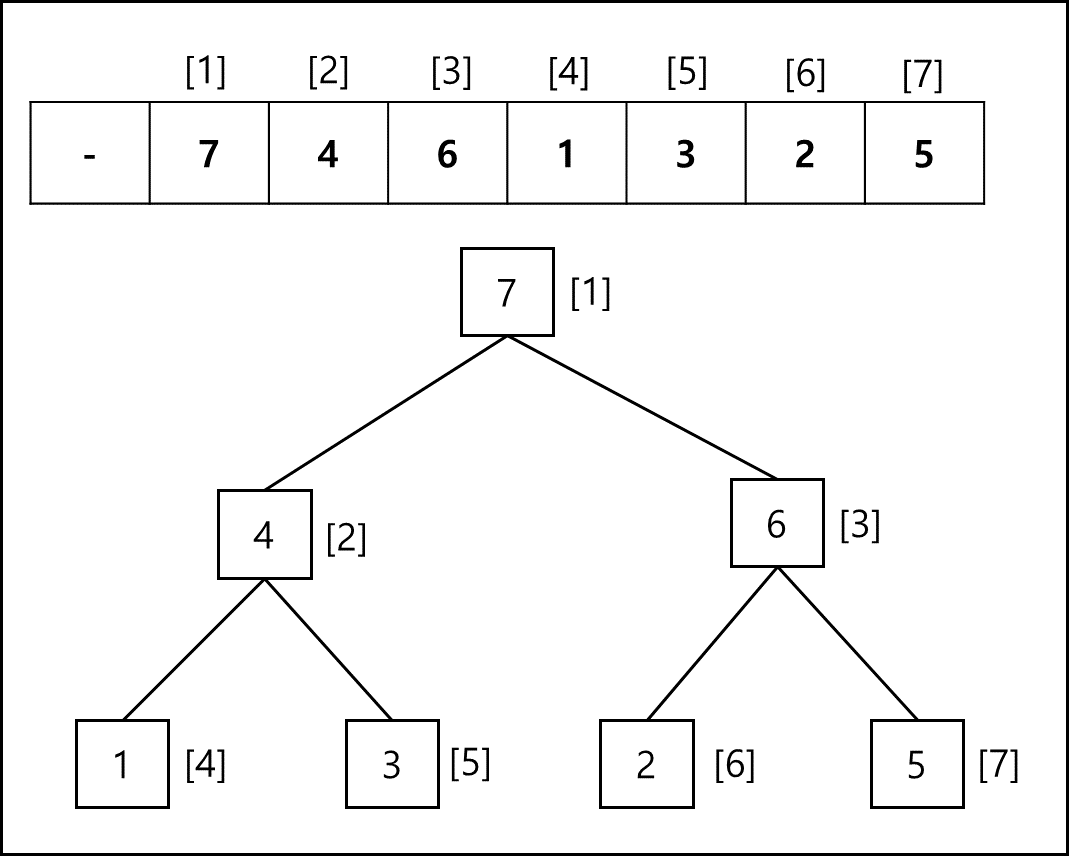
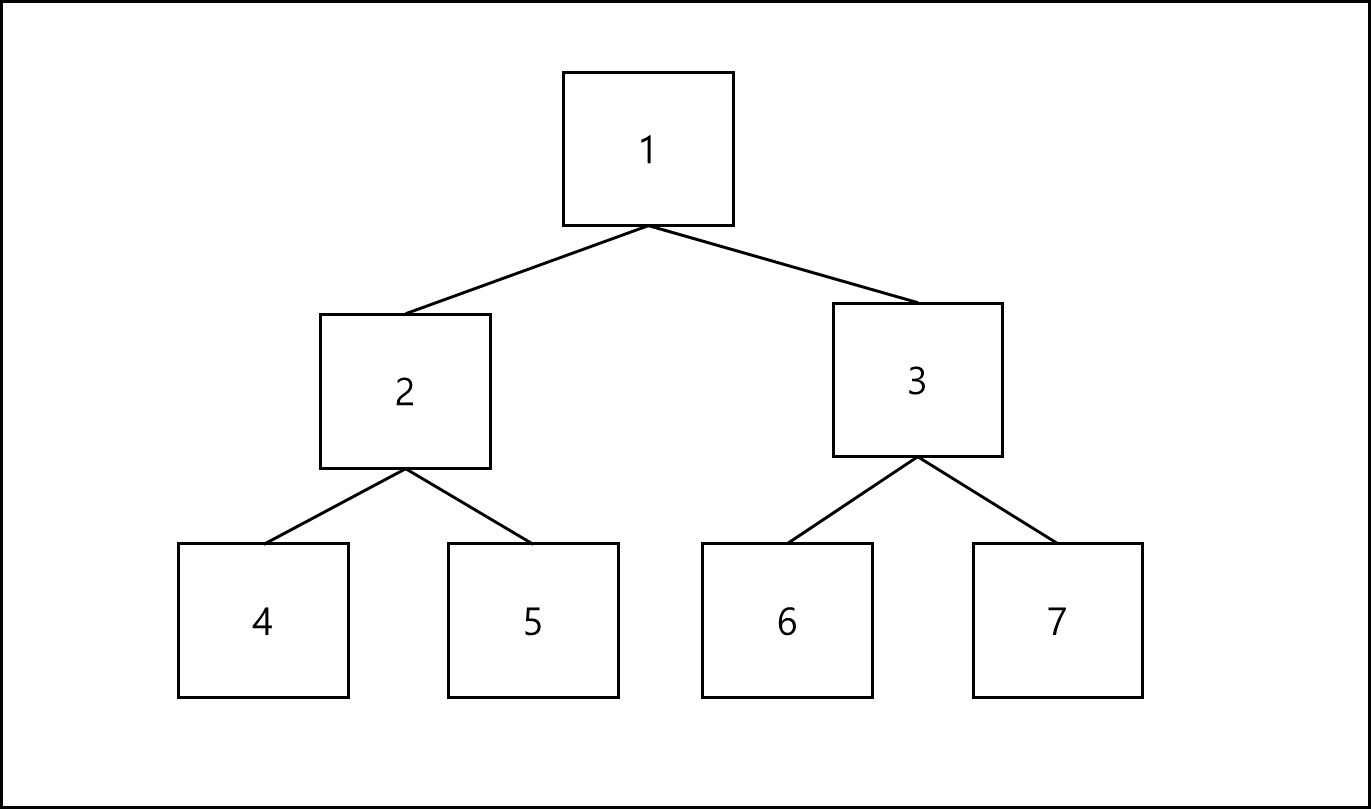
이러한 힙은 배열로 구현하면 굉장히 좋다. 트리 구조를 간단한 연산을 통해 배열의 index화를 통해 세팅이 가능하기 때문인데
배열의 0번지를 null로 비워둔다면 1번째를 root로 인덱스를 통해 쉬운 연산이 가능하다. 힙을 포화 이진트리 형태로 만들려면 총 2^n+2 (n은 정수)형태의 개수여야 한다.
- 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = 내림((자식의 인덱스) / 2)
