A * 알고리즘
A * 알고리즘
가장 대표적인 길찾기 알고리즘 중 하나이다. 기존에 있던 다익스트라 알고리즘 기반으로 개량된 알고리즘으로 스타크래프트가 이러한 A* 알고리즘을 이용하여 각 유닛의 길찾기를 구현했다고 알려져있기도하다.
이 알고리즘은 평가함수로 해당 경로를 갈지 말지를 평가하게 되는데 이 평가함수 f(N)은 다음과 같다.
\[f(N) = g(N)+h^{*}(N)\]- $g(N)$ : 초기노드에서 N노드 까지의 최단거리
- $h^{*}(N)$ : 원래 $h(N)$으로 N노드에서 목표노드까지 최단거리, 최적해를 구하지 않는 이상 알수 없으므로 추정치인 $h^{*}(N)$을 사용
이 $f(N)$ 값이 가장 작은 값을 가지는 노드를 선택하면 해를 빨리 구할 수 있다는게 이 알고리즘의 골자이다.
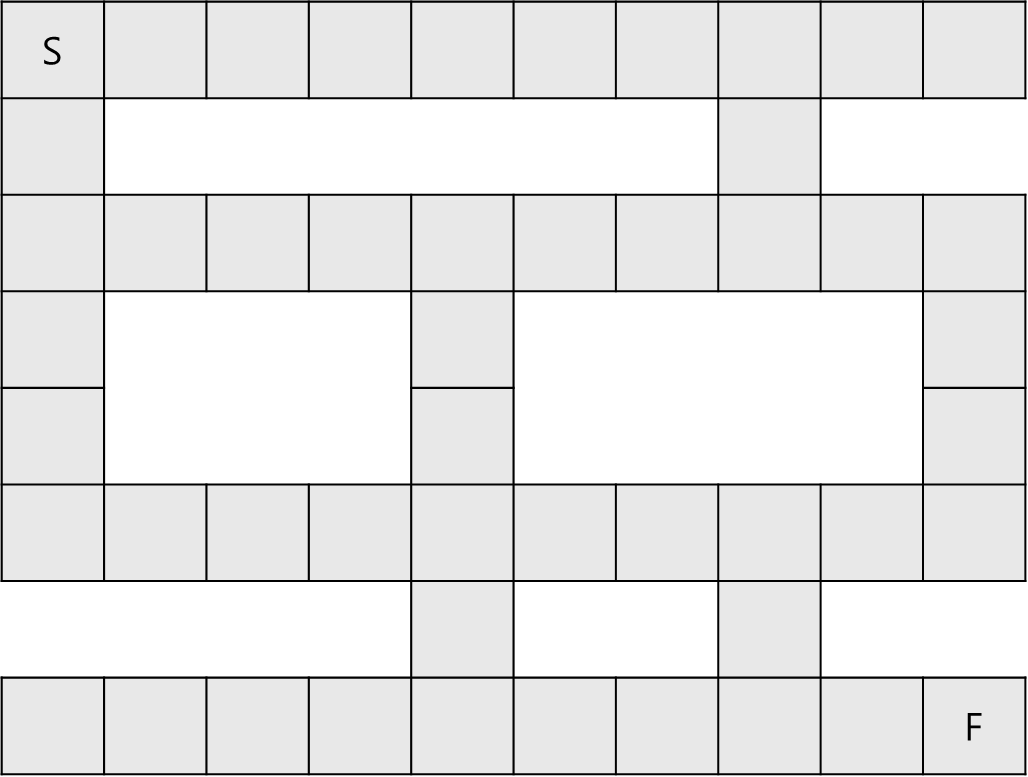
다음의 길거리가 있다고 해보자.
이 길거리는 가로 10칸 세로 8칸의 정사각형 셀들로 이루어진 길거리이다.
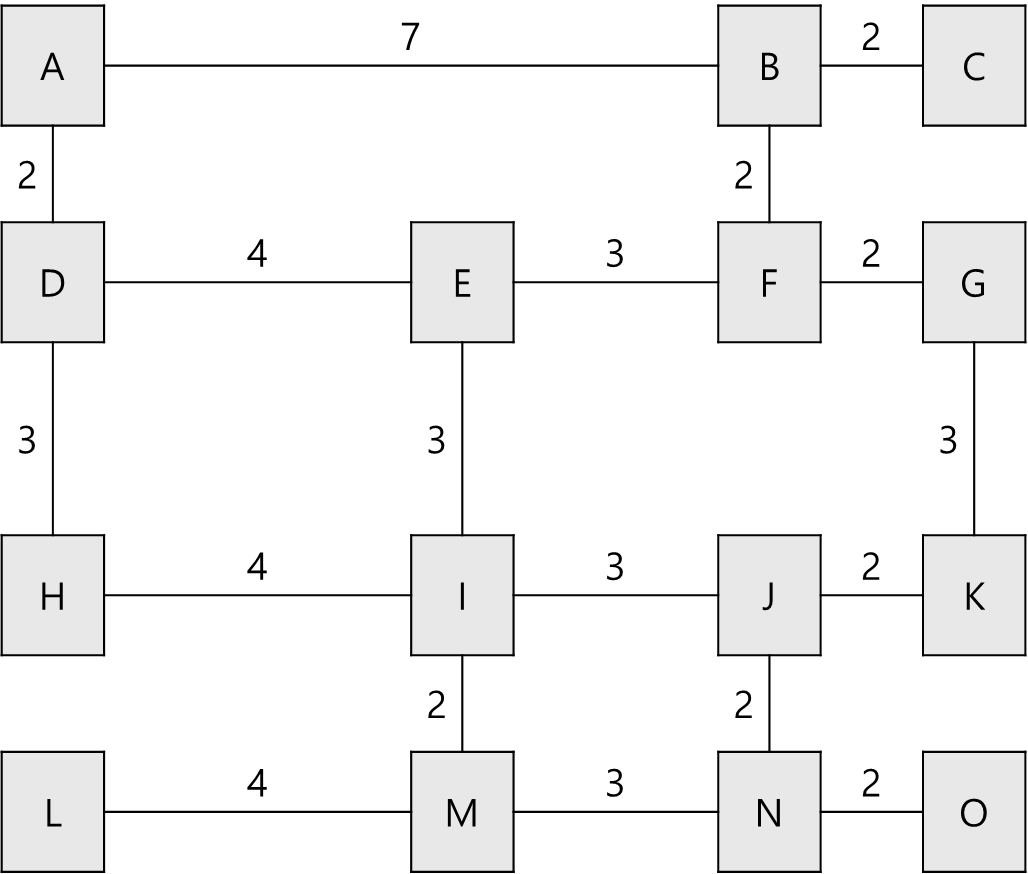
이 길거리는 다음과 같은 그래프로 단순화 시킬 수 있다.
다음 그래프에서 S에서 F로 간다고 할 때 최단 거리 알고리즘을 다익스트라로 구현하면 다음과 같이 시작점에서 가장 가중치가 작은 점을 기록하여 테이블로 유지하고 해당 가장 짧은 길을 따라 최단 거리를 찾게 된다.
그러나 다익스트라 방식에 치명적인 단점이 있었으니 그건 바로 실제로 가는데 필요하지도 않아보이는 노드까지 탐색하기 때문에 전반적으로 성능이 느리다는 점에 있다.
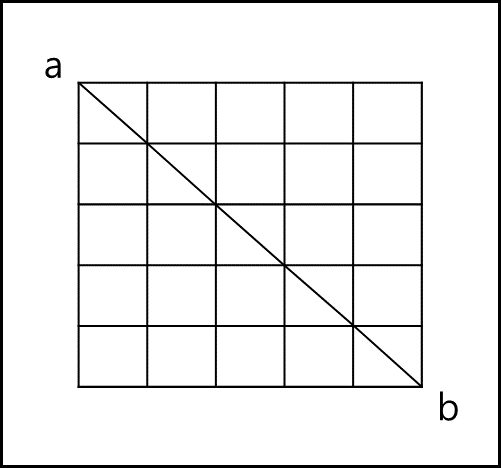
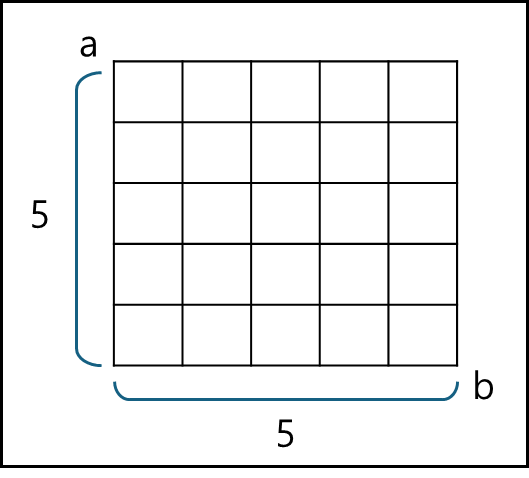
이러한 판단 오류를 수정하기 위해 휴리스틱 코스트라는 것이 추가되는데 $f(N) = g(N)+h^{*}(N)$ 식에서 $h^{*}(N)$ 값이 되겠다. 이러한 휴리스틱 코스트는 대상 노드에서 목적지까지의 거리를 값으로 사용하는데 두 가지 방법으로 많이들 사용한다.
이는 전혀 아닐 것 같은 경로를 제거하는데 아주 큰 도움이 된다.
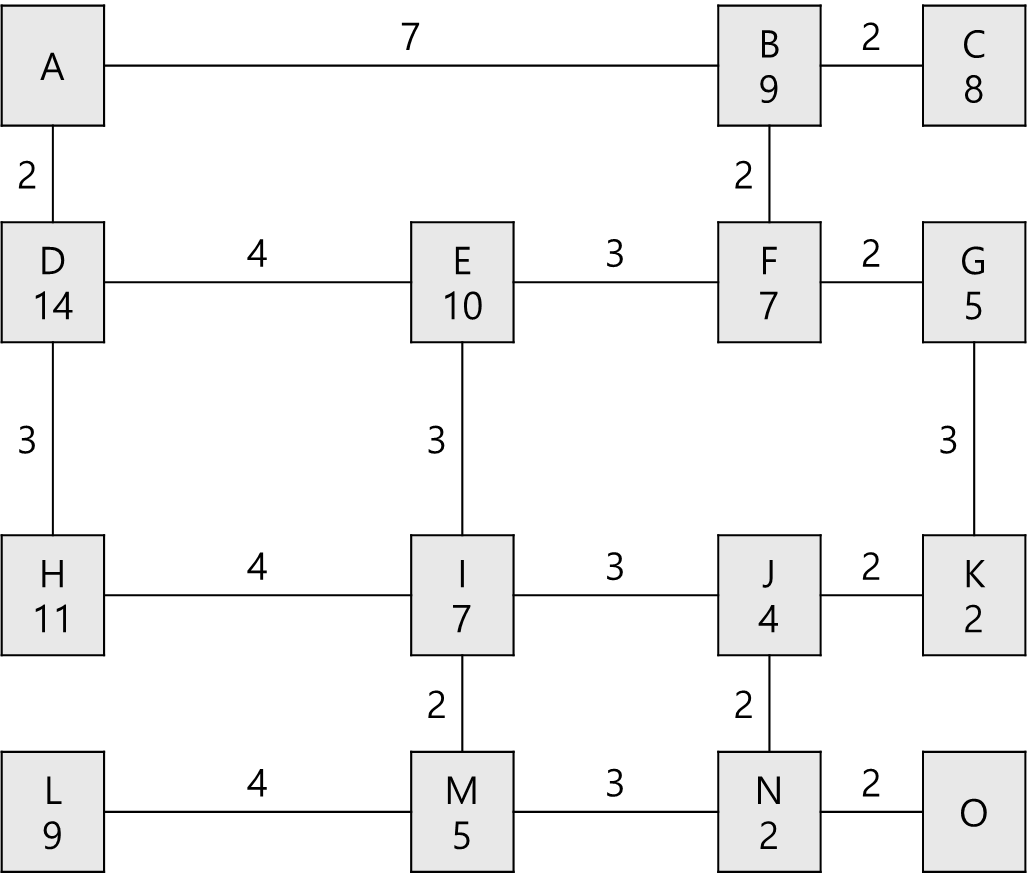
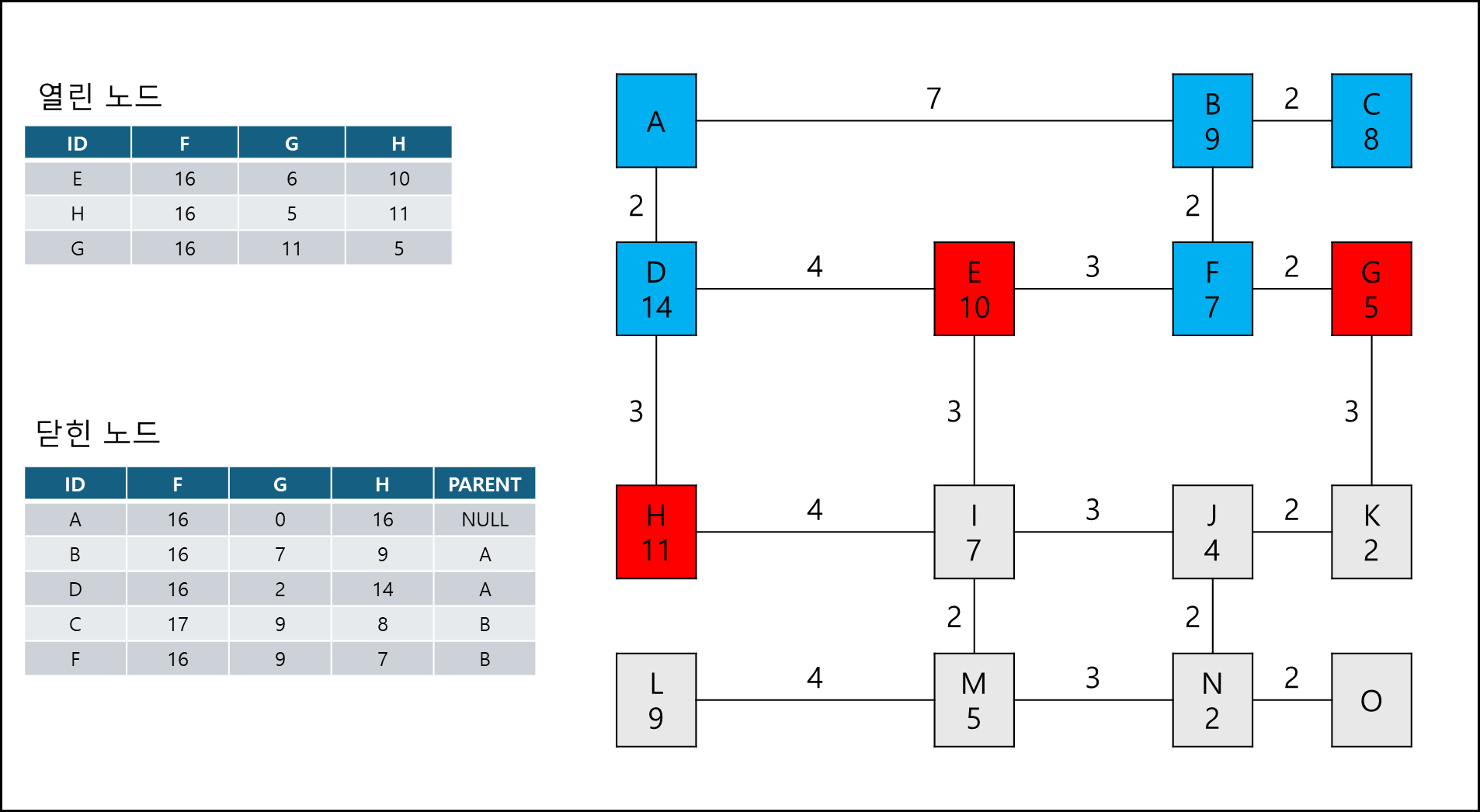
다음 아래의 그림을 보자. 각 노드에 맨해튼 거리로 가중치를 달아놨다.
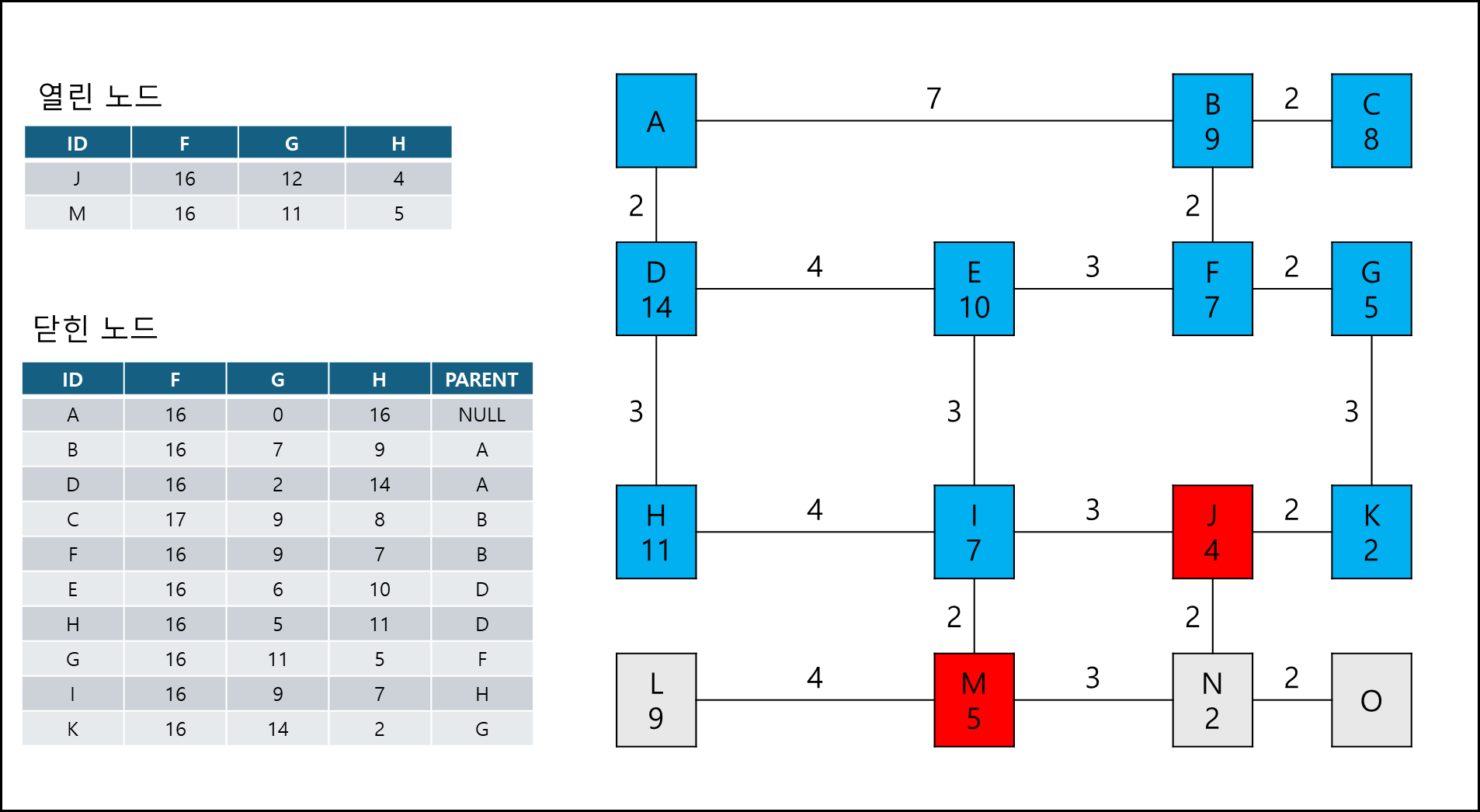
그리고 여기서부터는 다익스트라 알고리즘과 비슷한데 열린 노드와 닫힌 노드 개념이 필요하다.
닫힌 노드는 탐색을 마친 노드로 다음 탐색에 들어가지 않고, 열린 노드는 다음 탐색이 되는 대상으로 닫힌 노드와 연결된 노드들로 이루어져있다.
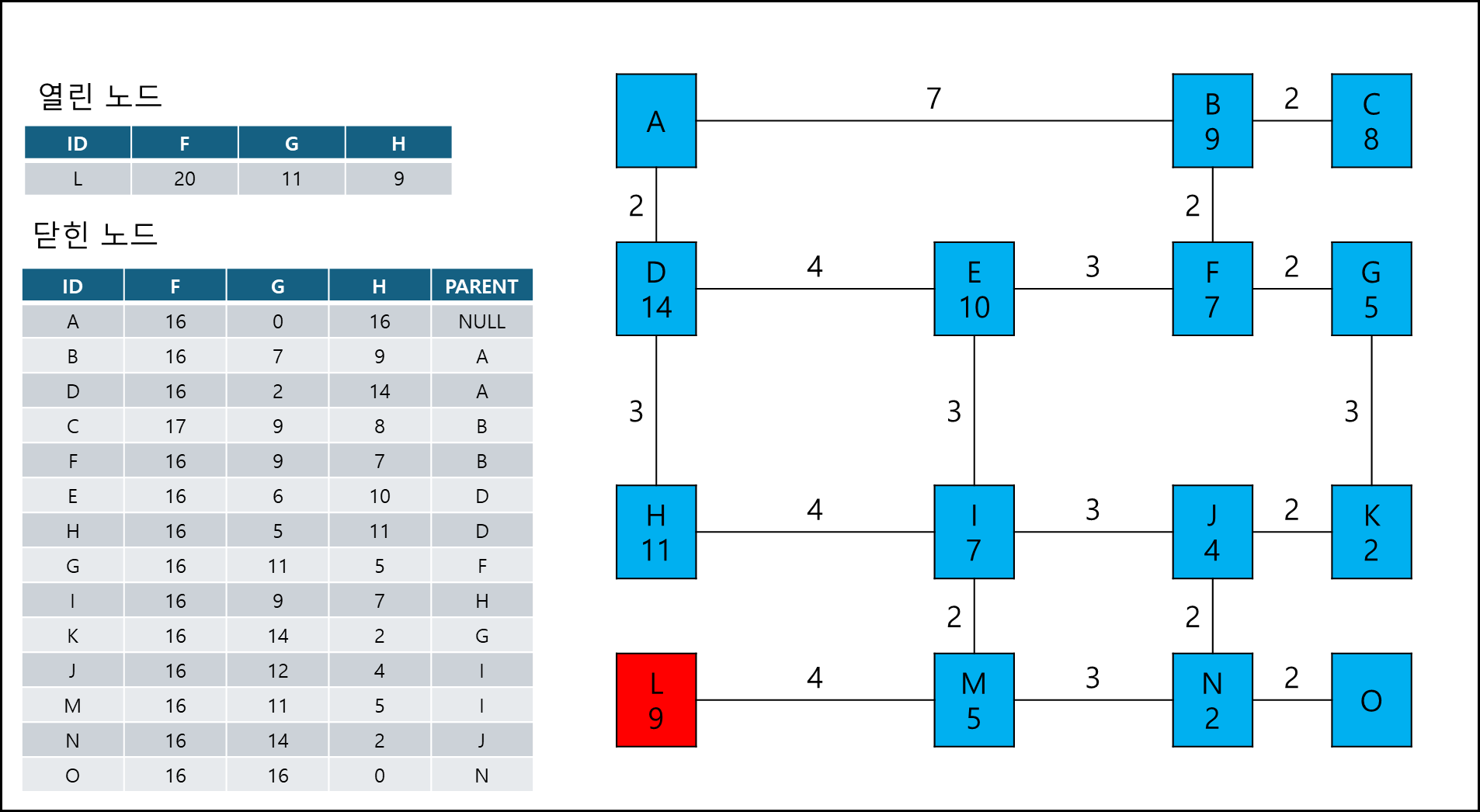
닫힌 노드는 지나온 값인 G와 목표까지의 거리 H, 그리고 부모 노드 ID를 갖고 있다. 따라서 막힐 경우 이전 부모로 돌아가 탐색을 계속하다가 최종 목적지에 도착하게 되면 해당 부모 ID 값만 출력하게 되면 경로가 완성된다.
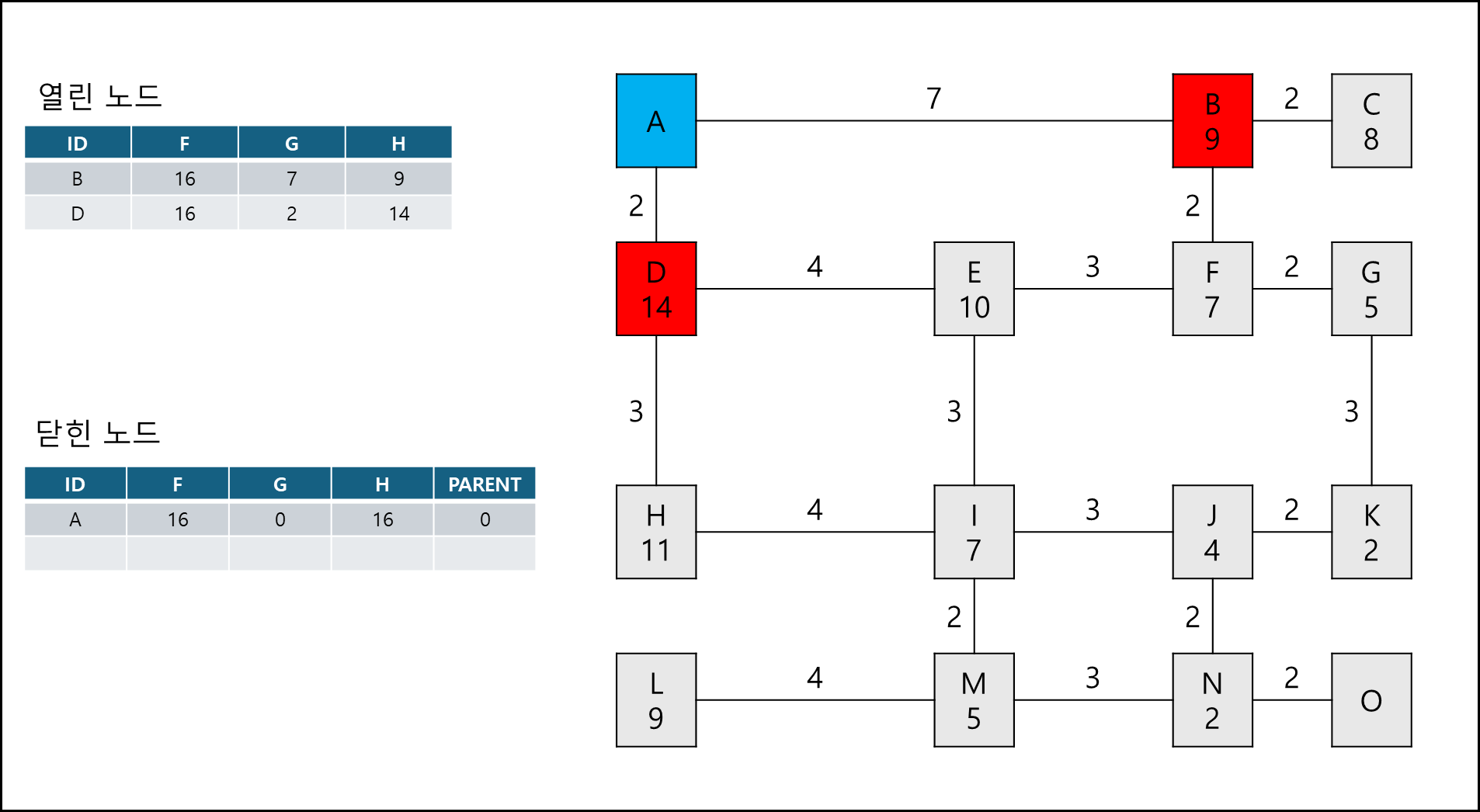
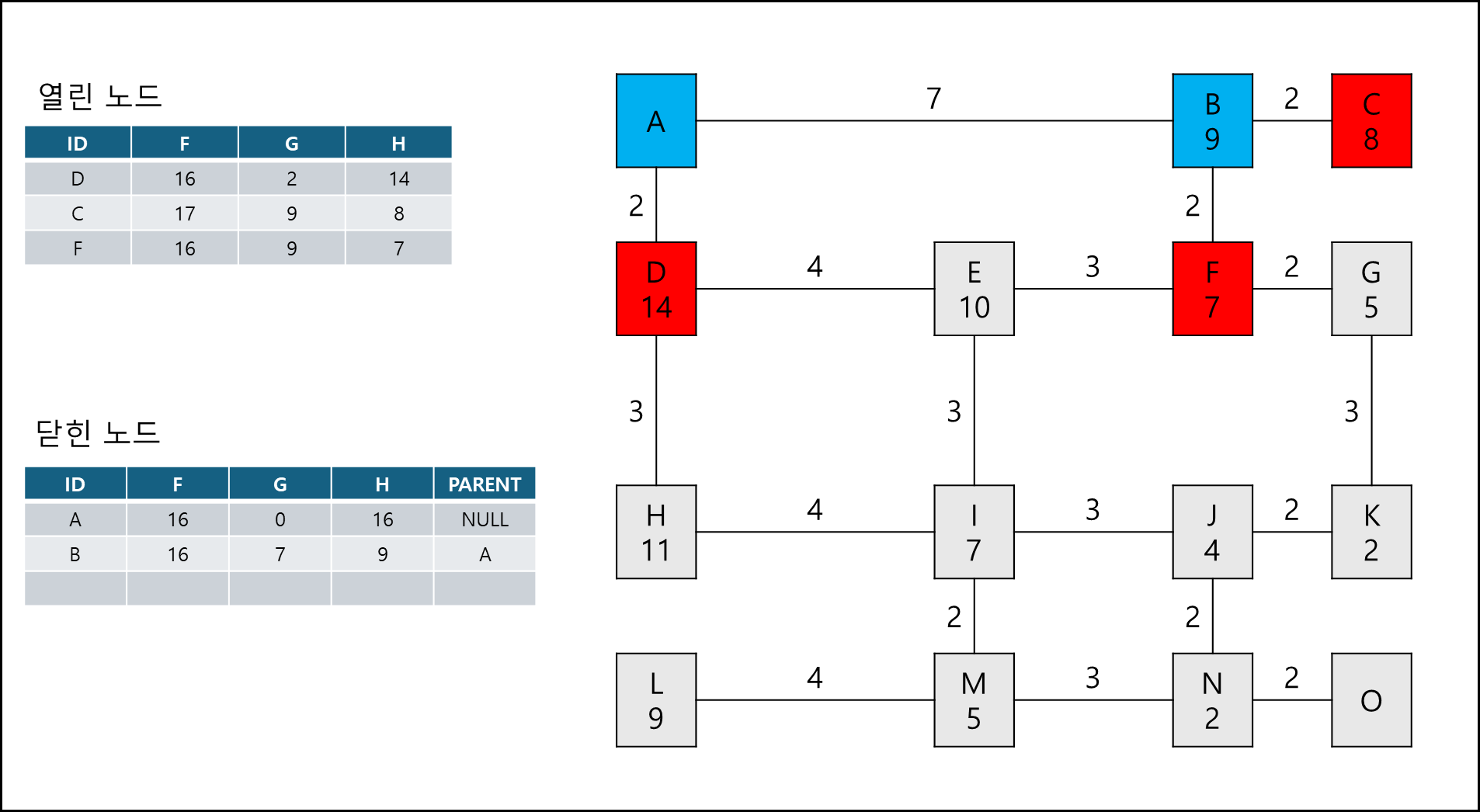
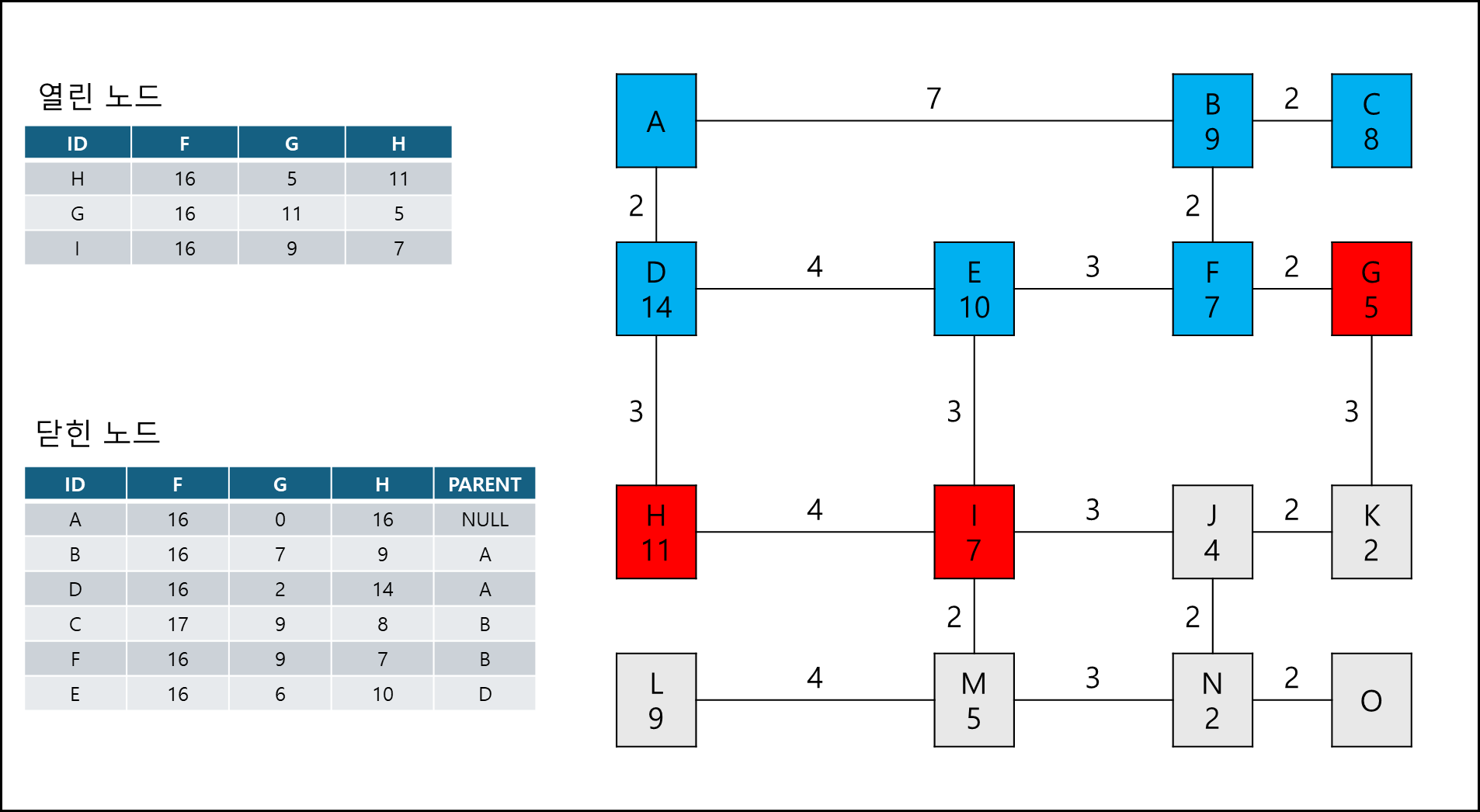
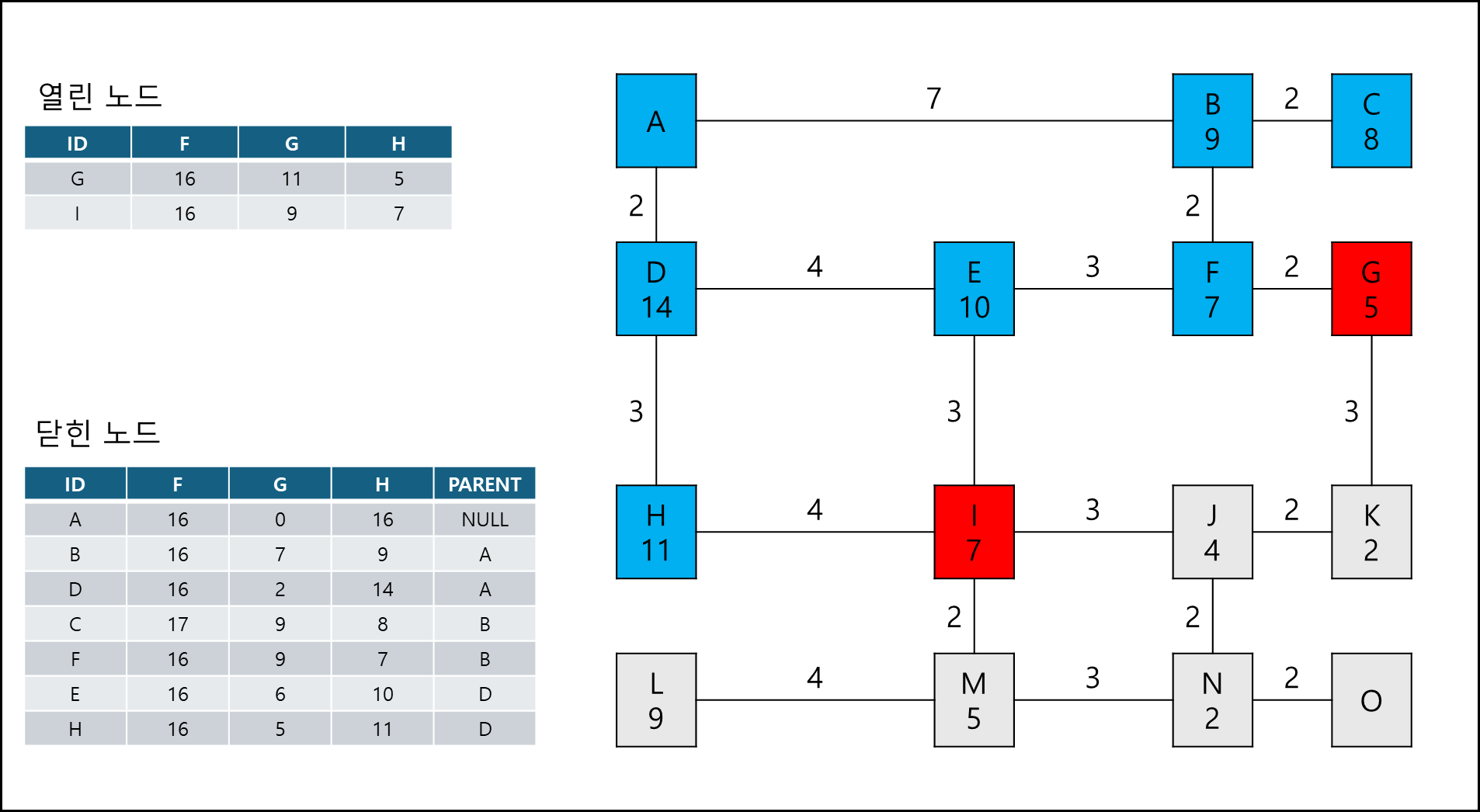
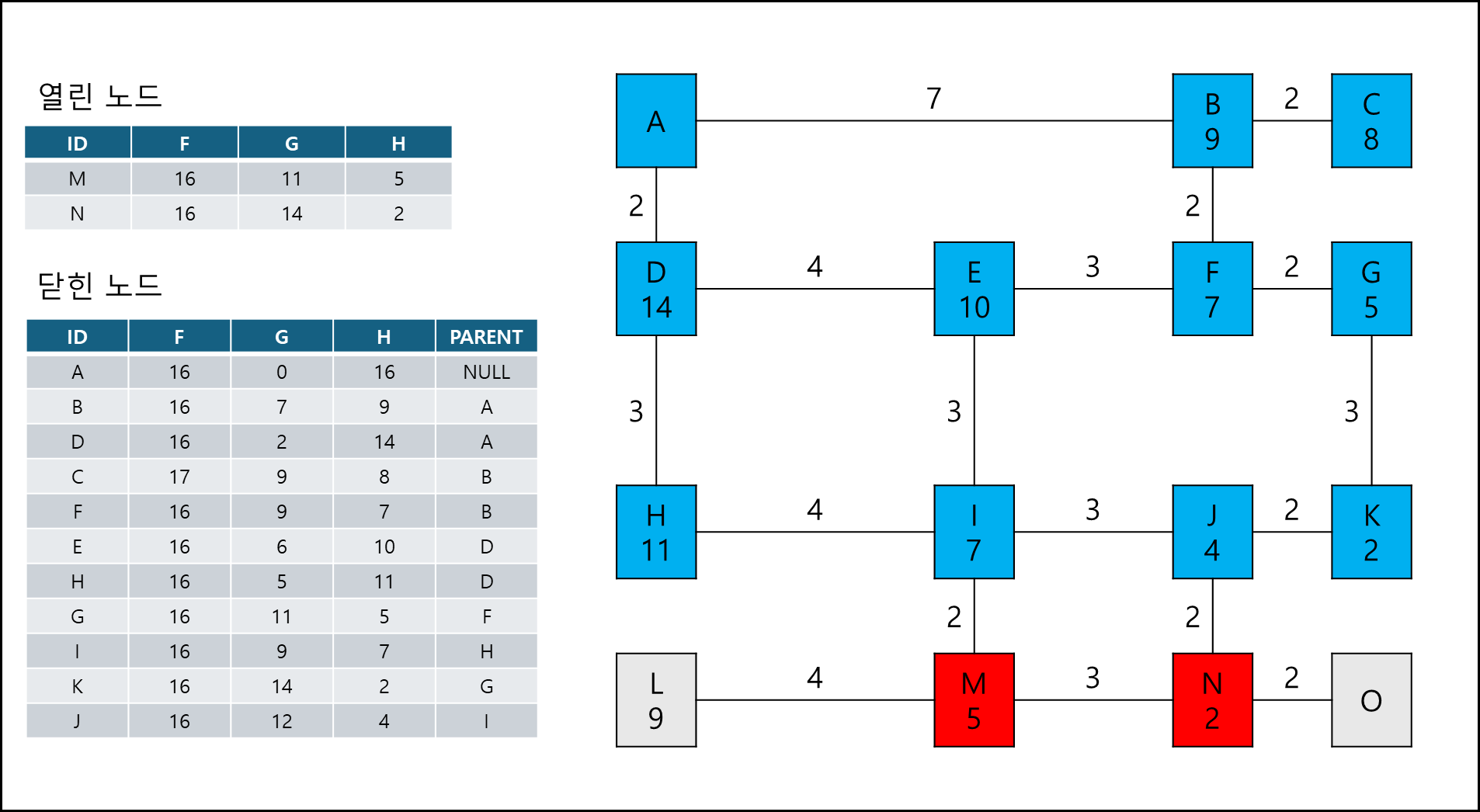
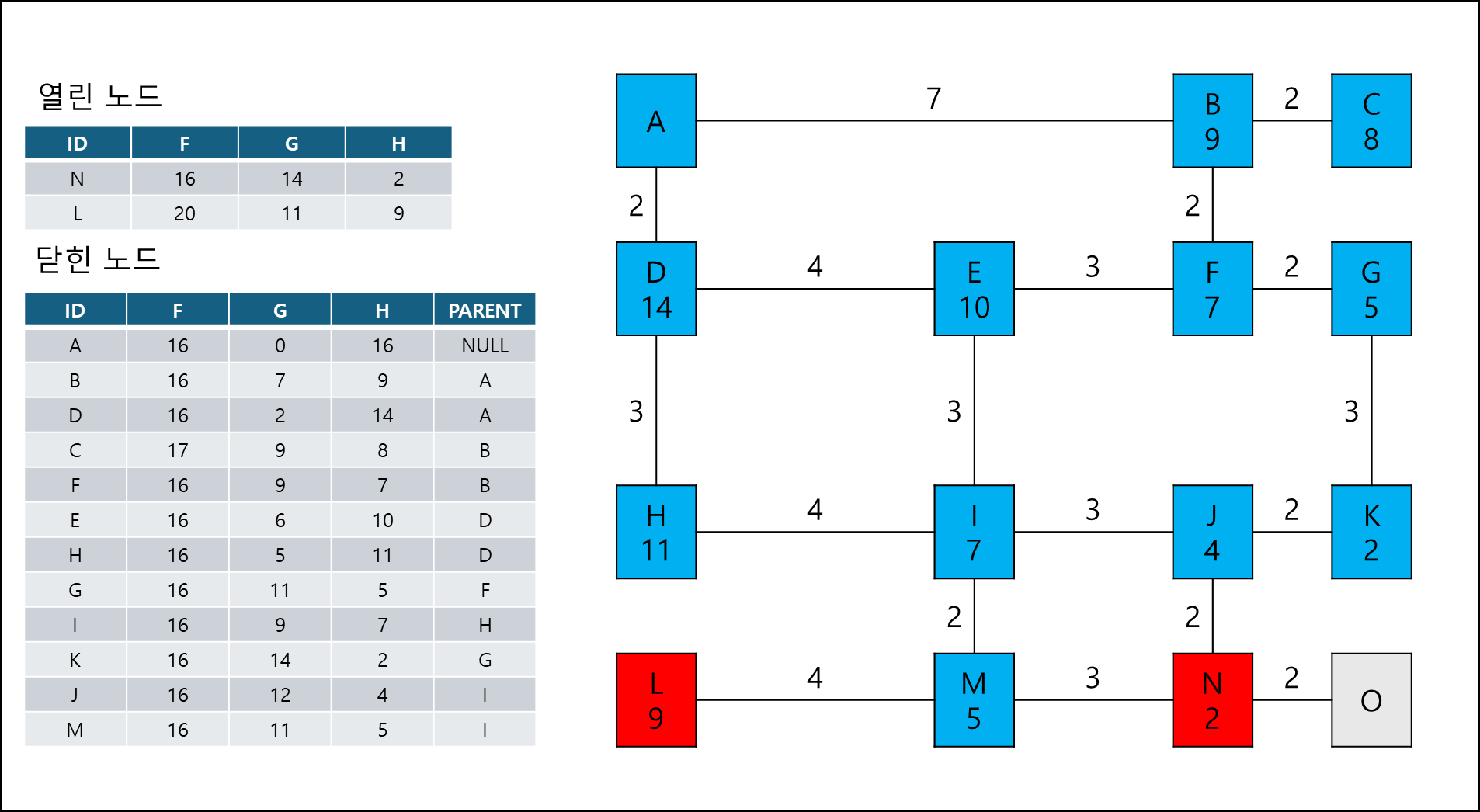
여기서 시작점 A에서 이동할때 노드 가중치 + 거리 가중치가 작은 쪽을 열린 노드에 추가한다.
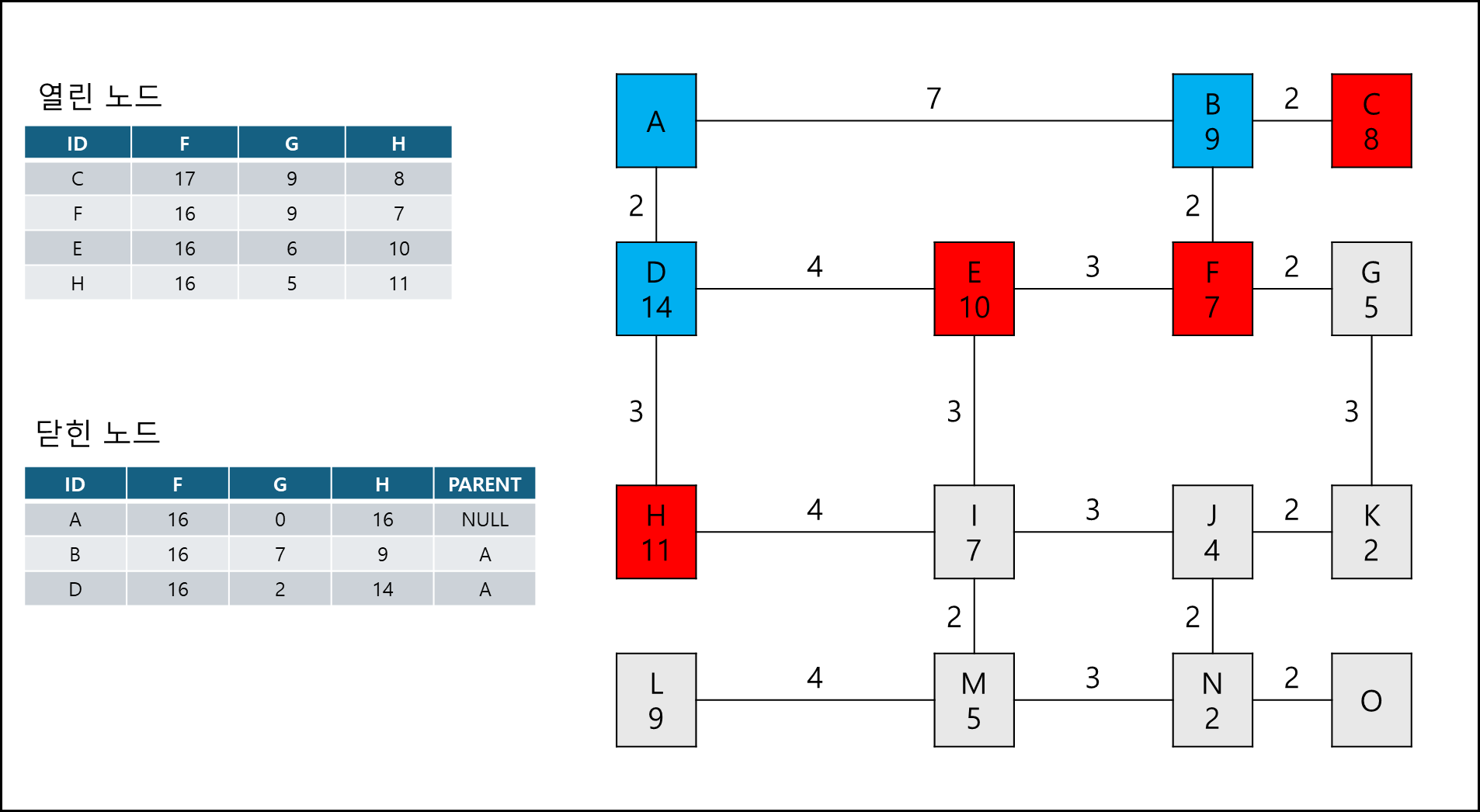
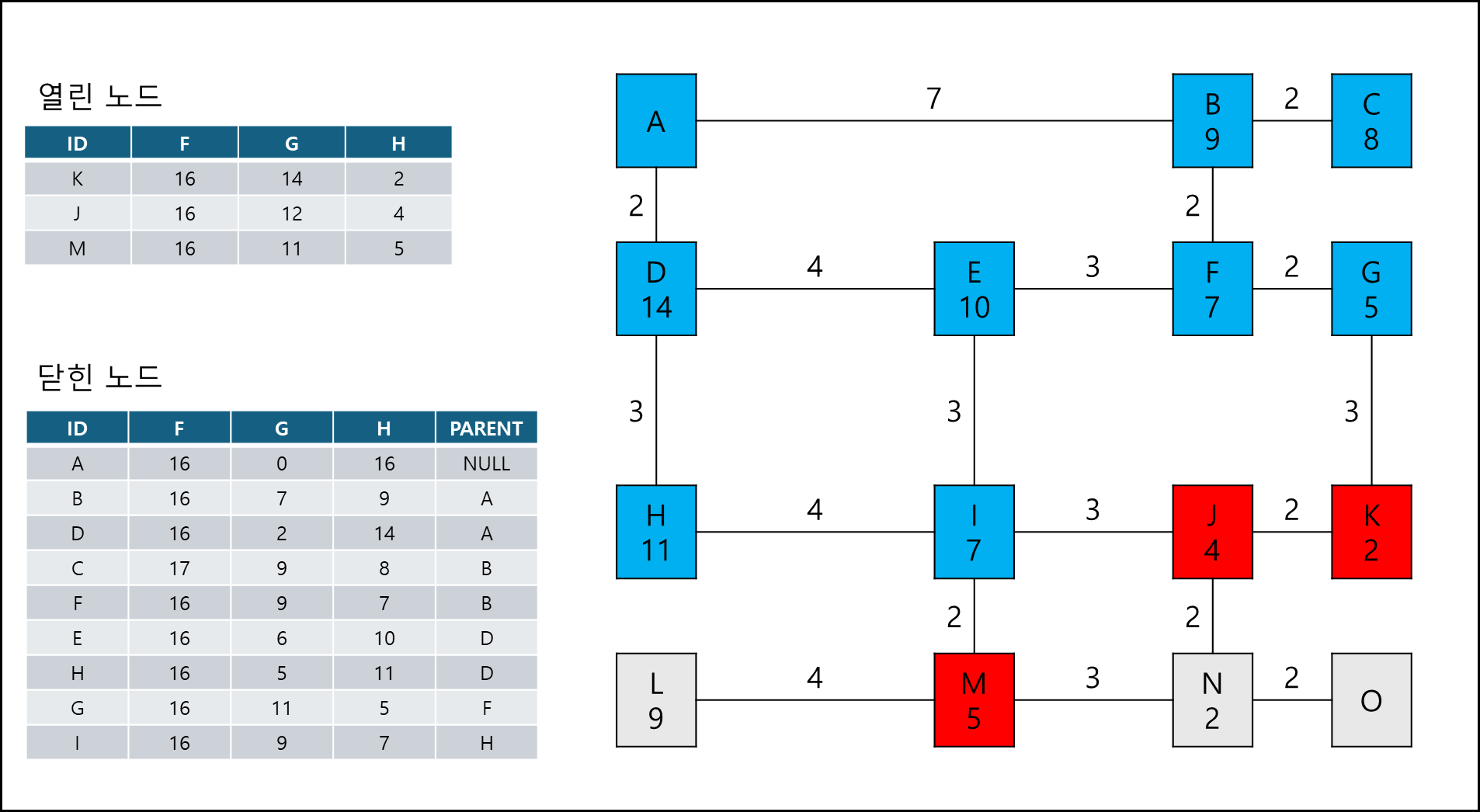
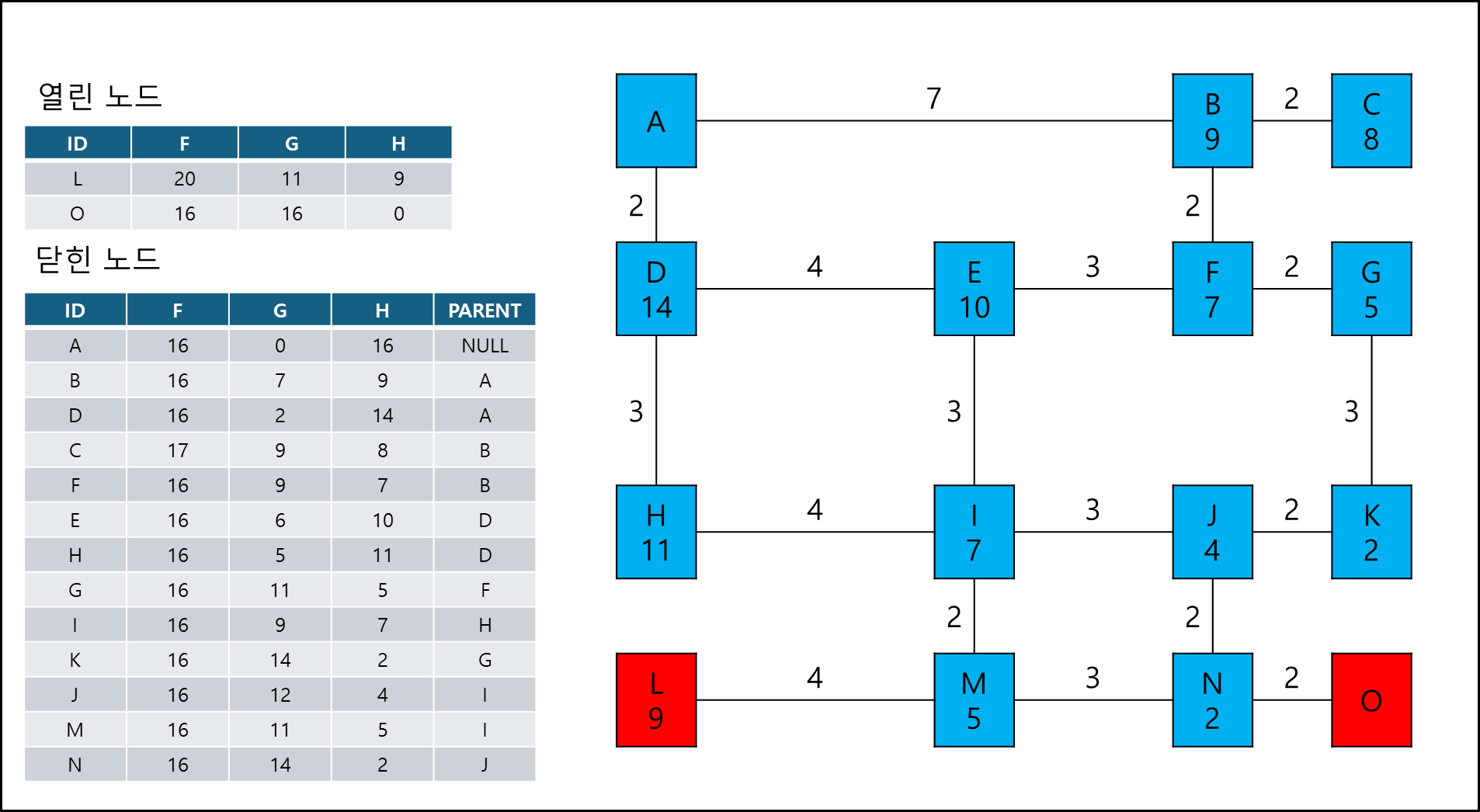
목적지 노드인 O 노드를 닫힌 노드 큐의 PARENT를 따라 역추적해보면 경로는 A-D-H-I-J-N-O 이다.
그리고 보니까 별로 더 효율적으로 보이진 않지만 (아무래도 예시를 잘못 만든듯하다)
아무튼 다익스트라보다 훨씬 효율적으로 최단 거리 경로를 찾을 수 있게 되었다.
참고 자료
- 인공지능 개념 및 응용 3판 Artificial Intelligence Concepts and Applications (2013년)
- GIS DEVELOPER - 최단 경로 탐색 – A* 알고리즘