Post

GPU 프로그래밍 - Marching Cube 알고리즘

Posted Updated
By Blake Woo 11 min read

Marching Cube 알고리즘

1. 개요

CT/MRI 스캔이나 부호 거리장 데이터와 같은 3차원 스칼라장에서 등위면의 다각형 메시(일반적으로 삼각형 메시)를 추출하는 데 사용되는 컴퓨터 그래픽 알고리즘이다.

2. 기본적인 아이디어

격자 무늬 판이 있다고 해보자.
어떤 모양을 Slice 하면 단면이 나온다.
이를 격자에 대치시키면 아래와 같다.

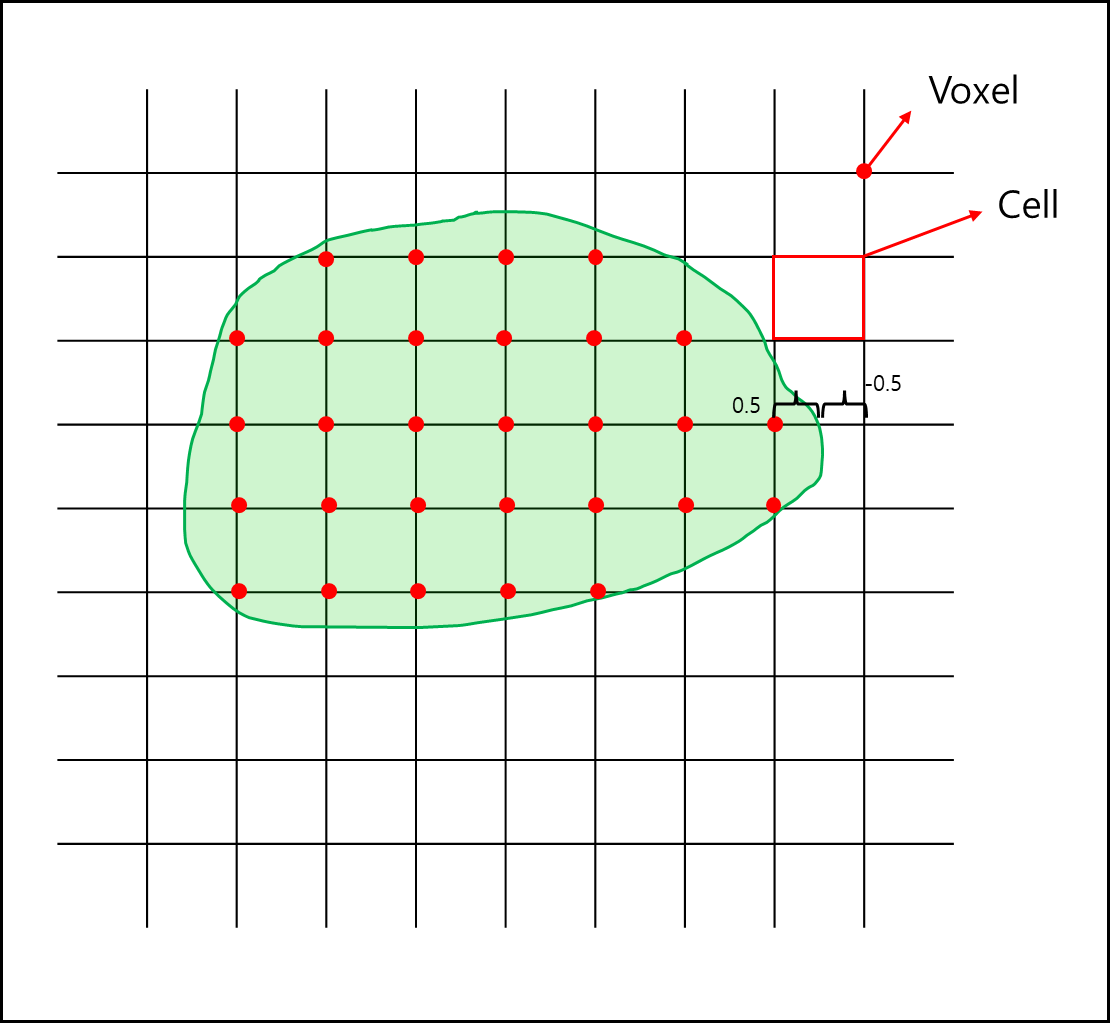
img.png

각 격자의 점을 voxel이라고 하고, 4개의 복셀로 감싸진 에지를 cell이라고 한다. (이는 2차원일때 그런 것이고 3차원의 경우 육면체가 cell이 된다) 단면 내에 포함된 voxel가 포함되지 않은 voxel로 나뉘게 되는데 이를 기준으로 해당 Voxel이 단면의 inside냐 outside냐를 1bit로 표현할 수 있으며, 단면의 외곽이 Voxel 사이의 어느정도를 지나느냐에 따라서 각각의 iso-value를 지정할 수 있다.
(물론 위와 같은 방식이 아닌 다른 방식도 많으나 일단은 이렇게 설명하겠다)

이 값들을 토대로 voxel 사이에 외곽이 어떻게 지나가는지 유추할 수 있으며 각 점을 연결하여 대략적인 외곽을 알아낼 수 있다.

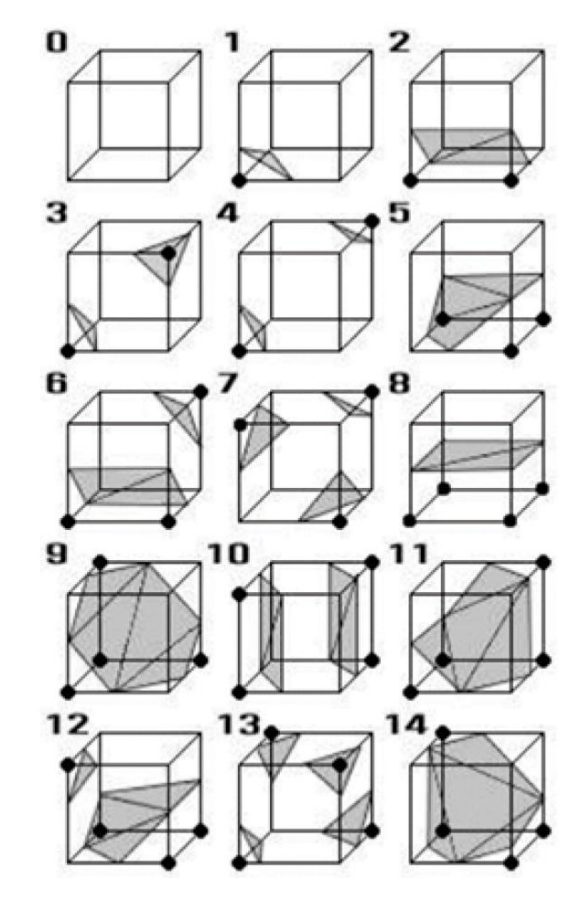
이를 3D로 확장시키면 8개의 Voxel에서 정육면체에 어떻게 외곽이 통과하는지 알아 볼 수 있는데 정육면체의 Voxel은 총 8개이고 각 상태가 1bit씩이니 $2^{8} = 256$ 개의 경우의 수가 나온다. 여기서 대칭이나 회전으로 동일하게 만들 수 있는 중복을 제외하고 나면 고유한 형태 15개만 남는다.

img_1.png

위 표현들을 잘 보면 알겠지만 모두 삼각형으로 표현 가능한 형태이다. 따라서 표현의 용이성과 데이터의 축소를 위해서 외곽선을 삼각형으로 연결해서 표현하는데 이를 폴리곤이라고 표현하며 일단은 한 개의 3D Cell에 대해서 표현하기 위해서는 아래와 같이 표현한다.

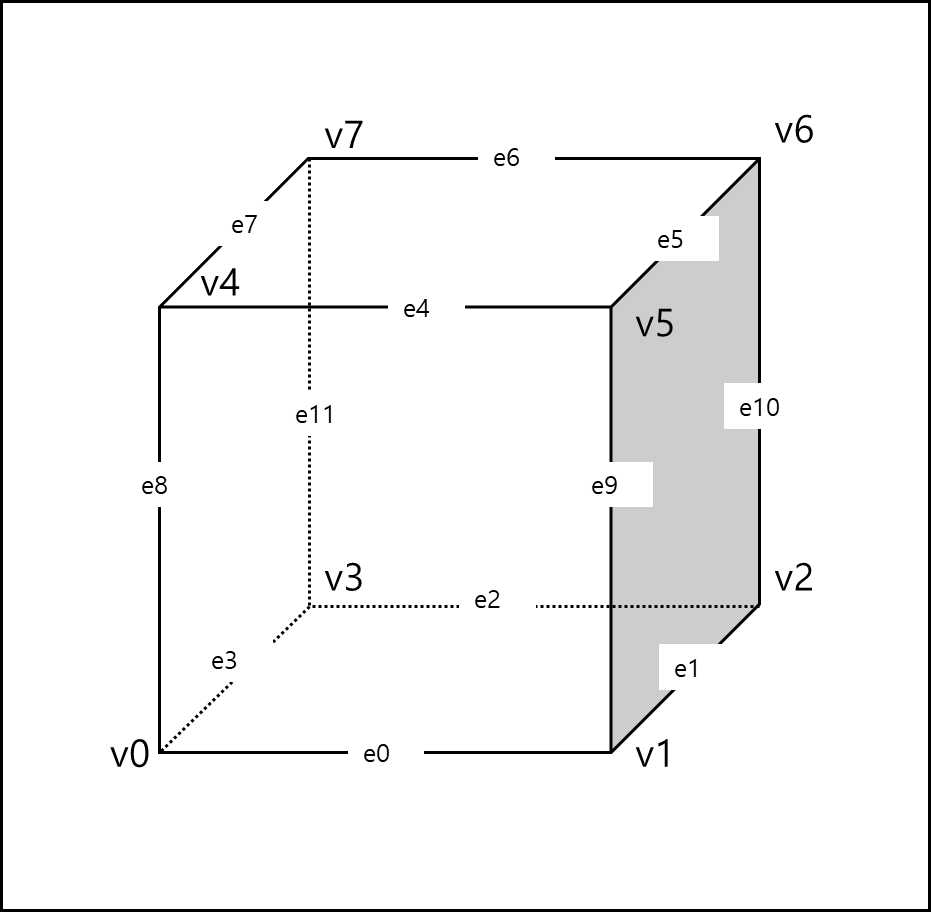
img_2.png

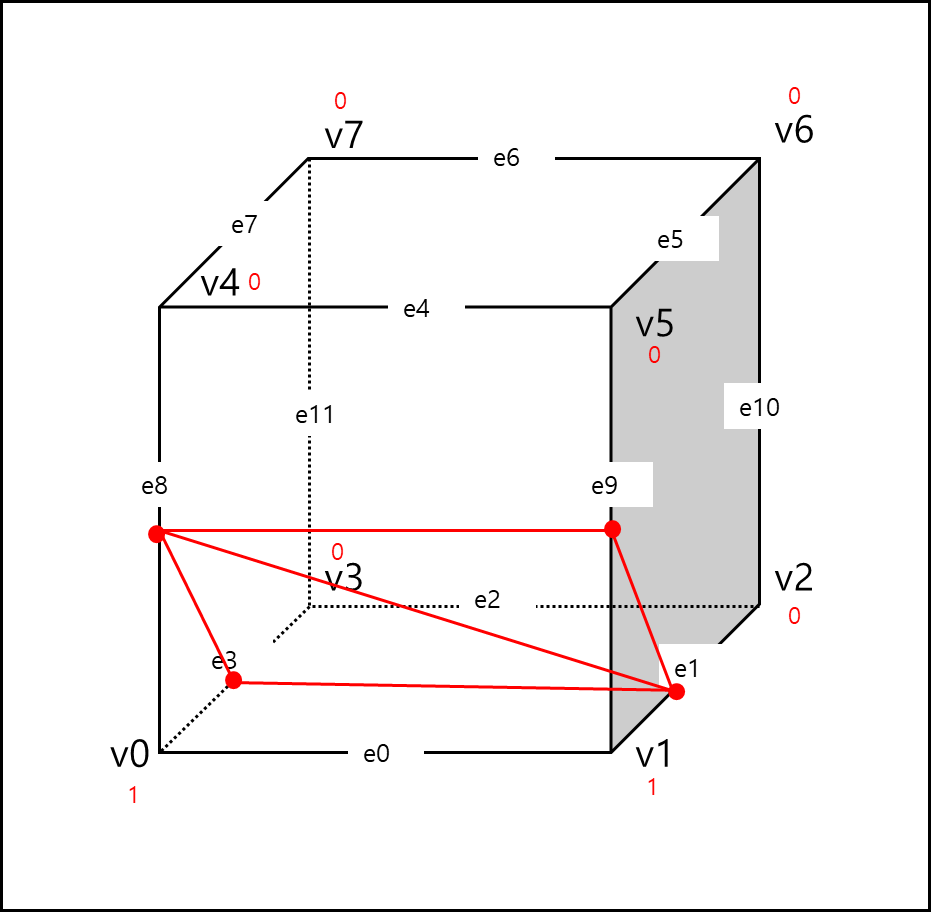
위와 같이 Cell을 정의하고 해당 셀을 지나는 외곽을 정의할때는 Cube Index, EdgeTable과 TriTable 그리고 NumVertsTable을 사용하는데 각 내용이 어떤 정보를 포함하는지는 예시를 통해 알아보겠다. 어떤 두 개의 삼각형을 정육면체 Cell에 표시한 예시이다.

img_3.png

v0, v1은 외곽선안에 있으니 1이고, 밖에 있는것은 0으로 표기했고 삼각형은 e1,e3,e8 과 e1,e9,e8을 이용하여 2개가 만들어져있다.
이를 위에 언급한 형태로 표현하면 아래와 같다.

cubeindex = v8,v7,v6,v5….v0 = 00000011 = 3;
EdgeTable = {e11,e10,e9 …. e0} = {0,0,1,1,0,0,0,0,1,0,1,0} = 0x30A;
TriTable = {1,8,3,9,8,1,255,…,255};
numVertsTable = 6;

  • cubeindex는 외곽선 안에 어떤 점이 있는지 Cell단위로 표시한 값이다. v0와 v1이 inside라 각각 1을 가지며 한 Cell당 8bit로 표현가능하기 때문에 3으로 표현 할 수 있다.

  • EdgeTable은 각 점이 어느 Edge를 지나는지 표현한다. 위 그림에서는 e9,e8,e3,e1을 지나기 때문에 위와 같이 표현하며 총 12bit로 표현가능하기 때문에 4bit씩 끊으면 16진수 3개로 표현 가능하다. 따라서 0x30A로 표현 가능하다.

  • TriTable은 각 점이 삼각형으로 연결되는 집합을 표현한 것이다. 1,8,3 한세트, 9,8,1 한세트로 총 2세트이며 그외에는 쓰지 않기 때문에 255로 채워져있다.

  • numVertsTable은 아까 중복 제거시 15개의 형태만 남는다고 했는데, 그 중에 몇번째에 해당하는지에 대한 내용이다.
    이전에 올린 그림과 대조해보면 6번 그림과 같음을 확인할 수 있다.

3. 전체 구현

1) Classify Voxel Kernel

여기서 아래의 두 개의 배열을 만든다.

  • d_VoxelVerts : 각 복셀이 생성할 정점의 개수를 저장하는 배열로 꼭지점이 8개이므로 256개의 경우의 수가 존재하며, 각 케이스마다 생성되는 생성되는 삼각형의 정점 개수가 미리 정해져잇는데, 이 배열에서 해당 정점 개수를 계산하여 배열에 저장한다.

  • d_VoxelOccupied : 각 복셀이 활성상태인지 아닌지 체크하는배열로, d_Voxel_Verts에서 해당 인덱스가 1 이상이라면 1, 0이라면 0으로 표기하여 해당 복셀을 그릴 것인지 안 그릴 것인지 배열이 갖고 있다.

2) Exclusive scan

누적합을 구하는 알고리즘으로 각 요소 이전까지의 모든 요소의 합을 구하는데, inclusive와는 달리 Exclusive scan은 배열의 제일 앞에 0을 하나 끼워넣은 배열에서 누적합을 구하며 원 배열의 가장 끝 자리 수와 Exclusive 누적합 배열의 가장 끝자리 수를 더하면 전체 값의 합이 된다. (이 배열을 d_voxelOccupied_scan이라고 하겠다)

이 과정에서는 d_VoxelOccupied을 대상으로 Exclusive scan을 수행하게 된다.

3) Get active Voxels(# of active voxels) in host

위에서 언급했듯이 원 배열의 가장 끝 자리 수와 Exclusive 누적합 배열의 가장 끝자리 수를 더하면 전체 값의 합이 되는데 d_Voxel_Occupied 값을 기준으로 말하자면 전체 활성화 복셀의 수를 구할 수 있으며 d_VoxelOccupied 끝자리와 d_voxelOccupied_scan의 끝자리 수를 더하면 전체 활성화 복셀의 수이다.

4) Compact Voxels Kernel

Voxel 개수를 압축하는 것이다. 여기서 말하는 압축이란 d_voxelOccupied 배열에서 1인 값들의 인덱스를 갖고 있는 배열을 만드는 것이다.
차후 복셀의 활성화 여부를 구할때 d_voxelOccupied를 확인할 필요없이 압축된 배열(여기서는 d_compVoxelArray라고 하겠다)만 처음부터 확인하면 대상 활성화 복셀을 알 수 있다.

5) Exclusive scan form d_voxelVerts

d_VoxelOccupied가 아닌 d_VoxelVerts에 대해서 exclusive scan을 수행하여 d_voxelVertsScan 배열을 만든다.
첫복셀부터 끝 복셀까지 생성해야될 모든 정점들의 총 개수를 뜻하며, 각 복셀이 생성할 삼각형의 정점들을 최종 결과 배열의 어느 위치에 저장해야하는지 시작주소를 알려주는 역할을 한다.

6) Get totalVerts(# of generatd vertices) in host

총 생성해야할 정점의 수를 이전에 생성한 d_voxelVertsScan의 마지막 값과 d_VoxelVerts의 마지막 값을 더하여 구한다.
최종 결과 배열의 메모리를 할당하기 위해 필요한 값이다.

7) Get the pointers d_pos and d_normal to the OpenGL’s VBO

VBO(Vertex Buffer Object)는 정점 데이터를 GPU 메모리에 저장하는 OpenGL의 객체로, 복잡한 연산은 GPU에서 하지만 이를 그리는 것은 OpenGL을 통해 그리기 때문에 필요한 것이다. 여기서 말하는 d_pos는 정점의 위치, d_normal은 법선 벡터데이터를 저장할 VBO를 가리키는 포인터를 말한다.

8) Generate Triangles kernel

실제로 삼각형을 생성하는 CUDA kernel을 실행시키는 단계로, 활성 복셀(d_compVoxelArray)의 대상만을 가지고 병렬로 실행된다.
각 스레드는 담당한 활성 복셀에 대해서 Marching Cube 알고리즘을 수행하여 삼각형과 법선 벡터를 계산하며 계산된 정점 데이터는 d_voxelVertsScan을 참조하여 d_pos과 d_normal가 가르키는 메모리 공간에 바로 저장된다.

9) Return the control for the VBO’S to OpenGL

연산이 끝났으니 VBO에 대한 제어권을 OpenGL에게 다시 돌려준다.

※ 추가 업데이트 및 검증 예정

참고문헌

  • 서강대학교 임인성 교수님 - 기초 GPU 프로그래밍 수업 자료
  • Lorensen, W.E. and Cline, H.E. (1987). Marching cubes: A high resolution 3D surface construction algorithm. ACM Computer Graphics, 21(4). (SIGGRAPH ‘87)
  • Claudio Montani , Riccardo Scateni and Roberto Scopigno . A modified look-up table for implicit disambiguation of Marching Cubes. The Visual Computer, 10(6), pp. 353-355.
  • NVIDIA - NVIDIA ADA GPU ARCHITECTURE
  • NVIDIA - ampere architecture White paper
GPU Programming
GPU Marching Cube
This post is licensed under CC BY 4.0 by the author.