Mini Max 알고리즘
Mini Max 알고리즘
개요
상대방과 번갈아가면서 수를 두는 형태로 겨루는 게임의 AI를 짜는데 자주 사용되는 알고리즘이다.
최선의 수를 두었을 때의 이득을 계산하는 것이 아닌 실패했을 때 손실을 최소로하는 방향으로 탐색하는 방식이다. 영어로는 Minimax algorithm, 한국어로는 최소최대 알고리즘이라고 한다.
해당 알고리즘을 사용할 수 있는 게임의 룰은 아래와 같다.
- 둘이 하는 게임이어야한다.
- 차례대로 수를 두는 게임이어야한다.
- 제로섬 게임 : 둘 중 한 명은 패배하는 게임이어야 한다.
매턴 참가자가 수를 두는 경우 그 참가자의 둔 수에 따라 상대방의 둘 수 있는 경우의 수가 달라진다. 이 양상을 자료구조화 하면 트리로 나타낼 수 있는데 각 참가자가 턴을 진행하며 수를 두게 되면 두는 수에 따라 트리의 깊이는 1씩 깊어진다.
각기 참가자는 그 시점에서 가장 최적의 수를 선택한다. 일반적인 사람이라면 최적의 수에 대해서 직관적으로 혹은 경험적으로 알고 있겠지만 이걸 컴퓨터가 구동할 수 있게 하려면 추상화가 필요하다.
따라서 각 참가자가 둔 수를 정의한 노드에 점수를 붙인다. 이 점수는 평가함수를 사용하여 해당 노드의 상황을 정의한 것으로 현재 유리한지 불리한지를 나타내는 척도이다.
누구에게 불리한지 혹은 유리한지 나타내기 위해서 게임에 참가하는 둘을 각각 minimizer와 maximizer로 정한다. 평가함수값이 크면 maximizer가 유리하고, 작을 수록 minimizer에게 유리한 것이다.
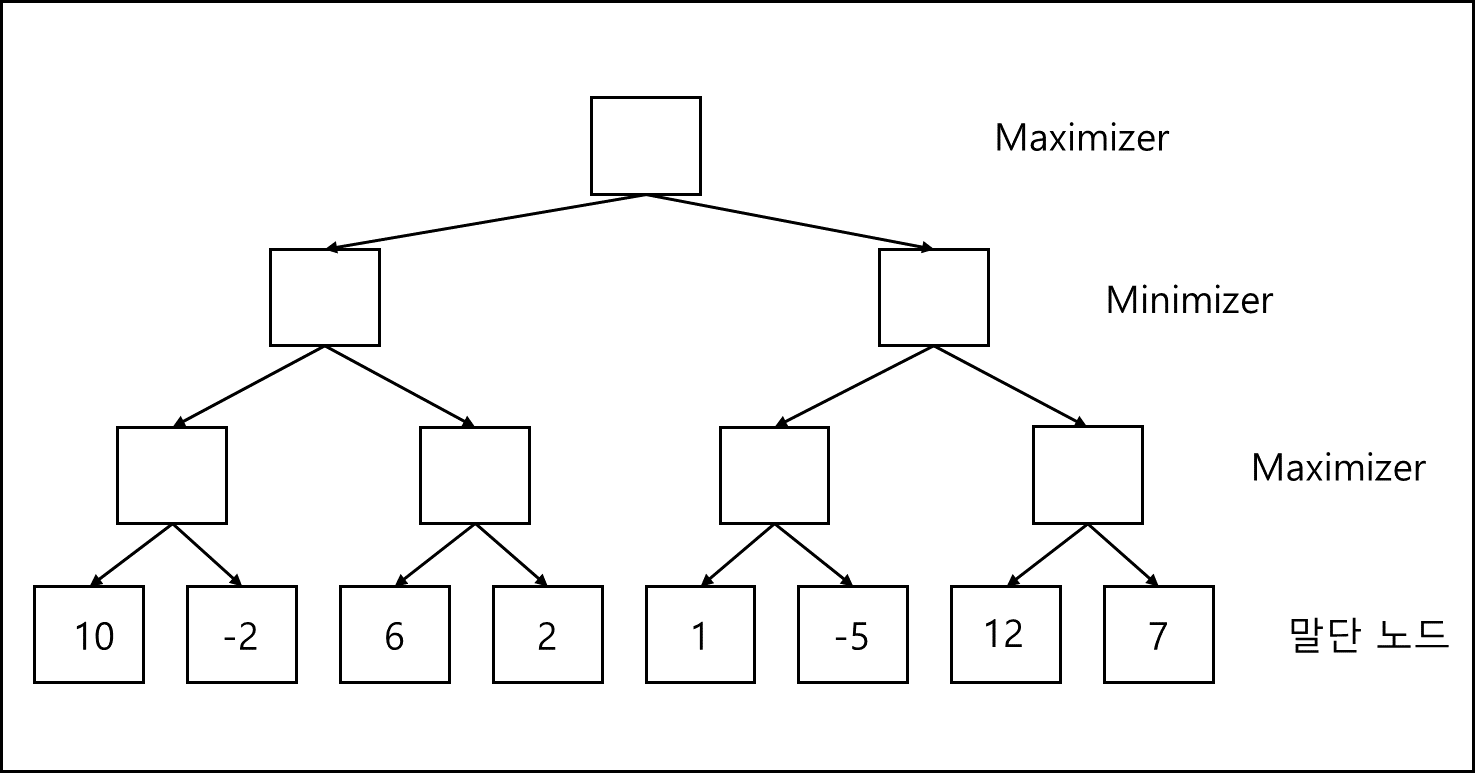
각각의 경우의 수를 탐색 트리로 구성하면 아래와 같이 된다.
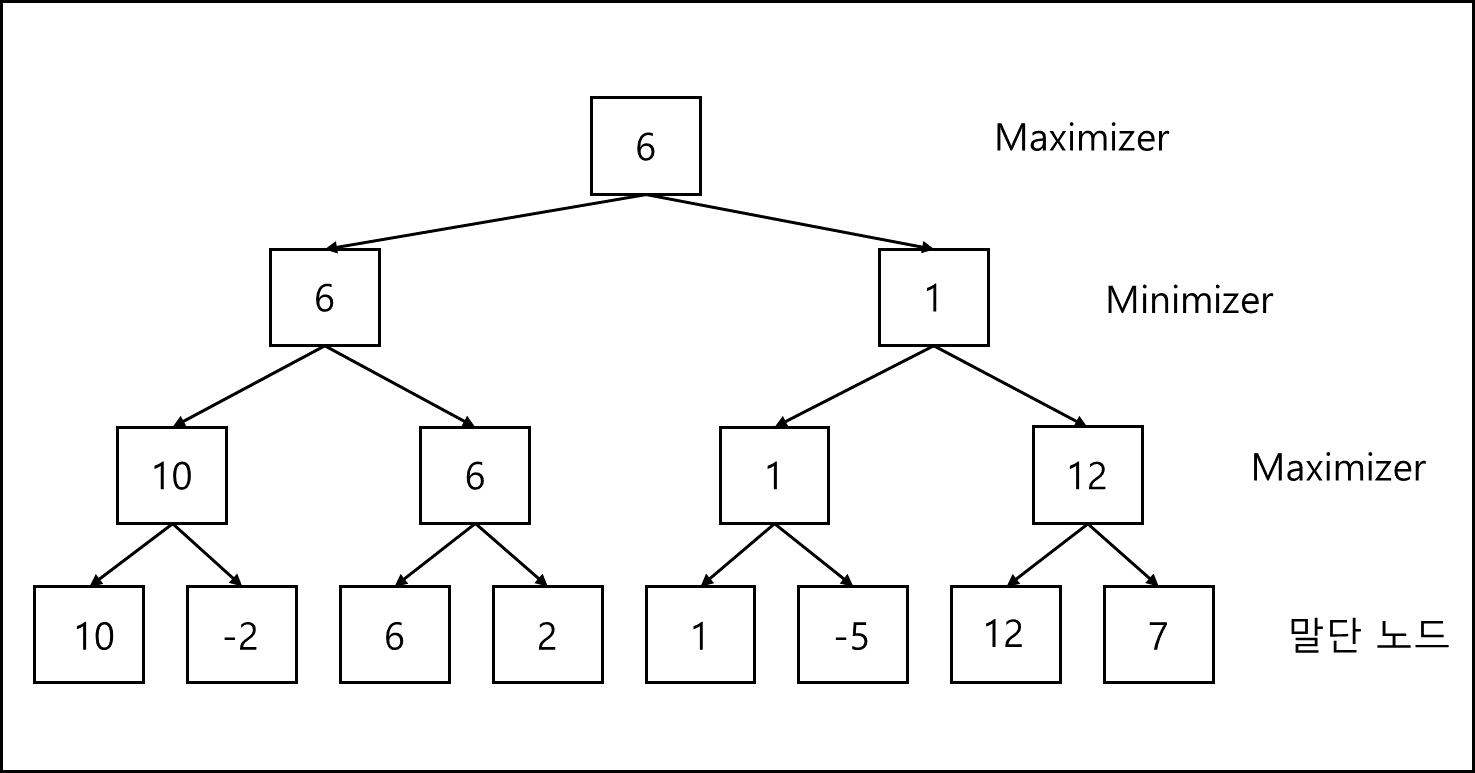
기본적으로 루트노드에서 DFS로 하나씩 탐색하여 리프노드에서 하나씩 탐색하며 부모노드로 값을 올리는데, 각각 턴마다 minimizer일때는 값을 최소로 올리고, maximizer는 값을 최대로 올린다. 따라서 위의 그림의 경우 결국에는 아래의 그림과 같은 형태가 된다.
이렇게 되면 전체의 모든 경우의 수를 늘어놓은 탐색 트리에서 가장 말단 노드의 평가함수 값을 찾아 올리는 방식으로 어떤 경우에서든 간에 가장 최적의 수를 선택 할 수 있다.
이렇게 탐색할 수 있으면 필승법이 있는 것 아니냐라고 할 수 있다. 틀린 말은 아니다. 모든 경우의 수를 다 파악할 수 있고 해당 부분에서 위의 탐색 트리와 같이 최상의 것만 취한다면 필승법은 항상 존재한다.
이론적으로만 봐선 이해하기가 어렵다.
따라서 예시를 들어 설명하도록 하겠다.
예시
Minimax 알고리즘을 설명할 때 많이 사용하는 게임인 틱택토 게임을 예시로 들어서 설명해볼까 한다. 틱택토 게임(Tic-tac-toe game)이란 3x3 판에서 O와 X를 서로 번갈아가면서 판에 긋는 게임으로 한 줄이 완성되면 이기는 게임이다.
평가 함수
Minimax 알고리즘을 쓰려면 평가함수에 의한 상황이 정의가 되어야한다. 틱택토 게임에서의 평가함수는 아래와 같다.
1
2
3
4
5
6
O을 Maximizer, X를 Minimizer라고 가정
최대 -9 ~ 9까지 가능하며 각 숫자는 이길 수 있는 경우의 수 개수를 나타냄
O측에서 이길수 있는 개수는 양수, X측에서 이길 수 있는 개수는 음수
양 측 값을 합산하여 평가 함수 값을 산정
0일 경우 먼저 두는 O 측에 유리하다고 판정
어느쪽에서 아예 이긴 경우(상대의 빙고 가능 횟수가 0) 해당 부호의 값으로 절대값 9를 반환
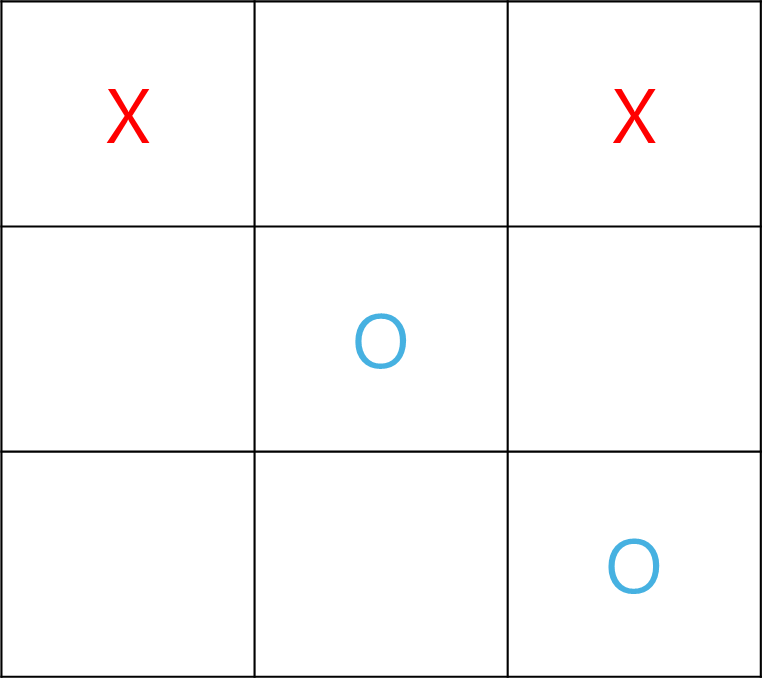
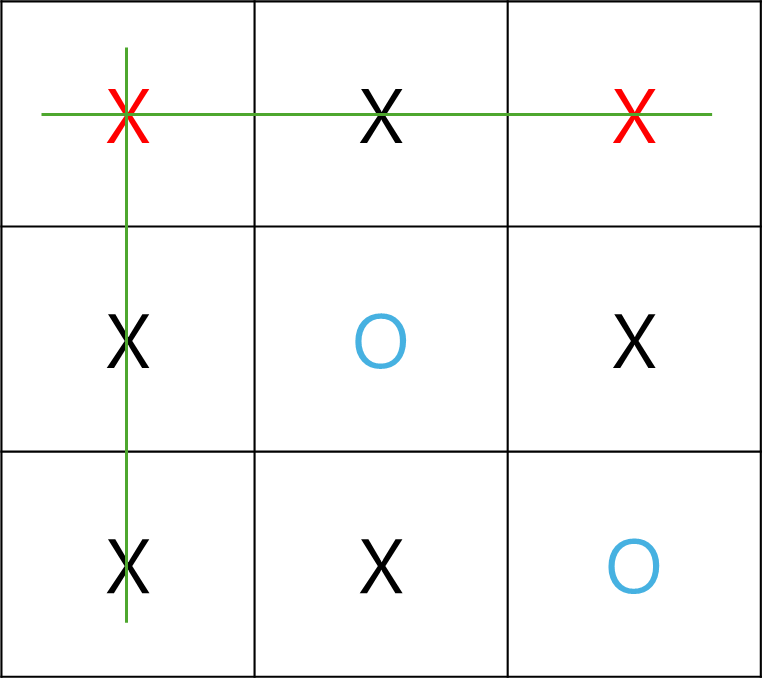
예를 들어보자 틱택토 게임간 아래와 같은 상황이라고 가정하자.
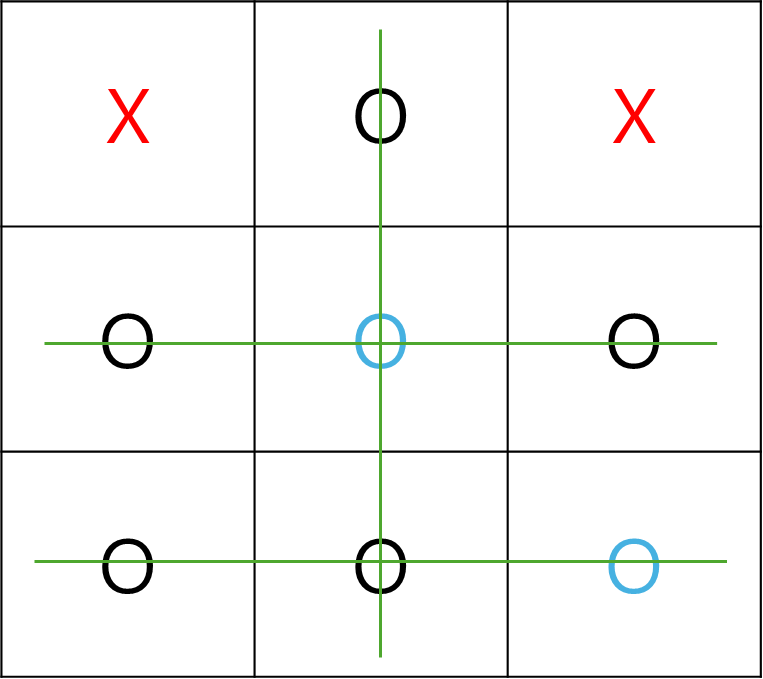
이 상황에서 O와 X에 대해 가능한 빙고의 수를 계산하여 각각의 값을 뺀다.
따라서 다음 경우의 평가 함수 값은 3-2=1이 된다.
연산 절차
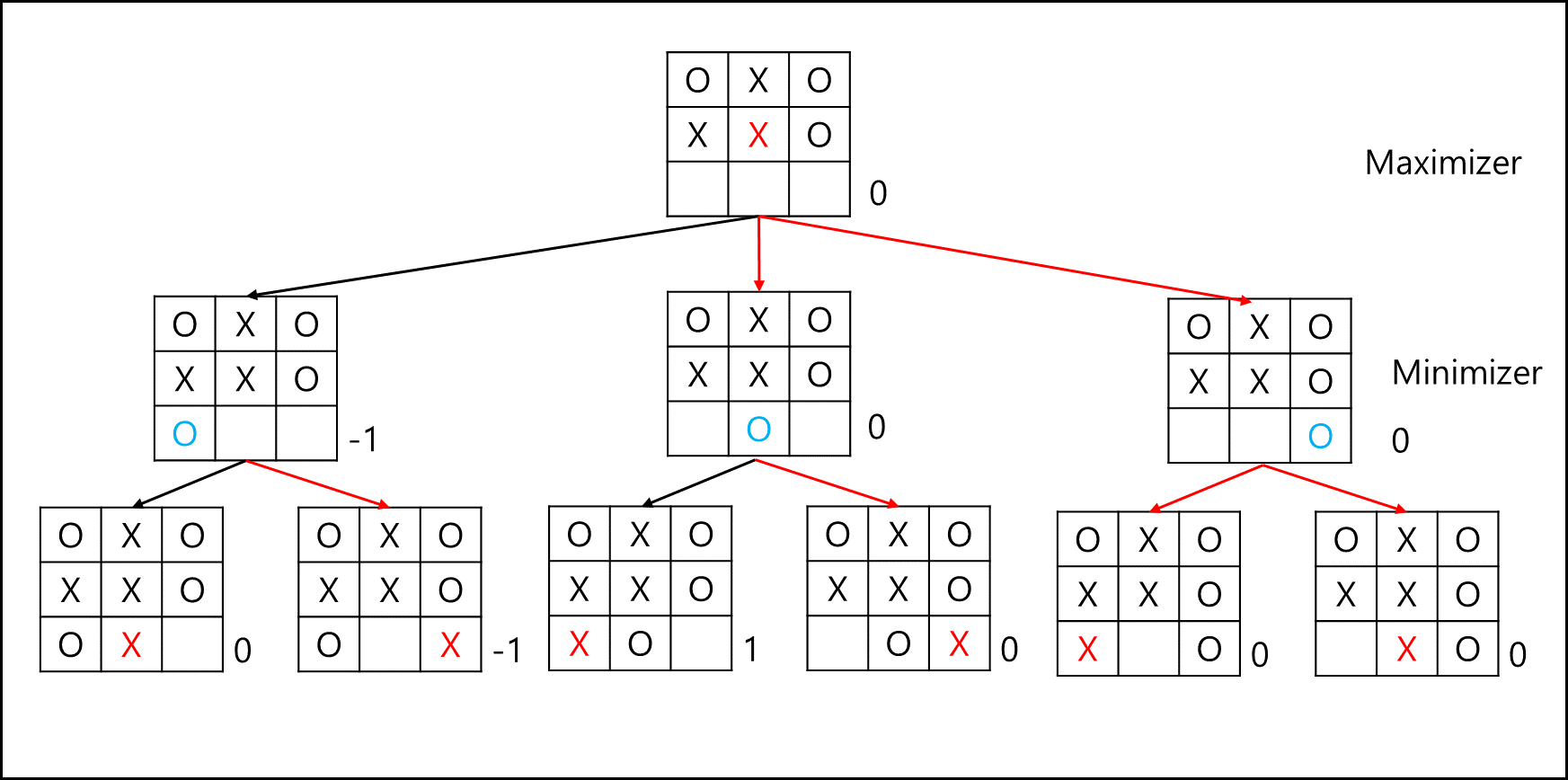
전체 탐색 트리는 너무도 크므로 부분만 갖고와서 설명하자면 아래와 같다.
Minimizer의 턴에서는 아래 노드에서 평가 함수가 작은 값을 선택하고 Maximizer의 턴에서는 아래 노드에서 평가 함수가 큰 값을 선택하므로 부모노드는 자식 노드에서 평가 함수 값을 갖고오는 식을 처리할 수 있다. DFS(Depth First Search)를 이용해서 자식 노드들을 탐색해서 부모노드의 평가 함수를 채울 수 있다.
따라서 전체 탐색 트리에서 가장 말단 노드부터 back-tracking하여 평가 함수 값을 지정하여 알고리즘 주체가 Maximizer일때는 평가 함수 값이 가장 큰 경우로, Minimizer일때는 평가 함수가 가장 작은 쪽으로 선택하면 항상 승리 할 수 있다.
정리
위의 설명까지만 보면 어떤 게임에서든 이길 수 있는 최상의 방식으로 보인다. 하지만 여기서 이야기하지 않은 것은 이런 게임의 경우 기본적으로 탐색 개수가 매우 많다는 것이다.
위 예시로 설명했던 틱택토 게임의 경우만 보더라도 모든 경우의 수는 9!= 9x8x7x6x5x4x3x2x1 = 362,880개이다. 이 정도는 컴퓨터로 충분히 돌릴만 하기 때문에 Minimax 알고리즘을 온전히 사용할 수 있지만 체스나 바둑과 같이 조금만 더 복잡한 게임으로 넘어가게 되면 탐색 해야하는 수가 기하급수적으로 커지기에 모든 경우의 수를 탐색하는 건 불가능에 가깝다. 따라서 탐색의 최대치를 제한하는 식으로 유한 시간내에 결과를 내는 방식을 택하며 이 최대치를 얼마나 늘리느냐에 따라
해당 알고리즘의 승률이 올라간다고 볼 수 있다.