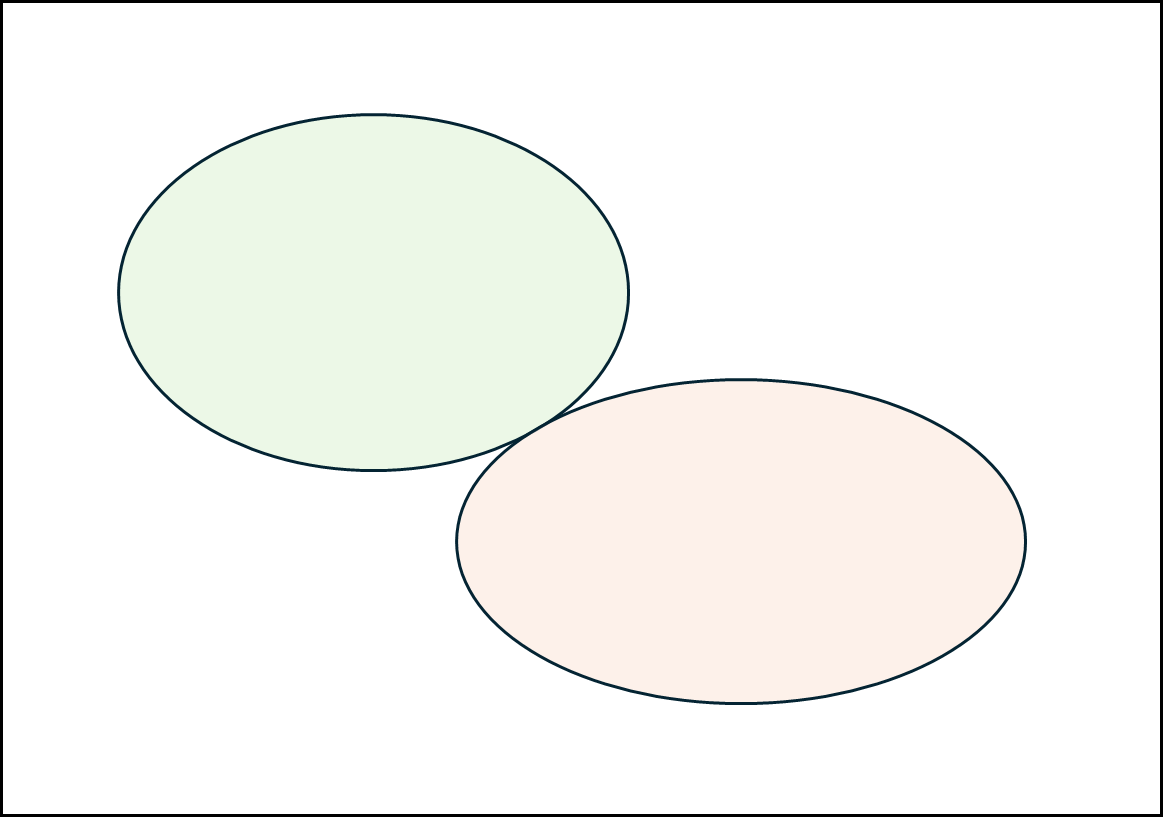공간 데이터 베이스 - 데이터 모델
공간 데이터 베이스 - 데이터 모델
1. 개요
모델이라고 하면 원래 건물을 지을때의 청사진이나 일종의 미니어처를 말한다. 하지만 여기서 앞에 데이터가 붙는다면 뜻은 좀 달라진다. 어떤 데이터 모음에 대한 구조나 형태를 말한다. 이 형태는 실질적으로 이 데이터가 어떤 역할을 하는지 설명에 대한 것도 붙는다. 전통적인 SQL DB에서 Column 이름을 설명에 가깝게 짓는것도 해당 이유때문이라고 할 수 있겠다.
이러한 데이터 모델을 잘 설계하는것은 매우 중요한데, 데이터 모델이 정립되어있다면 저장용량을 얼마나 사용할지 예측하기 쉽고 Query 성능에 대한 튜닝 및 측정이 매우 쉬워진다. 또한 다수의 응용에서 특정 공유 데이터를 재사용하기에 좋아지며 데이터 교환에 대한 편의성 역시 올라간다. 그렇다면 데이터 모델을 제대로 설계하지 못할 경우에는 반대의 경우가 일어나는 것인데, 간단한 예시로 Y2K 사태가 있다.
1999년에서 2000년도로 넘어가는 시점에서 표현이 저장 장치 및 여러 효율을 위해 99년도 같이 뒤에 2자리만 사용해서 정보를 다루고 있었는데, 이러한 시스템은 1960대에 설계되었었다. 그 당시에는 2000년 전까진 어떻게든 시스템을 바꾸겠지라는 생각때문에 안일하다면 안일한 생각으로 그렇게 설계한 것인데, 시스템이라는게 한번 구축되면 굉장히 보수적으로 운용하게 되기에 2000년 직전까지 그대로 사용하게 되었다.
그 당시만 하더라도 추상데이터 타입을 정의해두고 짰던게 아니라서 수정하는데 굉장히 큰 어려움을 겪었고 이는 그대로 비용문제가되어 많은 비용이 들었다.
다시 Y2K 같은 사태가 일어나지는 않을까?
일어난다. 이미 예정된 시기가 있다. Y2K38이라는 것인데, 서버시간을 표시할때 UNIX Timestamp이라는 정수형 int로 많이 저장한다.
이는 1970년1월1일부터 몇초가 지났는지 기재하는 방식이다. int가 표현 할수 있는 범위는 - 2^31 ~ 2^31이다.
이를 1970년1월1일부터 계산해보면 정수 오버플로우가 나타나는 시기는 2038년 1월 19일 3시 14분 7초이다. 이 후 오버플로우로인해 1901년 12월 13일이 되어버린다. 아마 64bit 타입 int로 바꾸던가 표기방식을 바꾸던가 해서 고쳐야할 것이다.
위와 같이 데이터 모델을 설계하는것은 중요하다. 이는 공간 정보 역시 마찬가지로 2가지 일반적인 모델이 있다.
2. 공간 정보 모델
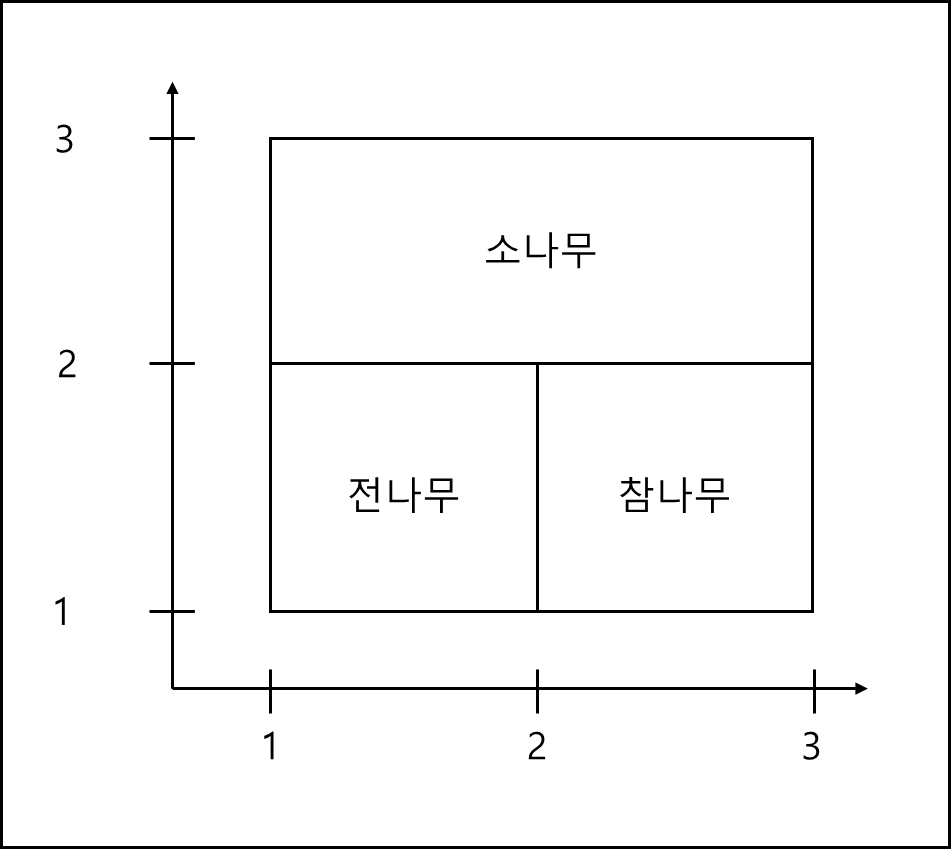
가령 아래의 그림과 같은 숲이 있다고 해보자, 일부는 소나무, 일부는 전나무, 일부는 참나무이다.
이를 그림이 아닌 모델로 표현하기 위해서는 아래와 같이 두 가지로 표현 할 수 있다.
1) 필드 기반
\(f(x,y) =\)
\(소나무: 1\le x\le 3, 2 \le y \le 3\)
\(전나무: 1\le x\le 2, 1 \le y \le 2\)
\(참나무: 2\le x\le 3, 1 \le y \le 2\)
공간을 연속적인 값의 함수(예: 고도, 온도)로 보기 때문에 위와 같이 함수로 표현 가능하다.
2) 객체 기반
| Area-ID | Dominant Tree species | Area/Boundary |
| 숲1 | 소나무 | [(0,2),(4,2),(4,4),(0,4)] |
| 숲2 | 전나무 | [(0,0),(2,0),(2,2),(0,2)] |
| 숲3 | 참나무 | [(2,0),(4,0),(4,2),(2,2)] |
공간을 도로, 호수 같은 식별 가능한 객체들(점·선·면)로 보기때문에 위와 같이 3개의 Polygon을 가진 형태의 객체 형태로도 만들 수 있다.
3. 공간 객체 모델
사실 객체가 뭐냐고 물으면 정의가 매우 애매하나, 일단은 각각에 대해서 식별가능해야하고 속성을 가지고 있으며 연산자가 포함되어있다는 점은 공통적이다. 이러한 기준을 가지고 공간 객체를 정의한다면, 공간 객체는 공간적 속성을 가지고 공간적 연산을 포함한 객체라고 할 수 있다.
공간 객체는 아래와 같은 계층을 이룬다. 아래의 계층 이름들은 각각 타입이다.
1
2
3
4
5
6
7
8
9
Geometry
├─ Point
├─ Curve (LineString)
├─ Surface (Polygon)
├─ Solid (3D) ← ISO 19107에서 다룸(3D 지원)
└─ GeometryCollection
├─ MultiPoint
├─ MultiCurve (MultiLineString)
└─ MultiSurface (MultiPolygon)
Geometry: 공통 속성(좌표계, 차원)과 공통 연산(엔벨로프, SRID getter 등)을 가진다. Point / Curve / Surface: 각각 0D, 1D, 2D(또는 3D) 원시(premitive). Simple Features는 주로 2D(꼭짓점은 선형 선분으로 보간) 중심으로 규정한다 Collections / Multi-*: 복수의 동일 타입(예: 여러 폴리곤)을 한 객체로 포장해 다루는 편의형.
이러한 공간 객체는 아래와 같은 속성을 가질 수 있다.
- 좌표와 SRID: 각 Geometry는 좌표를 갖고, 어떤 좌표계(SRID(Spatial Reference Identifier) / CRS(Spatial reference system))에 정의되었는지 명시한다. 서로 다른 SRID의 기하를 연산하려면 투영/변환이 필요하다.
- 차원성: 표준(특히 SFS)은 2D를 기본으로 하지만 Z(고도)나 M(측정값)을 포함하는 확장도 흔히 지원된다. ISO 19107은 3D(솔리드)도 다룬다.
또한 아래와 같은 연산을 가질 수 있다.
- 위상 술어(Topological predicates): Intersects, Contains, Within, Touches, Crosses, Disjoint 등 — 객체 간 위상 관계 판정.
- 거리/메트릭: Distance, ClosestPoint, Length, Area 등.
- 기하 연산(Constructive): Buffer, Union, Intersection, Difference, Simplify 등 — 새로운 Geometry를 생성.
- 기타: Envelope(MBR), Centroid, Boundary, IsValid(유효성 검사) 등
4. 위상 관계
위상 관계란 늘어나도(탄성 변형) 보존되는 관계를 말한다. (두 면이 접함과 같은 것)
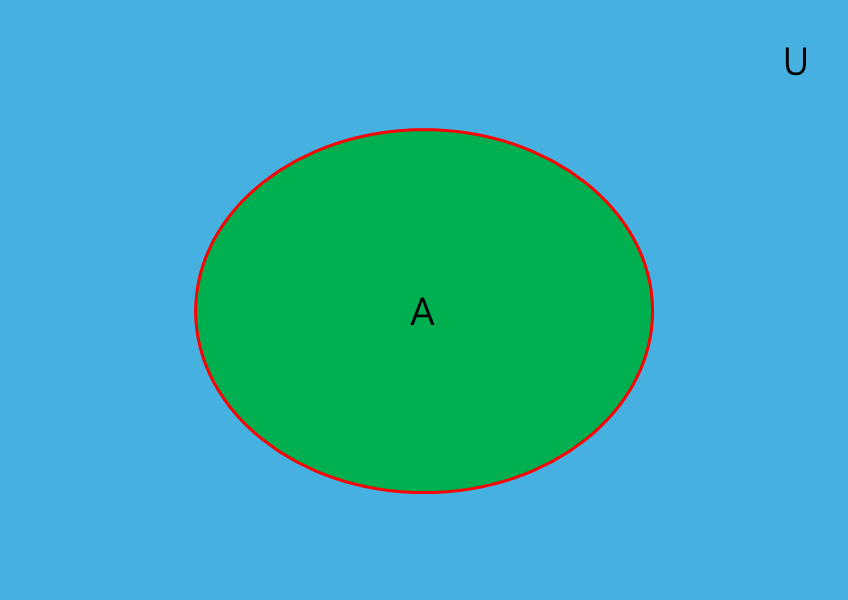
먼저 아래의 그림을 보자.
A 안을 차지한 초록색 부분 : $ A^{\circ} $
A 바깥의 U와 접한 빨간색 선 : $ \partial A $
U에서 A의 빨간선과 초록면을 제외한 부분 : $ A^{-} $
위와 같이 기호들을 정의할 수 있다.
이 기호들을 가지고 아래와 같이 Nine-Intersection model을 정의할 수 있다.
1) Nine-Intersection 모델
내부·경계·외부의 9개 교차로 위상 관계를 표현하는 것으로 여러 위상 관계를 3×3 Bool 행렬로 나타내는 것이다.
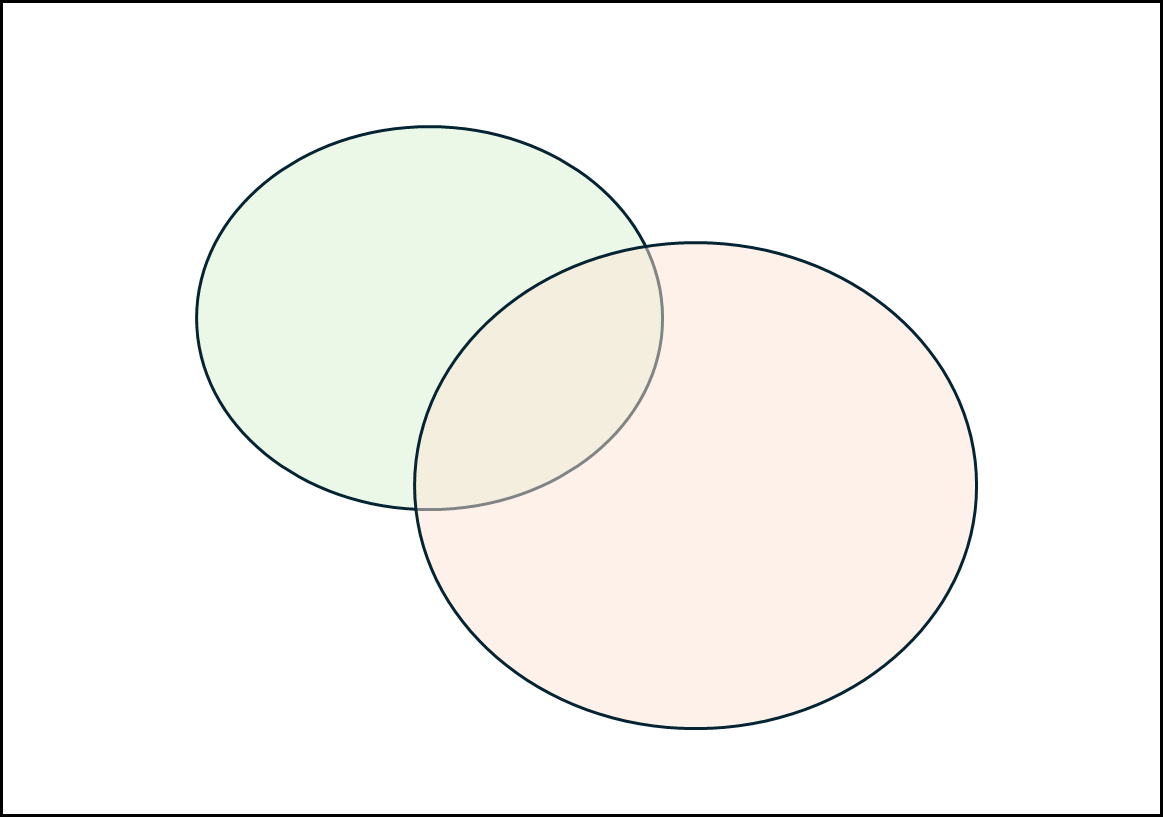
2차원을 표현하는 공간객체 A와 B가 있다고 할때, 이를 Nine-Intersection으로 표기하면 아래와 같다.
0이면 false과 1이면 true이다.
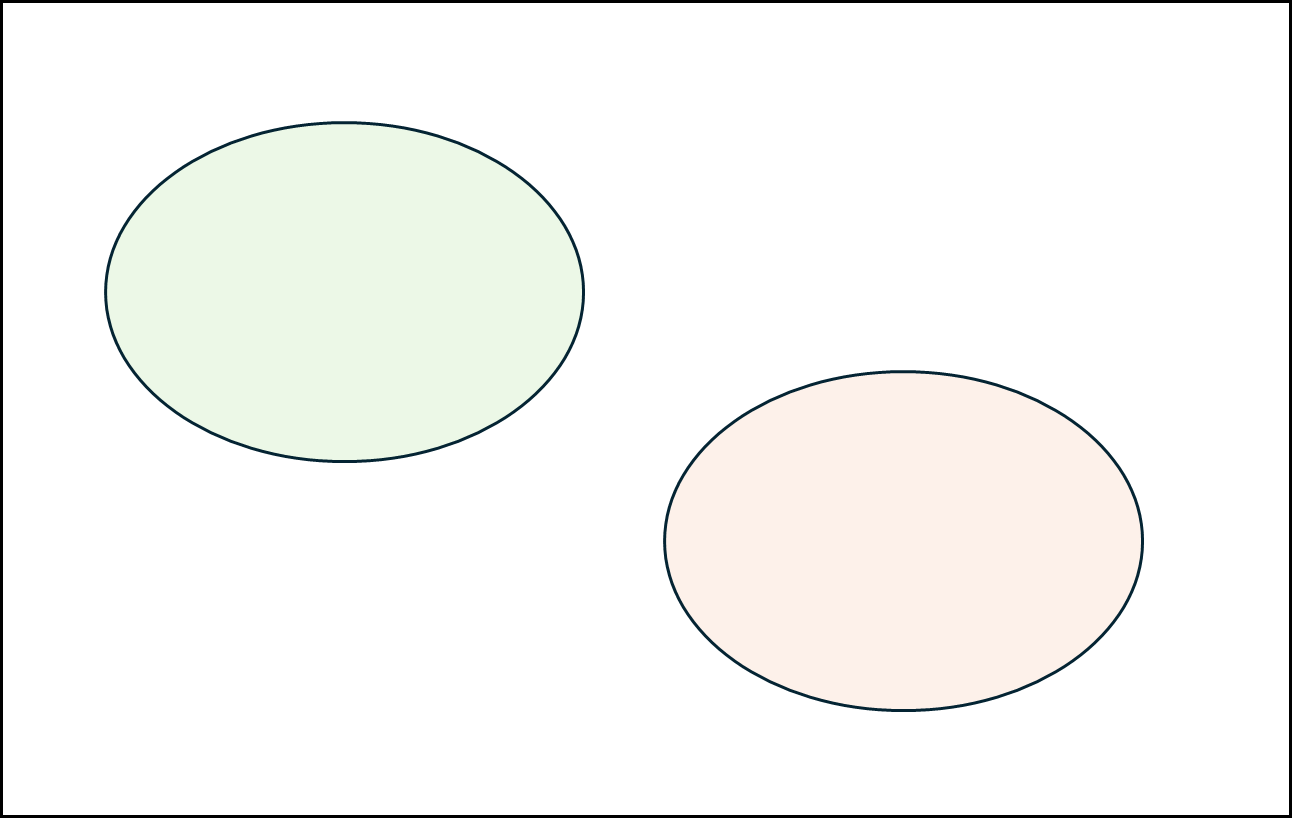
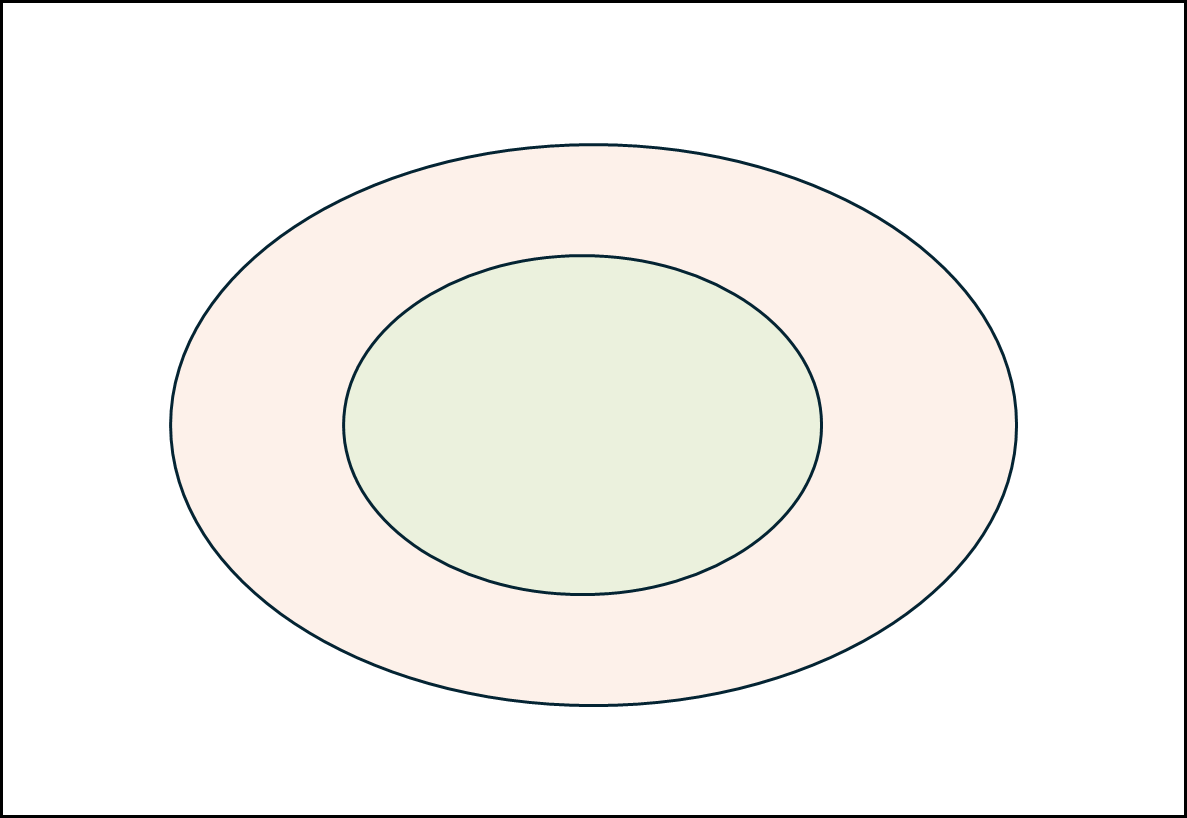
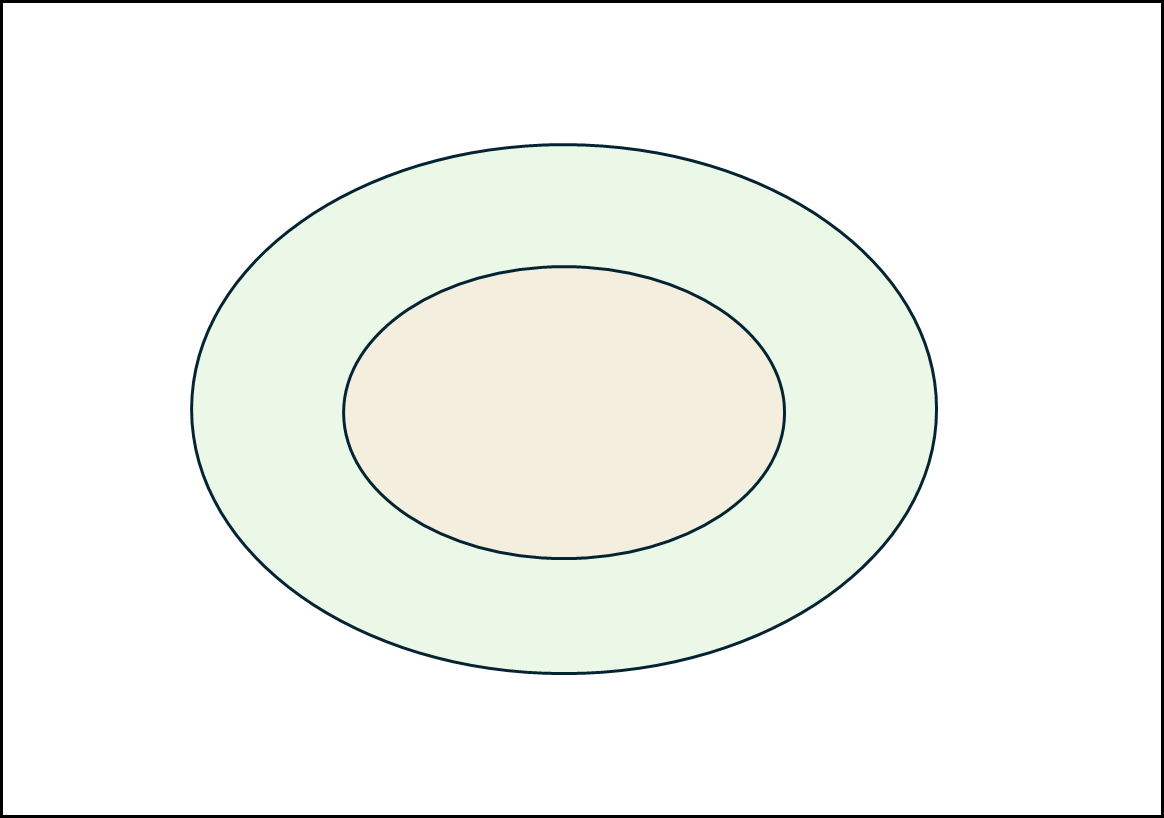
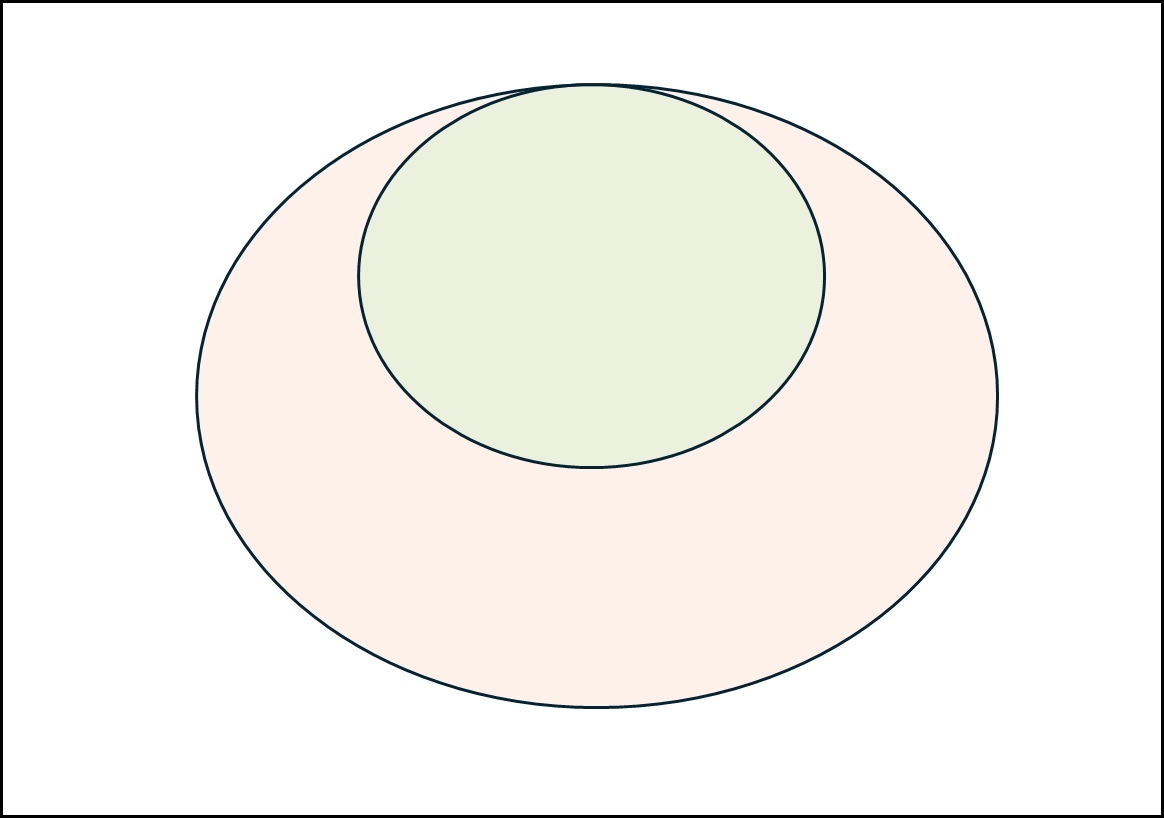
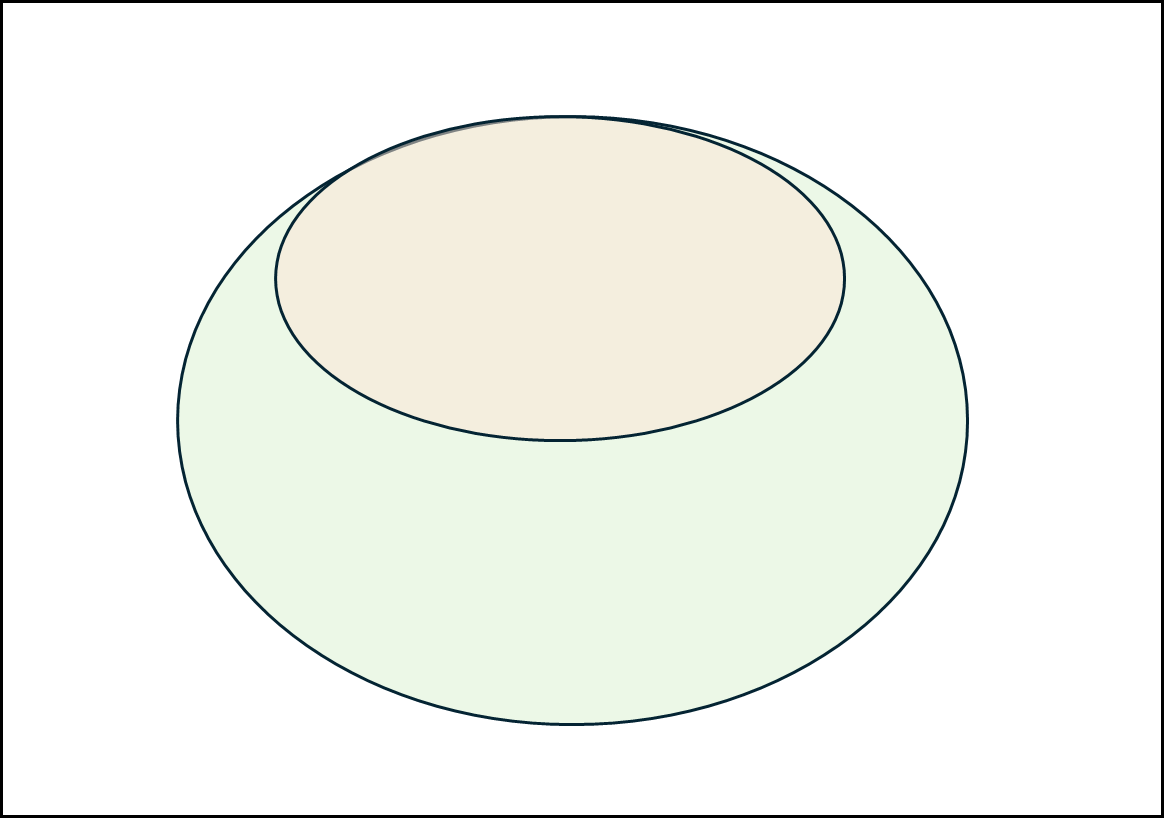
옅은 초록색이 A이고 옅은 주황색이 B라고 할때 위와 같은 행렬로 표현할 수 있는 것들을 아래와 같은 것들이 있다.
a. disjoint
b. contains
c. inside
d. equal
e. meet
f. covers
g. coveredBy
h. overlap
5. ER-Diagram for Spacial information
1) 공간 관계의 ER-Diagram 표현
관계형은 원자값만 허용하므로(폴리곤 같은 복합값은) 정점/엣지로 분해해 여러 테이블로 표현하게된다. 이때, 원자값만 허용하기 위해 일반적인 ER-Diaram의 형태와 조금 달리한다. 룰은 아래와 같다.
- 객체는 Relation으로 만든다.
- 한 개의 속성은 Relation의 열이된다.
- 다중값 속성은 새로운 Relation으로 만들되 객체의 Relation과 연결하는 외래키를 포함한다.
- 1:1, 1:N 관계는 외래키로 연결한다.
- M:N 관계는 Relation으로 만들되 참여 객체에서 외래키나 관계를 포함한다.
위와 같이 설명해두면 언뜻 봤을 때 이해가 잘 가지 않는데, 아래와 같이 예시를 두면 이해하기 쉽다.
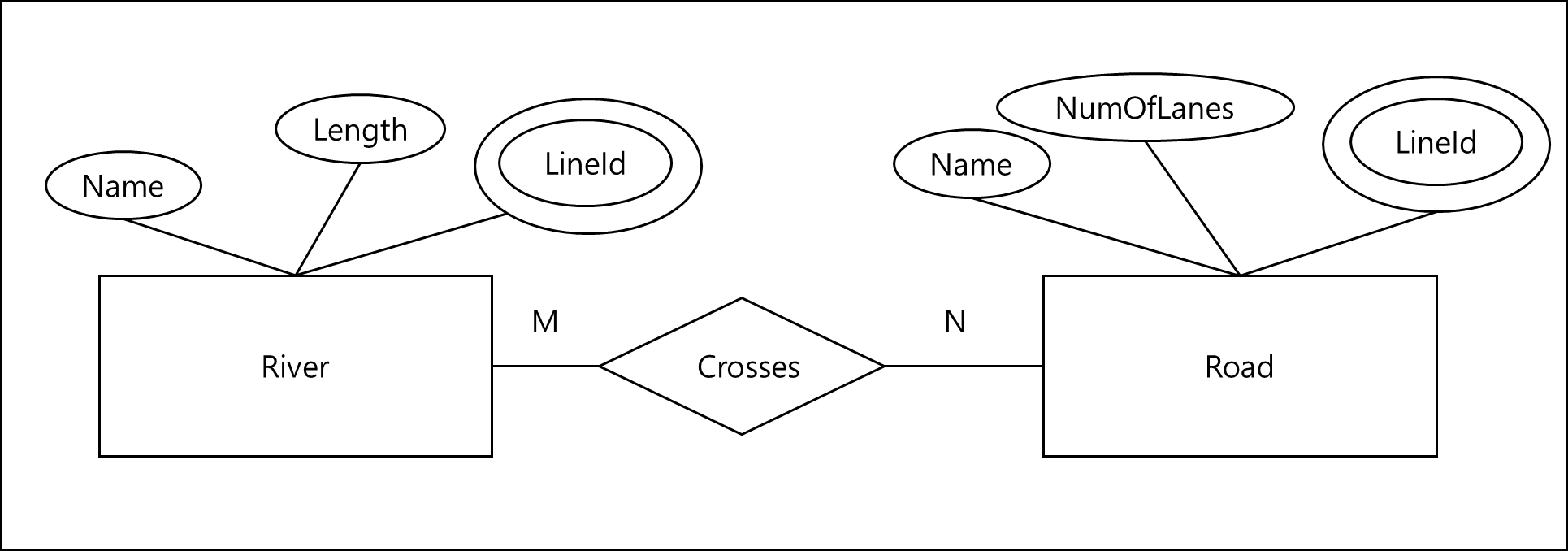
위의 그림은 강과 길에 대해서 ER-Diagram을 그려둔 것이다. 위 다이어그램을 테이블화하면 아래와 같다.
- River
| Name | Length |
| (varchar) | (Real) |
- Road
| Name | NumOfLanes |
| (varchar) | (Integer) |
- River-Crosses-Road
| RiverName | RoadName |
| (varchar) | (varchar) |
- Lines
| Lineid | seq-no | Pointid |
| (Integer) | (Integer) | (Integer) |
- Points
| Pointid | Latitude | Longitude |
| (Integer) | (Real) | (Real) |
각 객체의 한 개의 속성(Name, NumOfLanes)이라면 테이블 내의 한 개의 열로 정의되지만 다중 속성(Lineid)라면 별도의 테이블로 분리되
또한 각 객체 간의 M:N의 관계로 표현되는 것이라면 이 역시 별도의 테이블로 분리되어 각각의 Primary키로 연결하여 관계를 표현한다.
※ 공간 관계 예시
공간적인 객체에 대한 표현은 아래와 같이 하며 필요한 테이블끼리 Join해서 데이터를 표현한다.
- Polygon
| Polygonid | Seq-no | Pointid |
| (Integer) | (Integer) | (Integer) |
- Line
| Pointid | Seq-no | Pointid |
| (Integer) | (Integer) | (Integer) |
- Point
| Pointid | Latitude | Longitude |
| (Integer) | (Real) | (Real) |
- Elevation
| Name | PointID(FK) | Elevation |
| (varchar) | (Integer) | (Real) |
2) 공간 관계의 픽토그램화
공간 관계를 ER 다이어그램에 모두 그리면 복잡해지기 때문에 픽토그램으로 공간 타입(점·선·면·컬렉션)과 관계(파티션, 네트워크 등)를 표기하여 간결하게 표현하는게 좋다.
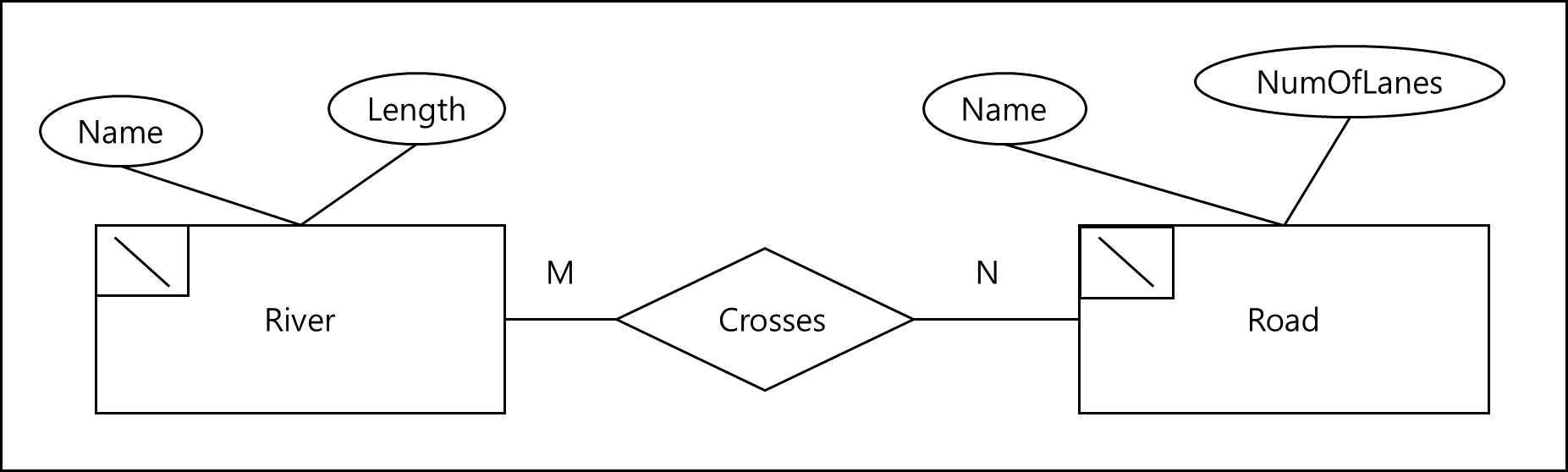
이전 예시를 가지고 픽토그램을 통해 표기하자면 각 객체 옆에 아래와 같이 표기할수있다.
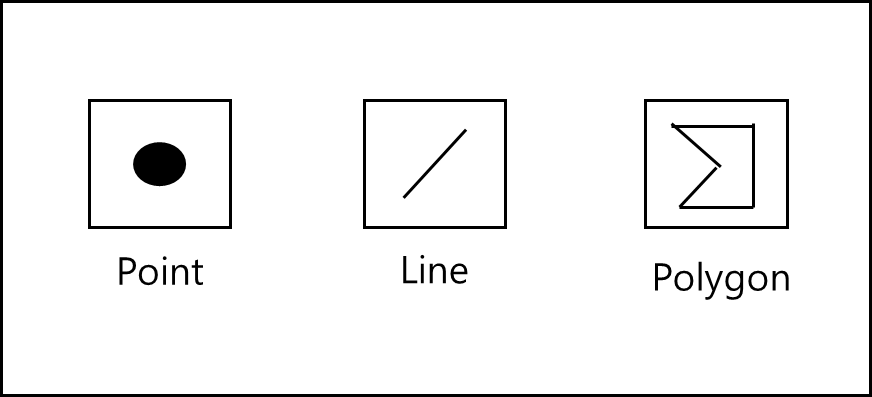
객체가 어떤 타입인지에 따라 표기법이 다른데, 아래는 표기법을 정리해둔것이다.
a. 기본 형태에 따른 표기법
b. Cardinality
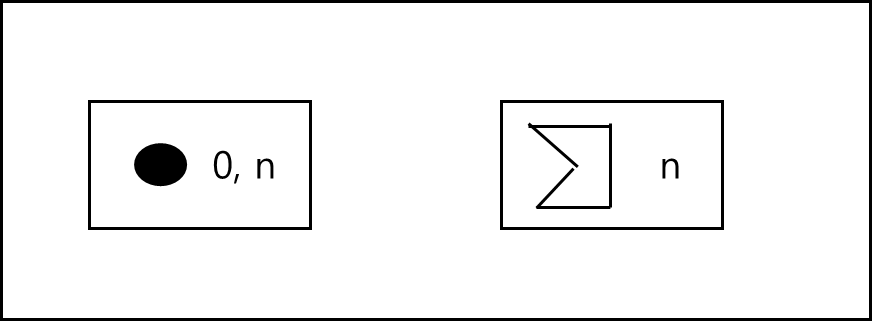
Cardinality의 경우 아래와 같은 종류가 있다.
- 0,1 : 있거나 1개이다.
- 1 : 1개이다.
- 1,n : 1개거나 다수개
- 0,n : 없거나 다수개
- n : 다수개
위의 종류를 각 객체에 표현하려면 아래와 같이 표현 가능하다.
해석하면 점이 없거나 다수개이다. Polygon이 다수개이다.
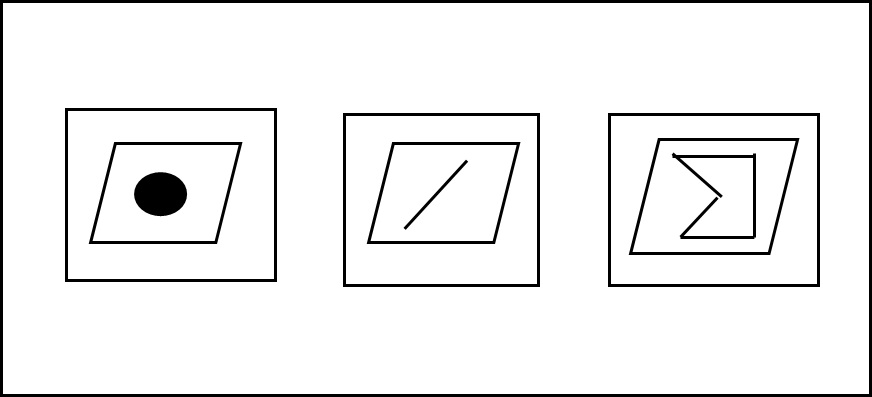
c. 파생된 형태
어떤 형태에서 파생된 형태를 표현하고 싶을 수 있다. 가령 미국의 주 경계 모양에서 미국의 모양을 도출한다던지 하는 경우를 말하는데 이럴때는 아래와 같이 표현 가능하다.
왼쪽부터 각각 점에서 파생함, 선에서 파생함, Polygon에서 파생함
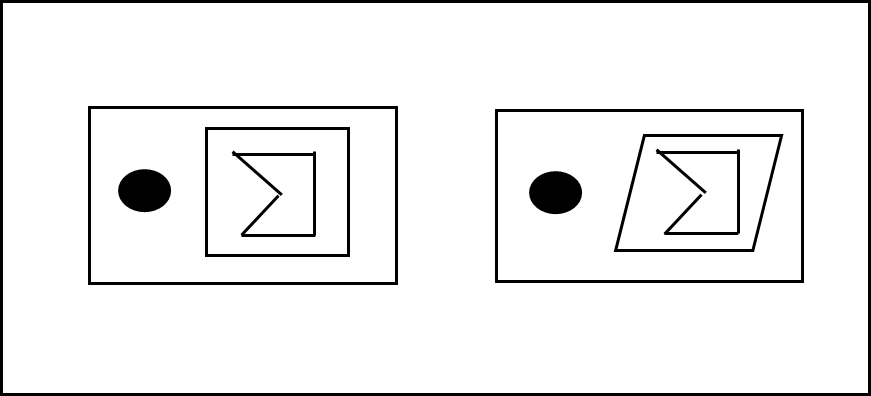
d. 대체 모양
양립 가능한 형태가 있을 수 있다. 어떤 도시의 경우에는 지도에서 Zoom-in 한 상태라면 Polygon으로 표기되겠지만, Zoom-out 한 상태라면 Point로 표기 가능하다. 이런 경우를 말한다.
왼쪽부터 점 혹은 Polygon 형태, 점 혹은 Polygon에서 파생한 형태이다.
참고자료
- Shashi Shekhar and Sanjay Chawla, Spatial Databases: A Tour, Prentice Hall, 2003
- P. RIigaux, M. Scholl, and A. Voisard, SPATIAL DATABASES With Application to GIS, Morgan Kaufmann Publishers, 2002
- INTERNATIONALSTANDARD-ISO19107 Geographic information — Spatialschema