공간 데이터 베이스 - Spatial Access Method
공간 데이터 베이스 - Spatial Access Method
이전 포스팅에서는 Spacial Query 종류가 어떤것이 있는지, 그리고 어떻게 사용하는지 예시를 알아보았다. 이번에는 어떤식으로 해당 쿼리들을 구현하는지에 대해 알아볼까 한다.
1. 개요
우리가 일반적으로 사용하던 SQL DB에서 일반적인 타입의 경우에는 값을 찾아오기에 매우 쉬운 편이다.
숫자 타입이라면 크고 작음을 비교할 수 있고, 사실 문자열의 경우에도 사전 배열식으로 정렬하면 크고 작음을 비교 할 수 있기 때문에 B+ 트리의 혜택을 받아 전체 정렬(Total Ordering)이 가능하다. 즉, 어떤 값을 뽑아서 대소를 비교할 수 있기 때문에 해당 Column에 대해서 Index만 걸려있다면 $log_{m}N$ (M은 차수, N은 총 개수) 내에 찾을 수 있는 것이다.
하지만 공간 데이터의 경우 좀 애매하다.
어떤 2차원 공간에서 좌표간의 대소를 비교하기엔 좀 어렵다. 물론 X와 Y로 나누어서 별도로 비교할 수는 있겠지만 그렇다고 X와 Y로 나누어서 별도로 INDEX를 걸어봐야 찾기 더 어려워질 뿐이다.
아래와 같은 어떤 Polygon이 있다고 해보자.
해당 Polygon안에 어떤 점이 포함되어있는지 알고 싶다고 할때 여기서 공간 데이터 베이스에서는 인덱스를 어떻게 처리하면 좋을까? 여기서 등장하는 것이 필터와 정밀검사 두 단계이다.
2. 인덱스 방식
※ MBB(Minimum Bounding Box) or MBR(Minimum Bounding Rectangle)
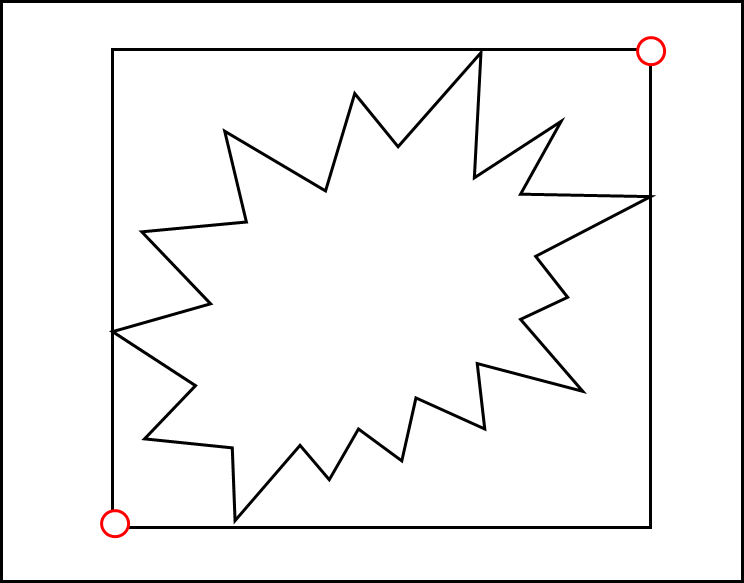
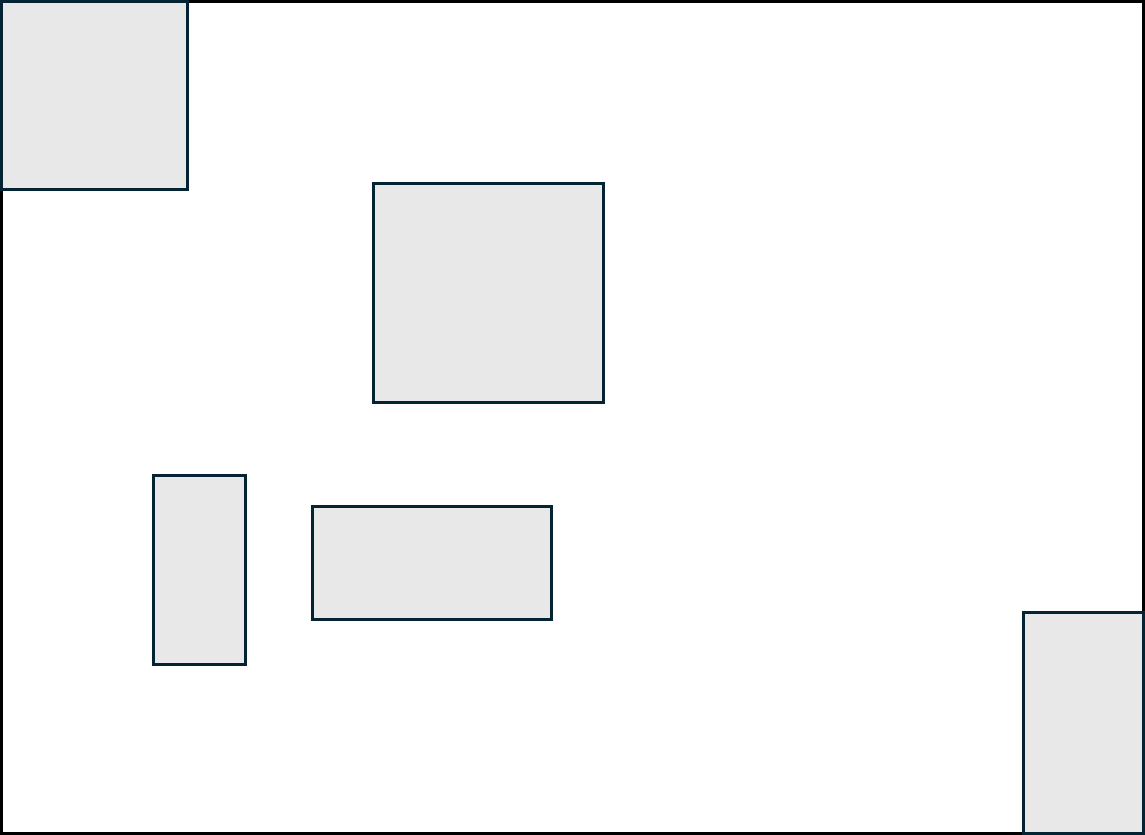
처음에 Polygon이 추가되고 Indexing 될 때 해당 Polygon에 대해서 minimum bounding rectangle 혹은 minimum bounding box(이하 mbb) 라고 불리는 박스를 만든다. 이는 해당 Polygon이 아래와 같이 딱 들어 맞는 사각형을 말한다.
위와 같은 mbb는 우측 상단과 좌측 하단에 있는 빨간 점과 같이 2개의 점으로 표현 가능하다.
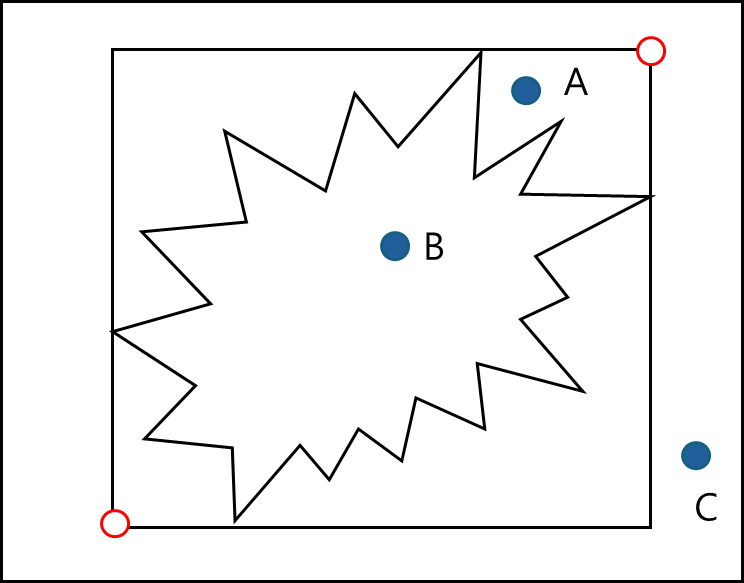
DB는 해당 Polygon 안에 포함된 점을 찾을 때 저 빨간 2개의 점을 이용하여 범위로 Search가 가능하다.
위와 같은 점들이 있을 때 C는 확실히 배제하고 시작할 수 있는 것이다.
그 와중에 사각형 내에는 포함되어있으나 실제 포함되어있는지 여부를 확인하기 위해 A,B 점은 실제 기하 구조에 대해서 확인을 해야하는데, 이 과정에서 탈락되는 객체를 false drop이라고 부른다.
false drop이 적을 수록 실제 정밀 검사를 해야할 대상이 줄어드는 것이다.
꼭 인덱스를 mbb 같은 사각형으로 하지 않아도 괜찮다. 하지만 사각형 같이 근사(Approximate)한 구조체가 복잡할 수록 인덱스의 유지 비용과 검색 비용이 올라간다.
1) Space-Driven Structure
a. 고정 그리드(Fixed Grid)
공간을 균등한 크기의 nx × ny Cell로 나눈다. 각각의 셀은 Disk Page와 연관되어있으며 포인트 P가 어떤 Cell안에 포함되어있다면 포인트 P는 해당 Cell안에 있으며 해당 Disk Page에 포함되어있다.
각 포인트는 어떤 Cell에 포함되어있는지 알 수 있으며 해당 Cell을 해당 Page에서 불러오면 값을 읽어올 수 있다. 만약에 다수의 Cell에 대해서 연관되어있다면 대상 Cell들과 연결되어있는 모든 Page를 불러와서 처리해야한다.
만약 셀 크기를 잘 못 잡으면 특정 Cell로 많은 포인트가 몰려서 Overflow(해당 페이지에 모두 기재할 수 없는 경우)가 발생 할 수 있으며 만약 Point 자체도 각 셀에 균일 분포되어있는게 아니라 한 셀에 다수가 몰려있는 비균일 분포라면 성능이 저하 될 수 있다.
b. Grid File
Grid File은 각 축(x, y, …)에 대해 분할 경계(scale)를 관리하는 적응형 격자 디렉터리와 실제 데이터(버킷/페이지)를 분리해서 저장한다. 디렉터리의 각 셀은 물리적 데이터 페이지(버킷)를 가리키며, 여러 디렉터리 셀이 같은 데이터 페이지를 참조할 수 있어 공간을 절약한다. 삽입 시에는 Overflow가 난 셀만 국소적으로 분할하고, 필요하면 디렉터리(또는 스케일)를 확장한다.
이렇게만 들으면 이해가 잘 가지 않는다. 아래의 예시를 보자.
※ 예시
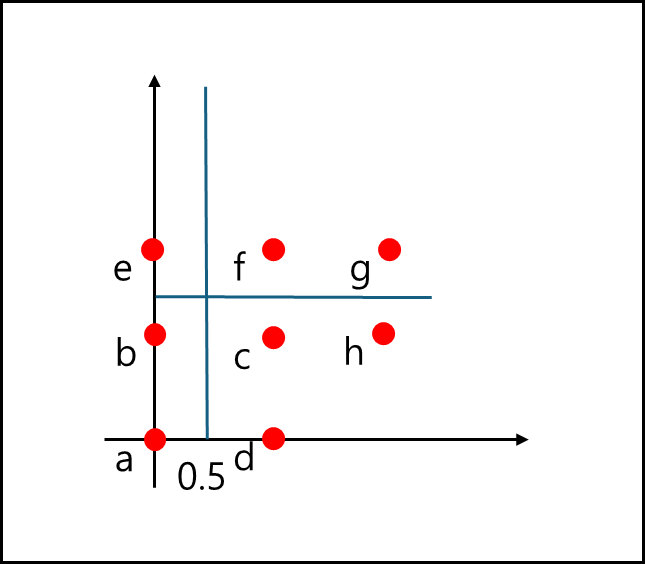
입력값이 a(0,0), b(0,1), c(0,1), d(0,1), e(0,1), f(0,1), g(0,1), h(0,1), i(0,1)이고 순서대로 추가된다고 가정 해보자.
기본적으로 x와 y에 대한 스케일은 Sx=[∞], Sy=[∞] 이다.
Pn은 페이지 넘버이고, DIR[N,M]이 가로로 N번째 세로로 M번째 디렉토리 셀이라고 할때
각 물리적 페이지에 총 3개씩 Point가 들어갈 수 있다고 하면 입력값이 하나씩 추가됨에 따라 디렉터리의 변화와 페이지의 변화는 아래와 같다. 디렉토리 분할이 일어나지 전까지는 그림을 통합하여두었다.
a 입력
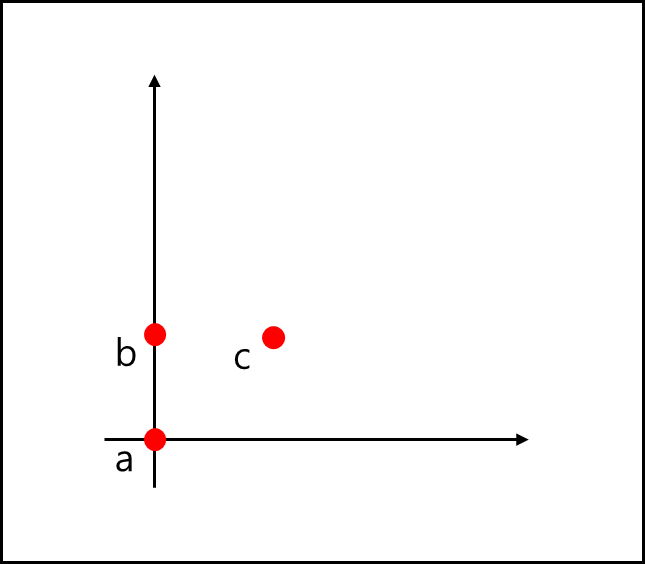
P1 = a, DIR[1,1]=P1 이다. 페이지당 3개 초과가 아니기 때문에 분할은 일어나지 않는다.b 입력
P1 = a,b DIR[1,1]=P1 이다. 페이지당 3개 초과가 아니기 때문에 분할은 일어나지 않는다.c 입력
P1 = a,b,c DIR[1,1]=P1 이다. 페이지당 3개 초과가 아니기 때문에 분할은 일어나지 않는다.
d 입력
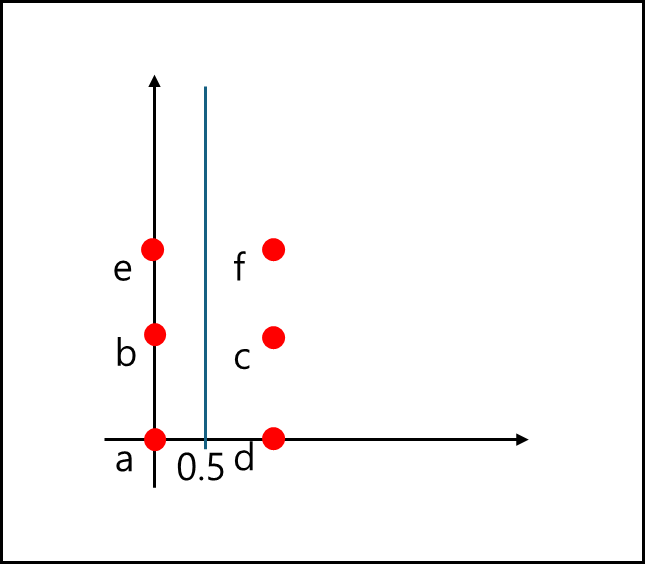
한 페이지에 3개를 초과하므로 분할이 일어난다. y축에 평행하게 거리의 중간 값으로 나누게 된다면 0.5를 기준으로 나누게 되며
때문에 Sx=[0.5,∞], Sy=[∞] 가 된다. 또한 물리 페이지 역시 분할해야되기 때문에 P1 = a,b, P2 = c,d DIR[1,1]=P1, DIR[2,1]=P2 이다.e 입력
각 페이지별로 3개 초과가 아니므로 page에 포인트만 추가되고 그대로 유지된다.
Sx=[0.5,∞], Sy=[∞]에 P1 = a,b,e , P2 = c,d DIR[1,1]=P1, DIR[2,1]=P2 이다.f 입력
각 페이지별로 3개 초과가 아니므로 page에 포인트만 추가되고 그대로 유지된다.
Sx=[0.5,∞], Sy=[∞]에 P1 = a,b,e , P2 = c,d,f DIR[1,1]=P1, DIR[2,1]=P2 이다.
g 입력
한 페이지에 3개를 초과하므로 분할이 일어난다. x축에 평행하게 거리의 중간 값으로 나누게 된다면 1.5를 기준으로 나누게 되며
Sx=[0.5,∞], Sy=[1.5,∞]에 P1 = a,b,e , P2 = c,d , P3=f,g DIR[1,1]=P1, DIR[2,1]=P2, DIR[1,2]=P1 ,DIR[2,2]=P3 이다.h 입력
각 페이지별로 3개 초과가 아니므로 page에 포인트만 추가되고 그대로 유지된다.
Sx=[0.5,∞], Sy=[1.5,∞]에 P1 = a,b,e , P2 = c,d,h , P3=f,g DIR[1,1]=P1, DIR[2,1]=P2, DIR[1,2]=P1 ,DIR[2,2]=P3 이다.
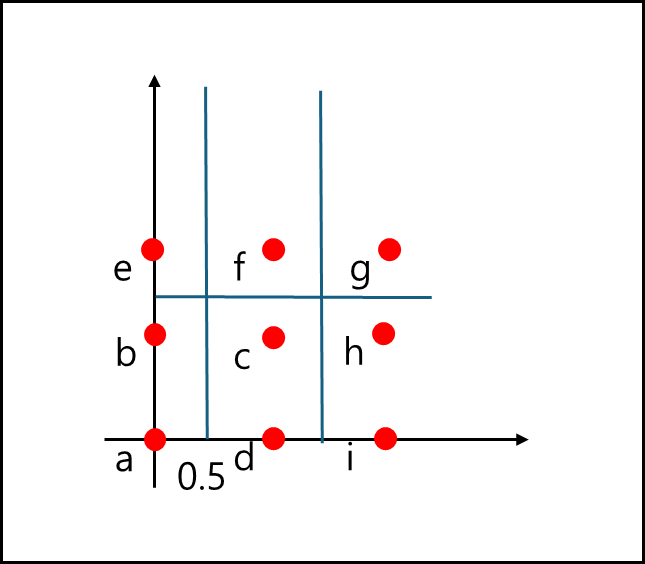
- i 입력
한 페이지에 3개를 초과하므로 분할이 일어난다. y축에 평행하게 거리의 중간 값으로 나누게 된다면 1.5를 기준으로 나누게 되며
Sx=[0.5,1.5,∞], Sy=[1.5,∞]에 P1 = a,b,e , P2 = c,d , P3=f,g, P4=h,i, DIR[1,1]=P1, DIR[2,1]=P2, DIR[1,2]=P1 ,DIR[2,2]=P3, DIR[3,1]=P3 , DIR[3,2]=P3, 이다.
※ 삽입시 세가지 케이스
위 예시를 보면서 총 세가지 케이스로 처리되는 것을 알 수 있었을 것이다. 이를 정리해보면 아래와 같다.
A. No cell split
대상 페이지에 여유가 있으면 단순히 삽입하면 된다.B. Cell split, but no directory split
대상 버킷(페이지)에 삽입시에 용량이 넘치면 그 셀을 분할(어느 축을 쪼갤지 결정)한다. 분할은 한 축(x 혹은 y)에서 경계 하나를 추가(스케일 배열에 값 삽입)해서 디렉터리의 일부 엔트리들이 새로 생성된 버킷을 가리키도록 하며 디렉터리 자체(메모리 구조)의 크기는 동일하지만, 해당 행/열의 엔트리들이 새 버킷 포인터로 변경될 수 있다.C. Cell split and directory split
분할하려는 셀이 디렉터리에서 여러 엔트리의 공유 대상(즉 디렉터리의 포인트 수용량이 충분하지 않을 때)인 경우, 스케일 배열 갱신이 디렉터리의 차원을 실질적으로 ‘늘려야’ 할 수 있다. 이때 디렉터리를 확장 또는 재생성(일부 복제)해야 하며, 일반적으로 디렉터리의 행/열을 반복 복제하거나 더 세밀한 인덱스를 만들게 된다. 구현상 디렉터리 분할은 비용이 크므로 드물게 발생하도록 설계(버킷 분할 전략, 축 선택 규칙 등)를 조정한다.
c. Linear Quadtree(선형 쿼드 트리)
기본적으로 2차원 공간을 재귀적으로 4분면으로 분할하며 공간 안의 객체의 밀도를 조절하는 방식이다.
요컨대 각 사분면에 겹치는 사각형이 페이지 용량 미만이 될 때까지 4분면으로 나누는 방식이라고 할 수 있다.
처음에 4분면으로 나눠진 사분면들 안의 객체 개수가 크기가 넘는다면 다시 4분할 한다. 이를 재귀적으로 분할하면 특정 부분은 크게 남고 몇개는 작게 나눠진다. 각 사분면의 부여된 인덱스(인덱싱 방법은 아래 참조)를 기준으로 리프노드의 부모 노드를 만들고 최종 사분면들은 리프노드로 구성되어 해당 사분면이 포함한 객체의 MBB 값과 Page 주소를 포함하고 있다. 때문에 비교적 빠른 속도로 filtering이 가능하다.
① 인덱싱 방법
- Z-order(Morton code)
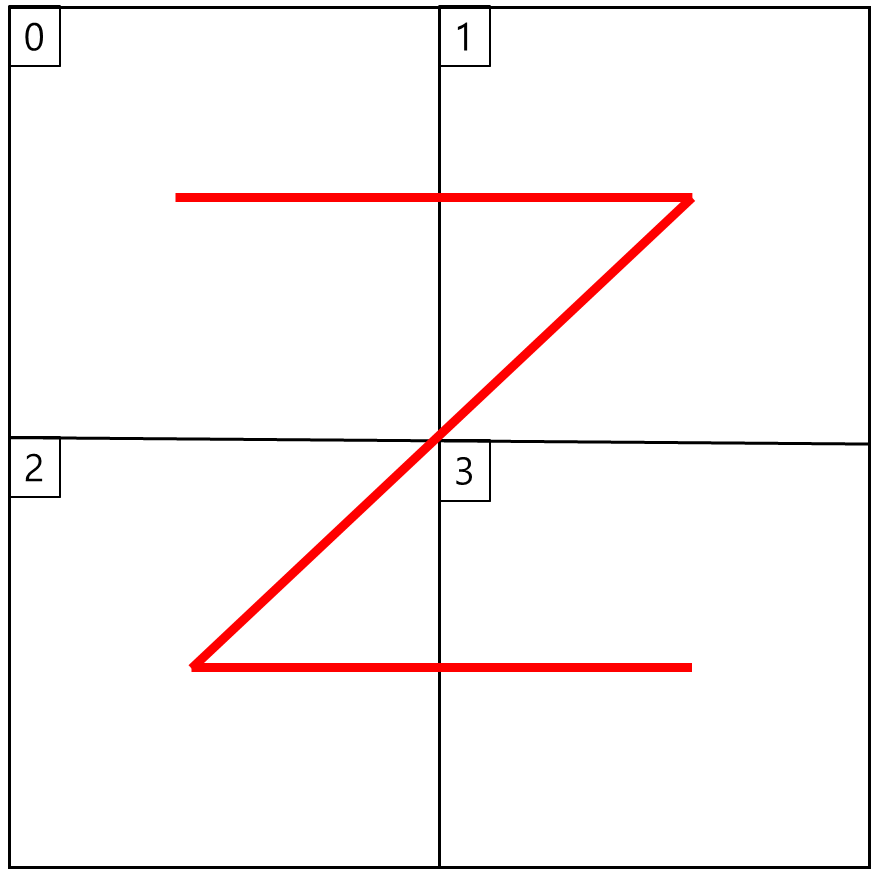
순서를 Z 모양으로 구성한다고 해서 Z-order이다. (Morton code라고도 한다)
어떤 2차원 평면이 있다고 할 때 4분면으로 나누면 아래와 같은 그림으로 순서를 잡는다.
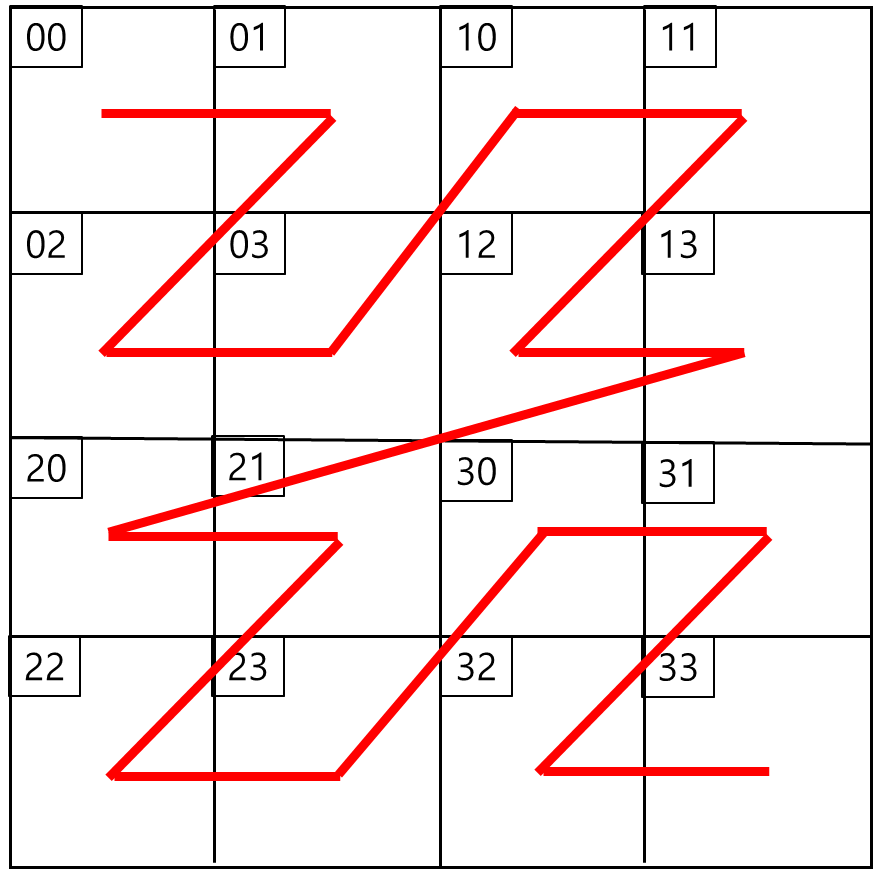
만약 4개가 아닌 각각의 사분면에 한번 더 잘릴 경우 아래와 같다.
위와 같이 계속해서 Z 형태로 연속해서 순서를 부여한다. 이때 순서에 대한 문자는 사전식 정렬(Lexicographical Order)을 따르며 이 순서를 기준으로 B+ tree에 Mapping한다.
이러한 Z-order는 키 계산이 Hilbert curve 보단 단순해서 연산 리소스를 크게 잡아먹진 않는다.
하지만 2차원 평면 상에서 데이터가 가까울 경우에 1차원 인덱스까지 가깝진 않은데 이는 검색시에
쓸데 없는 데이터까지 갖고오는 문제를 초래할 수 있다.
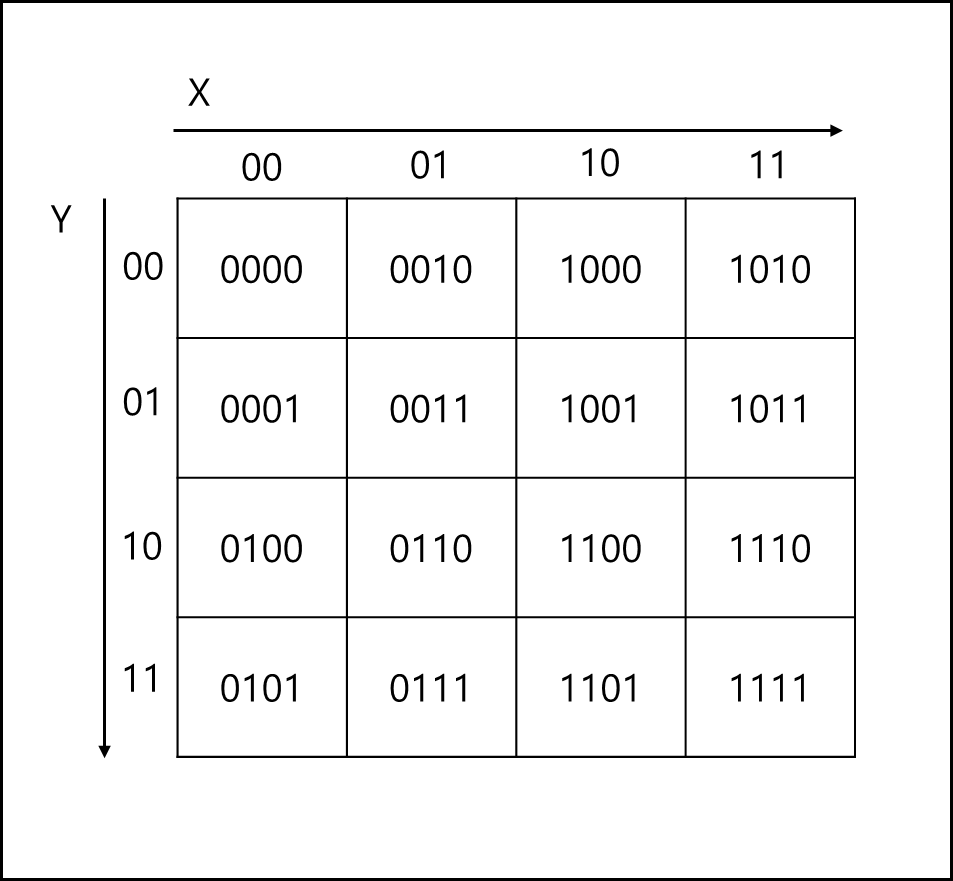
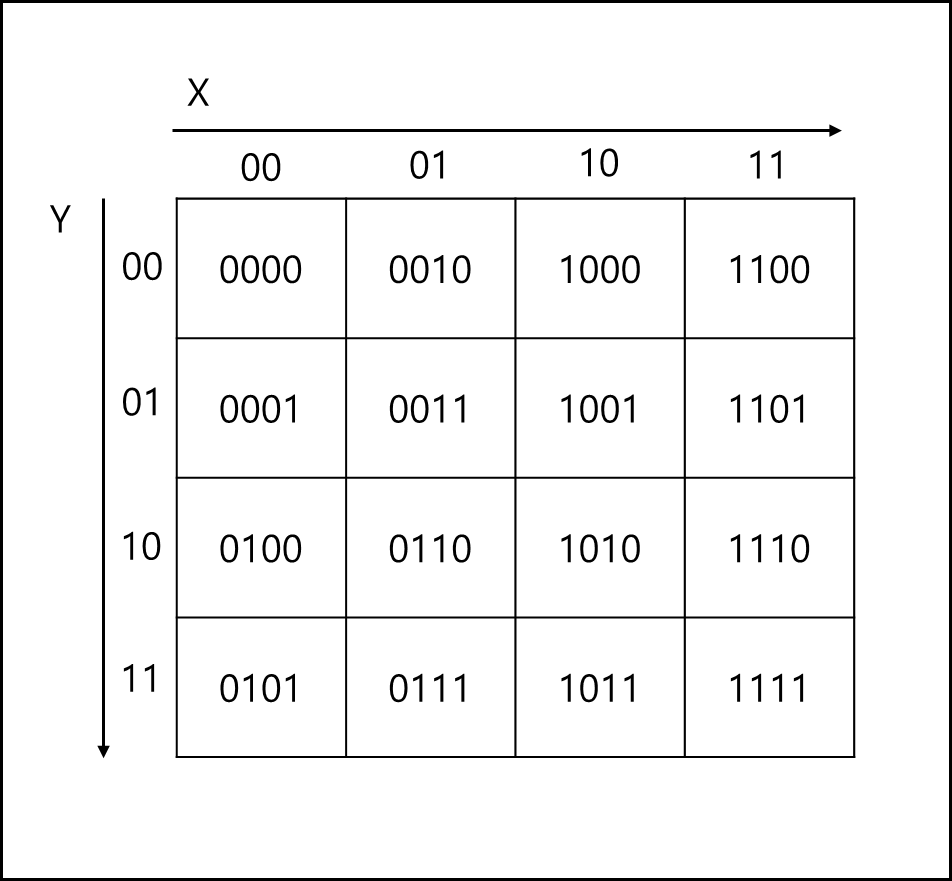
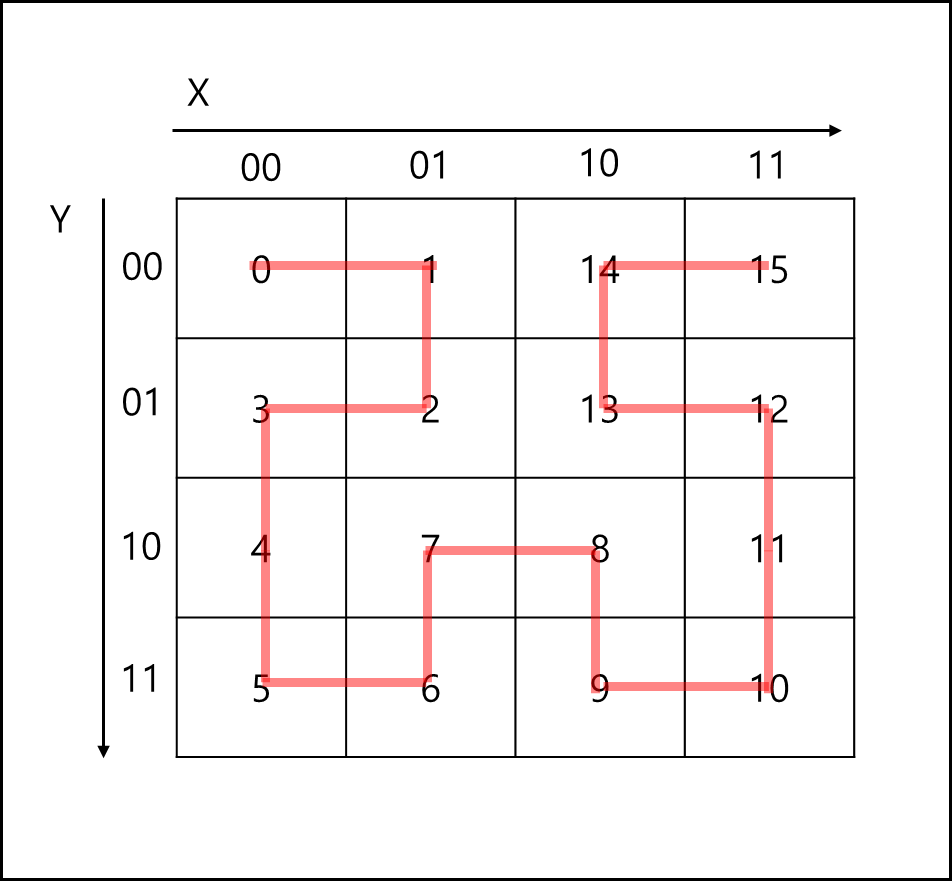
z-order를 만드는 방식은 아래와 같다. 어떤 평면을 X와 Y로 4개씩 나누어 총 16칸을 만들었다고 해보자.
총 인덱스로 만들면 X와 Y 각각 0~3까지이다.
이를 비트로 만들면 2비트로 표현이 가능하며 X축의 각각 비트를 X_1, X_2라고 Y축 각각 비트를 Y_1, Y_2라고 하자.
각각 칸에 INDEX를 부여할때 X_1 Y_1 X_2 Y_2 순으로 비트를 붙여서 INDEX를 만든다.
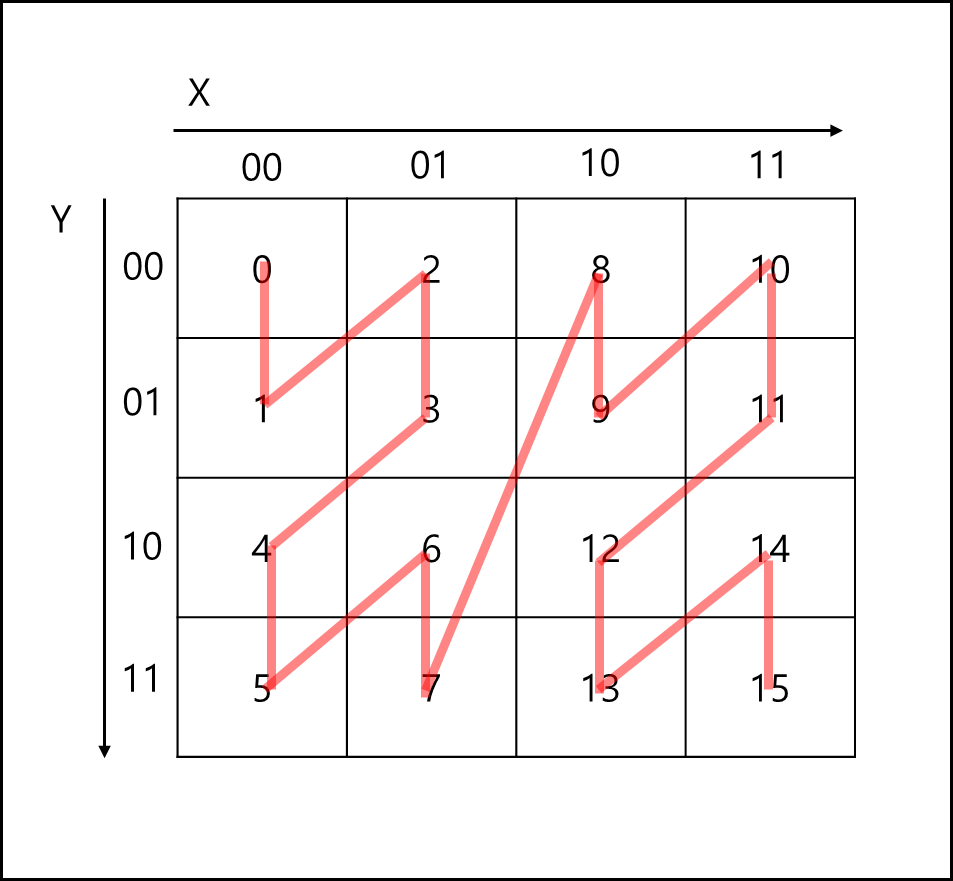
이를 그림을 나타내면 아래와 같다.
비트로 표현한 값을 10진수로 표현하면 아래와 같이 Z-Order가 나타난다.
- Hilbert curve
앞서 말했듯이 Z-order의 경우에는 2차원에서 원래 데이터가 가깝다고 1차원 인덱스까지 가깝진 않다.
하지만 지금 이야기하는 Hilbert curve의 경우에는 Z-order 보다는 인덱스가 가까울 수록 실제 사분면 간에도 좀 더 가까워서(지역성이 좋다고 말한다)
효율적이다.
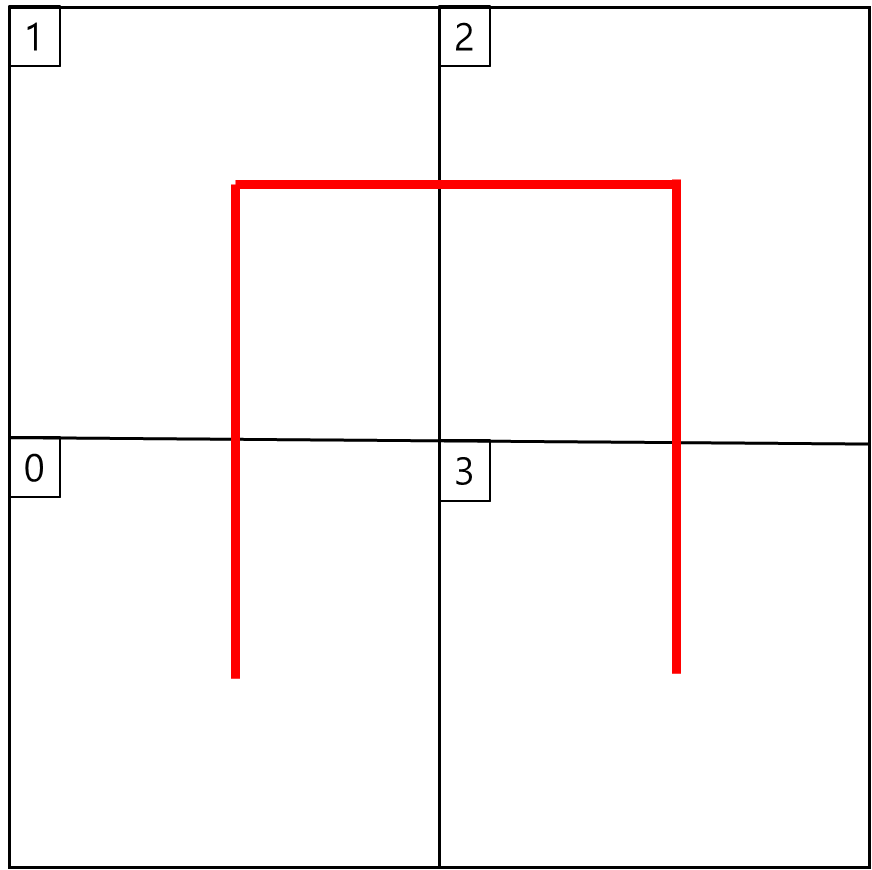
기본적으로 2차원 평면이 있을 때 이를 4분할한 뒤 순서를 아래와 같이 곡선으로 부여한다.
만약 각 사분면의 데이터가 용량을 초과하여 추가적으로 분할해야할 경우 아래와 같이 순서를 부여한다.
이는 기본적인 U 자형 곡선을 동일한 규칙으로 패턴을 만들어 프랙탈과 같이 배치하는 형태이다.
이러한 Hilbert curve는 2 차원 평면상에서 각 데이터의 근접성을 Z-order에 비해 비교적 잘 보존한다 때문에 범위 질의(특히 작은 지역)의 I/O 감소할 수 있다. 하지만 키 계산이 Z-order보다 복잡(회전/반전 상태 관리 필요)하고 2 차원 공간의 모든 이웃 관계를 완벽히 보존할 수는 없다.
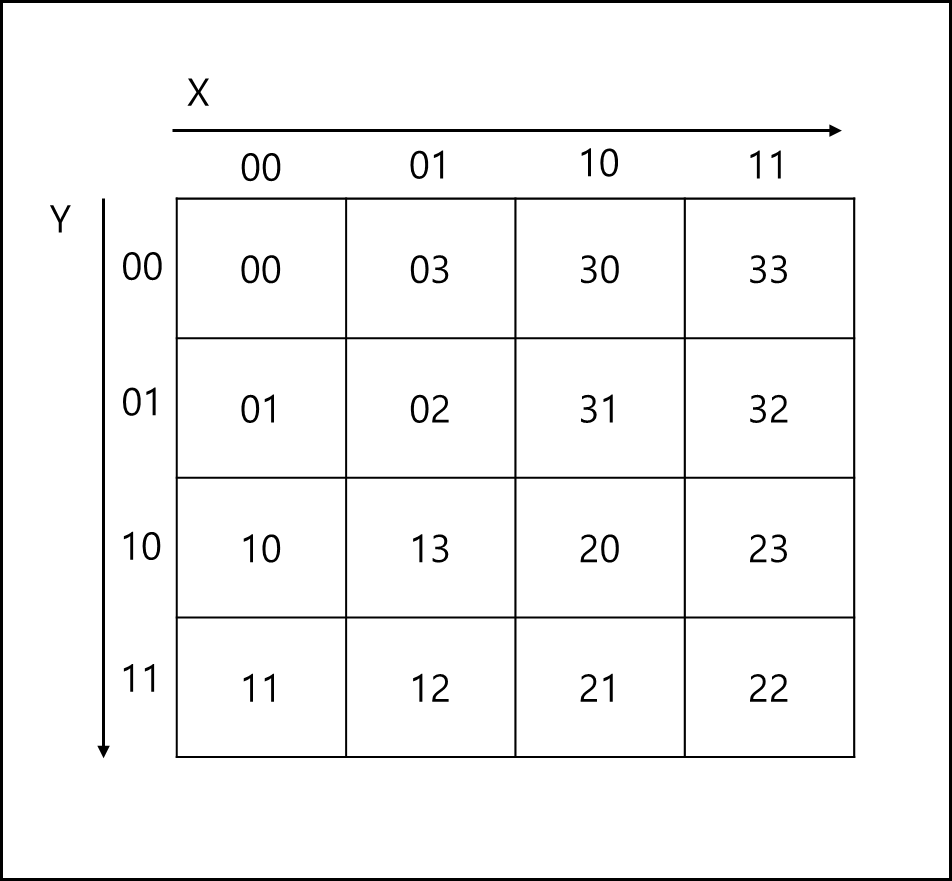
hilbert curve를 만드는 방법은 아래와 같다.
아래와 같이 공간이 나뉘어있다고 해보자.
X와 Y로 나뉘어서 16칸이 있으며 위와 같이 각각의 2bit로 숫자를 매칭해두었다.
위와 같이 매칭해두면 총 4개의 숫자가 되는데, 이를 두개의 숫자대로 뜯어내어 아래와 같이 매칭한다. 00 -> 0, 01 -> 1 , 11 -> 2, 10 -> 3
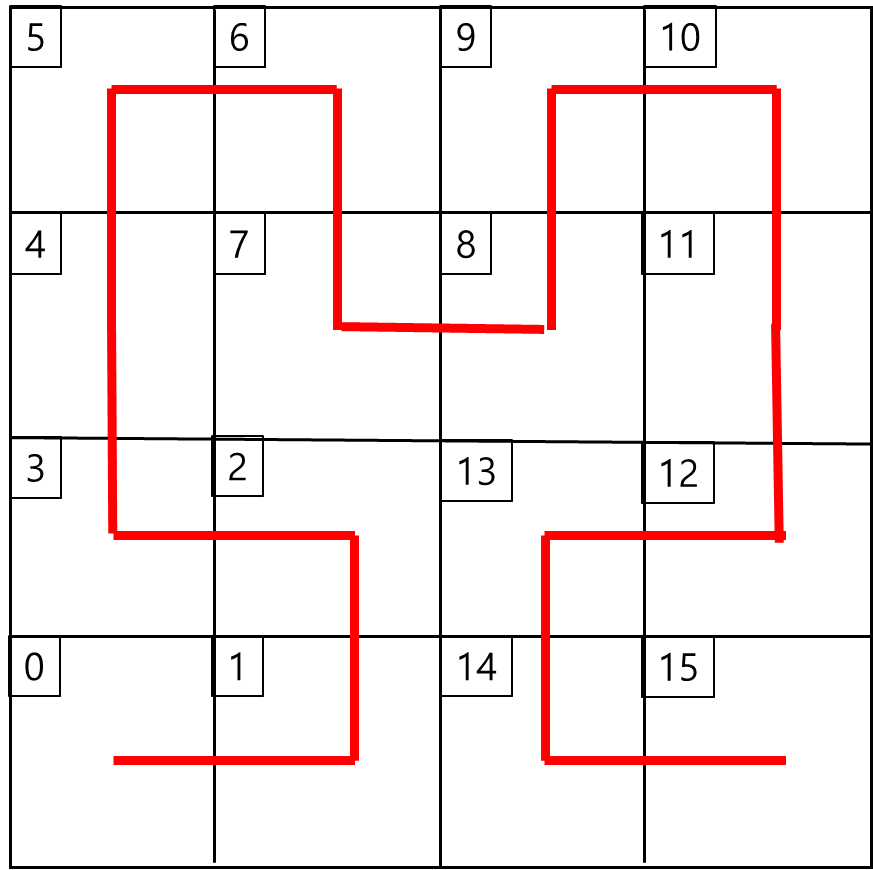
위와 같은 방식대로 바꾸면 아래와 같이 된다.
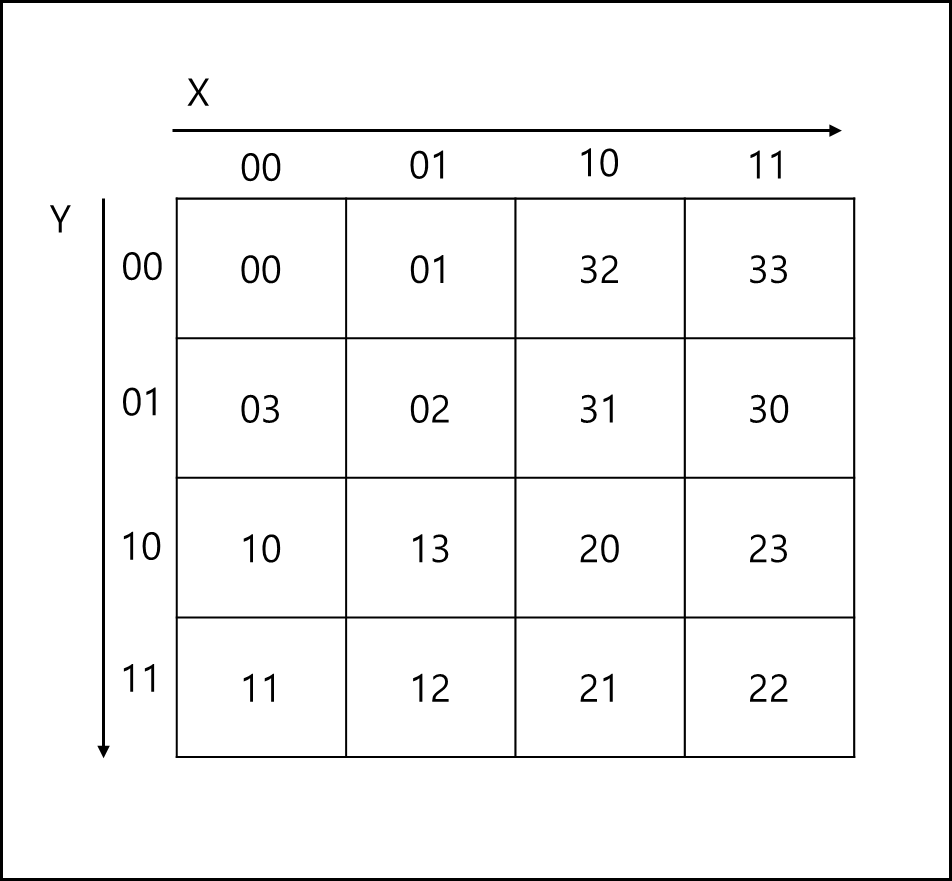
이후 16칸 전체를 돌면서 회전 처리를 해주는데, 앞 숫자가 0,3일때만 처리해준다. 0일때 : 뒤에 나오는 숫자 1과 3을 변경한다. 3일때 : 뒤에 나오는 숫자 0과 2를 변경한다.
이 방식대로 처리해주면 아래와 같이 변경된다.
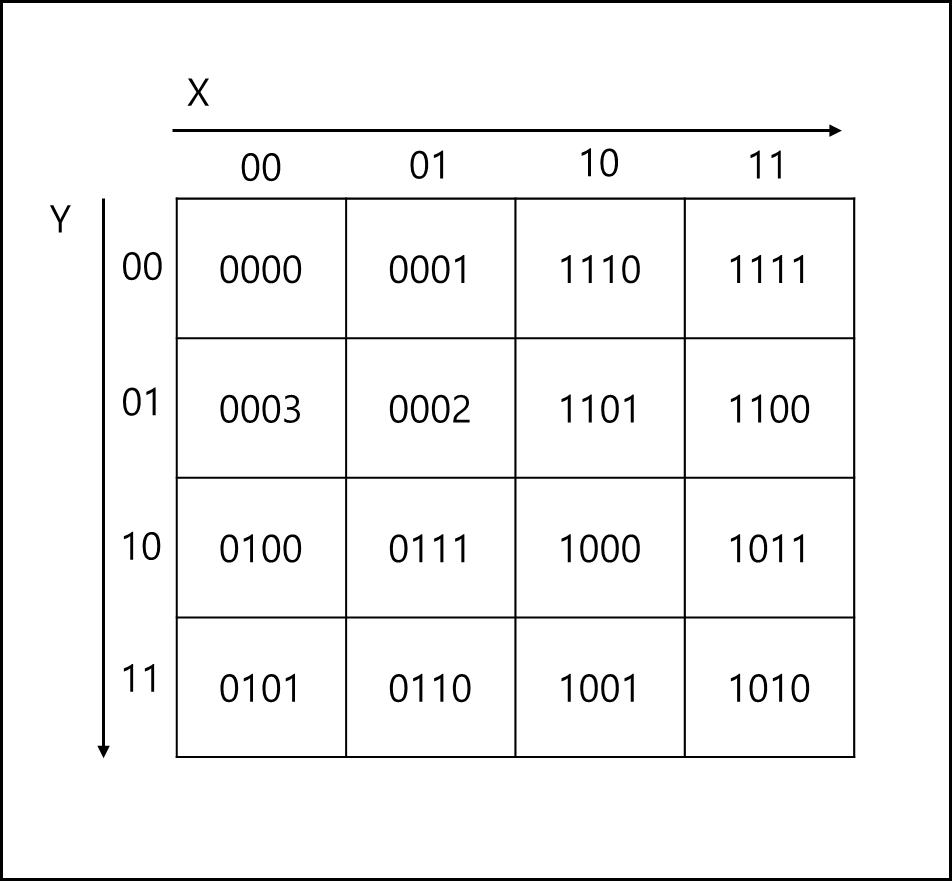
변환된 각 값을 각 숫자마다 다시 2비트 이진으로 표현한다.
4비트를 대상으로 다시 10진수로 변경하면 Hilbert curve를 그리는 순서가 된다.
② 예시
ⓐ 인덱스 빌드
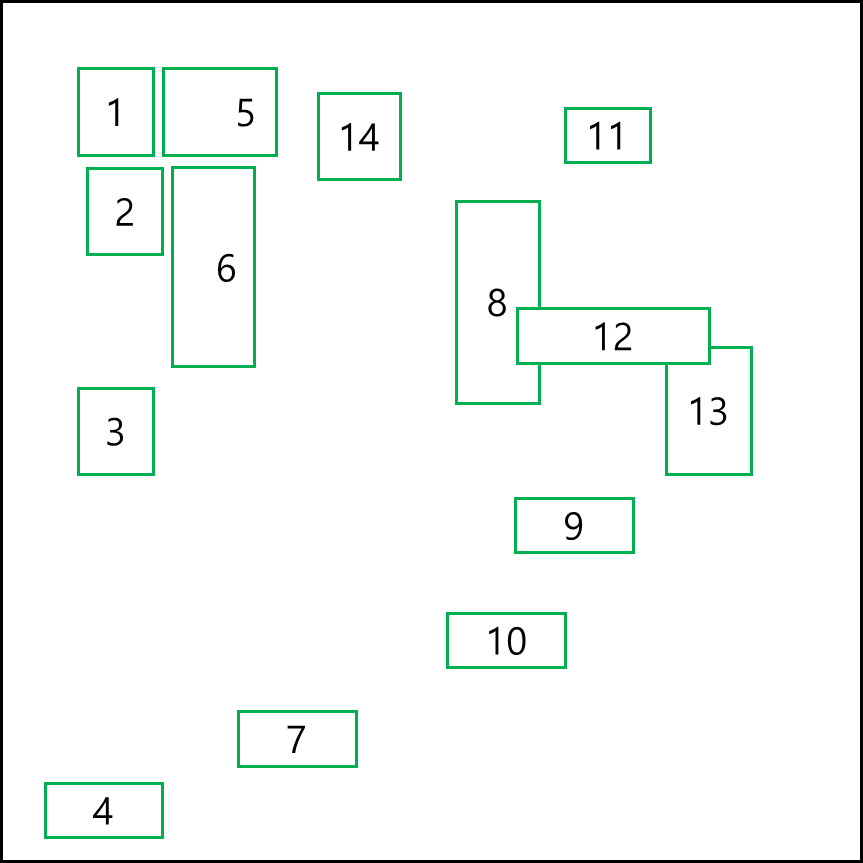
페이지당 4개의 Polygon 정보를 담을 수 있다고 할 때 아래의 그림을 보자. 그림에서 Order는 Z-order로 표현했다.
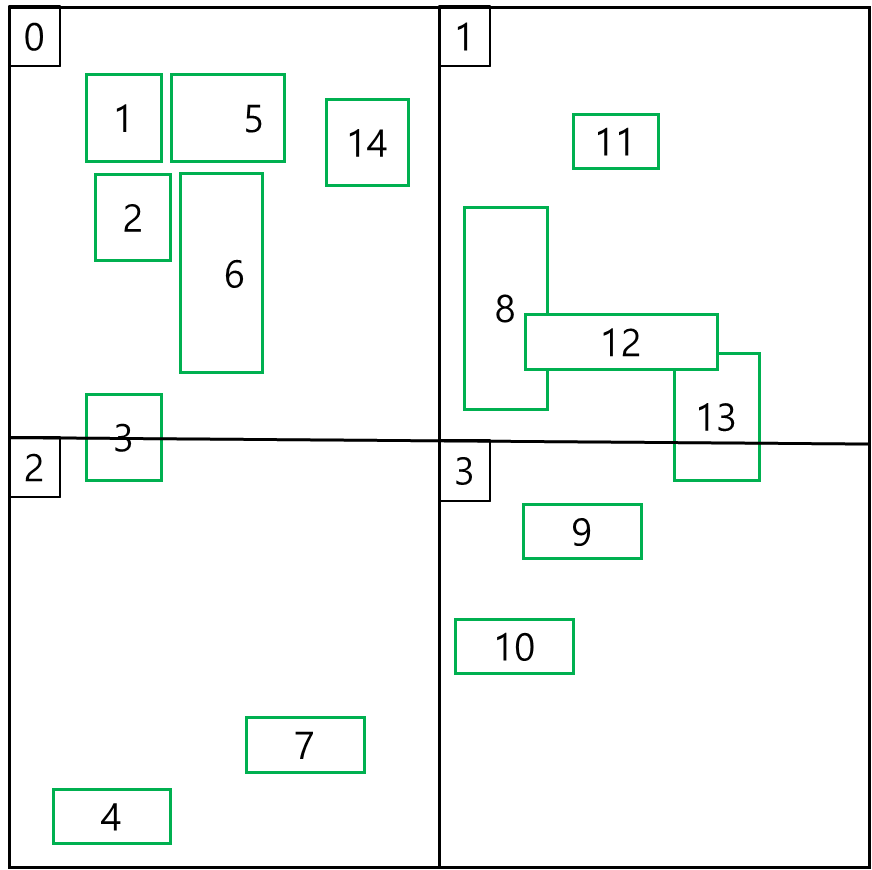
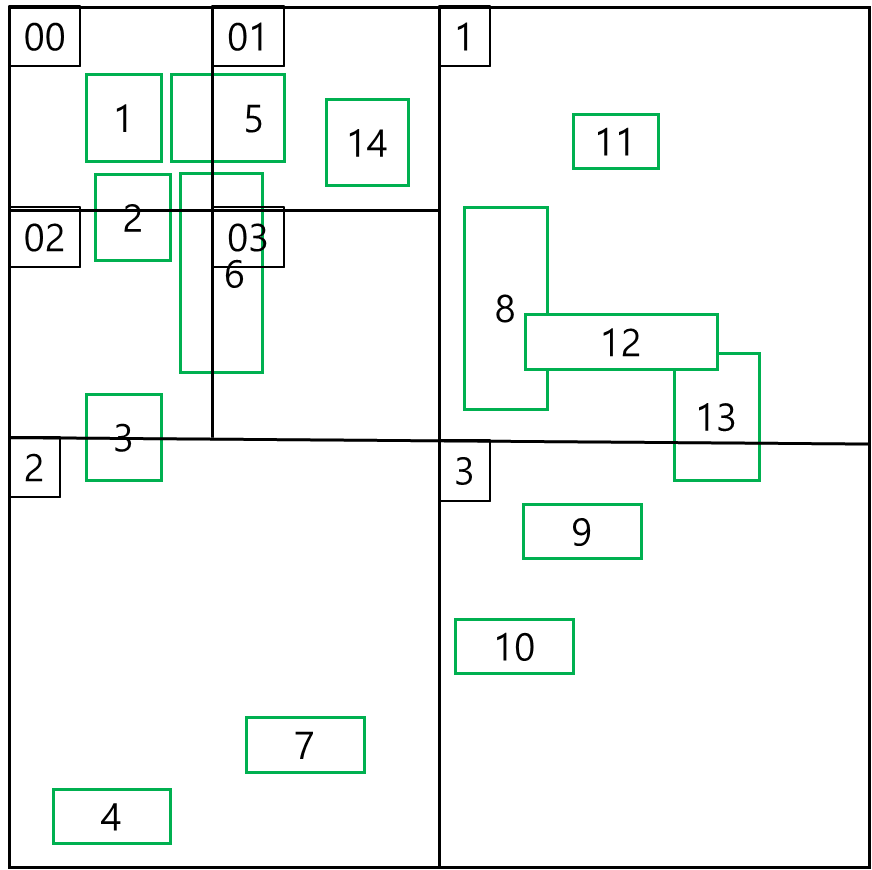
위와 같이 2차원 공간 R에 다음과 같이 다각형의 MBB가 있다. 먼저, R을 4분면으로 나눈다.
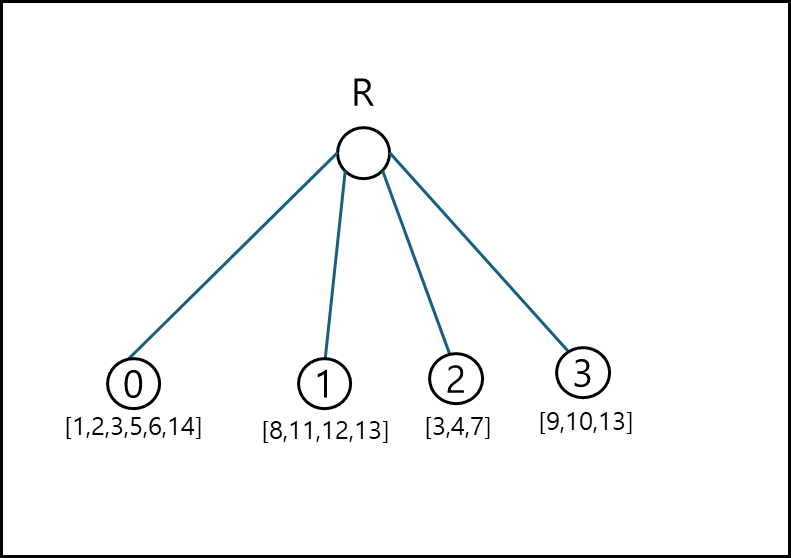
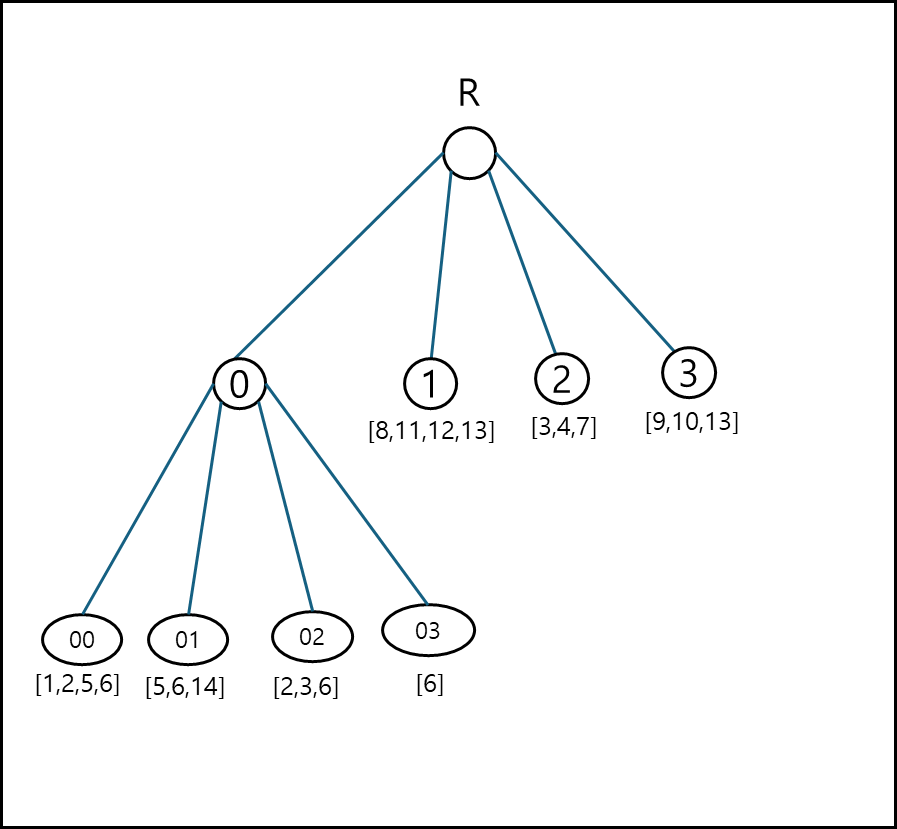
위를 트리로 나타내면 아래와 같다.
각 리프노드는 페이지이다. polygon이 다른 분면에 걸쳐있다면 각 분면에 복제하여 같이 저장한다. 페이지당 4개의 Polygon 정보를 담을 수 있는데, 리프노드 0을 보면 4개가 초과되어있다.
따라서 리프노드 0을 분할하기 위해 공간을 다시 4분면으로 분할 한다.
위와 같이 분할된 값을 다시 트리로 그리면 아래와 같다.
보면 알겠지만 각 분면에 겹치는 mbb가 많을 수록 데이터의 중복이 많은 것을 알 수 있다.
ⓑ 값 추가
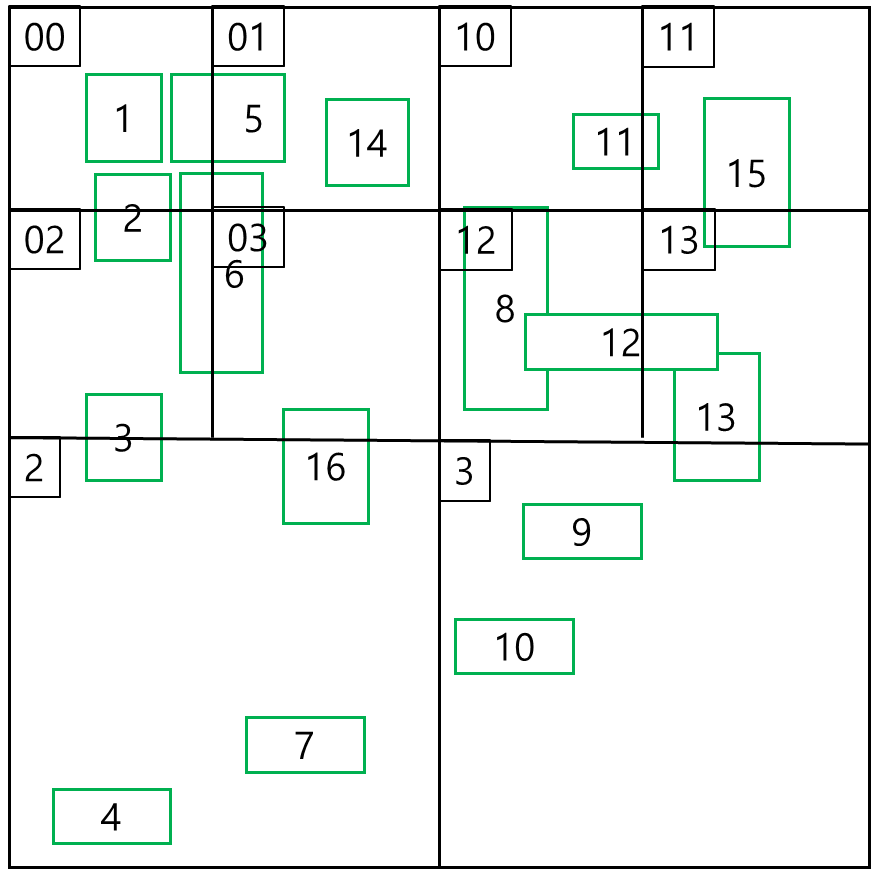
아래는 15와 16가 추가 되는 경우 어떻게 분할되는지를 설명하는 그림이다.
보면 알겠지만 사분면 1과 15가 추가되었고 0,1에 걸쳐 16이 추가된 걸 볼 수 있다.
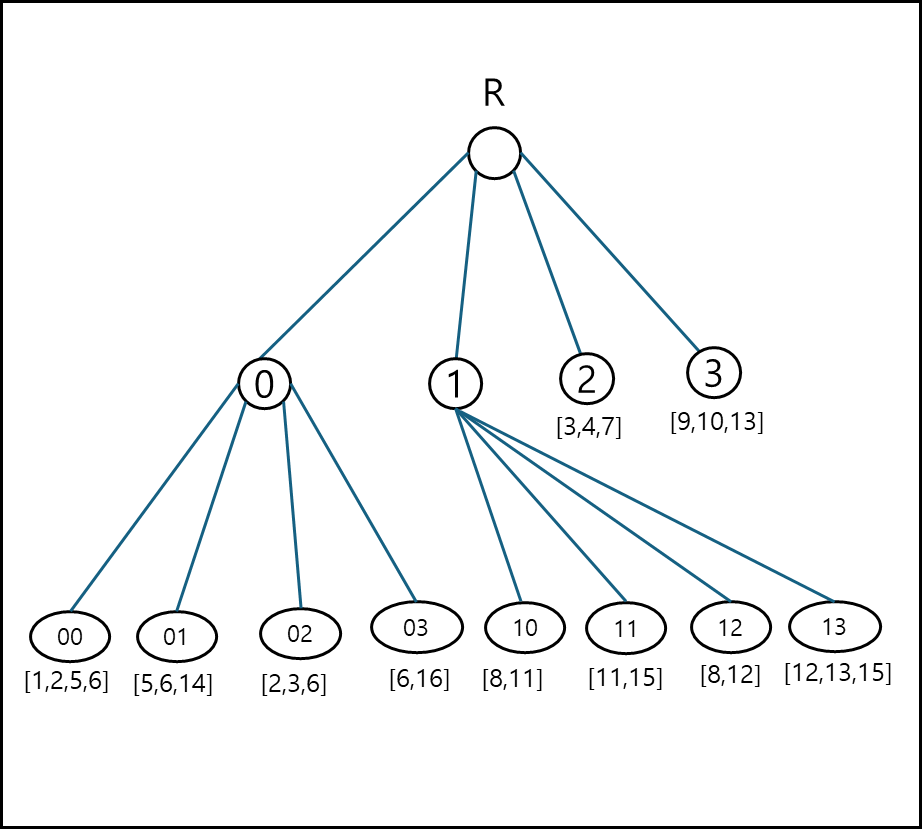
이 경우 사분면 1의 용량이 초과되었음로 4분할 하여 10,11,12,13으로 만든다.
16의 경우 사분면의 용량이 초과하지 않았으므로 분할없이 추가된다.
이를 트리로 나타내면 아래와 같다.
ⓒ 포인트 검색
찾고자 하는 점 P가 있을 때 위 예시에서 검색하는 절차는 아래와 같다.
1
2
3
4
5
6
7
result = ∅
l = POINTLABEL(P) // Step 1: 점 P의 쿼드트리 라벨 계산
[L, p] = MAXINF(l) // Step 2: B+-트리에서 l 이하(또는 최적의 엔트리)를 찾음
page = READPAGE(p) // Step 3: 해당 페이지(디스크/메모리 블록)를 읽음
for each e in page do
if (e.mbb contains P) then result += {e.oid} // MBB(최소경계박스)로 최종 검사
return result
점 P가 어느 쿼드트리 셀안에 있는지 찾아서 반환(l)한다. 가령 마지막 예시에서 00 평면에 있다면 00을 반환하는 식이다.
어느 평면에 있는지 얻었다면(위 예시에선 l값 즉, 00) 이를 이용해서 B+ 트리에서 이 값을 가지고 탐색(MAXINF)하여 관련 페이지 포인터(p)를 얻는다.
해당 페이지 포인터를 읽어서(READPAGE(p)) page 안에 있는 값을 얻는다(1,5,2,6).
얻은 값을 반복문으로 돌려서 해당 MBB안에 P 값이 포함되어있는지 확인하고 반환 집합(result)에 넣는다.
모두 검사했으면 반환 집합을 반환한다.
ⓓ 범위 검색
아래는 어떤 직사각형 W에 걸쳐있는 객체들을 찾는 방법이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
result = ∅
// Step 1: 윈도우의 꼭짓점 라벨 계산
l = POINTLABEL(W.nw)
[L, p] = MAXINF(l)
l' = POINTLABEL(W.se)
[L', p'] = MAXINF(l')
// Step 2: B+-트리에서 키 구간 [L, L']에 해당하는 엔트리 집합 Q 얻기
Q = RANGEQUERY([L, L'])
// Step 3: 각 엔트리 q ∈ Q에 대해
for each q in Q do
if QUADRANT(q.l) overlaps W then // 쿼드셀(그 엔트리가 가리키는 영역)이 윈도우와 겹치면
page = READPAGE(q.p) // 페이지 읽기
for each e in page do
if (e.mbb overlaps W) then result += {e.oid} // MBB(객체 경계)가 W와 겹치면 후보로 추가
end for
end if
end for
// 정렬하고 중복 제거
SORT(result); REMOVE_DUPL(result)
return result
W값의 범위를 나타내는 2개의 점인 NW(왼쪽 위)와 SE(오른쪽 아래) 점의 쿼드 트리의 셀이름(라벨, NW=l, SE=l’)을 찾아서 반환한다.
l ~ l’에 해당하는 Page를 모두 읽어온다.
해당 Page에서 mbb의 값을 모두 갖고 와서 W와 겹치면 result 배열에 넣는다.
result를 정렬하고 중복을 제거한다
result 배열을 반환한다.
③ 단점
위 방식의 단점을 정리하면 아래와 같다.
- 소수의 자식 노드는 페이지의 작은 부분만 차지하는 4개로 고정된다.
- 쿼드트리 쿼리 시간은 트리 깊이와 관련이 있으며, 깊이가 클 수 있기 때문에 쿼리 시간이 길어질 수 있다.
- 페이지에 들어간 polygon의 중복이 매우 많다.
d. The z-ordering tree
이전까지의 방법들은 모두 Polygon들의 mbb 값을 가지고 비교를 했다.
하지만 지금 소개할 방법은 MBB 값이 아닌 실제 polygon 값을 가지고 모델링하는 방식이다.
이전의 linear quadtree는 그때 그때 4개로 분할했던 반면 Z-ordering tree는 전체 2차원 평면을 4의 d승으로 미리 나누어두며, 실제 polygon의 point와 edge가 겹치는 부분을 최대 차수가 4인 B+ 트리의 leaf node에 사분면 이름과 어떤 polygon인지 정보를 가지고 있다.
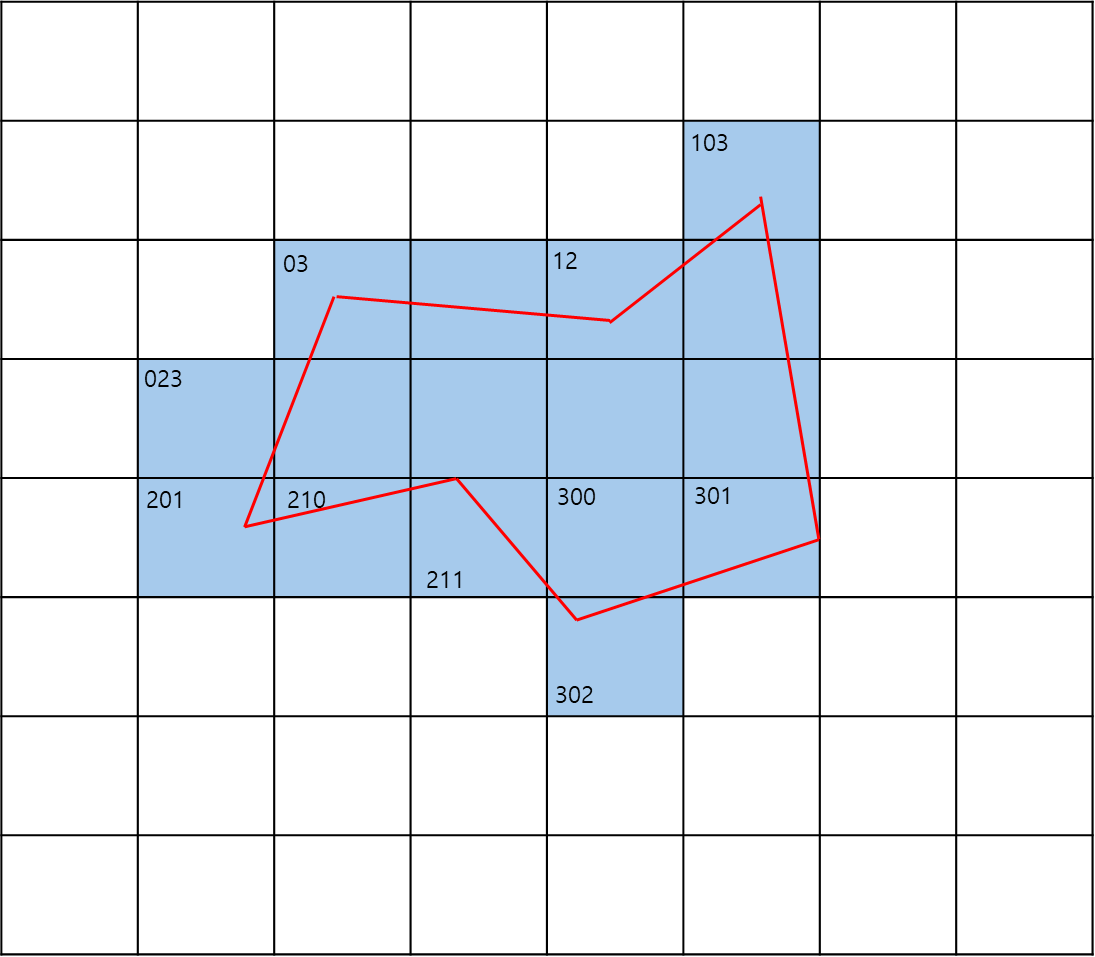
아래의 경우에는 d가 3으로 64개의 사분면으로 나뉜 평면이다.
어떤 polygon a가 위와 같이 해당 사분면에 대해서 overlap되어있다면 overlap된 사분면 번호는 아래와 같다.
{023, 03, 103, 12, 201, 210, 211, 300, 301, 302}
중간 중간 4개씩 겹친건 상위 번호로 퉁칠 수 있다(ex- 030,031,032,033 = 03)
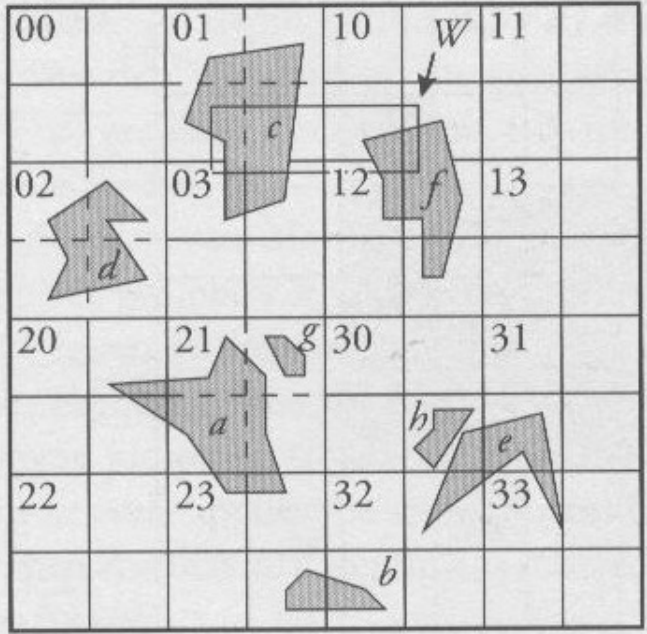
한 개의 polygon은 명료하지 않으니 다수의 polygon으로 설명을 해보겠다.
a~h까지 해당하는 polygon들이 속한 사분면을 적으면 아래와 같다.
a={201,203,21,230,231}
b={233,322}
c={01,030,031}
d={02}
e={303,312,321,330}
f={102,103,120,121,123}
g={211}
h={303}
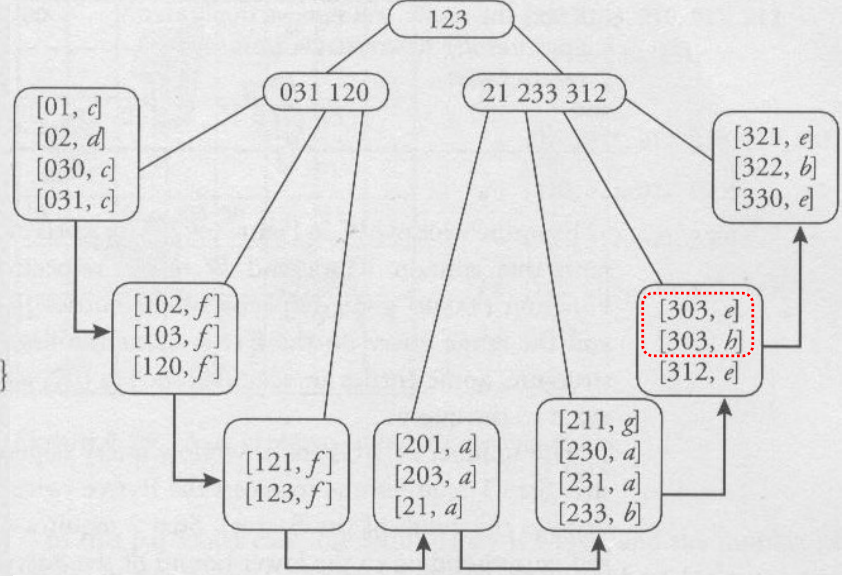
위 정보를 최대 차수가 4인 B+ tree에 넣으면 아래와 같이 표현된다.
위의 (그림 1)에 보면 검색 Window인 W를 볼 수 있는데, 이를 기준으로 검색하는 알고리즘은 아래와 같다.
- result = ∅로 초기화.
- (Step 1) 윈도우 W의 두 꼭짓점 W.nw(왼쪽 위), W.se(오른쪽 아래)를 z-order label로 변환:
l = POINTLABEL(W.nw)
l’ = POINTLABEL(W.se)
(그 옆의 MAXINF 호출은 각 위치에 대응하는 레이블/접두사 형태의 범위 경계를 계산하는 보조 연산이다 — 즉, Z-order상에서 이 점을 포함하는 레이블 구간의 경계값을 얻는다.) - (Step 2) 위에서 얻은 두 경계 L과 L’으로 B+트리에 한 번의 범위 질의(range query)를 날려서, 키 l이 [L, L’]에 속하는 모든 엔트리 E = { [l, oid] } 를 가져온다. 여기서 각 엔트리의 l은 어떤 쿼드트리/사분구역(또는 그 노드의 Morton 레이블)을 가리키고, oid는 그 사분구역에 저장된 객체 식별자이다.
- (Step 3) 얻은 후보들 E를 하나씩 검사:
각 엔트리 e가 가리키는 사분구역(QUADRANT(e.l))이 실제로 윈도우 W와 겹치는지(geometric overlap) 테스트한다.
겹치면 e.oid를 결과 집합에 추가. - 결과를 정렬하고(SORT(result)) 중복(REMOVE_DUPL)을 제거한 뒤 반환한다
e. kd-trees
2차원 평면에서 kd-tree를 생성할때 총 세가지 방법이 있다. 첫번째부터 천천히 알아보자.
ⓐ 첫번째 방법
- x나 y축을 정한다.
- 해당 축에서 가장 중앙값을 가진 값을 찾아 해당 값을 기준으로 절반으로 나눈다.
- 반복하여 x나 y축의 중앙값을 찾아 절반으로 나눈다.
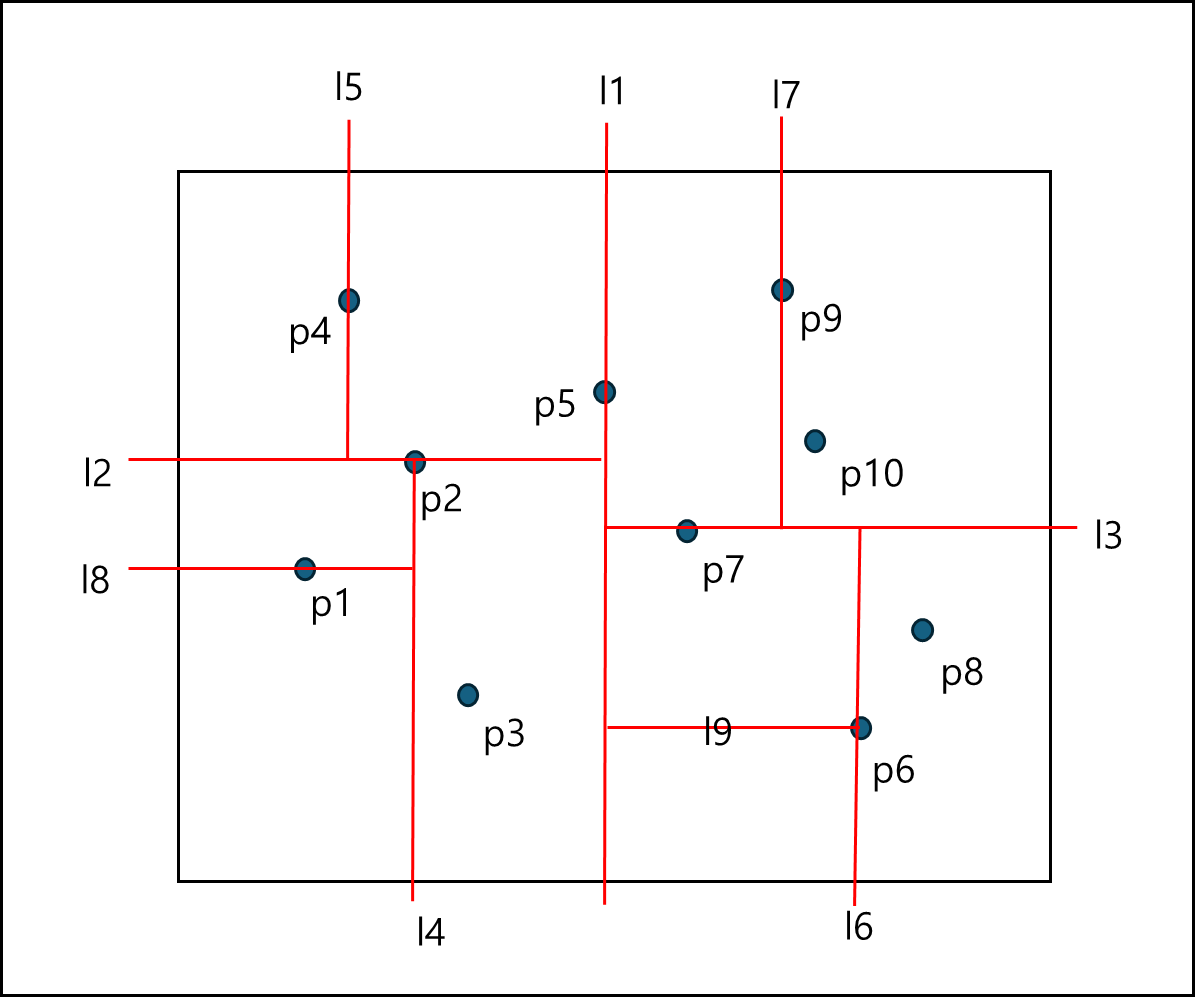
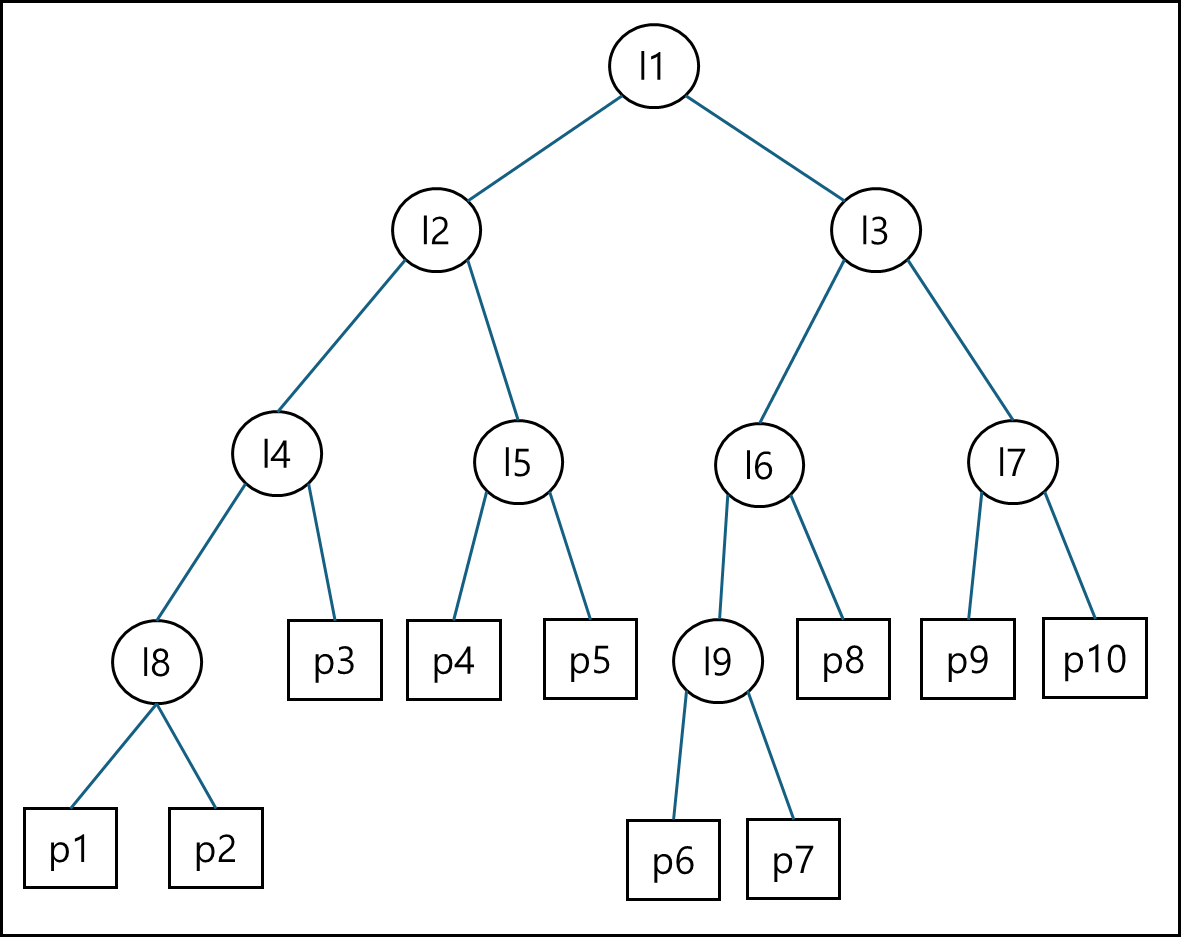
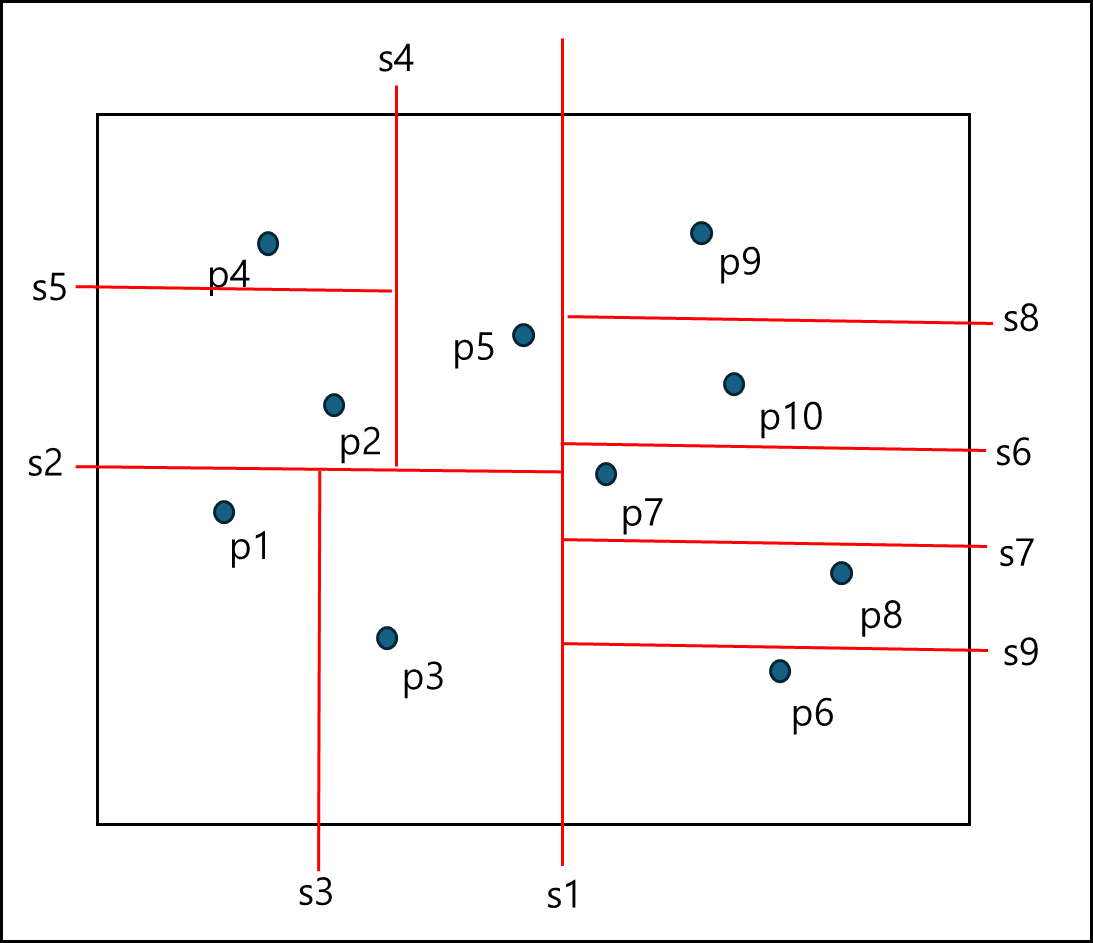
아래의 예시를 보자.
l 번호 순서대로 나뉘는 것이다. 트리로 나타내면 아래와 같다.
ⓑ 두번째 방법
첫번째 방법에서는 중간 값을 가진 Node로 나누었다면 두번째 방법은 Node가 기준이 아니라 별도의 축을 생성하는 것이다. x축이든 y축이든 가장 넓게 퍼져있는 축을 먼저 자르고 각각 중간 값을 자른다. 그림으로 나타내면 아래와 같다.
이를 트리로 나타내면 아래와 같다.
ⓒ 세번째 방법
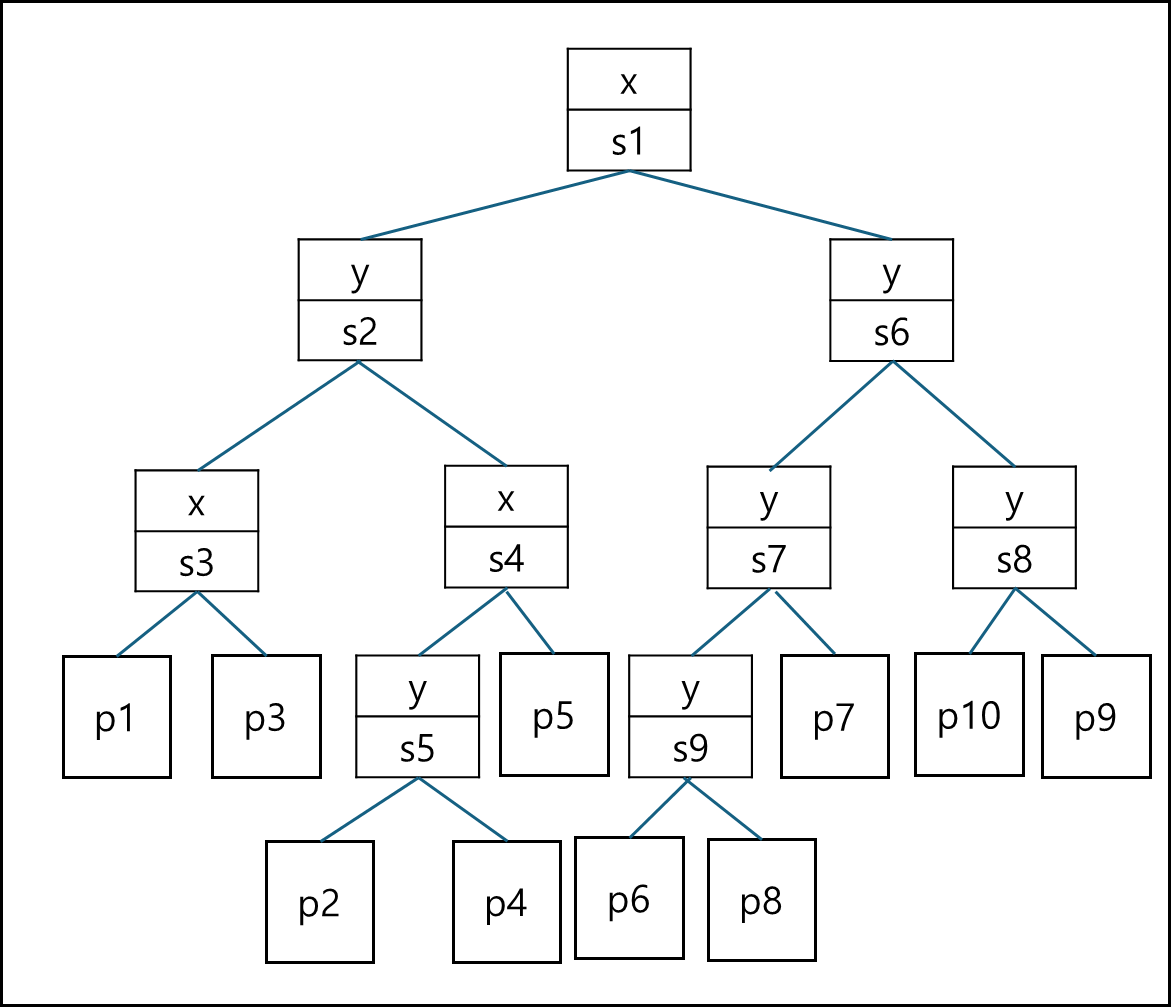
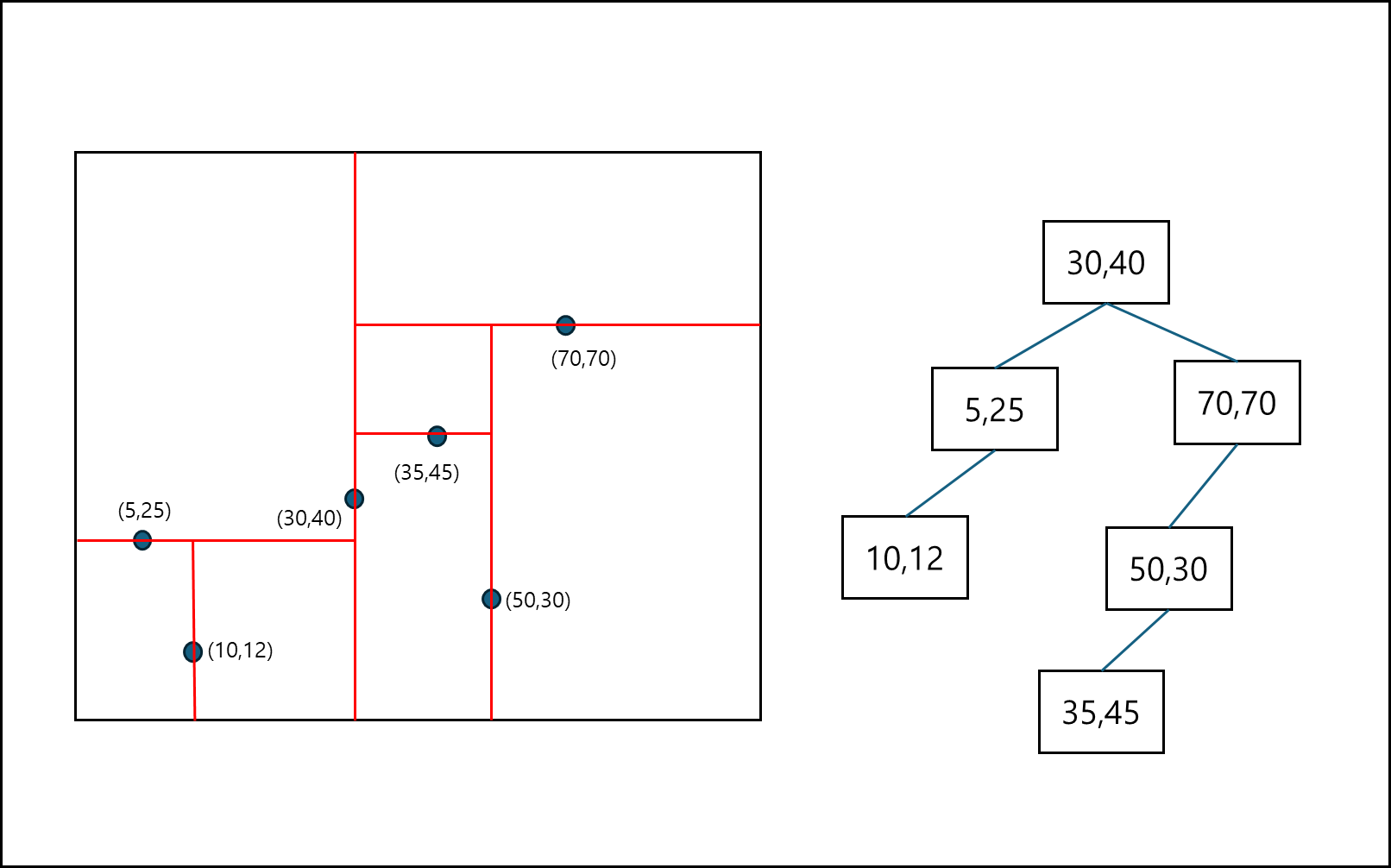
위의 방식들은 Node로 나누느냐 중간 축을 정해서 나누느냐였는데 이번에는 Node로 나누되 x축과 y축을 번갈아가면서 나누는 것이다. Node의 x 축 값만 확인하여 중간값을 선정하여 나누고, y축만 확인하여 중간값을 선정하여 나누는 식으로 재귀적으로 나누어서 트리로 형성하는 방식이다.
아래는 그림과 트리 예시이다.
2) Data-Driven Structure
a. R-tree
위에서 설명했던 방식의 경우에는 데이터가 위치하는 전체 배경을 나누어서 인덱싱한 반면, Data-driven structure 타입인 R-tree는 데이터를 기준으로 기준 MBB를 설정하여 해당 MBB를 기준으로 인덱싱하는 것이다. 이러한 R-tree는 Oracle에서 공간 데이터를 다룰때 기본적으로 제공하는 방식이다. 트리 구조로 되어있으며 각 노드는 최소값 m 이상 최대값 M 이하의 엔트리(Polygon 혹은 인덱스 MBB) 개수를 가진다.
메인 아이디어는 다음과 같은데, 인덱스에 해당하는 부분은 MBB로 지정하여 구성한다(MBB로 나누는 방식은 추후 서술). 전체 공간을 나누어서 저장하기 않기 때문에 각 인덱스와 연결된 페이지는 50% 이상의 활용률을 보장하고 삽입이나 분할 알고리즘 역시 쉽다.
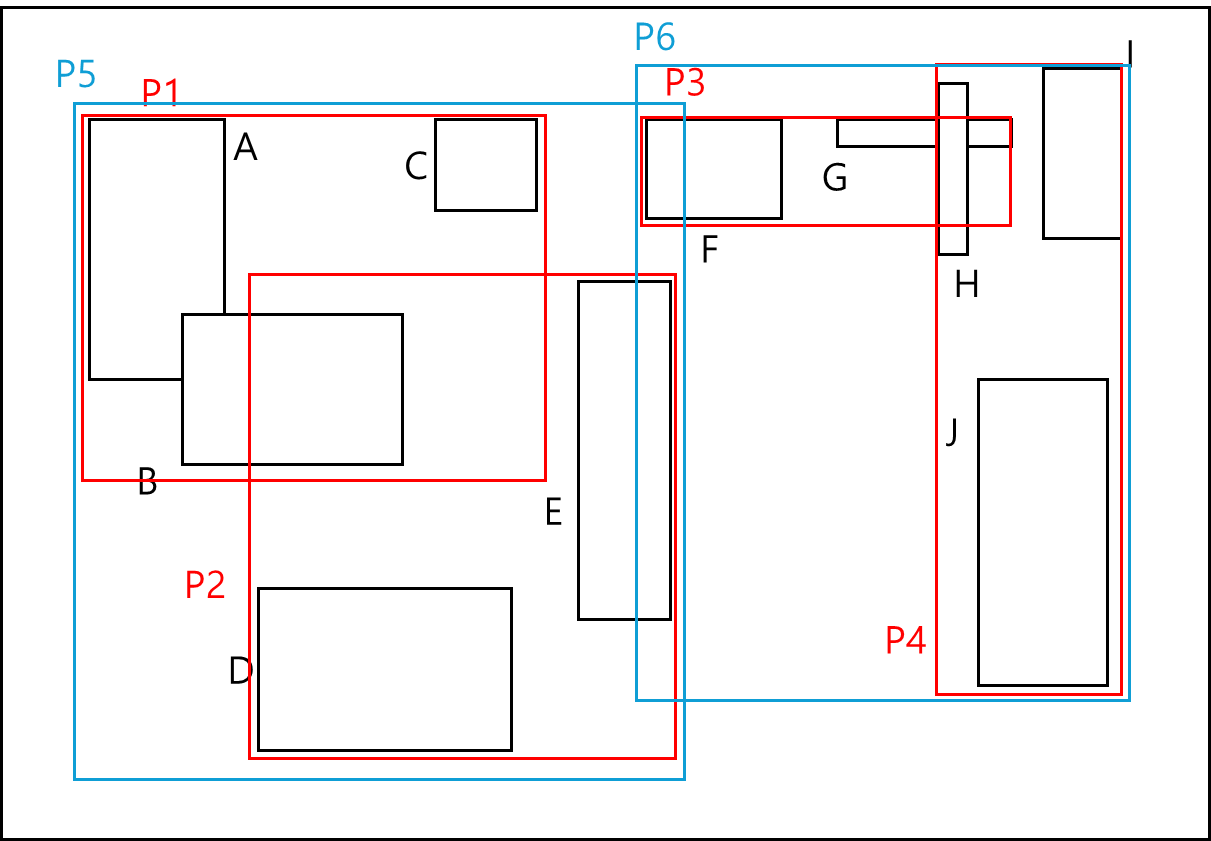
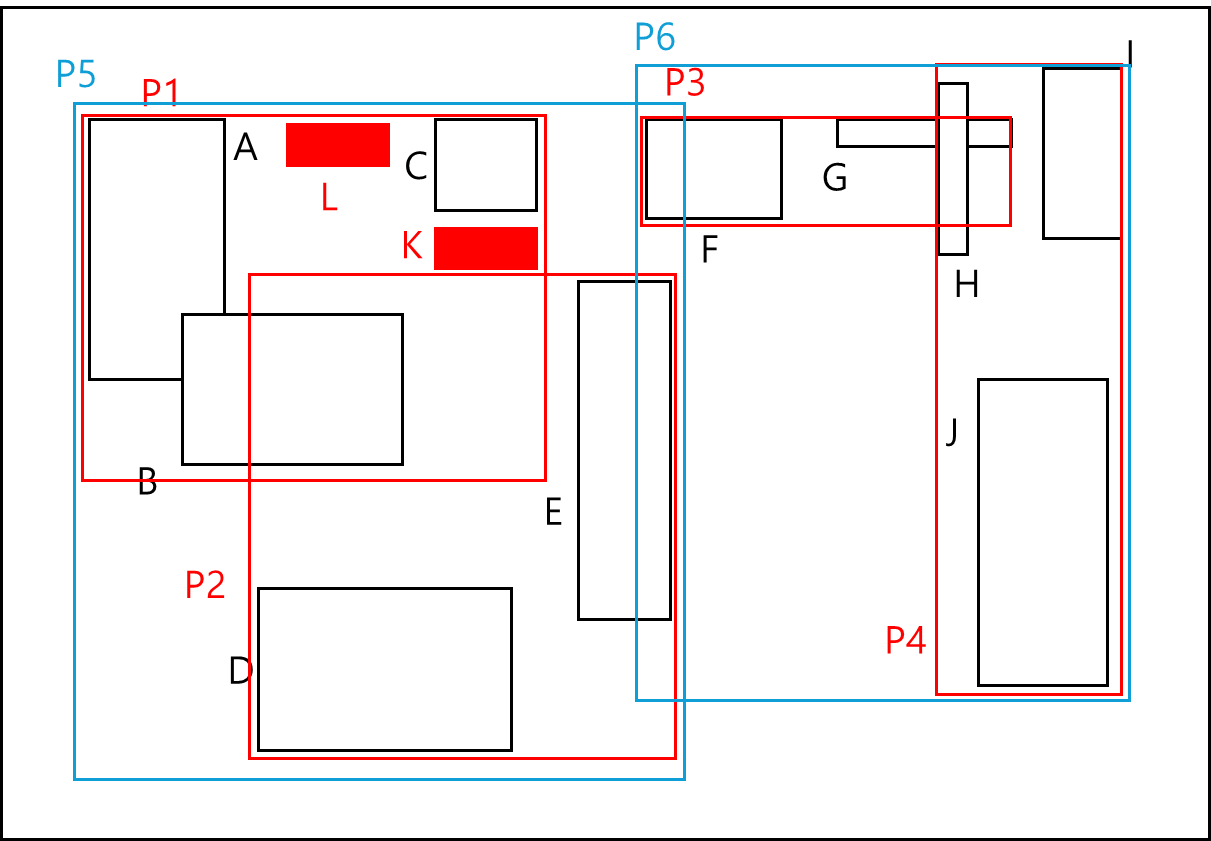
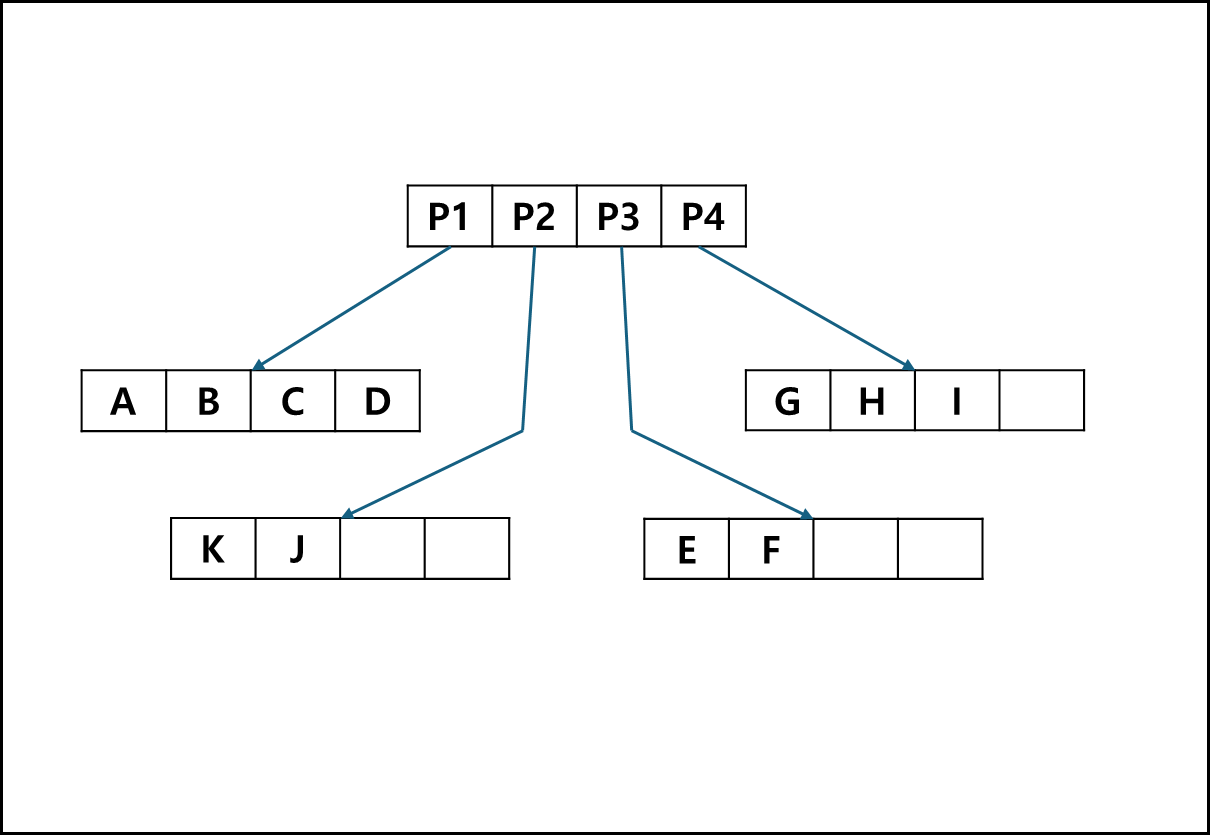
아래의 그림을 보자. polygon A~J의 MBB이다.
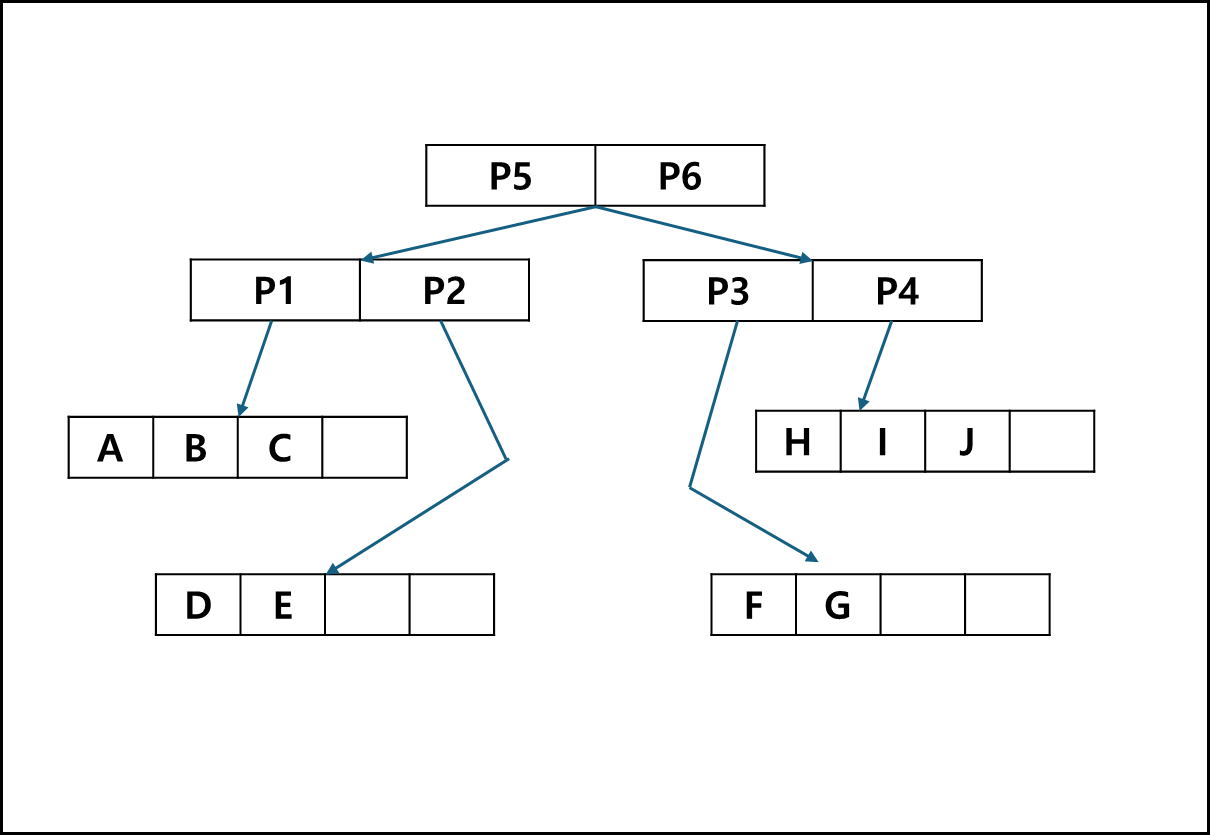
인덱싱간에 왼쪽 위부터 아래로 가면서 Polygon들을 묶고 묶은 크기만큼 mbb로 잡는다. p1은 A,B,C를 묶은 MBB p2는 D,E를 묶은 MBB, p3는 F,G,H를 묶은 MBB, P4는 H,I,J를 묶은 MBB이고, 이들 4개를 2개씩 나누어 MBB를 잡아 P5, P6로 묶는다. 위 그림을 트리로 나타내면 아래와 같다.
각 리프노드는 각각의 Object에 대한 mbb로 이루어져있으며 x에 대해 low,high 값과, y값에 대한 low, high 값을 가지고 있다.
리프노드의 상위 노드들 역시 mbb로 이루어져있기 때문에 x에 대해 low,high 값과, y값에 대한 low, high 값을 가지고 있다.
ⓐ Search
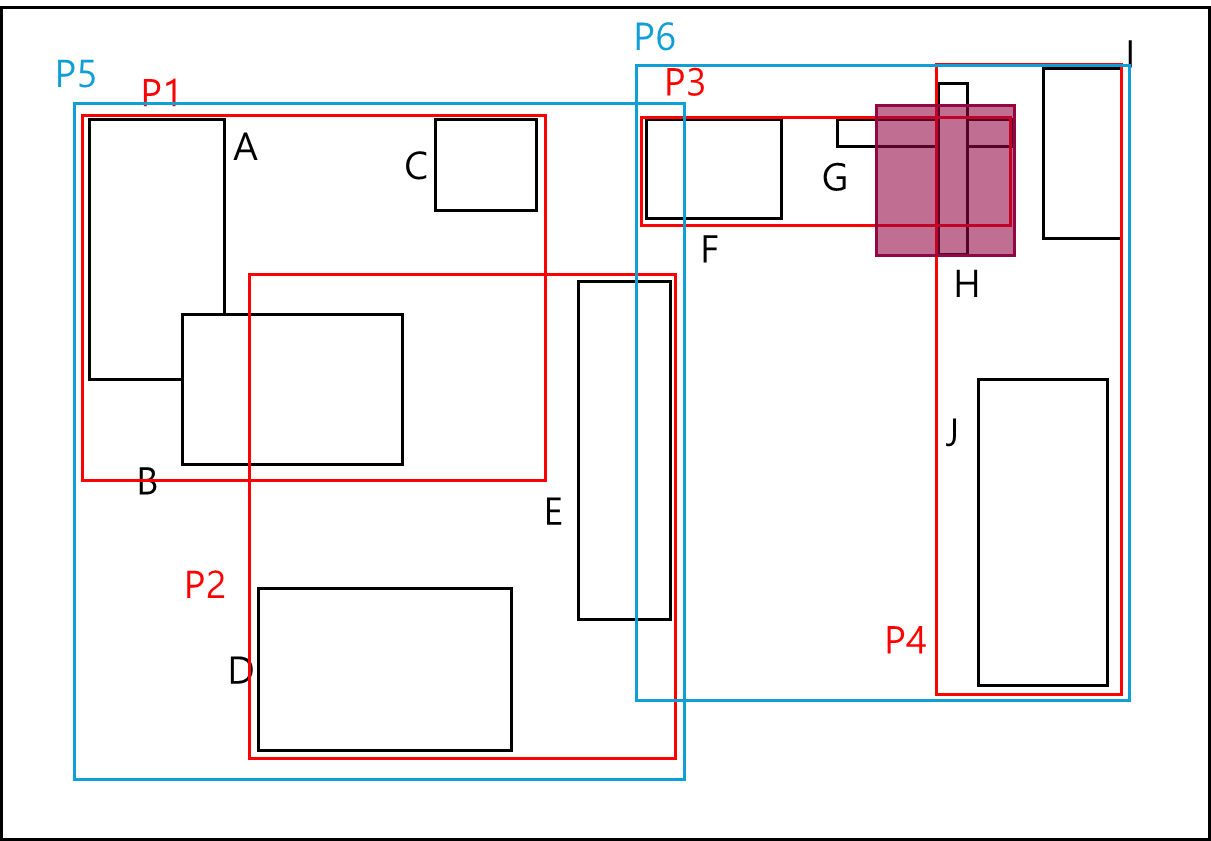
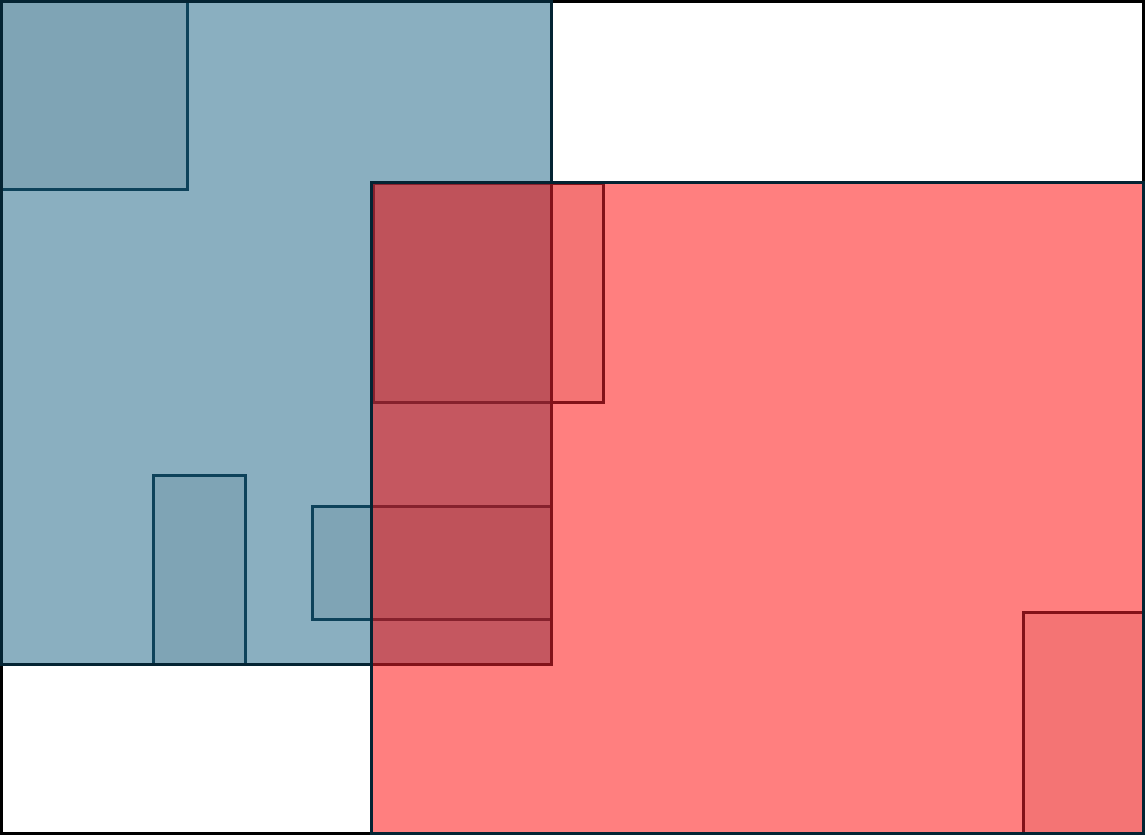
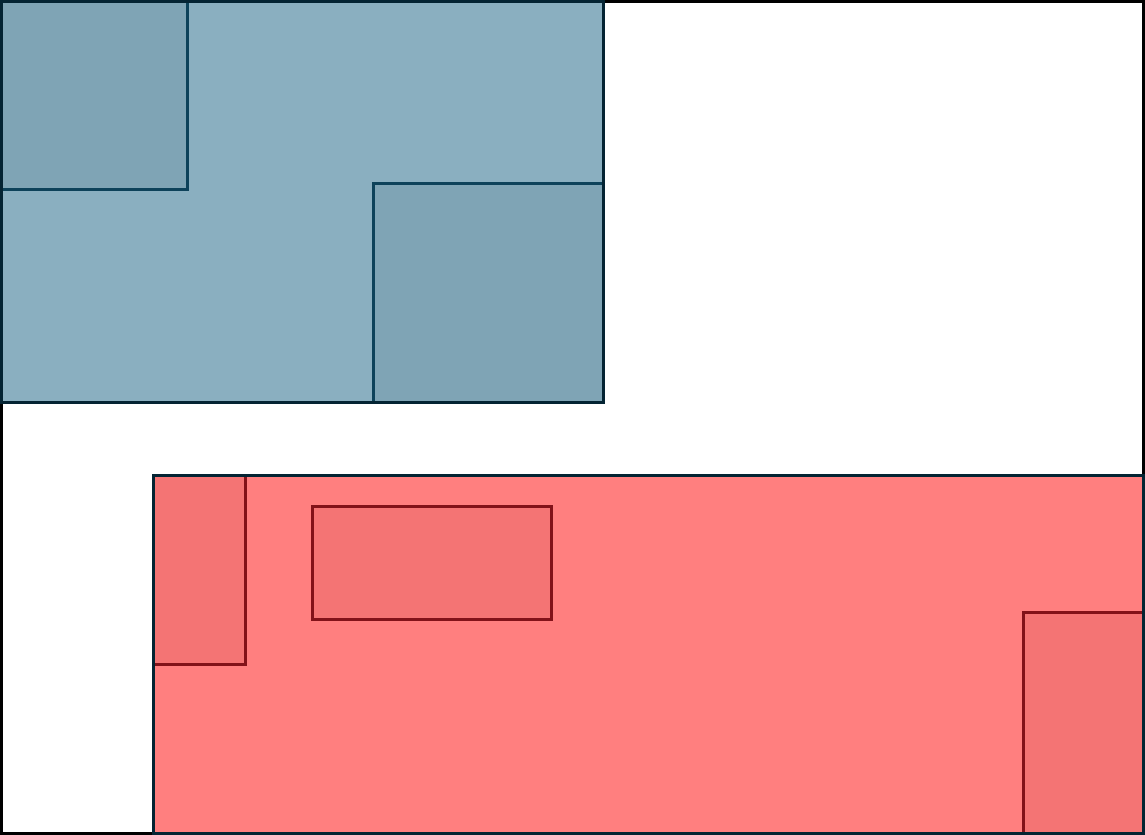
빌드한 index에서 아래와 같이 투명 빨간 사각형 범위에 overlap 되는 mbb에 대한 search를 한다고 해보자.
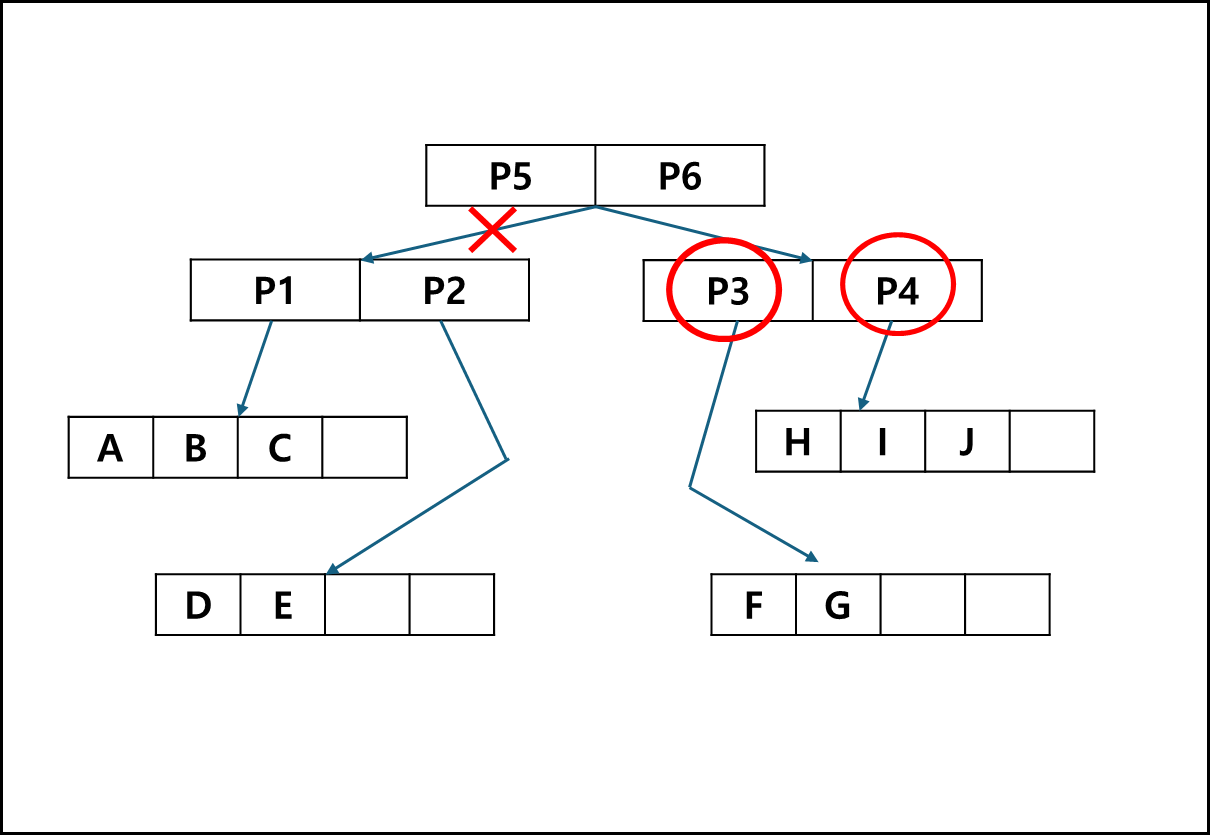
위 그림에서 탐색의 경로는 아래와 같다.
기본적으로 p5와 overlap되지 않으니 해당 경로는 탐색에서 배제된다. 따라서 P6를 따라 내려가게되고, P3와 P4와 겹치는지 확인하게 되는데, 두 MBB와 겹치기 때문에 모든 경로를 확인해야한다.
따라서 H,I,J,F,G를 모두 확인하게 되고 각각의 MBB와 overlap을 확인하여 최종적으로 G,H를 반환한다.
(물론 MBB에 대한 연산이니 이후에 실제 overlap하는지에 대한 검증은 거칠 것이다)
ⓑ Insertion
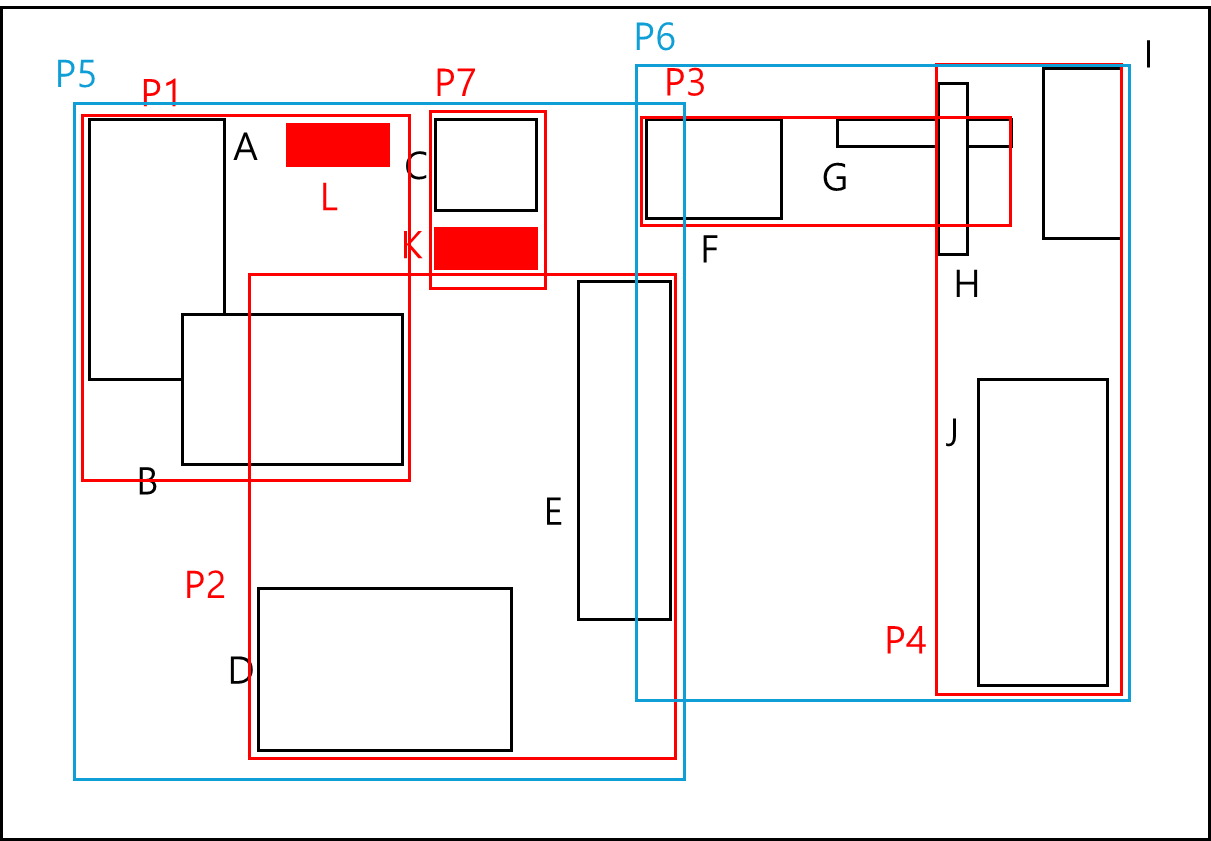
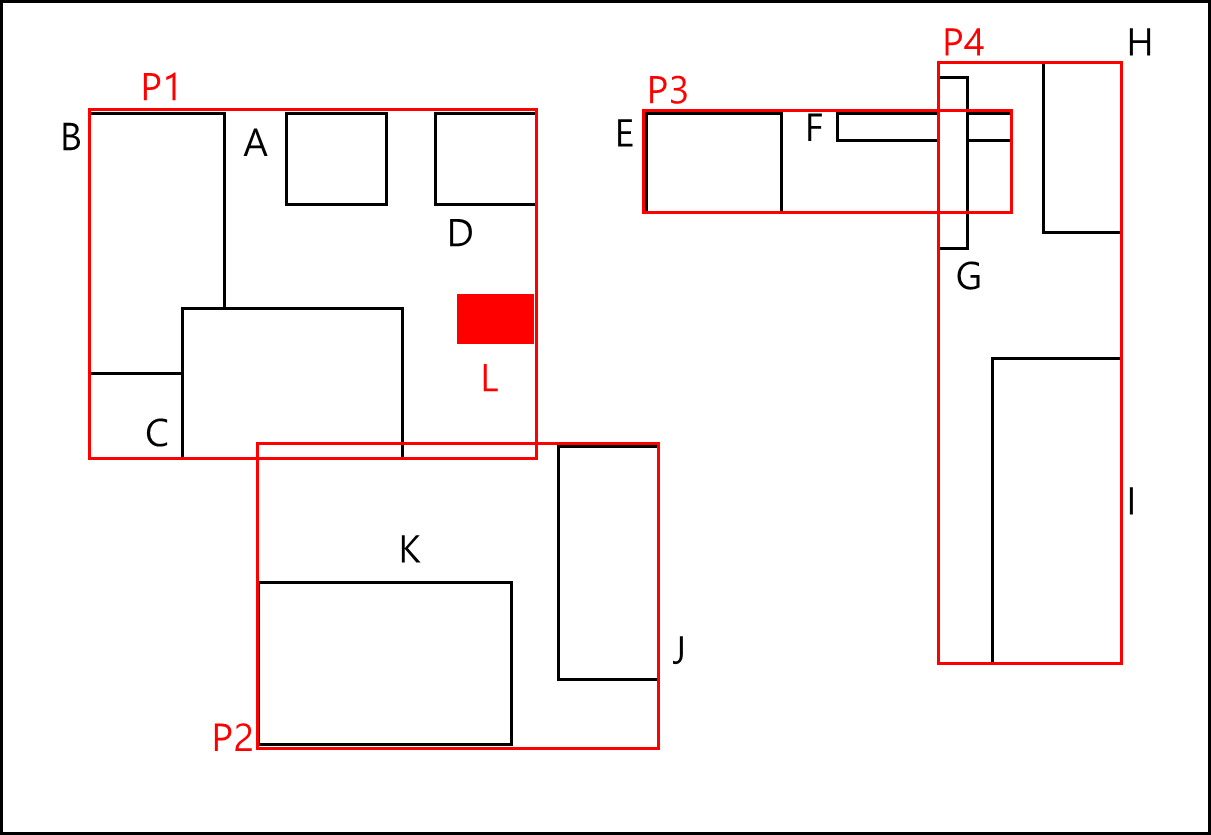
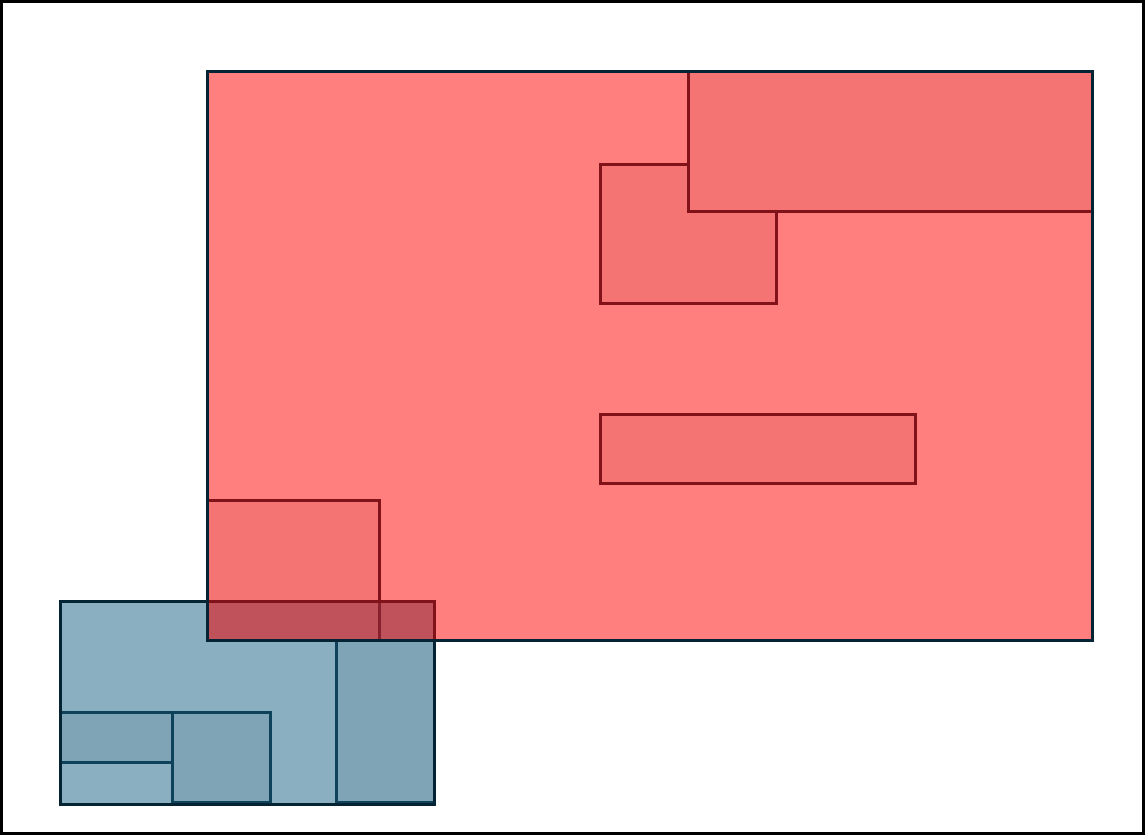
원래 Index에서 아래와 같이 K와 L이 추가되었다고 해보자.
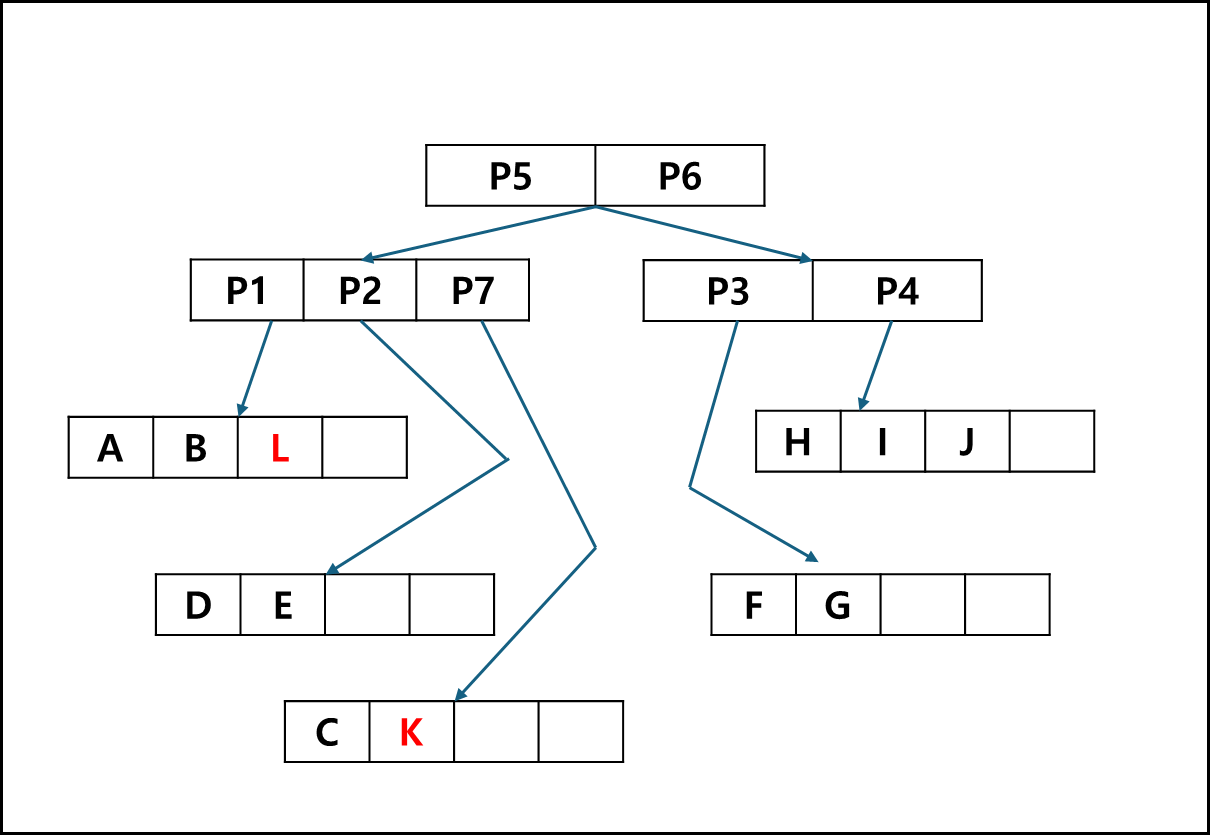
한 노드당 4개씩 담을 수 있으니 분할이 필요하다. 따라서 아래와 같이 분할 할 수 있다.
위와 같이 분할 됨에 따라 트리 역시 아래와 같이 변경 된다.
만약, 상위 트리 노드에서 개수가 4개를 초과한다면 분할하여 상위 노드가 하나 더 생긴다.
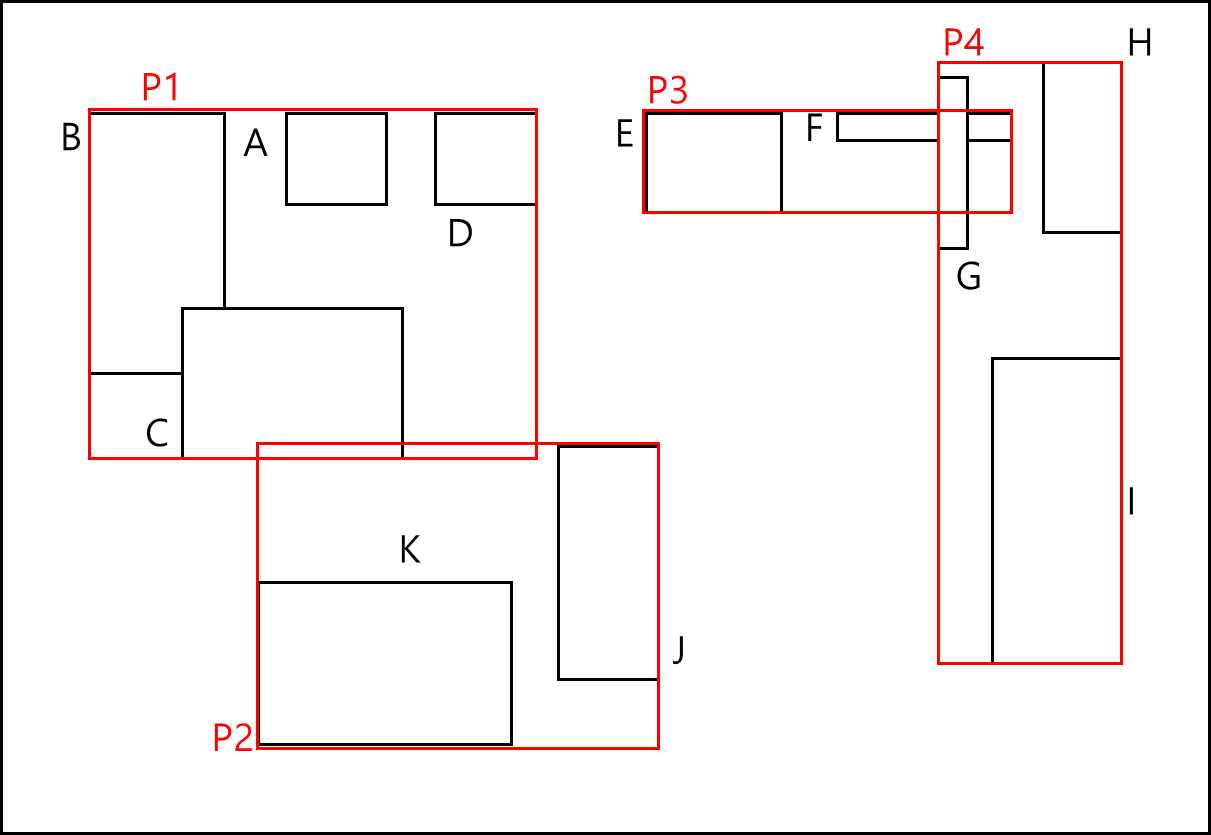
아래의 예시를 보자.
위와 같은 그림에서는 아래와 같은 TREE가 나온다.
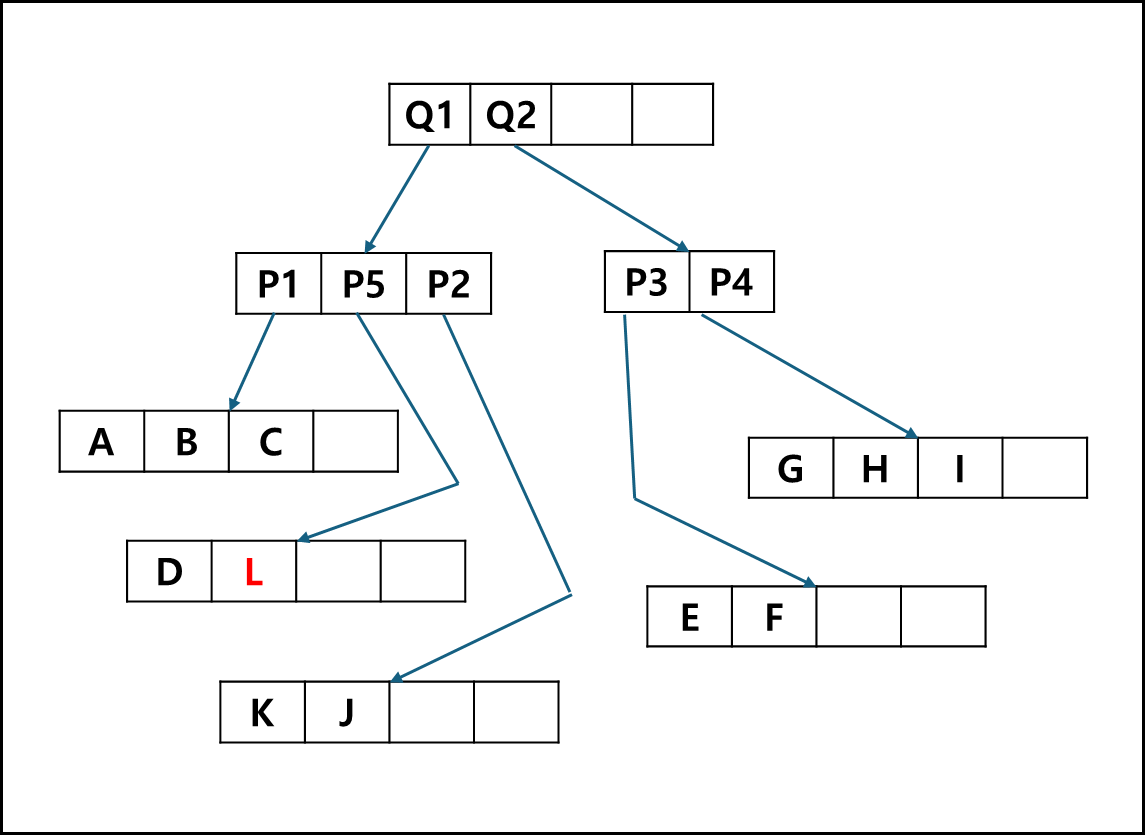
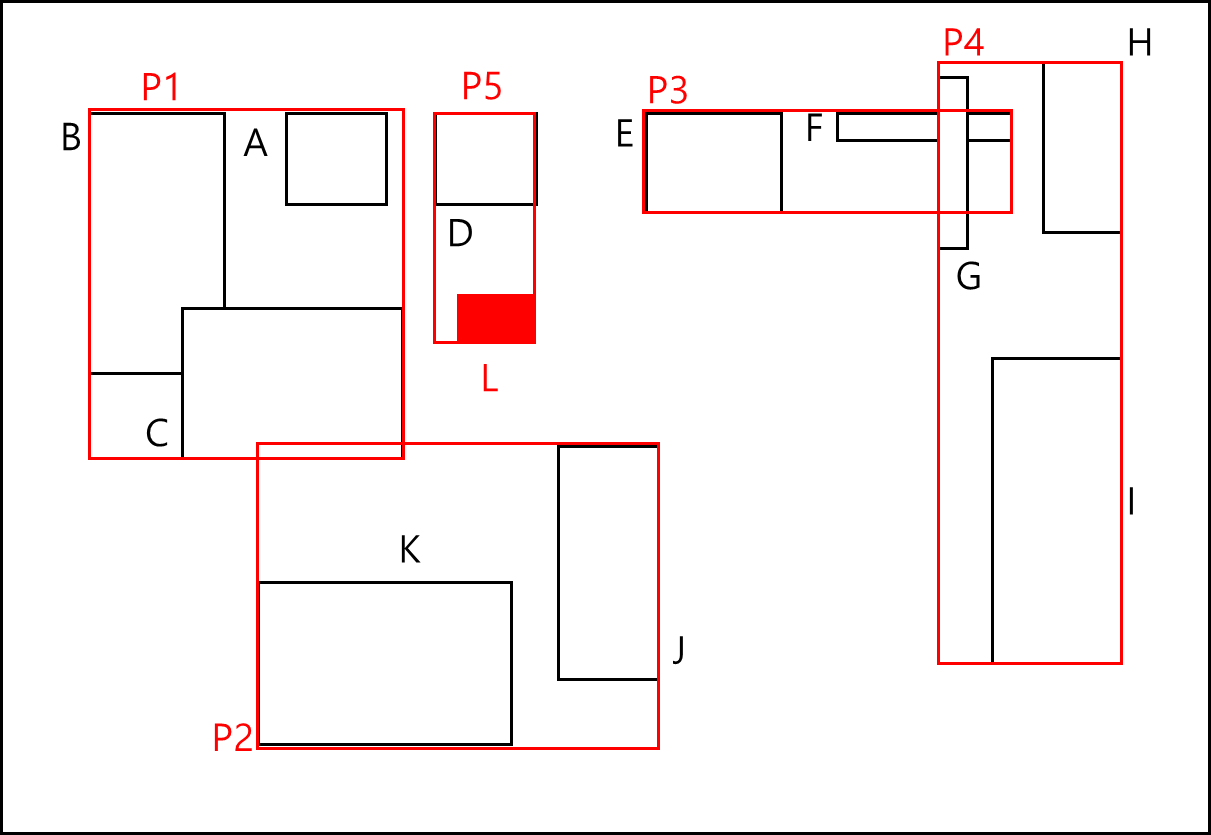
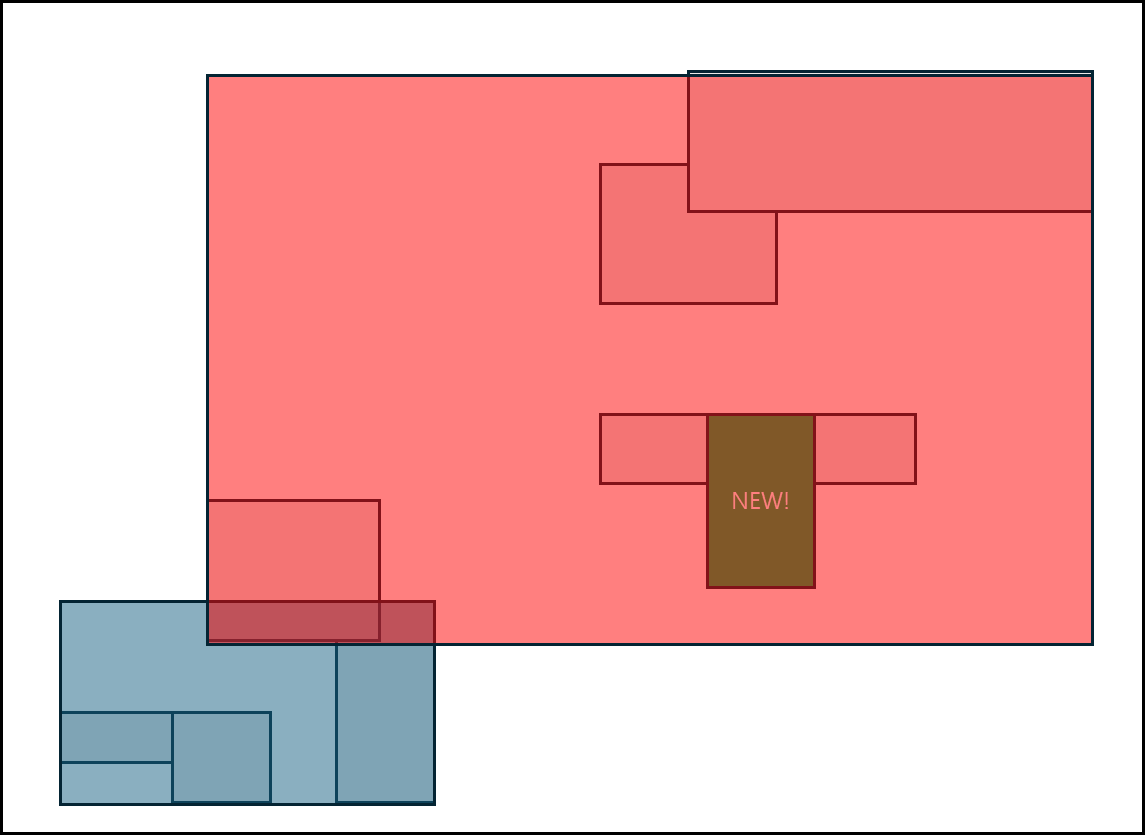
이 경우 아래와 같이 L가 추가된다면
아래와 같이 파티션이 분할되는데
이 경우 P1~P4로 최상위 노드가 꽉 찼으므로 상위 노드를 만들어 해당 노드를 아래와 같이 분할한다.
※ 이미 만들어진 파티션에서 벗어난 위치에 Polygon이 추가된다면?
이미 만들어진 파티션이 가장 적게 확장되는 것을 골라서 파티션의 MBR을 확장한 뒤 해당 Polygon을 추가한다.
ⓒ Split
Index 빌드간 어떻게 파티션을 나누는지, 혹은 Insertion 간에 노드 안에 MBB 개수 제한을 초과할시 어떤 기준으로 나누는지에 대한 내용이다.
그냥 생각해보면 4가지 방식이 있다.
단순 선택(Plane Sweep)
X든 Y든 일정 방향에서 시작해서 순차적으로 검색하여 해당 MBR 안의 전체 POLYGON 개수의 절반 이상을 만나면 만난 순서대로 단순히 묶는다.선형 분할(Linear Split)
먼저 두 개의 seed(시작 그룹)를 빠르게 고르는 규칙(예: 각 축에서 가장 멀리 떨어진 경계들을 찾아 seed로 잡음)로 시작하고, 남은 엔트리들을 “해당 그룹의 MBR이 가장 덜 늘어나는 쪽”으로 하나씩 할당한다.이차 분할(Quadratic Split)
모든 쌍을 검사해서 “같이 있으면 가장 낭비(죽은공간)를 만드는 두 엔트리”를 서로 다른 그룹의 초깃값(seed)으로 선택한다. 그 다음 남은 항목들을 각 그룹에 넣을 때마다 어느 쪽에 넣으면 각 그룹의 MBR 면적 증가가 더 작은지 계산해 할당한다. 선형 분할보다 겹침이 덜한 방식이다.모든 분할 탐색(Exponential Split)
말 그대로 모든 경우의 분할의 탐색 수를 탐색하여 전체 면적 합·겹침을 최소화하는 조합을 찾아서 선택한다.
ⓒ Deletion
특정 Polygon E을 지우기 위해서는 일단 어떤 Leafnode가 대상을 갖고 있는지 찾는다.
그리고 해당 노드에서 E를 지우는데 만약에 E를 지움으로써 해당 Leafnode의 원소가 최소값보다 적어져서 Underflow가 나타나게 된다면 대상 leafnode와 대상 leafnode의 부모 node를 지워버리고 만약 삭제 작업으로 인해 부모가 없는 leafnode가 생겼다면 해당 노드들은 다시 삽입 연산을 통하여 트리에 다시 삽입한다.
ⓓ STR(Sort-Tile-Recursive) — R-tree Packing
STR은 정적(또는 거의 정적인) 객체 집합에서 R-tree를 사전에 잘 채워진(packed) 형태로 생성하는 방법이다. 목적은 잎 노드의 공간 활용률을 최대화하고 MBR(최소 경계 사각형)들의 겹침(overlap)과 여백(coverage)을 줄여 탐색 성능을 향상시키는 것이다. 동적 삽입/삭제가 잦은 경우에는 구조가 훼손되어 성능 저하가 일어날 수 있으므로 정적인 데이터에 적합하다.
각각의 용어를 아래와 같이 정의하겠다.
1
2
3
4
N : 데이터(사각형 또는 객체)의 총 개수
M : 하나의 리프 노드(leaf node)가 수용할 수 있는 최대 엔트리 수 (node capacity)
P = ceil(N / M) : R 트리에서 필요한 리프 노드(MBR)의 최소 엔트리 수(leaf entries)의 수
s = ceil(sqrt(P)) : 세로(vertical) 슬라이스(그룹)과 가로(horizontal) 슬라이스 수 (STR 요구사항)
위 용어를 이용한 알고리즘은 아래와 같다.
1
2
3
4
5
6
7
8
1. 각 객체(또는 객체의 MBR)에 대해 중심점(centroid)을 계산한다.
2. 객체 리스트를 centroid의 x 좌표로 오름차순 정렬한다.
3. 정렬된 리스트를 s = ceil(sqrt(P)) 그룹(세로 슬라이스) 으로 대략 균등 분할한다.
4. 각 세로 슬라이스 내부에서 객체들을 centroid의 y 좌표로 정렬한다.
5. 각 세로 슬라이스에서 정렬된 순서로 연속된 M개씩 묶어(또는 마지막 그룹은 작을 수 있음) 하나의 leaf 엔트리(leaf node)를 만든다.
6. 이때 "각 그룹의 크기 M이 하나의 leaf node를 정의"한다.
7. 이렇게 만들어진 leaf 엔트리들을 새로운 객체 집합으로 보고(각 엔트리는 그들의 MBR을 가짐), 같은 방법(정렬 → 슬라이스 → 그룹화)을 재귀적으로 적용하여 상위 레벨의 노드를 만든다.
8. 루트까지 올라갈 때까지 반복하면 최종 R-tree 완성.
b. R+ -tree
이름에서 알겠지만 R-tree의 파생형이다. 아예 overlap을 허용하지 않는 것으로 overlap이 일어날 경우 아예 split해서 새로운 MBB를 만든다. 이러한 R+ 트리의 경우 느려서 사용되지 않는다.
c. R* -tree
이름에서 알겠지만 이 역시 R-tree의 파생형이다.
삽입시에 MBB의 overlap 증가를 최소화하는 것을 먼저로 두고, overlap 증가가 같다면 면적 증가를 비교하여 선택한다. 삽입 처리 이후 overflow 발생시에 바로 split 하지 않고 강제 재삽입(Forced Reinsert)을 진행하게 된다.
강제 재삽입이란 일부 엔트리를 골라서 부모레벨로 재삽입하여 MBB를 조정하는 방식이다. 만약 재 삽입 이후에도 넘치면 그때는 split을 하게 된다.
아래의 예시를 보자.
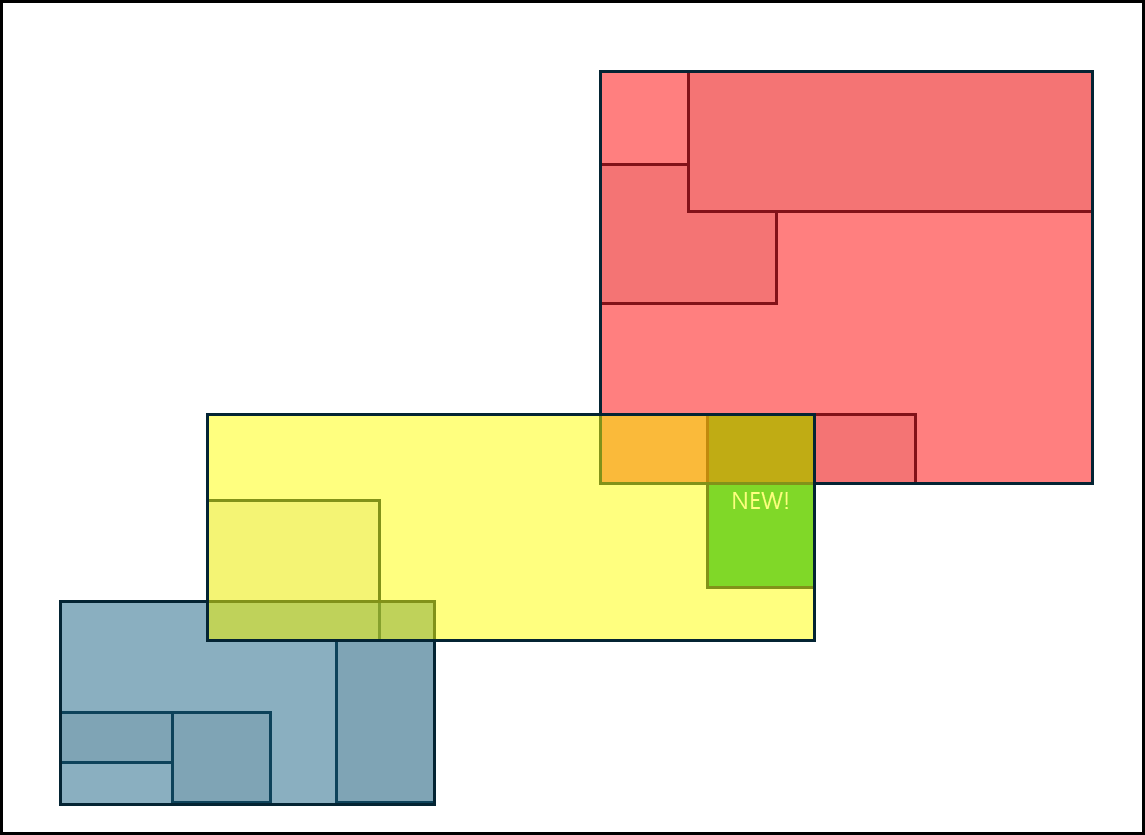
위와 같이 나누어진 MBB가 있다고 해보자. 아래와 같이 초록색의 새로운 polygon이 추가되었다.
그러면 아래의 R-tree방식으로 split하는게 아니라.
아래와 같이 몇 개의 Polygon을 임시로 빼서(R* 논문에서는 30%를 제시) MBB를 재조정 한 뒤 재삽입하는 것이다.
이후에도 Overflow가 일어나면 split을 하게 되는데, 이때도 그냥 split하는게 아니다.
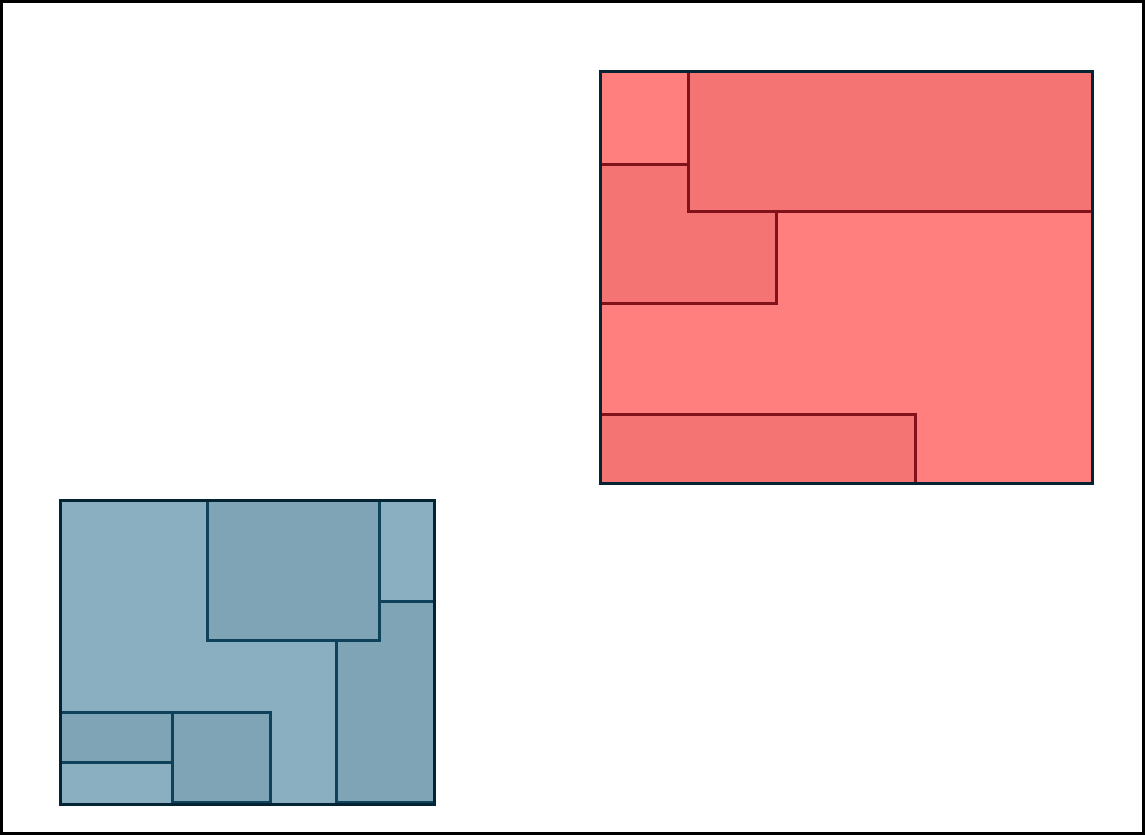
아래와 같은 상황에서 split한다고 할때
아래와 같이 overlap 되는 축이 아닌
overlap이 최대한 덜되는 축으로 split을 하게된다.
참고자료
- Shashi Shekhar and Sanjay Chawla, Spatial Databases: A Tour, Prentice Hall, 2003
- P. RIigaux, M. Scholl, and A. Voisard, SPATIAL DATABASES With Application to GIS, Morgan Kaufmann Publishers, 2002