컴퓨터 구조 - 기본적인 논리회로 - 논리 게이트

논리회로

1. 논리 게이트

하나 이상의 논리적 입력값에 대해 논리 연산을 수행하여 하나의 논리적 출력값을 얻는 전자회로를 말한다.

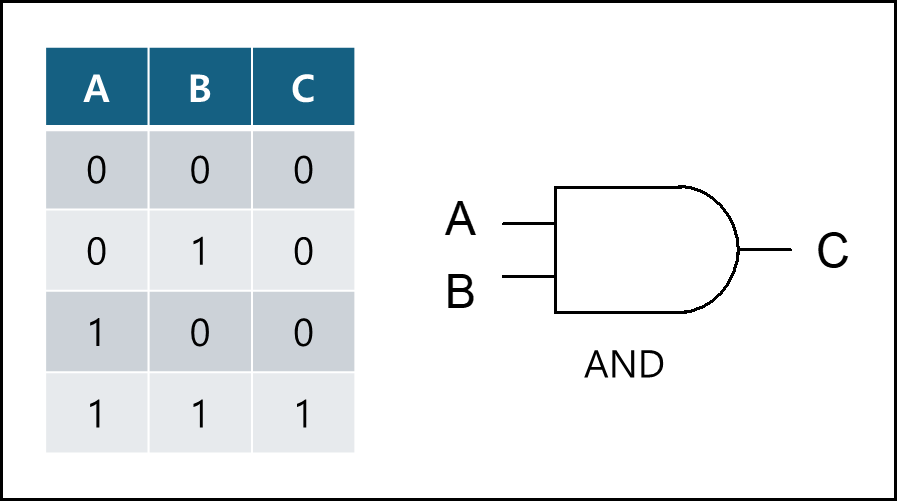
1) 논리곱 - AND

입력값이 모두 1일때만 결과가 1이고 나머지는 0이다.

논리식 표기법 : $C=A\cdot B$

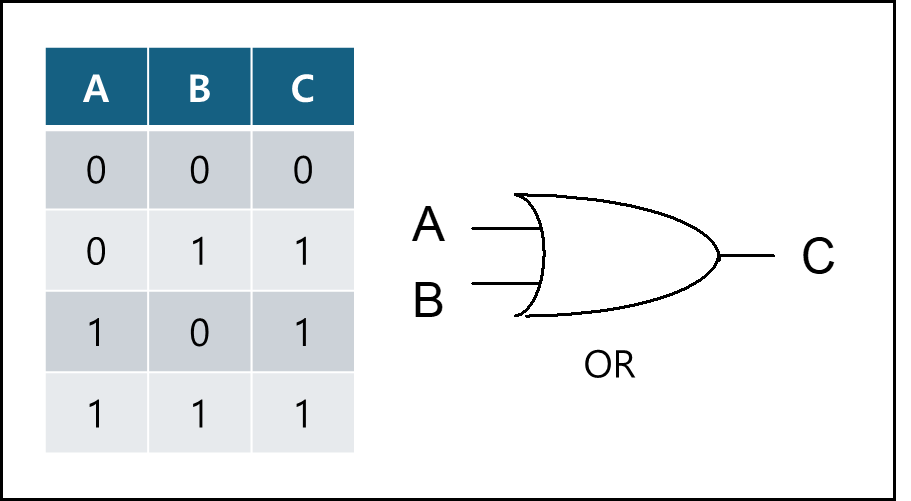
2) 논리합 - OR

입력값 중 하나라도 1이라면 결과가 1이다.

논리식 표기법 : $C=A+B$

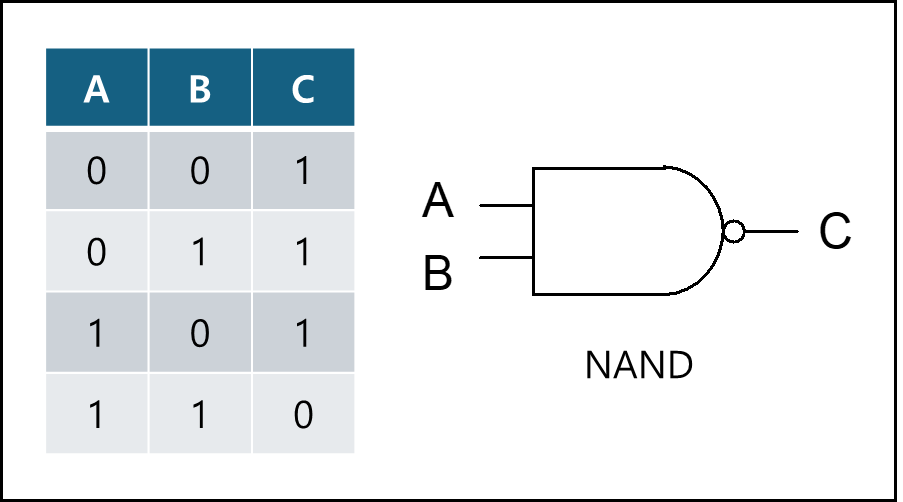
3) 부정 논리곱 - NAND

입력값이 모두 1일때만 결과가 0이고 나머지는 1이다.
AND에서 NOT을 취한 형태이다.

논리식 표기법 : $C=(A\cdot B)’$

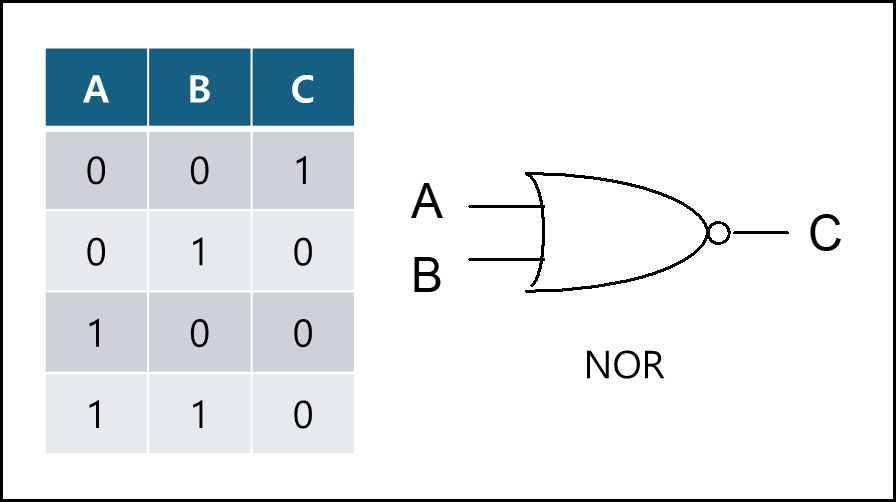
4) 부정 논리합 - NOR

입력값 중 하나라도 1이라면 결과가 0이다.
OR에서 NOT을 취한 형태이다.

논리식 표기법 : $C=(A+B)’$

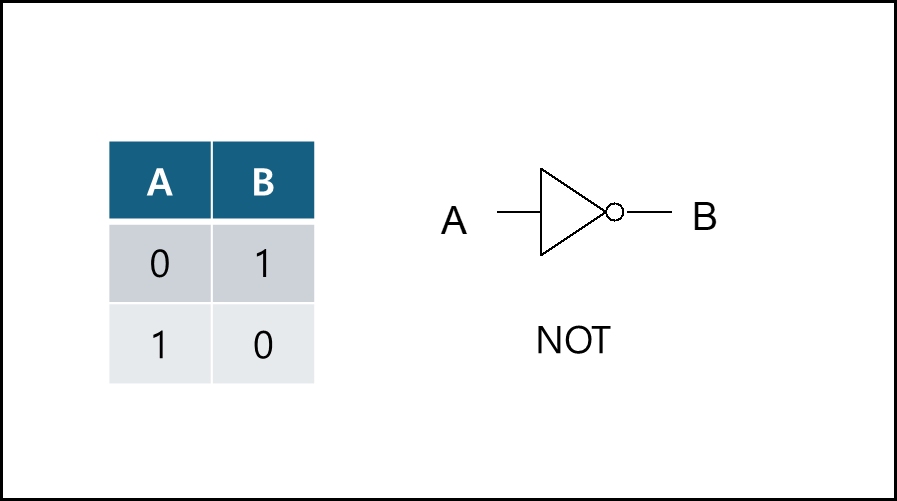
5) 논리부정 - NOT(Inverter)

주어진 입력값을 무조건 반전한다.
논리식 표기법 : $C=A’$

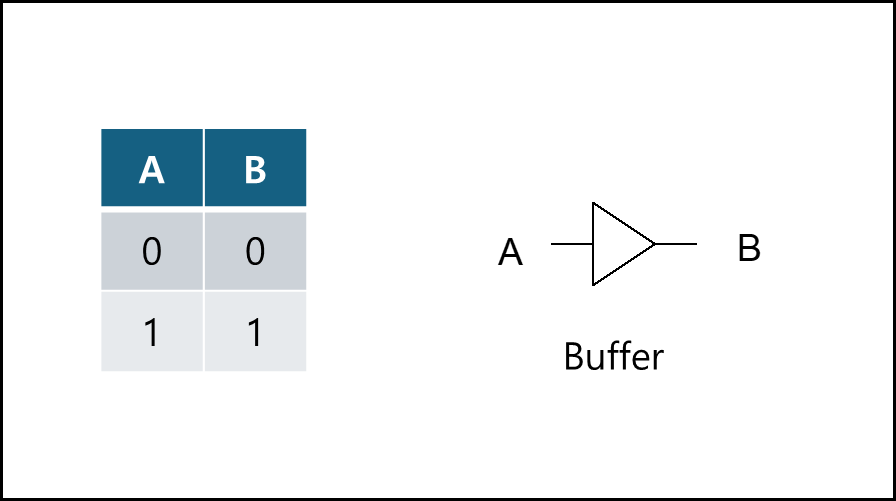
6) Buffer

주어진 값을 무조건 동일하게 반환한다.
논리식 표기법 : $C=A$

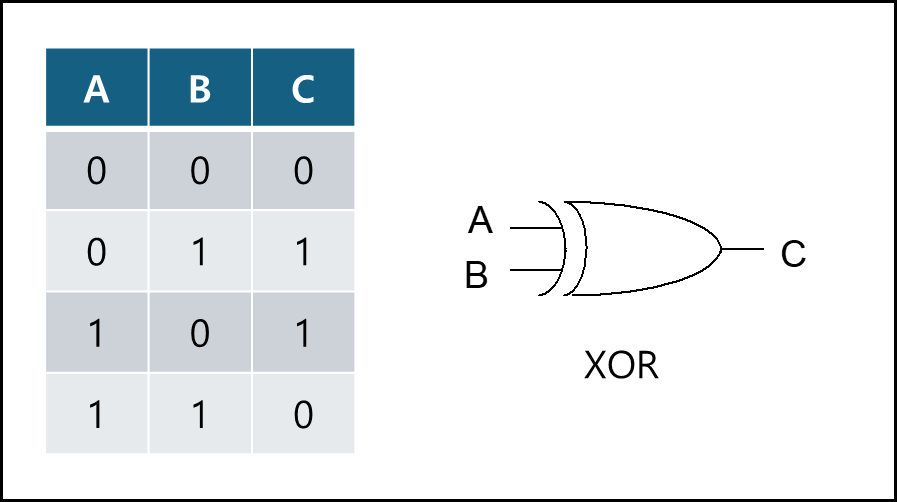
7) 베타적 논리합 - XOR(Exclusive-OR)

주어진 입력 값들중에 1의 개수가 홀수 일때만 결과가 1이다.
논리식 표기법 : $C=A\oplus B$

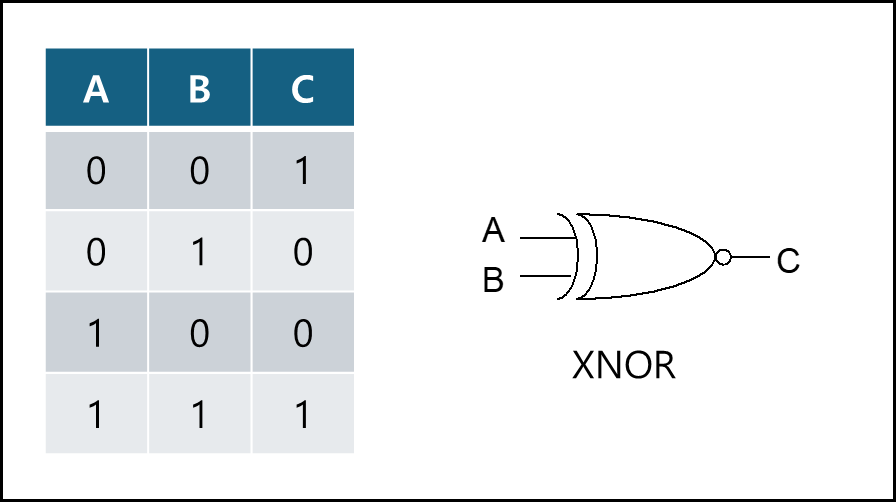
8) 부정 베타적 논리합 - XNOR(Exclusive-NOR)

주어진 입력 값들중에 1의 개수가 짝수거나 0일 때만 결과가 1이다.
XOR에서 NOT을 취한 형태이다.
논리식 표기법 : $C=(A\oplus B)’$

※ INPUT이 3개 이상일 때

NOT과 BUFFER는 INPUT이 1개일 때는 정의되지 않는다.
아래의 진리표는 입력값이 3개일때의 경우이다.

1) AND

INPUT 1	INPUT 2	INPUT 3	OUTPUT
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

2) OR

INPUT 1	INPUT 2	INPUT 3	OUTPUT
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

3) NAND

INPUT 1	INPUT 2	INPUT 3	OUTPUT
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

4) NOR

INPUT 1	INPUT 2	INPUT 3	OUTPUT
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	0

5) XOR(Exclusive-OR)

INPUT 1	INPUT 2	INPUT 3	OUTPUT
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

6) XNOR(Exclusive-NOR)

INPUT 1	INPUT 2	INPUT 3	OUTPUT
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

참고자료

• 위키백과 - 논리 회로
• 위키백과 - XNOR 게이트