컴퓨터 구조 - 메모리 구조에 따른 소프트웨어 최적화
메모리 구조에 따른 소프트웨어 최적화
1. 개요
최근 컴파일러에는 대부분 포함되어있는 내용이다. 메모리 구조와 Cache 구조에 따른 최적화 기법인데, 기본적으로 아래의 목적을 가지고 실행 된다.
- Temporal locality 증가
- Spatial locality 증가
- Conflict 제거
위 세 가지를 만족하는 방향으로 조정하면 성능이 올라가게 된다. 여기서 성능이 올라간다는 것은 응답 시간이 줄어든 다는 뜻이다.
코드 최적화란 위 세 가지를 목표로 원래 코드에서 메모리 layout과 접근 순서를 변경함으로써 성능을 높이는 것이다.
2. 효과적인 코드를 만드는 절차
1) 좋은 알고리즘을 사용한다.
어떤 배열을 정렬한다고 해보자. bubble sort와 quick sort로만 비교해도 엄청나게 차이나는 것을 알 수 있다.
2) 효과적인 라이브러리를 사용한다.
유명한 라이브러리들은 대부분 좋은 알고리즘을 사용한다. 특히 해당 머신에 특화되어 최적화되어있는 경우도 많다.
3) 적절한 컴파일러와 옵션을 사용한다.
기본값으로 어느정도 최적화를 지원하는 것도 있고 별도의 옵션으로 지원하기도 한다.
실제로 동일한 c 코드를 놓고 visual studio에서 빌드를 했을 때 기본값으로 빌드하는 것과 완전 최적화 옵션을 끄고 빌드하면 생성된 바이너리 코드가 다른 것을 알 수 있다.
4) 코드를 수동으로 최적화 한다.
예전 방식이다. 하지만 여전히 효과적이고 프로그래머의 실력에 좌우된다.
3. 반복문 최적화
기본적으로 캐시 최적화라고하면 Loop와 Array에서 진행된다. 이는 Locality를 잘 살릴 수 있고, 이를 통해 성능 이득을 보기 쉽기 때문이다.
모든 최적화가 그렇지만 바꾼 코드가 이전 코드와 동일한 결과를 출력하는지는 좀 봐야한다.
1) Loop Interchange
1
2
3
4
5
6
7
// Loop 1
char a[N][N];
for(j=0;j<N;j++) {
for (i<0;i<N;i++) {
a[i][j]++;
}
}
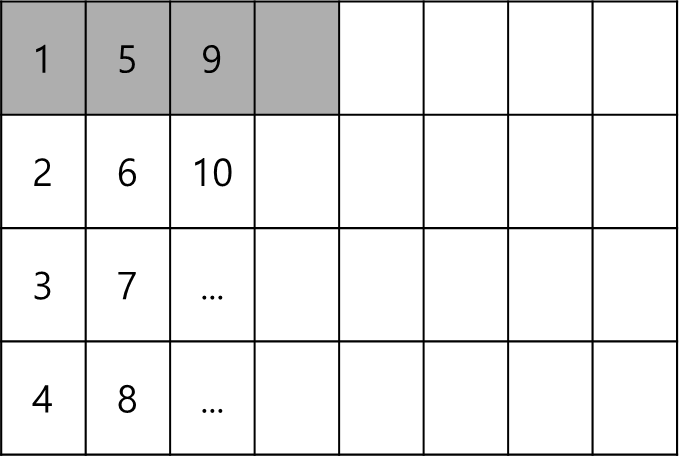
위의 코드는 Spatial Locality 면에서 볼때 매우 좋지 않다. 이는 위의 코드의 메모리 엑세스 패턴이 아래와 같기 때문이다.
회색 음영으로 칠한 부분이 Cache miss로 인해 갖고 온 블럭이라고 할 때 갖고온 Cache 부분이 아닌 다른 부분을 접근하기 때문에 또 Cache miss가 나게 된다.
위와 같은 형태라면 100% Cache miss가 나게 된다. (5번에 엑세스할때쯤 이미 캐시가 Replacement 되어있을 가능성이 있기 때문에)
따라서 행동은 동일하되 빠른 성능을 위해서는 아래와 같이 코드를 바꿔야한다.
1
2
3
4
5
6
7
// Loop 1
char a[N][N];
for(i=0;i<N;i++) {
for (j<0;j<N;j++) {
a[i][j]++;
}
}
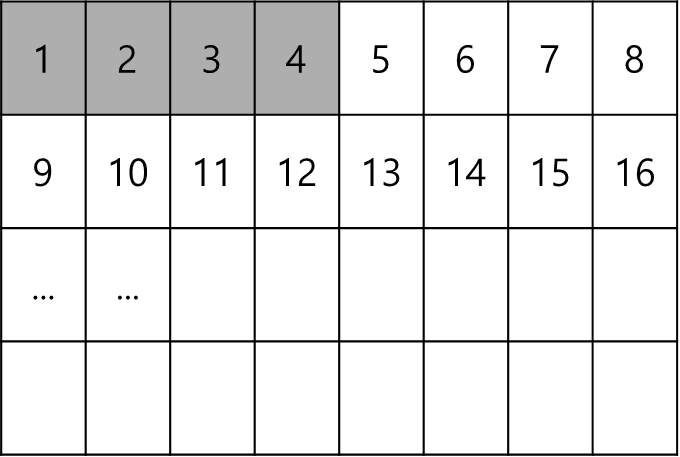
회색 음영이 갖고 온 캐시라고 할때 접근 순서와 동일하게 맞아떨지는 것을 알수 있으며 100% Cache miss때와는 다르게 Cache hit가 어느정도 일어나기 때문에 성능이 더 향상된다.
2) Loop Fusion
1
2
3
4
for(i=0;i<N;i++)
a[i] = b[i] + 1;
for(i=0;i<N;i++)
c[i] = 3*b[i];
위의 코드의 경우 두 개의 loop간에 Temporal Locality 를 전혀 쓸 수 없다.
자세히보면 첫번째 루프의 b[i]와 두번째 루프의 3*b[i]는 동일한 인덱스이기 때문에 Temploral Locality를 살릴 수 있는데 말이다.
따라서 성능 향상을 위해 아래와 같이 바꿀 수 있다.
1
2
3
4
for(i=0;i<N;i++) {
a[i] = b[i] + 1;
c[i] = 3*b[i];
}
3) Loop Reversal
1
2
3
4
5
6
for(i=0;i<N;i++) {
a[i] = b[i] + 1;
c[i] = 3*b[i];
}
for(i=0;i<N;i++)
d[i] + c[i+1] + 1;
이전의 Index에서 처리한 값이 이후 Index에서 처리될 값에 영향을 주지 않는다 (즉, loop carried dependency 가 없다) 따라서 순서를 바꿔도 상관없으며 Cache Miss 또한 영향을 받지 않는다. (block 끝부분에서 갖고 올것이므로)
1
2
3
4
5
6
for(i=N-1;i>=0;i--) {
a[i] = b[i] + 1;
c[i] = 3*b[i];
}
for(i=N-1;i>=0;i--)
d[i] + c[i+1] + 1;
일단 분리하기는 했으나 cache의 way만 충분하고 초기값 처리만 해준다면 두 개의 loop를 합쳐도 무방할 것이다.
4) Loop Fission
1
2
3
4
5
for(i=0;i<N;i++) {
a[i] = b[i] + 1;
c[i] = 3*a[i];
f[i] + g[i] + h[i];
}
만약 4-way cache를 쓰고 있다고 가정해보자.
동일한 Index의 값들을 동일한 cache index에 위치할 가능성이 높다.
따라서 위와 같이 4개를 넘어서는 변수는 4-way cache내에서 conflict miss를 일으킬수 있다. 이런 경우 차라리 Loop를 분할 해주면 cache conflict 없이 오히려 성능이 항샹 될 수 있다.
1
2
3
4
5
6
7
for(i=0;i<N;i++) {
a[i] = b[i] + 1;
c[i] = 3*a[i];
}
for(i=0;i<N;i++)
f[i] + g[i] + h[i];
5) Loop Unrolling
Loop를 뜯는 행동이다. 아래의 코드를 보자.
1
2
for (i=0;i<100;i++)
a[i] = b[i] + c;
위 코드를 아래로 뜯는 것이다.
1
2
3
4
for (i=0;i<100;i++) {
a[i] = b[i] + c;
a[i+1] = b[i+1] + c;
}
위와 같은 경우 여러가지 이득과 손해가 있다.
a. 이득
- Loop overhead가 줄어든다(branch taken에 대한 계산과 index 계산등)
- 명령어가 늘어나기 때문에 현대 superscalar 머신에서 좀더 효율적이다.
b. 손해와 한계
- Renaming을 위한 더 많은 레지스터가 필요하다.
- 코드 사이즈가 커진다(용량을 많이 먹음)
- loop carried dependency는 해결할 수 없다.
- loop내에 if가 있으면 성능이 떨어진다.
4. 배열 최적화
1) Array Merging
아래의 코드를 보자
1
2
3
int a[N], b[N], c[N]
for(i=0;i<N;i++)
a[i] = b[i] + c[i];
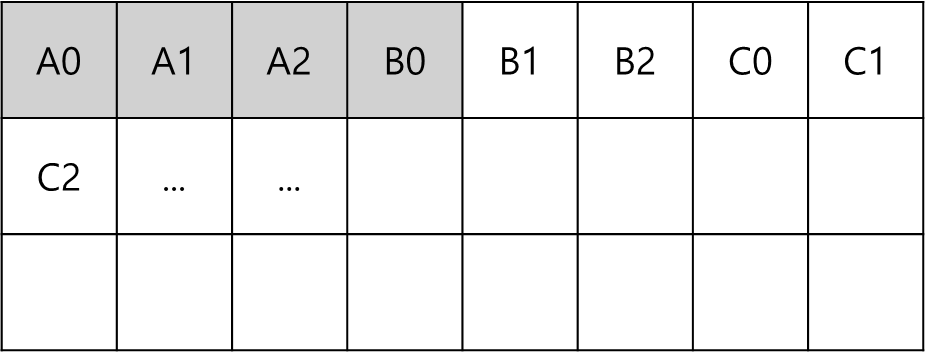
위와 같이 배열을 잡을 경우 연산과 배열 할당에 문제가 생길 수 있다. 가령 N이 3이고, 캐시에서 한번에 가져올때 4 x sizeof(int)를 가져온다고 가정해보자.
연산은 0부터 해야하는데 B0까지는 있다고 해도 C0는 다시 갖고 와야한다.
매우 비효율적이다. 따라서 아래와 같이 할당해두면 좀 더 효율적이다.
1
2
3
4
5
struct ALL {int a,b,c};
struct ALL M[N]
int a[N], b[N], c[N]
for(i=0;i<N;i++)
M[i].a = M[i].b + M[i].c;
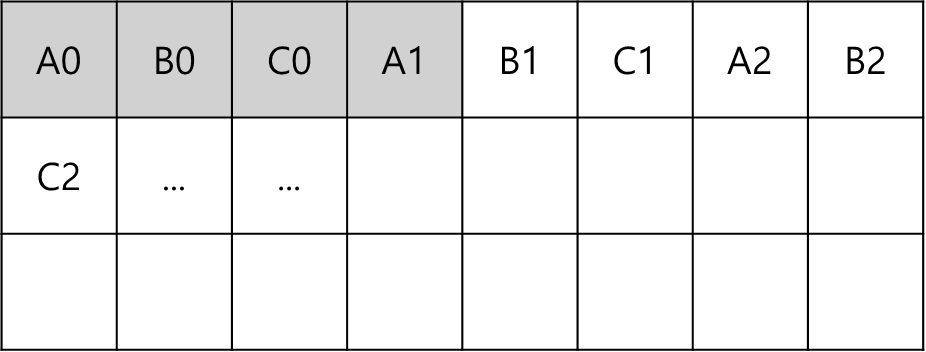
Spatial Locality가 증가했음을 알 수 있다.
2) Array Padding
기본적으로 컴퓨터의 메모리 구조는 align을 맞추면 좋다.
하지만 Cache 입장에서는 아닐 수 있다. 아래의 코드를 보자
1
2
3
int a[N], b[N];
for(i =0 ;i<N;i++)
sum += a[i]*b[i];
이 코드가 뭐가 문제인데 할 수 있다.
일단 L1 cache가 2-way면 문제가 없다. 하지만 대부분 L1 Cache의 경우 빨라야하기 때문에 Direct mapped cache 방식을 차용한다.
그렇게 되면 동일한 index를 가진 값들은 conflict miss가 날수 있다.
따라서 a와 b값의 할당시 약간의 틀어짐을 추가해주면 cache miss가 나지 않을 수 있다.
1
2
3
int A[N], pad[8], B[N];
for(i =0 ;i<N;i++)
sum += a[i]*b[i];
32bytes 만으로 캐시 miss를 줄일 수 있다면 꽤 싸게 먹히는 것 같다.
5. 행렬 곱셈 최적화
정확하게는 2차원 배열 곱셈이라고 볼 수 있다.
여기서 N x N의 정방행렬을 가정하며 이 N은 매우 큰 값이고. 캐시는 이 모든 값을 담을 정도로 충분히 크지 않으며, 라인 사이즈 하나가 32Bytes라고 가정한다. 아래의 코드를 보자
1
2
3
4
5
6
7
8
for (i=0;i<n;i++){
for (j=0;j<n;j++) {
sum = 0.0;
for (k=0;k<n;k++)
sum += a[i][k] * b[k][j]; // inner most loop
c[i][j] = sum;
}
}
$ N \times N $ 크기의 행렬끼리 곱하는 예제이다. 시간 복잡도는 $ O(N^{3}) $ 이다.
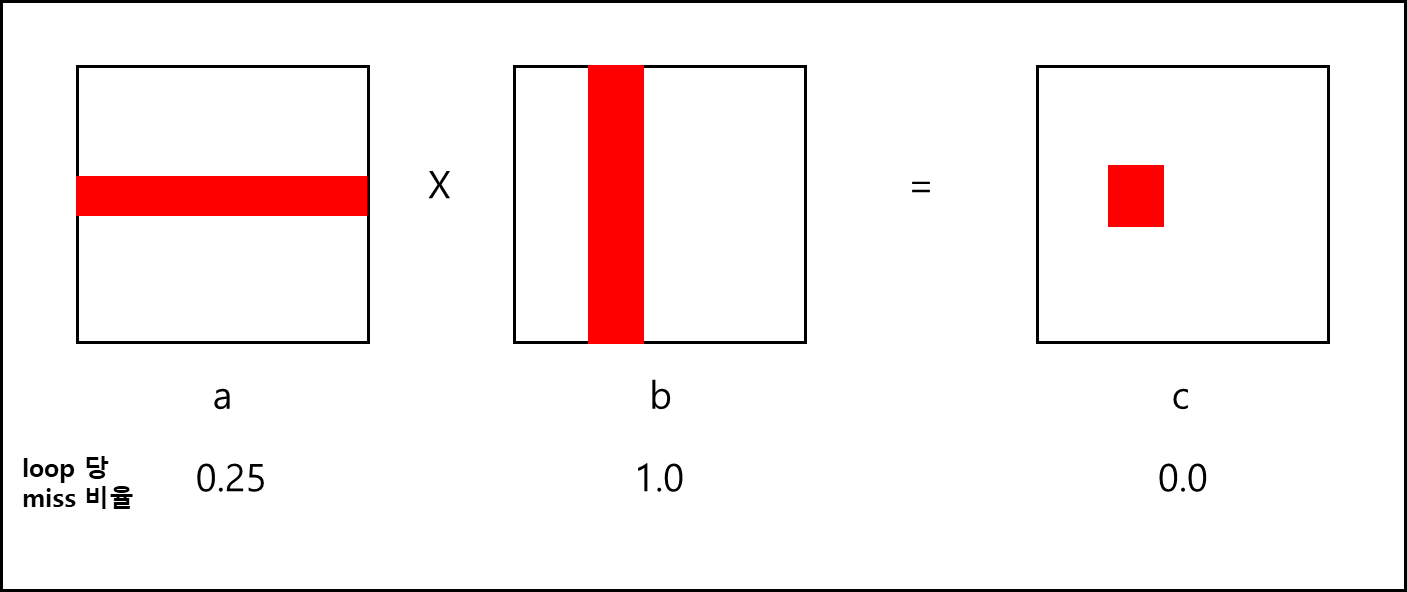
옆에 별도로 주석 처리 되어있는 코드를 기준으로 연산을 살피면 아래와 같다.
row-wise로 엑세스를 하면 block에 대해서 4번에 1번은 cache miss가 나므로 0.25, column-wise하게 엑세스를 하면 모든 엑세스에 대해서 cache miss가 나므로 1.0, 그리고 한번 엑세스해서 쓰고 말기 때문에 0.0 이다
바깥부터 접근하는 변수명으로 해당 방식을 명명할때 “ijk” 방식이라고 할 수 있는데 위와 같은 패턴을 보이는건 “jik”도 동일하다.
1
2
3
4
5
6
7
8
for (j=0;j<n;j++){
for (i=0;i<n;i++) {
sum = 0.0;
for (k=0;k<n;k++)
sum += a[i][k] * b[k][j]; // inner most loop
c[i][j] = sum;
}
}
동일한 패턴에 동일한 miss 비율을 보인다. “ijk”, “jik”를 포함하여 나올 수 있는 모든 패턴은 총 6개이다.
그리고 나머지 4개도 위의 두 경우와 같이 페어를 이루어 동일한 패턴을 보인다.
아래와 같은 “kij”,”ikj”를 생각해보자.
1
2
3
4
5
6
7
8
// kij
for(k=0;k<n;k++){
for(i=0;i<n;i++){
r=a[i][k];
for(j=0;j<n;j++)
c[i][j]+=r*b[k][j];
}
}
1
2
3
4
5
6
7
8
// ikj
for(i=0;i<n;i++){
for(k=0;k<n;k++){
r=a[i][k];
for(j=0;j<n;j++)
c[i][j]+=r*b[k][j];
}
}
코드가 조금 바뀌어 헷갈릴 수 있지만 결국엔 동일한 연산을 하는 코드이다.
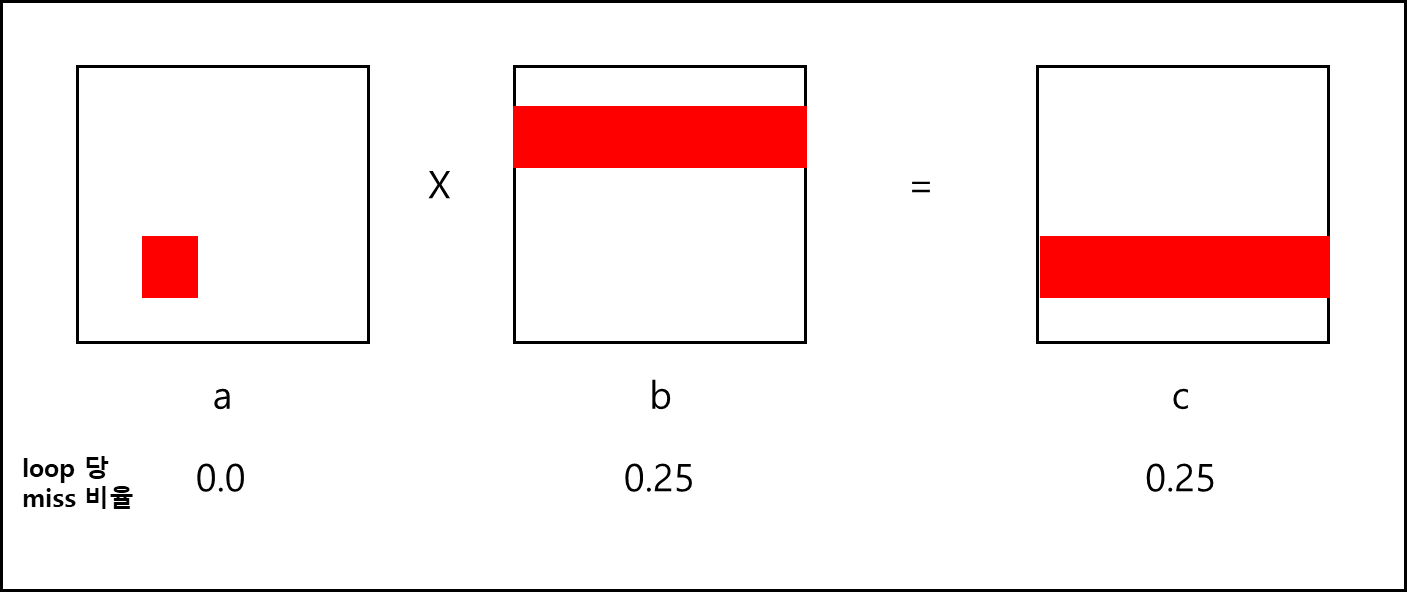
위와 같은 패턴은 아래와 같은 접근 패턴을 보인다.
나머지 한 페어는 “jki”, “kji”이다
1
2
3
4
5
6
7
8
//jki
for(j=0;j<n;j++){
for(k=0;k<n;k++){
r=b[k][j];
for(i=0;i<n;i++)
c[i][j]+=a[i][k]*r;
}
}
1
2
3
4
5
6
7
8
//kji
for(k=0;k<n;k++){
for(j=0;j<n;j++){
r=b[k][j];
for(i=0;i<n;i++)
c[i][j]+=a[i][k]*r;
}
}
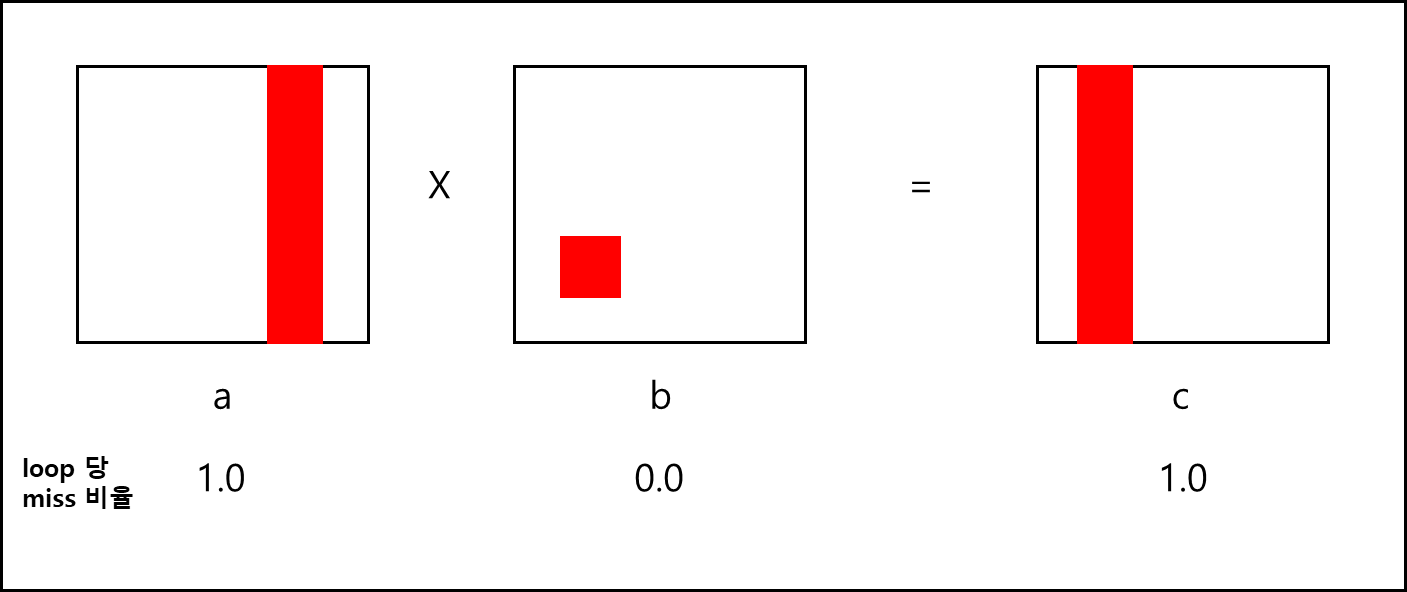
위 페어는 아래와 같은 접근 패턴을 보인다.
이렇게 보면 “kij”,”ikj” 조합이 cache miss 비율 합계까 0.5이기 때문에 가장 성능이 좋을 것 같다.
그런데 여기서 한 가지 더 고려해봐야할 것이 있다.
바로 메모리 엑세스 빈도이다. inner most loop에서 load/store 를 몇 번이나 했는가에 대해 생각해봐야하는 것이다.
- ijk, jik : 2 loads, 0 stores
- kij,ikj : 2 loads, 1 stores
- jki,kji : 2 loads, 1 stores
여기서 += 연산간에 특정 변수에다가 쓰냐 혹은 2차원 배열내에 쓰냐는 중요한데 일반 변수를 선언해서 쓸 경우 이는 register로 할당될 가능성이 높기 때문에 store로 치지 않는다. 따라서 ijk가 0 stores로 간주되는 것이다.
그렇다면 store가 한번 더 적은 ijk,jik 조합이 제일 빠를까? 그렇지 않다. 실질적으로 벤치마크를 돌려보면 일정 N개 이상에서는 kij,ikj 페어가 제일 빠른 것을 알 수 있다.
여기서 일정 N이란 Temporal Locality와 Sptial Locality의 trade-off 지점이다.
교재에서는 약 N이 150정도로 잡히는데 이는 cache 구조와 크기에 따라 달라질 수 있다.
이렇게 특정 지점에서는 Spatial Locality 혹은 Temporal Locality만 선택하는 것이 아닌 둘다 사용할 수는 없을까 하는 생각을 누군가가 했고, 누군가는 그 방법을 찾아냈다.
그 방법은 가장 기본적인 방법인 divide and conquer 였다.
기본적으로 모든 행렬의 곱셉은 분할 할 수 있다. 가령 아래와 같은 배열이 있다고 해보자.
\[\begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix} \times \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix} = \begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix}\]그러면 아래와 같은 식으로 분할 할 수 있다.
\(C_{11} = A_{11}B_{11}+A_{12}B_{21}\) \(C_{12} = A_{11}B_{12}+A_{12}B_{22}\) \(C_{21} = A_{21}B_{11}+A_{22}B_{21}\) \(C_{22} = A_{21}B_{12}+A_{22}B_{22}\)
위의 식을 기반으로 행렬 곱셈 코드를 수정하면 아래와 같이 변한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
for(jj=0;jj<n;jj+=bsize){
// 초기값 처리 시작
for(i=0;i<n;i++){
for(j=jj;j<min(jj+bsize,n);j++)
c[i][j]=0.0;
// 초기값 끝
for(kk=0;kk<n;kk+=bsize){
for(i=0;i<n;i++){
for(j=jj;j<min(jj+bsize,n);j++){
sum=0.0;
for(k=kk;k<min(kk+bsize,n);k++){
sum+=a[i][k]*b[k][j];
}
c[i][j]+=sum;
}
}
}
}
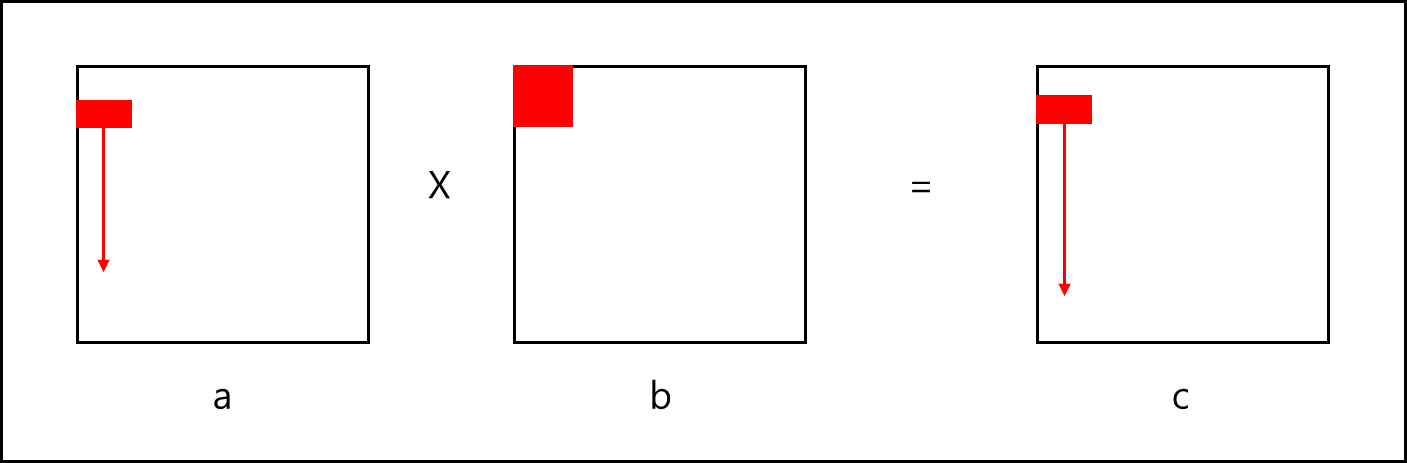
위 코드는 아래의 엑세스 패턴을 가진다.
이 경우 column-wise로 움직여도 해당 데이터가 cache block 단위로 연산되기 때문에 한번 갖고온 cache 데이터는 모두 사용하여 Spatial Locality가 극대화되고, b의 전체 블럭은 계속해서 재사용되기 Temporal Locality가 극대화된다.
따라서 위의 방식대로 코드가 구동되면 가장 성능이 좋다.
참고자료
- Computer Organization and Design-The hardware/software interface, 5th edition, Patterson, Hennessy, Elsevier
- 서강대학교 이혁준 교수님 강의자료 - 고급 컴퓨터 구조