통계학 - 로지스틱 회귀 분석
로지스틱 회귀분석
1. 개요
일반적인 선형회귀는 표본이 양적자료일때 사용했었다. 하지만 질적자료(범주형 자료라고도 불린다)일 경우에는 일반적인 선형 회귀를 적용하기 어렵다. 이는 결과값이 $ (-\infty , \infty )$로 나타나기 때문이다. 따라서 반응 변수 값이 0 또는 1로 나타나는 이진 변수나 혹은 1,2,3 등으로 제한되는 여러개로 나타나는 멀티 변수의 경우는 사용할 수 없다.
따라서 선형 회귀 모델을 적절하게 변경하여 분석자가 원하는 형태의 값을 출력하게 해야한다. 이진 변수의 경우 0과 1사이의 값으로, 멀티 변수의 경우 제한되는 여러개의 값 형태로 말이다.
2 종류
1) 이항 로지스틱 회귀(Binomial Logistic Regression)
종속변수 결과가 2개의 범주인 경우이다.
ex) 성공, 실패
2) 다항 로지스틱 회귀(Multinomial Logistic Regression)
분화 로지스틱 회귀(Polytomous Logistic Regression)이라고도 불린다.
종속변수 결과가 2개 이상의 범주인 경우이다. ex) 서울, 대전, 대구, 부산
3) 서수 로지스틱 회귀(Ordinal Logistic Regression)
종속변수 결과가 2개 이상의 범주이되 순서가 존재하는 경우이다.
ex) 성적 A,B,C
3. 분석 원리
여기서는 이항 로지스틱 회귀의 원리에 대해서 설명해보도록하겠다.
이항 로지스틱 회귀 분석을 이용하려면 결과값, 즉 종속변수가 0에서 1 사이값이 나타나야한다. 개요에서 언급했듯이 질적자료에서 일반적인 선형회귀 방식을 사용하려면 특정한 변환이 필요하다고 했다. 여기서 필요한게 오즈(Odds)와 로짓변환(Logit)이라는 개념이다.
1) 오즈(Odds)
어떤 사건이 일어날 확률을 그 사건이 일어나지 않을 확률로 나눈 값이다.
가령 어떤 확률이 일어날 확률이 0.6이라 할때 오즈 값은 0.6/0.4이므로 1.5로 나타난다.
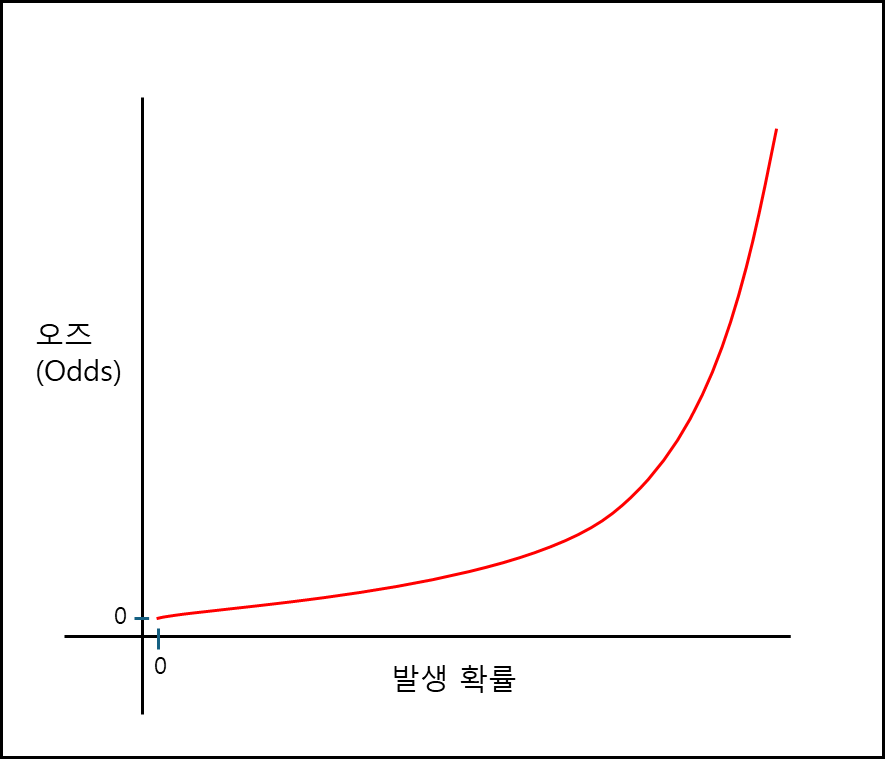
모든 확률은 0에서 1사이이므로 이를 그래프로 나타낸다면 다음과 같다.
위의 그래프와 같이 오즈 값의 범위는 $(0 , \infty )$로 나타나게 되며 식으로 나타내면 아래와 같다.
\[Odds(Y=1) = \frac{p}{1-p}\]여기서 p는 일어날 확률이다.
2) 로짓 (Logit)
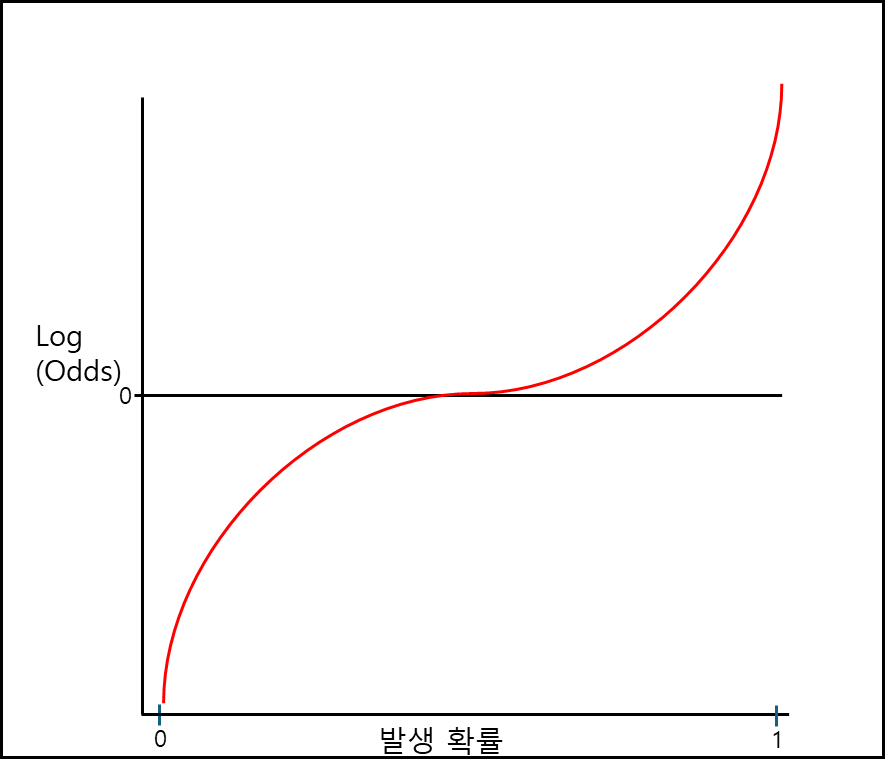
간단히 말해서 오즈에 로그를 취한 값이다. 그러면 비대칭적이던 값이 대칭으로 변하고 그래프의 형태는 아래와 같이 변한다.
확률 0에서 1에 따라 $(- \infty , \infty )$로 나타나게 된다. 수식으로 나타내면 아래와 같다.
\[Logit(p) = log(odds) = log \frac{p(X)}{1-p(X)} = \beta_{0} + \beta_{1}X_{1} + ... + \beta_{k}X_{k}\]우리가 원하는 결과는 설명 변수의 값에 따라 종속 변수의 값이 0에서 1사이 값이 나타나는 것을 원하므로 추가적인 처리를 해준다.
3) 로지스틱 함수(Logistic Function)
위의 로짓을 역함수로 해주면 우리 원하는 값이 나오게된다.
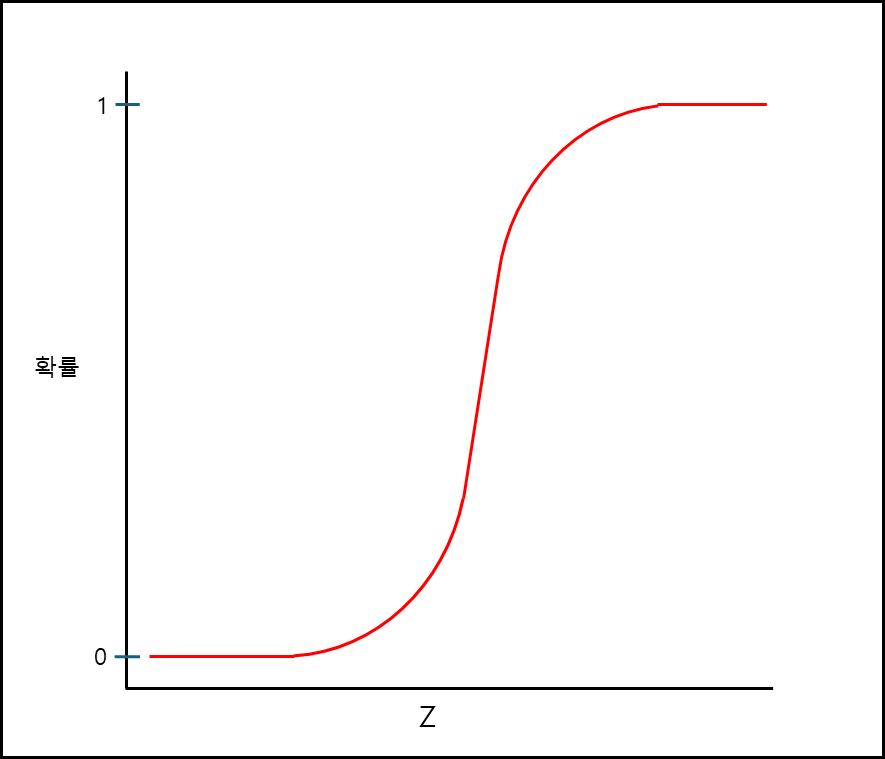
입력값이 어떤 값이 들어가든, 출력 값이 0에서 1사이로 나타나는 아래와 같은 함수가 된다.
수식으로 나타내면 아래와 같다.
\[Logit(p)^{-1} (\beta_{0} + \beta_{1}X_{1} + ... + \beta_{k}X_{k}) = \frac{1}{1+exp^{-(\beta_{0} + \beta_{1}X_{1} + ... + \beta_{k}X_{k})}} = Logistic(z) = \frac{1}{1+exp^{-z}}\]이를 로지스틱 함수라고 하며 이항 로지스틱 회귀 분석에서 사용하는 함수이다.