통계학 - 선형 회귀 분석
선형회귀분석
1. 단순 선형 회귀 분석
1) 필요한 정의
a. 참 모형
실제 전체 모든 경우를 포함한 모형 (현실세계에서는 불가)
b. 설정모형
자료를 보고 임의의 형태를 대략적으로 표기한 모형
c. 적합모형
자료에서 가장 적합한 형태로 설정 모형을 조정한 모형
2) 단순 선형 회귀 모형
일차 방정식 형태로 나타나는 모형으로 직선 회귀 모형이라 불리기도 한다.
형태는 아래와 같다.
- Y : 반응변수 (Response variable), 종속변수 (Dependent variable)
- X : 공변량, 설명변수 (covariates)
- $\varepsilon$ : 오차항(Error term), 흔히 $\varepsilon \sim N(0,\sigma^{2})$이라고 가정
- $\beta_{0},\beta_{1}$ : 회귀계수 (regression coefficients), 추정해야할 모수이다.
a. 목표
3개의 모수, $\beta_{0},\beta_{1},\sigma^{2}$를 추정하는 것
이를 위해서 n개의 자료를 관측하며 해당 자료는 다음과 같이 표기한다.
\[(X_{i},Y_{i}), i=1,2,...,n\]각 자료에 대한 것을 식으로 나타내면 아래와 같다.
\[Y_{i} = \beta_{0} + \beta_{1}X_{i} + \varepsilon_{i}, i=1,2,...,n\]b. 목표를 구하는 방법 - 최소제곱추정
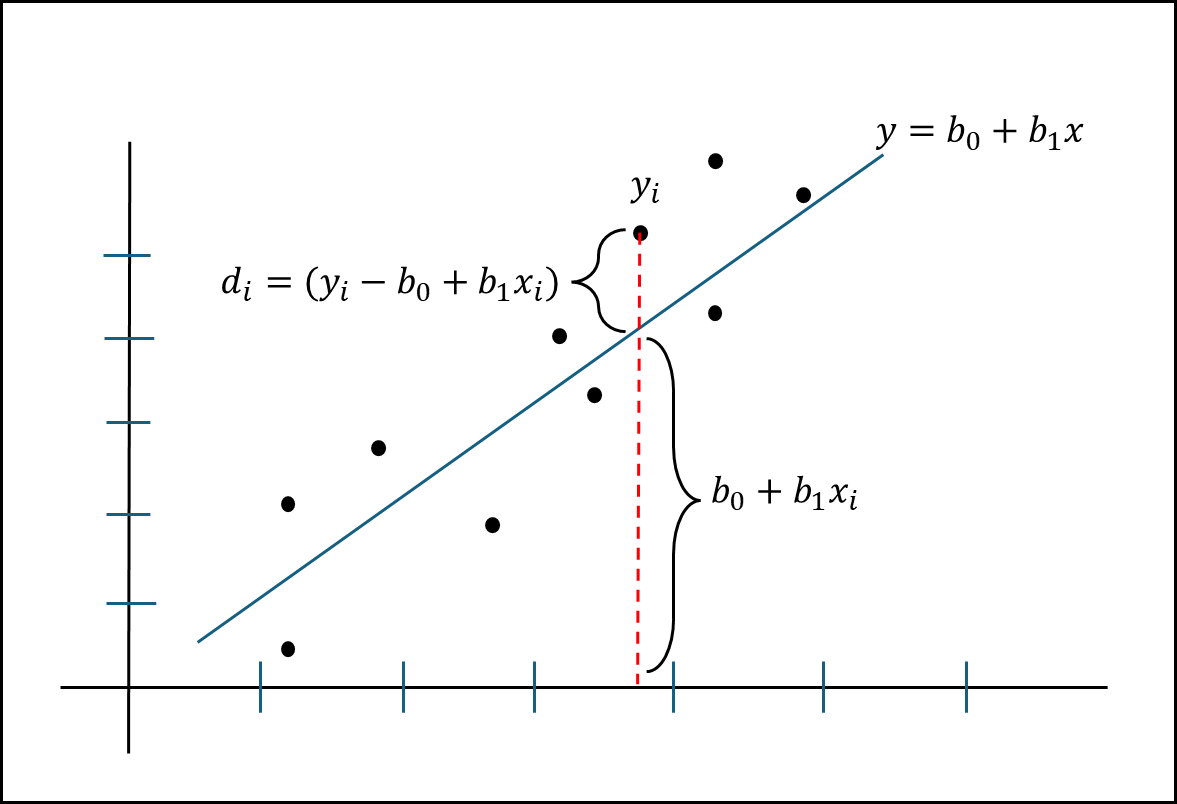
아래와 같은 모형이 있다고 가정해보자
산포도 위에 임의로 지정한 모형이 있고 산포도 점과 모형간에 거리를 아래와 위의 그림의 식과 같이 정의할 수 있다.
여기서 모든 점들은 $d_{i}$ 값들을 가질 수 있는데 이러한 $d_{i}$값들의 합이 최소가 된다면 해당 모형은 현재 산포도에서 적합 모형이라 부를 수 있다.
일차 방정식의 경우 기울기와 y절편 값만 있다면 해당 그래프를 그려낼 수 있는데 이 경우 기울기는 $b_{1}$, y 절편은 $b_{0}$이다. 이 값을 적절히 조정할 경우 모든 점의 X 값을 넣어도 최소 오차합이 나타나게 만들 수 있다. 여기서 오차를 더할 때는 제곱해서 더한다. 따라서 오차의 제곱의 합이 최소 인 경우를 찾아서 구하는 것이므로 이 방법을 최소 제곱 추정법(LSE, Least Squares Estimation)이라 한다.
여기서 최소 제곱을 추정하기 위해서는 각 Beta값 두 개를 각각 편미분해야한다. 정확하게는 두번 미분해서 Hassian Matrix를 계산해서 최소값인지 최대값인지 확인해야한다.
(부가설명 : 미분을 한다는 것은 기울기를 구한다는 것이다. 두번 미분한다는 건 이계도함수를 구한 다는 것이고 이계도 함수를 이용하여 최소값을 구할 수 있다)
원래는 그렇게 해야하는데, 내가 들은 강의에서는 일단 $\beta_{0},\beta_{1}$에 대해서 각각 편미분하고 각 값을 0으로 두어 연립 방정식으로 계산하는 방식을 차용했다.
해서 각각의 최소 제곱 추정량은 아래와 같다.
$\beta_{0}$의 최소제곱추정량 : \(\hat{\beta}_{0} = \overline{Y}-\hat{\beta}_{1}\overline{X}\)
$\beta_{1}$의 최소제곱추정량 : \(\hat{\beta}_{1} = \frac{S_{XY}}{S_{XX}}\)
위에서 나오는 $S_{XY}$와 $S_{XX}$는 아래와 같이 주어진다.
\(S_{XY}= \sum (X_{i}-\overline{X})(Y_{i}-\overline{Y})\)
\(S_{XX}= \sum (X_{i}-\overline{X})^{2}\)
위에 정의된 내용으로 아래의 내용을 정리할 수 있다.
적합된 회귀식 : \(\hat{y} = \hat{\beta}_{0} + \hat{\beta}_{1}x\)
$X_{i}$에서의 적합치 : \(\hat{Y}_{i} = \hat{\beta}_{0} + \hat{\beta}_{1}X_{i}\)
i번째 잔차 : \(e_{i}=Y_{i}-\hat{Y}_{i}\)
$\sigma^{2}$의 추정치 : \(s^{2}=\frac{1}{n-2}\sum_{i=1}^{n}e^{2}_{i}\)
따라서 $\beta_{1}$의 신뢰 구간은 아래와 같다.
\[\hat{\beta}_{1} \pm t_{\alpha/2}\frac{s}{\sqrt{S_{XX}}}\]$\beta_{0}$의 신뢰 구간은 아래와 같다.
\[\hat{\beta}_{0} \pm t_{\alpha/2}s\sqrt{\frac{1}{n}+\frac{\overline{x}^{2}}{S_{XX}}}\]주어진 상수 $\beta_{10}$에 대해서 귀무가설 $H_{0} : \beta_{1}=\beta_{10}$일때 3가지 형태의 대립가설이 가능하다.
(단, \(t=\frac{\hat{\beta}_{1}-\beta_{10}}{s/\sqrt{S_{XX}}}\))
| 귀무가설 | 대립가설 | 기각역 | 비고 |
| $H_{0} : \beta_{1} = \beta _{10}$ | $H_{1} : \beta_{1} > \beta _{10}$ | $t > t_{\alpha}$ | 단측검정 |
| $H_{0} : \beta_{1} = \beta _{10}$ | $H_{1} : \beta_{1} < \beta _{10}$ | $t < -t_{\alpha}$ | 단측검정 |
| $H_{0} : \beta_{1} = \beta _{10}$ | $H_{1} : \beta_{1} \neq \beta _{10}$ | $|t| > t_{\alpha/2}$ | 양측검정 |
c. 적합도
아래와 같이 정의해보자
- $Y_{i}$ : 실제 표본의 Y값
- $\hat{Y_{i}}$ : 적합모형의 Y값
- $\overline{Y}$ : 모든 표본의 Y값 평균
- $X_{i}$ : 해당 위치에서의 X값
- $e_{i}$ : 실제값과 적합모형값의 차이, 즉 오차
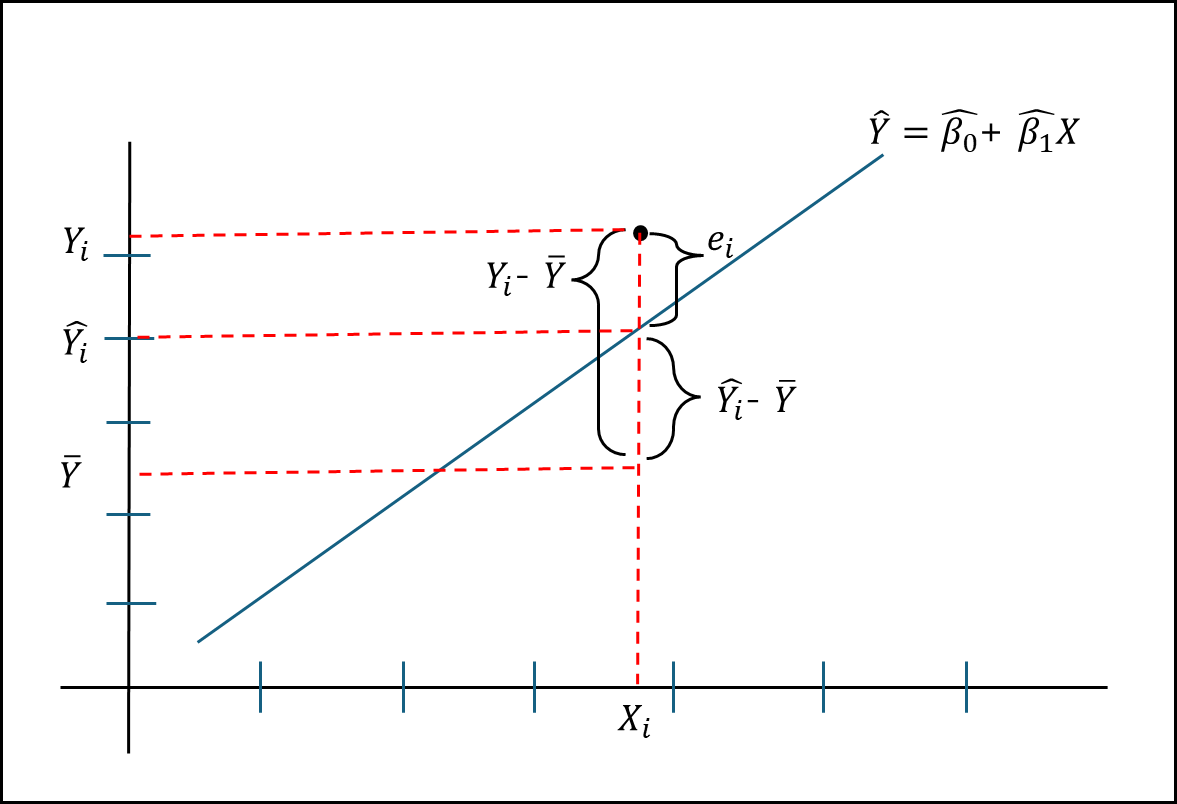
위와 같을때 총제곱합은 다음과 같다.
\[\sum (Y_{i}-\overline{Y})^{2} = \sum (\hat{Y_{i}}-\overline{Y})^{2} + \sum (Y_{i}-\hat{Y_{i}})^{2}\]식을 설명하면 아래와 같다.
SST (Total Sum of Squares, 총제곱합) = SSR (Regression Sum of Squares, 회귀제곱합) + SSE(Error Sum of Squares, 잔차제곱합)
위의 SST와 SSR, SSE를 가지고 분산분석표를 그려보면 아래와 같다.
| 요인 | 제곱합 | 자유도 | 평균제곱 | F비 |
| 회귀 | SSR | 1 | MSR=SSR/1 | $F_{0}=MSR/MSE$ |
| 오차 | SSE | n-2 | MSE=SSE(n-2) | |
| 전체 | SST | n-1 |
위의 표를 기반으로 해당 적합 모형이 얼마나 적합한지 결정 계수를 구할 수 있다.
$R^{2}=\frac{SSR}{SST}=1-\frac{SSE}{SST}$ : 결정계수(coefficient of determination)
여기서 $R^{2}$은 0과 1사이로 나타나는데 1에 가까울수록 적합하고, 0에 가까울 수록 적합하지 않다.
그리고 단순선형회귀의 경우 결정 계수는 표본상관계수의 제곱으로 나타난다.
2. 다중 선형 회귀 분석
선형 결합 형태로 나타나는 모형이다. 형태는 아래와 같다.
\[Y = \beta_{0} + \beta_{1}X_{1} + ... + \beta_{p-1}X_{p-1} +\varepsilon_{i}\]- Y : 반응변수 (Response variable), 종속변수 (Dependent variable)
- X : 공변량, 설명변수 (covariates)
- $\varepsilon$ : 오차항(Error term), 흔히 $\varepsilon \sim N(0,\sigma^{2})$이라고 가정
- $\beta_{0},\beta_{1},…,\beta_{p-1}$ : 회귀계수 (regression coefficients), 추정해야할 모수이다.
위의 식은 행렬을 이용하여 \(y=X\beta + \varepsilon\) 로 나타낼 수 있다.
이때 각 인자들의 형태는 아래와 같다.
\[y=\begin{bmatrix} Y_{1} \\ Y_{2} \\ ... \\ Y_{n} \end{bmatrix}, X = \begin{bmatrix} X'_{1} \\ X'_{2} \\ ... \\ X'_{n} \end{bmatrix} = \begin{bmatrix} 1 & X_{11} & X_{12} & ... & X_{1,p-1} \\ 1 & X_{21} & X_{22} & ... & X_{2,p-1} \\ ... & ... & ... & ... & ... \\ 1 & X_{n1} & X_{n2} & ... & X_{n,p-1} \\ \end{bmatrix} , \varepsilon = \begin{bmatrix} \varepsilon _{1} \\ \varepsilon _{2} \\ ... \\ \varepsilon _{n} \end{bmatrix}\]a. 목표
단순 선형 회귀 모델과 마찬가지로 오차제곱합인 D가 가장 작은 $\beta$값들을 찾으면 된다.
여기서 D 값을 구하는 공식은 아래와 같다.
b. 적합도
다중 회쉬에서의 분산 분석표는 아래와 같다.
| 요인 | 제곱합 | 자유도 | 평균제곱 | F비 |
| 회귀 | SSR | p-1 | MSR=SSR/(p-1) | $F_{0}=MSR/MSE$ |
| 오차 | SSE | n-p | MSE=SSE/(n-p) | |
| 전체 | SST | n-1 |