통계학 - 자료의 정리1

자료의 정리

1. 표본 평균

n개의 자료가 있고 첫번째 자료를 $x_{1}$, n번째 자료를 $x_{n}$이라 할때

\[\overline{x} = \frac{1}{n} \sum_{i=1}^{n} x_{i}\]

기하학적으로 보면 n개의 값의 무게 중심

2. 표본 중간값

n개의 자료를 작은 것으로부터 크기 순으로 나열하였을 때 가운데에 있는 값
n이 짝수일때는 중간값 두 개의 평균을 구하여 중간값으로 사용한다.

ex) 표본 배열 a = [1,2,3,4,5]일때 중간값은 3
표본 배열 b = [1,2,3,4,5,6]일때는 3과 4를 더해서 2로 나눈 3.5가 중간값

3. 표본 분위수

1) 표본 100p 백분율(Sample 100p-th percentile). 0 < p < 1

100p %개의 자료는 그 값보다 작거나 같고, 100(1-p)% 개의 자료는 그 값보다 크거나 같다.

• 25% 백분율 = 제 1 분위수 (1st quartile) = $Q_{1}$
• 50% 백분율 = 제 2 분위수 (2nd quartile) = $Q_{2}$ , 표본 중간값
• 75% 백분율 = 제 3 분위수 (3rd quartile) = $Q_{3}$

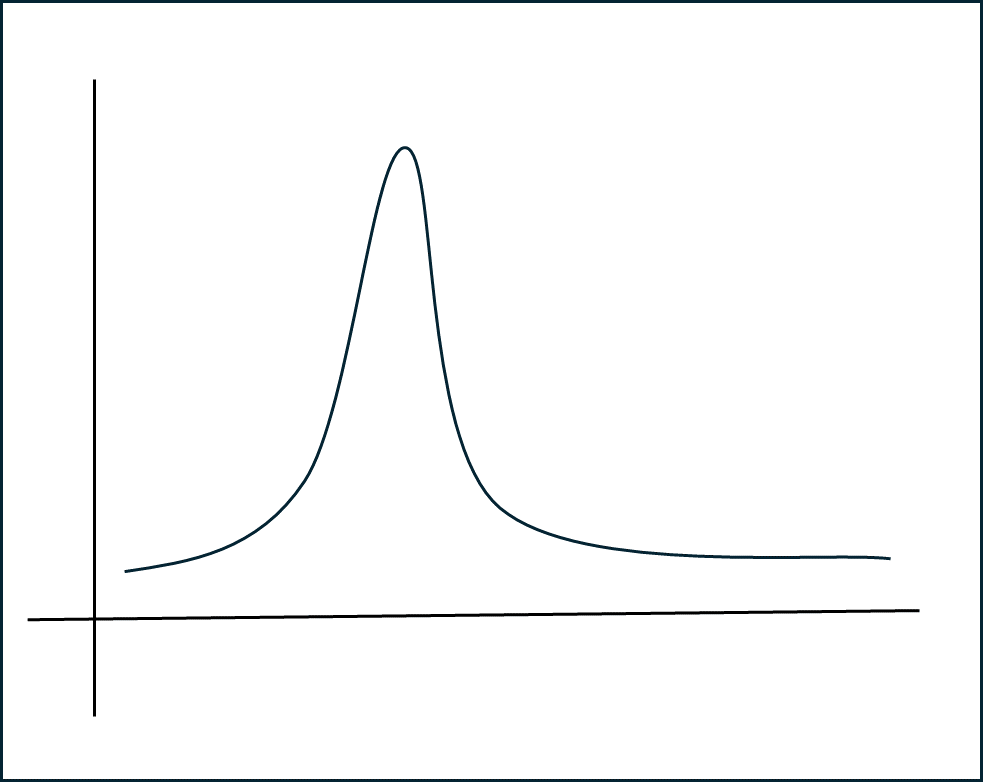
4. 분포의 형태

1) 오른쪽으로 긴 꼬리 형태

표본 평균 > 표본 중간값

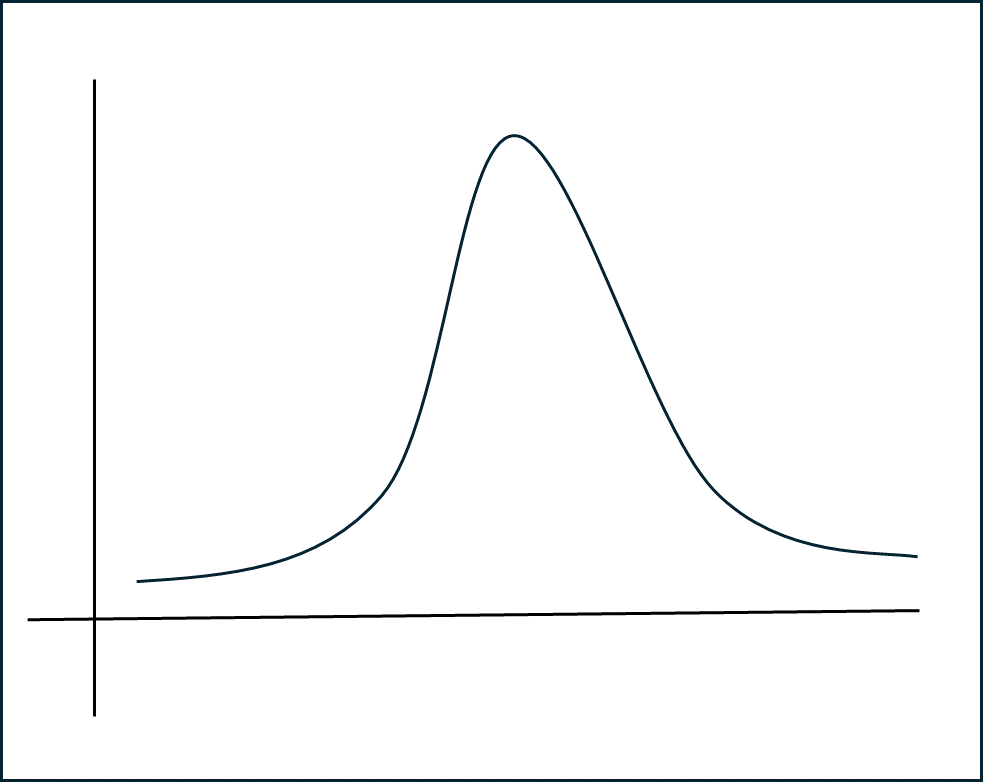
2) 대칭에 가까운 형태

표본 평균 = 표본 중간값

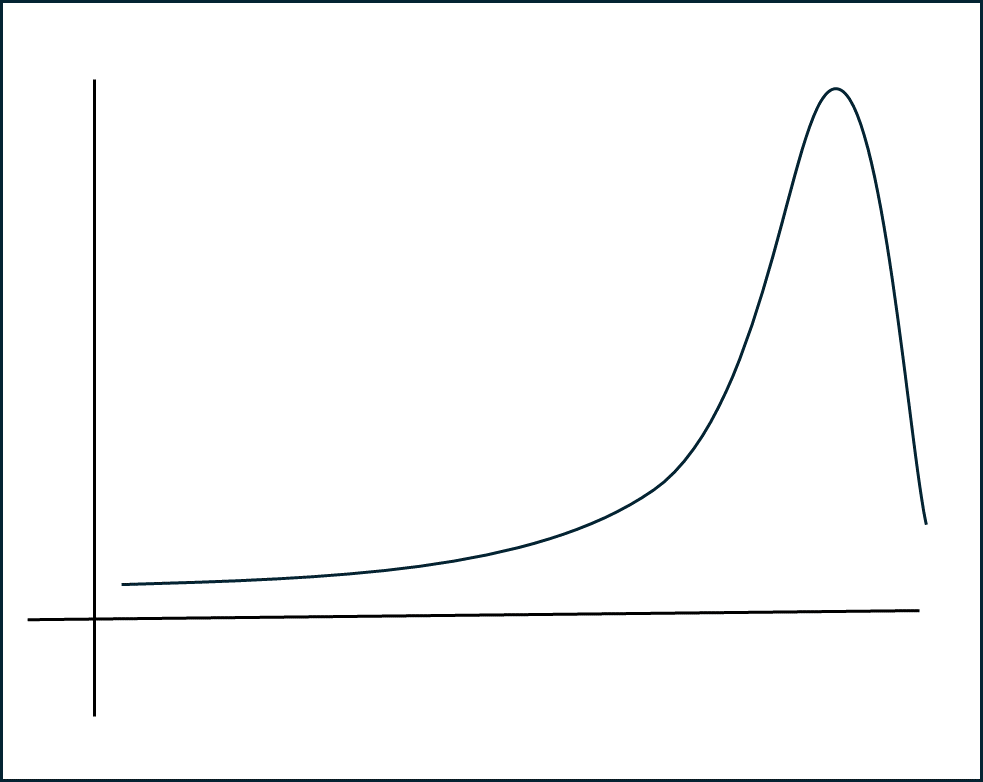
3) 왼편으로 긴 꼬리 형태

표본 평균 < 표본 중간값

5. 표본 분산

\(s^{2} = \frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}\)

6. 표본 범위

R = 최대값 - 최소값 : 표본 범위(Sample range)
IQR = $Q_{3}$ - $Q_{1}$ : 표본 사분위수 범위(Sample Interquartile range)

7. 상자 그림

연속성 변수에 대한 데이터의 분포를 보여준다.


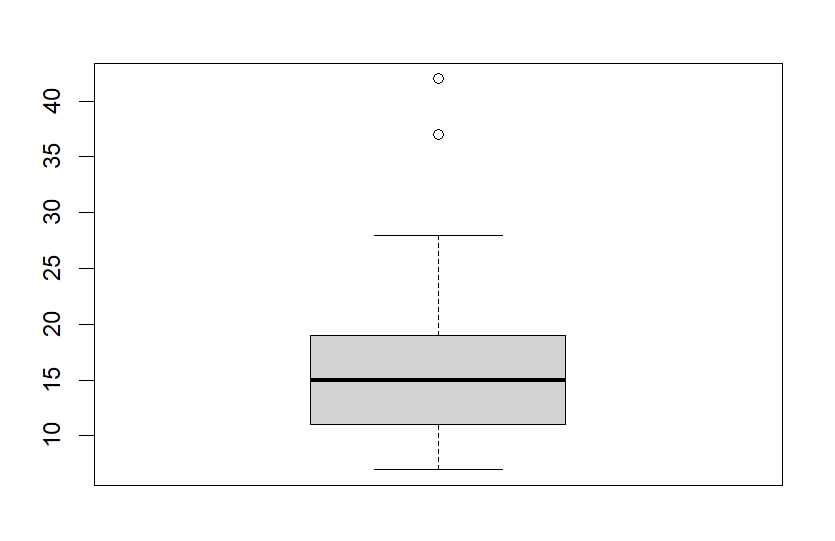
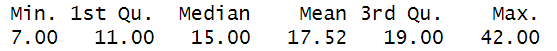
상자 안 중심선은 데이터의 중앙값을 나타내며, 데이터가 대칭이면 중앙값이 상자 중앙에 위치한다. 데이터의 편중 위치에 따라 상자의 위쪽이나 아래쪽으로 중심선이 이동한다.
상자의 맨 아래와 맨위는 1분위수와 3분위수를 표현한 것이다.

참고자료

• R을 이용한 통계학 개론