GPU 프로그래밍 - 행렬 곱셈
Matrix multiplication 예제분석
2차원 행렬 곱셈에 대한 GPU를 이용한 계산이다.
처음 2개의 함수는 HOST 즉 CPU를 이용한 함수이고, 뒤에 gpu~ 함수들은 모두 CUDA 코어를 사용한 함수이며 Tensor 코어를 사용한 계산은 이후에 포스팅할 예정이다.
1. hostmult0 예제 분석
1
2
3
4
5
6
7
8
9
10
int hostmult0(float* C, float* A, float* B, int Ay, int Ax, int Bx) {
// compute C = A * B for matrices (assume Ax = By and C is Ay x Bx)
for (int i = 0; i < Ay; i++)
for (int j = 0; j < Bx; j++) {
C[i * Bx + j] = 0.0f; // Cij = ∑k Aik * Bkj
for (int k = 0; k < Ax; k++)
C[i * Bx + j] += A[i * Ax + k] * B[k * Bx + j];
}
return 0;
}
cpu에서 구동되는 A와 B의 배열을 곱한 값을 C배열에 저장하는 코드이다.
사전에 할당해둔 C배열은 가장 안쪽 루프가 돌기전 0으로 초기화 된 후 가장 안쪽 루프가 돌면서 계산되는 값이 더해진다.
위 경우에 컴파일러가 별다른 최적화를 하지 않는다고 한다면, C[i * Bx + j] = 0.0f;에서 Write 한번 C[i * Bx + j] += A[i * Ax + k] * B[k * Bx + j]; 에서 READ 3번에 WRITE 1번으로 총 READ 3번 WRITE 2번이 일어난다.
2. hostmult1 예제 분석
1
2
3
4
5
6
7
8
9
10
int hostmult1(float* __restrict C, float * __restrict A, float* __restrict B, int Ay, int Ax, int Bx) {
// compute C = A * B for matrices (assume Ax = By and C is Ay x Bx)
for (int i = 0; i < Ay; i++)
for (int j = 0; j < Bx; j++) {
C[i * Bx + j] = 0.0f; // Cij = ∑k Aik * Bkj
for (int k = 0; k < Ax; k++)
C[i * Bx + j] += A[i * Ax + k] * B[k * Bx + j];
}
return 0;
}
hostmult0와 코드 자체는 동일하고 __restrict 전처리 지시자만 붙은 형태이다. 이 __restrict 전처리 지시자는 컴파일러에게 알려주는 것인데, 해당 포인터를 다른 포인터가 가르키는 일은 없다고 명시적으로 알려주는 것이다.
이렇게 미리 알려주는 경우 아래와 같은 코드로 해석될 수 있다.
1
2
3
4
5
6
7
8
9
10
11
int hostmult1_opt(float* __restrict C, float* __restrict A, float* __restrict B, int Ay, int Ax, int Bx) {
// compute C = A * B for matrices (assume Ax = By and C is Ay x Bx)
for (int i = 0; i < Ay; i++)
for (int j = 0; j < Bx; j++) {
float tmp = 0.0f; // Cij = ∑k Aik * Bkj
for (int k = 0; k < Ax; k++)
tmp += A[i * Ax + k] * B[k * Bx + j];
C[i * Bx + j] = tmp;
}
return 0;
}
위 코드에서 tmp 변수를 선언하고 0으로 초기화시켜 임시 버퍼로 사용한다.
이 경우 컴파일러에서 어셈블리어로 변경할 때 위 tmp 값은 register에서 담고 있도록 변환하게 되는데 레지스터는 매우 빠른 저장장치이기 때문에 성능이 올라간다.
이후 CPU로 행렬 계산시 높은 성능을 뽑아내기 위한 코드는 이곳 포스팅을 참조하기 바란다.
3. gpumult0 ~ 1 예제 분석
1
2
3
4
5
6
7
8
9
__global__ void gpumult0(float* C, const float* A, const float* B, int Ay, int Ax, int Bx) {
int tx = blockIdx.x * blockDim.x + threadIdx.x;
int ty = blockIdx.y * blockDim.y + threadIdx.y;
if (ty >= Ay || tx >= Bx) return;
C[ty * Bx + tx] = 0.0f;
for (int k = 0; k < Ax; k++)
C[ty * Bx + tx] += A[ty * Ax + k] * B[k * Bx + tx];
}
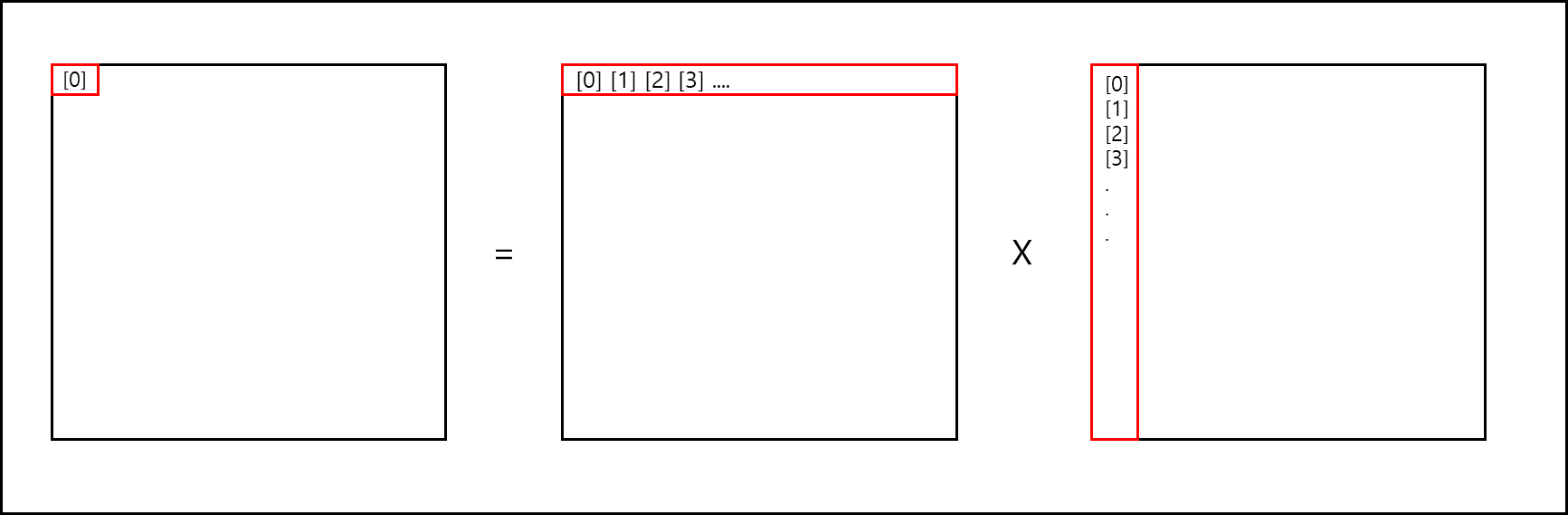
위 코드는 전체 행렬 값의 각 한 원소마다 한 개의 스레드를 배정하여 C 배열의 해당 위치를 0으로 초기화하고 계산하여 C에 부분합 하는 형태로 구현된 것이다.
그림으로 나타내면 아래와 같다.
C[0][0] = 0;
C[0][0] += (A[0][0]B[0][0]);
C[0][0] += (A[0][1]B[1][0]);
C[0][0] += (A[0][2]B[2][0]);
C[0][0] += (A[0][3]B[3][0]);
… …
C[0][0] += (A[0][Width-1]*B[Height-1][0]);
이는 CPU로 행렬 계산하는 것과 크게 다르지 않은 방식이다.
만약 좀 더 효율적으로 하고 싶다면 아래의 코드로 변경할 수도 있다.
1
2
3
4
5
6
7
8
9
10
__global__ void gpumult0(float* C, const float* A, const float* B, int Ay, int Ax, int Bx) {
int tx = blockIdx.x * blockDim.x + threadIdx.x;
int ty = blockIdx.y * blockDim.y + threadIdx.y;
if (ty >= Ay || tx >= Bx) return;
float csum = 0.0f;
for (int k = 0; k < Ax; k++)
csum += A[ty * Ax + k] * B[k * Bx + tx];
C[ty * Bx + tx] = csum;
}
위 코드는 register에 부분합을 다 더해두고 최종적으로 메모리에다가 넣는 방식으로 global_memory access 횟수를 줄일 수 있다는 점에서 효율적이다. 위의 코드 역시 원래 코드에서 __restrict를 붙이면 컴파일러가 동일하게 최적화해주는 것 같다.
4. gputiled 예제 분석
GPU 구동 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
template <int TS> __global__ void gputiled(float* __restrict C, float * __restrict A, float * __restrict B,
int Ay, int Ax, int Bx) {
__shared__ float Atile[TS][TS]; // tile in A eg [16][16]
__shared__ float Btile[TS][TS]; // tile in B eg [16][16]
int tx = threadIdx.x; // tile col index j
int ty = threadIdx.y; // tile row index i
int ocx = blockDim.x * blockIdx.x; // tile x origin in C (all threads)
int ocy = blockDim.y * blockIdx.y; // tile y origin in C (all threads)
int ax = tx; // j or x in first tile on A
int ay = ocy + ty; // i or y in first tile on A and C
int bx = ocx + tx; // j or x in first tile on B and C
int by = ty; // i or y in first tile on B
float csum = 0.0f;
for (int t = 0; t < Ax / TS; t++) {
Atile[ty][tx] = A[ay * Ax + ax]; // copy A tile to shared mem
Btile[ty][tx] = B[by * Bx + bx]; // copy B tile to shared mem
__syncthreads();
for (int k = 0; k < TS; k++) csum += Atile[ty][k] * Btile[k][tx];
__syncthreads();
ax += TS; // step A tiles along rows of A
by += TS; // step B tiles down cols of B
}
C[ay * Bx + bx] = csum; // store complete result
}
Host 구동 코드
1
2
3
4
5
6
7
8
//...
if (tilex == 8)
gputiled<8> << < blocks, threads >> > (d_C, d_A, d_B, Arow, Acol, Bcol);
else if (tilex == 16)
gputiled<16> << <blocks, threads >> > (d_C, d_A, d_B, Arow, Acol, Bcol);
else if (tilex == 32)
gputiled<32> << <blocks, threads >> > (d_C, d_A, d_B, Arow, Acol, Bcol);
//...
c++ 문법인 template으로 짜여있는 gputiled 함수는 타일 크기를 입력 받아서 구동되며 int 값으로 지정되는데 host 구동 코드를 살펴보면 8, 16, 32로 나뉘어서 구동된다.
입력 받은 크기 만큼 A와 B 행렬에 대해서 tile 크기를 잡고 이는 shared memory에 할당된다. 그리고 tile 크기만큼 메모리의 행렬에서 복사해온뒤에 각 값을 계산해서 임시 변수(레지스터에 할당되는)에 넣고 최종적으로 Global memory에 위치한 C행렬에 기재된다.
전체 코드의 흐름은 앞선 값들과 비슷하나 shared memory를 사용해서 성능을 올렸다는 점이 가장 크게 다르다.
여기서 아래와 같이 loop unrolling을 적용하면 좀 더 최적화 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
template <int TS> __global__ void gputiled1(float* __restrict C, float* __restrict A, float* __restrict B,
int Ay, int Ax, int Bx) {
__shared__ float Atile[TS][TS]; // tile in A eg [16][16]
__shared__ float Btile[TS][TS]; // tile in B eg [16][16]
int tx = threadIdx.x; // tile col index j
int ty = threadIdx.y; // tile row index i
int ocx = blockDim.x * blockIdx.x; // tile x origin in C (all threads)
int ocy = blockDim.y * blockIdx.y; // tile y origin in C (all threads)
int ax = tx; // j or x in first tile on A
int ay = ocy + ty; // i or y in first tile on A and C
int bx = ocx + tx; // j or x in first tile on B and C
int by = ty; // i or y in first tile on B
float csum = 0.0f;
#pragma unroll 3 // Line A
for (int t = 0; t < Ax / TS; t++) {
Atile[ty][tx] = A[ay * Ax + ax]; // copy A tile to shared mem
Btile[ty][tx] = B[by * Bx + bx]; // copy B tile to shared mem
__syncthreads();
#pragma unroll // Line B
for (int k = 0; k < TS; k++)
csum += Atile[ty][k] * Btile[k][tx];
__syncthreads();
ax += TS; // step A tiles along rows of A
by += TS; // step B tiles down cols of B
}
C[ay * Bx + bx] = csum; // store complete result
}
loop unrolling에서 대해서 잘 모른다면 이곳 을 참고하면 된다.
#pragma unroll N 코드는 실질적으로 컴파일러에서 처리하는 전처리 지시문이며, 만약에 Line B에서 N이 3이라면 바로 아래의 for문을 아래와 같이 바꿔주는 역할을 한다.
1
2
3
4
5
6
7
8
//...
int k = 0;
for ( ; k + 3 < M; k += 3) {
csum += Atile[ty][k] * Btile[k][tx];
csum += Atile[ty][k+1] * Btile[k+1][tx];
csum += Atile[ty][k+2] * Btile[k+2][tx];
}
//...
만약 이 N값이 정해져있다면 정해진 값대로 풀어주고, 아니라면 최대값으로 해준다.
확실하지는 않지만 이 최대값이란 것은 각 GPU에 맞는 값이 별도로 지정되어있는 것 같다.
(실제로 CPU에서는 최적화할때 어디까지 Unroll하면 좋은지가 메뉴얼에 포함되어있다고 한다)ㄴ
사실 실질적으로 해당 코드는 의미가 없는게 nvcc 컴파일러가 기본적으로 unroll을 이용한 최적화를 하기 때문에 실질적으로 unroll한것과 하지 않은 것의 성능 차이가 나지 않는다.
5. gputiled_more_work 예제 분석
GPU 구동 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
template <int TS, int WPT, int RTS> __global__ void gputiled(float* __restrict C, float * __restrict A,
float * __restrict B, int Ay, int Ax, int Bx) {
__shared__ float Atile[TS][TS]; // tile in A eg [16][16]
__shared__ float Btile[TS][TS]; // tile in B eg [16][16]
float accum[WPT];
for (int w = 0; w < WPT; w++) accum[w] = 0.0f;
int tx = threadIdx.x; // tile col index j
int ty = threadIdx.y; // tile row index i
int ocx = blockDim.x * blockIdx.x; // tile x origin in C (all threads)
int ocy = WPT * (blockDim.y * blockIdx.y); // tile y origin in C (all threads)
int ax = tx; // j or x in first tile on A
int ay = ocy + ty; // i or y in first tile on A and C
int bx = ocx + tx; // j or x in first tile on B and C
int by = ty; // i or y in first tile on B
for (int t = 0; t < Ax / TS; t++) {
for (int w = 0; w < WPT; w++) {
Atile[ty + w * RTS][tx] = A[(ay + w * RTS) * Ax + ax]; // copy A tile to shared mem
Btile[ty + w * RTS][tx] = B[(by + w * RTS) * Bx + bx]; // copy B tile to shared mem
}
__syncthreads();
for (int k = 0; k < TS; k++) {
float tmp = Btile[k][tx];
for (int w = 0; w < WPT; w++)
accum[w] += Atile[ty + w * RTS][k] * tmp;
}
__syncthreads();
ax += TS; // step A tiles along rows of A
by += TS; // step B tiles down cols of B
}
for (int w = 0; w < WPT; w++)
C[(ay + w * RTS) * Bx + bx] = accum[w]; // store complete result
}
Host 구동 코드
1
2
3
4
5
6
7
8
9
10
11
12
//...
#define WPT_NUM 8
//...
if (tilex == 16)
gputiled<16, WPT_NUM, 16 / WPT_NUM> << <blocks, threads >> > (d_C, d_A, d_B, Arow, Acol, Bcol);
else if (tilex == 32)
gputiled<32, WPT_NUM, 32 / WPT_NUM> << <blocks, threads >> > (d_C, d_A, d_B, Arow, Acol, Bcol);
//...
gputiled 함수가 각 Thread당 한 개의 원소 계산을 했다면 이 코드는 Thread당 다수의 원소 계산을 시키는 코드이다.
Work per thread의 의미로 WPT이고, 위 코드 기준으로 Thread당 8개의 원소 값을 계산하게 된다.
※ 내용 업데이트 및 추가적인 검증 예정
참고문헌
- 서강대학교 임인성 교수님 - 기초 GPU 프로그래밍 수업 자료
- NVIDIA - NVIDIA ADA GPU ARCHITECTURE